Реферат: Решение обратных задач теплопроводности для элементов конструкций простой геометрической формы

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДНЕПРОПЕТРОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

КАФЕДРА ПГД И ТМО

НА ТЕМУ: «РЕШЕНИЕ ОБРАТНЫХ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ ДЛЯ

ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ПРОСТОЙ ГЕОМЕТРИЧЕСКО ФОРМЫ»

ВЫПОЛНИЛА: СТ. ГР. МТ-98-1

ДАЦЕНКО И. Н.

ДНЕПРОПЕТРОВСК

-2001-

Постановки задач о теплообмене между твердым телом или некоторой системой и окружающей средой рассматриваются с точки зрения соотношений причина—следствие. При этом к причинным характеристикам теплообменного процесса в теле (системе) в соответствии с принятой моделью отнесем граничные условия и их параметры, начальные условия, теплофизические свойства, внутренние источники тепла и проводимости, а также геометрические характеристики тела или системы. Тогда следствием будет то или иное тепловое состояние, определяемое температурным полем исследуемого объекта.

Установление причинно - следственных связей составляет цель прямых задач теплообмена. Наоборот, если по определенной информации о температурном поле требуется восстановить причинные характеристики, то имеем ту или иную постановку обратной задачи теплообмена.

Постановки обратных задач, в отличие от прямых, не соответствуют физически реализуемым событиям. Например, нельзя обратить ход теплообменного процесса и тем более изменить течение времени. Таким образом, можно говорить о физической некорректности постановки обратной задачи. Естественно, что при математической формализации она проявляется уже как математическая некорректность (чаще всего неустойчивость решения) и обратные задачи представляют собой типичный пример некорректно поставленных задач в теории теплообмена.

Граничная ОЗТ — восстановление тепловых условий на границе тела. К этому типу задач отнесем также задачу, связанную с продолжением решения уравнения теплопроводности от некоторой границы, где одновременно заданы температура Т( х*, т) и плотность теплового потока q( х*, т);

Организация охлаждения конструкции камер сгорания является одним из важнейших вопросов проектирования и по сравнению с другими типами тепловых машин усложняется тем, что тепловые процессы протекают при высоких температурах К и давлениях. Так как высокотемпературные продукты сгорания движутся по камере с очень большой скоростью, то резко возрастают коэффициент конвективной теплоотдачи от горячих продуктов сгорания к стенкам камеры и конвективные тепловые потоки , доходящие в критическом сечении сопла до 23,26 - 69,78. Кроме того, теплообмен в конструкции характеризуется высоким уровнем радиации в камере, что приводит к большим лучистым тепловым потокам /13/.

Вследствие мощных суммарных конвективных и лучистых тепловых потоков в стенке камеры температура ее может достигать значений превышающих (1000 - 1500С. Величина этих потоков определяется значениями режимных параметров, составом продуктов сгорания в ядре газового потока и в пристеночном слое, а также температурой внутренней поверхности конструкции. Из-за изменения диаметра проточной части по длине теплопровод от продуктов сгорания оказывается неравномерным. Неравномерным является также распределение температуры по периметру, обусловленное изменением состава продуктов сгорания.

Коэффициент теплоотдачи от продуктов сгорания определяется с учетом совместного воздействия конвективного и лучистого теплового потоков в соответствующем сечении конструкции узла по значениям параметров (давление, состав и температура продуктов сгорания в ядре газового потока и в пристеночном слое) на установившемся режиме эксплуатации /13/.

Время выхода рассматриваемых конструкций на установившийся тепловой режим соизмеримо и может оказаться даже большим времени их работы при эксплуатации. В этих условиях задача определения теплового состояния в период работы сводится к расчету прогрева их под воздействием высокотемпературных продуктов сгорания /1, 2/.

Рассмотрим следующую схему корпуса камеры сгорания.

На поверхности в сечении располагается по две точки замера, расположенных в диаметрально противоположных точках периметра корпуса.

В сечении I - I корпуса сопла можно представить в виде однослойной неограниченной пластины, двухслойной - сечение II - II (Рис.1).

Расчетные схемы элементов конструкции представлены на рисунке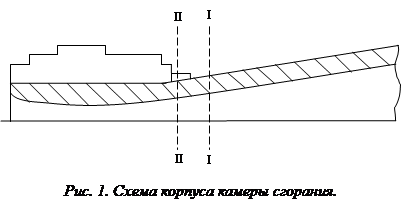 2 и 3.

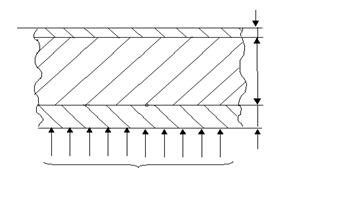Обратная тепловая задача для пластины формулируется следующим образом. Требуется по замерам температуры и теплового потока к пластине (рис.2) при X = 0 найти изменения температуры и теплового потока на поверхности X = 1.

Решение обратной тепловой задачи в такой постановке целесообразно построить с использованием решения задачи Коши /3/.

В пространстве переменных задана некоторая гладкая поверхность Г. С каждой точкой связывается некоторое направление , некасательное Г.

В окрестности поверхности Г требуется найти решение уравнения.

удовлетворяющего условиям Коши

где - безразмерные время и координата.

Нетрудно убедиться, что решение задачи (1), (2), записанное в виде:

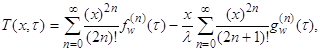(3)

и является искомым /10/.

Утверждения о существовании решения (3), об аналитичности этого решения и его единственности в классе аналитических функций составляют содержание известной классической теоремы Коши - Ковалевской /11/.

Решение (13) при заданных и позволяет найти искомые изменения температуры и теплового потока Однако в такой интерпретации решения (3), где функции известны из эксперимента с некоторой заданной погрешностью, необходимо учитывать и тот факт, что вычисление операторов дифференцирования неустойчиво к возмущениям в исходных данных /12/.

Таким образом, имеем типичную некорректную задачу, для построения устойчивого решения которой необходимо построение регуляризирующих алгоритмов.

Сохраним в решении (3) конечное число слагаемых N. Введем обозначения

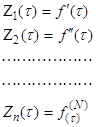(4)

Интегрируя (4) получим систему интегральных уравнений Вольтерра первого рода:

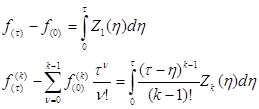, (5)

где k =1, 2, ... , N.

Соотношения для теплового потока в (3) записывается аналогично. В дальнейшем будем считать, что на поверхности X = 0 теплосъем отсутствует, то есть стенка теплоизолирована. Тогда решение (3) с учетом обозначений (4) записывается в виде

(6)

Таким образом, граничные условия при X = 1 восстанавливаются соотношением (6), в котором функции находятся из решения интегральных уравнений (5)

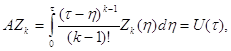(7)

где правая часть задается приближенно, то есть

Здесь - числовой параметр, характеризующий погрешность правой части уравнения (7).

Задача (7) является, в общем случаи некорректно поставленной /12/. Наиболее распространенным в настоящее время эффективным регуляризующим алгоритмом для ее решения является алгоритм, основанный на минимизации функционала А.Н.Тихонова /12/.

(8)

С последующим выбором параметра регуляризации по так называемому принципу невязки.

Например, если - какая - либо экстремаль функционала (8), реализующая его глобальный минимум при заданном и фиксированном , то числовой параметр определяется из условия

(9)

Регуляризующий алгоритм (7) - (9) подробно изучен в /12/ и обладает устойчивостью к малым возмущениям правой части (7).

Правая часть уравнения (7) при решении формировалась следующим образом. Функция характеризующая изменение температуры поверхности, задавалась таблицей. Начальные условия для 1, 2, … , N-1) находились из соотношения /3/:

(10)

где , - распределение температуры, заданное в начальный момент времени. Откуда для равномерного распределения температуры в начальный момент времени имеет

1, 2, … , N-1 (11)

Из анализа теплофизических и геометрических характеристик конструкции камеры сгорания следует возможность представления системы пластин теплового отношения (рис.1) в виде пластины из теплозащитного покрытия и оболочки, которую можно рассматривать как тепловую емкость. Это дает возможность воспользоваться для построения решения обратной тепловой задачи для заданного узла решением задачи Коши (3). В системе координат, представленной на Рис.1, поверхность при X = 0 будем считать теплоизолированной, то есть

(12)

Кроме этого предположим, система пластин в начальный момент времени прогрета равномерно и, следовательно, начальные условия для функции имеют вид (11).

При сделанных выше предположениях условия Коши (12) для этой задачи имеют вид

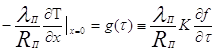(13)

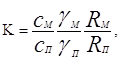Где

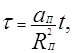
Подставляя значение из условия (2) в решение задачи Коши (3) получим

(14)

где

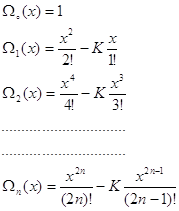
Таким образом, решение этой задачи имеет вид

(15)

где нам задана, а функции (n=1, 2, … , N) определяются из решения интегральных уравнений Вольтерра первого рода (5) методом регуляризации

(7) - (9).

Следовательно, искомые величины определяются из решения (4) с использованием регуляризирующего алгоритма (7) - (9).

Метод наименьших квадратов.

Пусть функция задана на своими значениями в точках . Рассмотрим совокупность функций

(16)

линейно независимых на .

Будем отыскивать линейную комбинацию этих функций

(17)

так, чтобы сумма квадратов ее отклонений от заданных значений функции в узлах имела бы наименьшее возможное значение, то есть величина

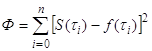(18)

принимала бы минимальное значение.

Заметим, что упомянутая сумма является функцией коэффициентов

. (19)

Поэтому для решения нашей задачи воспользуемся известным приемом дифференциального исчисления, а именно: найдем частные производные функции по всем переменным и приравняем их нулю:

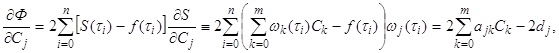
где

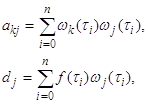
Отсюда видим, что метод наименьших квадратов приводит к необходимости решать систему алгебраических уравнений

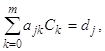
. (20)

Можно доказать, что если среди точек нет совпадающих и , то определитель системы (20) отличен от нуля и, следовательно, эта система имеет единственное решение (19). Подставив его в (17), найдем искомый обобщенный многочлен , те есть многочлен, обладающий минимальным квадратичным отклонением . Заметим, что при m = n коэффициенты (19) можно определить из условий причем в этом случае Ф = 0. Следовательно, мы приходим здесь к рассмотренной ранее задаче интерполирования.

Функции , , как известно, образуют систему Чебушева на любом сегменте и могут быть использованы для практической реализации описанного метода.

Легко видеть, что коэффициенты и свободные члены системы (20) в этом случае представим как

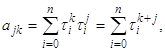(21)

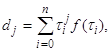
(22)

Заметим здесь, что матрица является симметричной и положительно определенной, так как квадратичная форма 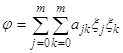неотрицательна для любых значений переменных причем только при Действительно,

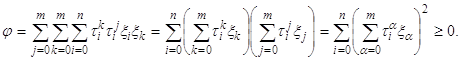
Пусть задана система алгебраических уравнений

(23)

где - невырожденная квадратная матрица m – го порядка, а и - вектор – столбцы, согласованные в размерностью матрицы А.

Выделяют два класса методов решения таких систем: прямые и итерационные.

Прямые методы основаны на разложении матрицы А в произведении более простых матриц (диагональных, треугольных, ортогональных). В этом случае исходная система уравнений (23) распадается на несколько более простых систем, решаемых последовательно. Если при этом все вычисления производить без округлений, то через вполне определенное заранее известное конечное число шагов получится точное решение системы (23).

Поэтому их называют также точными. Альтернативой для указанных методов являются итерационные алгоритмы, в которых решение находится как предел при последовательных приближений , где - номер итераций.

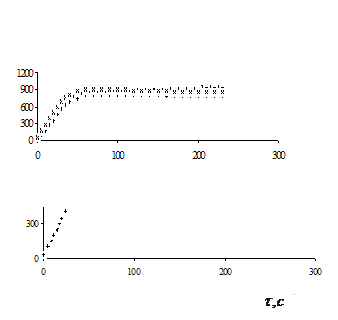
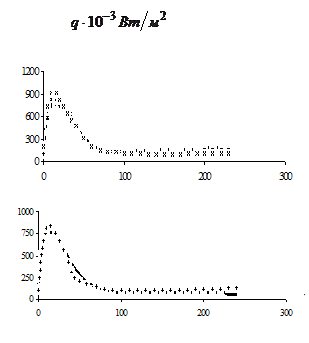
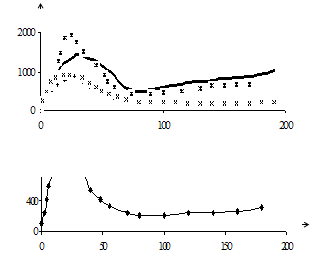
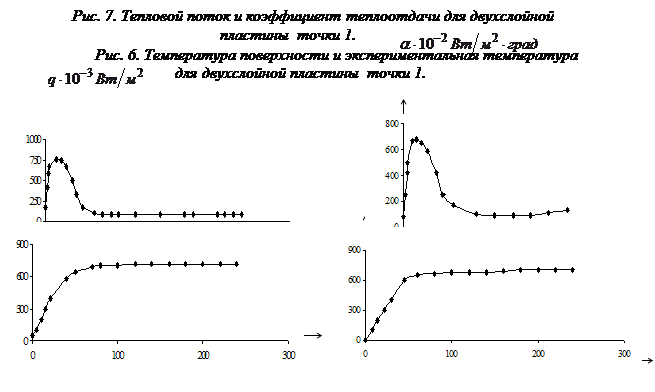
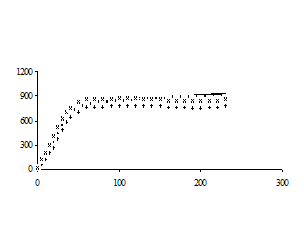Зависимости температуры поверхности и экспериментальной температуры от времени, а также теплового потока и коэффициента теплоотдачи представлены на рисунках 4, 5, 6 ,7 и 8 соответственно.

Т, К

Рис. 8. Температура поверхности и экспериментальная температура

для двухслойной пластины точки 2.

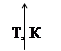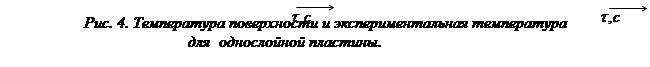В реальных условиях измеряемые температуры (то есть исходные данные для обратной тепловой задачи) являются случайными величинами из-за дефектов производства, технологии изготовления, загрязнения поверхности, погрешности измерения и обработки экспериментальной информации. Влияние погрешностей исходной информации на решение обратной задачи теплопроводности оценивалось с помощью метода статистических испытаний Монте – Карло / 5-8 /. Анализ результата статистического моделирования решения обратной задачи позволяет установить коридор ошибок искомых граничных условий.

Одним из методов решения ОЗТ является метод статистических испытаний Монте –Карло, который заключается в статистическом моделировании аналитических решений ОЗТ с учетом случайного характера исходных данных /121/.

В методе Монте-Карло основным является случайная выборка исходных данных /24/. В данной работе для этого необходим источник случайных чисел.

Введем для исходных данных обозначение

(24)

где - математическое ожидание j – го параметра в точках. Ошибку представим в виде

= (25)

где - максимально возможная погрешность,

- функция возмущения, в общем случае различная во всех точках.

Функция возмущения имеет вид при возмущении по нормальному закону распределения плотностей вероятностей при использовании правила "трех сигм"; - случайная величина, распределенная по нормальному закону с математическим ожиданием m = 0 и дисперсией Д = 1.

Используя метод Монте – Карло можно исследовать влияние погрешности исходной информации (геометрические размеры, место установки температурного датчика, теплофизические характеристики, измерения и обработки экспериментальной температуры внутренних точек тела) на решение ОЗТ. Коридор ошибок восстановленного решения можно определить по результатам статистической обработки полученных реализации. Кроме того, процедура Монте – Карло позволяет рассматривать влияние каждой входной величины на решение ОЗТ. Найденные таким путем статистические характеристики решения ОЗТ можно использовать для того, чтобы направить инженерные усилия на уменьшение именно тех случайных вариаций, которые наиболее сильно сказываются на решении ОЗТ.

Проведенные расчеты для однослойной пластины показали, что погрешность в задании экспериментальной температуры до 5% вызывает максимальные отклонения температуры поверхности до 10% на временном интервале 0 - 55 сек, а на остальном временном участке до 5%.

Максимальные отклонения теплового потока на тех же временных интервалах составляют соотственно 20% и 10%.

Проведенные расчеты для двухслойной пластины показали, что погрешность в задании экспериментальной температуры до 5% вызывает максимальные отклонения температуры до 10% на временном интервале 0 - 50 сек, а на остальном временном участке до 5%. Максимальные отклонения теплового потока на тех же временных интервалах составляют соответственно 20% и 10%.

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА

1. Алифанов О.В. Обратные задачи теплообмена. – М: Машиностроение, 1988. – 280 с.

2. Алифанов О.В., Артюхин Е.А., Румянцев С.Я. Экспериментальные методы решения некорректных задач. – М.: Наука, 1988. – 288 с.

3. Веселовский В.Б., Лазученков Н.М, Швачич С.В. Обработка и интерпретация результатов нестационарных экспериментов при исследовании процессов тепло – и массообмена // Прикладные вопросы аэродинамики летательных аппаратов. Киев: Наук. думка, 1984. – С. 138 – 140.

4. Веселовский В.Б. Решение задач нестационарной теплопроводности для многослойных теплозащитных покрытий // Прикладные вопросы аэродинамики. – Киев: Наук. думка, 1987. – с. 95 – 100.

5. Веселовский В. Б. Нелинейные задачи теплопроводности для составных элементов конструкций // Прикладные задачи гидродинамики и тепломассообмена в энергетических установках. – Киев: Наук. думка, 1989. – С. 113 – 117.

6. Веселовский В.Б. Нестационарное температурное поле составных элементов конструкций // Математические методы тепломассопереноса. – Днепропетровск: ДГУ, 1986, с. 107 –110.

7. Веселовский В.Б. Решение прямых задач теплопроводности для многослойных пластин и построение алгоритмов восстановления граничных условий // Тезисы докладов 2 - ой Республиканского симпозиума по дифференциальным и интегральным уравнениям. – Одесса: Одесский ун – т, 1978. – с. 43 – 44.

8. Веселовский В.Б. Тепловы режимы составных элементов конструкции летательных аппаратов // Тепломассообмен – ММФ – Минск: ИТМО АНБ, 1996, - том IX (Вычислительный эксперимент в задачах тепломассообмена и теплопередачи).

С. 37 – 41.

9. Коваленко Н.Д., Шмукин А.А., Гужва М.И., Махин В.В. Нестационарные тепловые процессы в энергетических установках летательных аппаратов. – Киев: Наук. думка, 1988. – 224 с.