Реферат: I must do my duty
(continue)
I.G. Goriachko, St. Petersburg, in February, 23.
Forms of neutral and changed body’s
trajectories in Nature are very differently and depended on a
pressure (p) and temperature (T) of surroundings. With reference to
microcosm, the neutral
bodies (photons,
roentgen-rays, gamma-rays, free neutrons, and etc.) for lack of
influence to them coulomb’s forces always moving merely by the
parabolical
trajectories. The changed
orbital bodies
(electrons, protons,
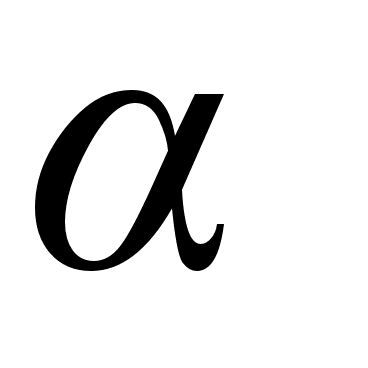 -particles,
and etc., being on the steady atom’s and nucleus’s
orbits) always moving merely by elliptical
orbits. These changed
particles by their
crossing
from the one to the next steady elliptical
orbit (and a free changed ones) always moving merely by hyperbolical
trajectories. As a result of these crossings eccentricities of
trajectories suddenly changed from the range
-particles,
and etc., being on the steady atom’s and nucleus’s
orbits) always moving merely by elliptical
orbits. These changed
particles by their
crossing
from the one to the next steady elliptical
orbit (and a free changed ones) always moving merely by hyperbolical
trajectories. As a result of these crossings eccentricities of
trajectories suddenly changed from the range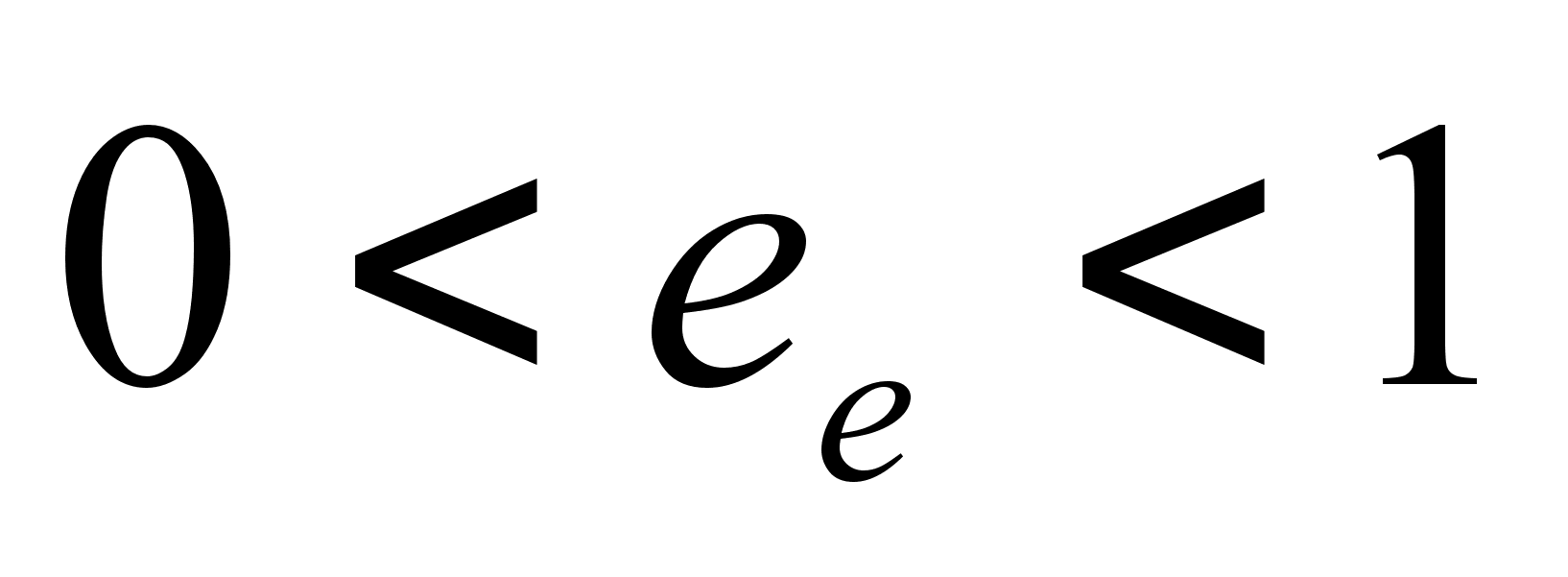 to
the
to
the
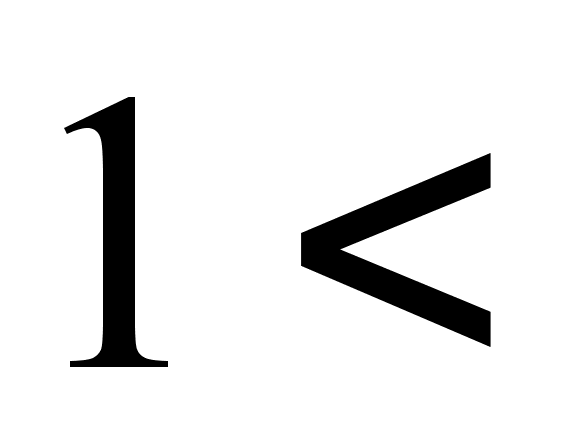
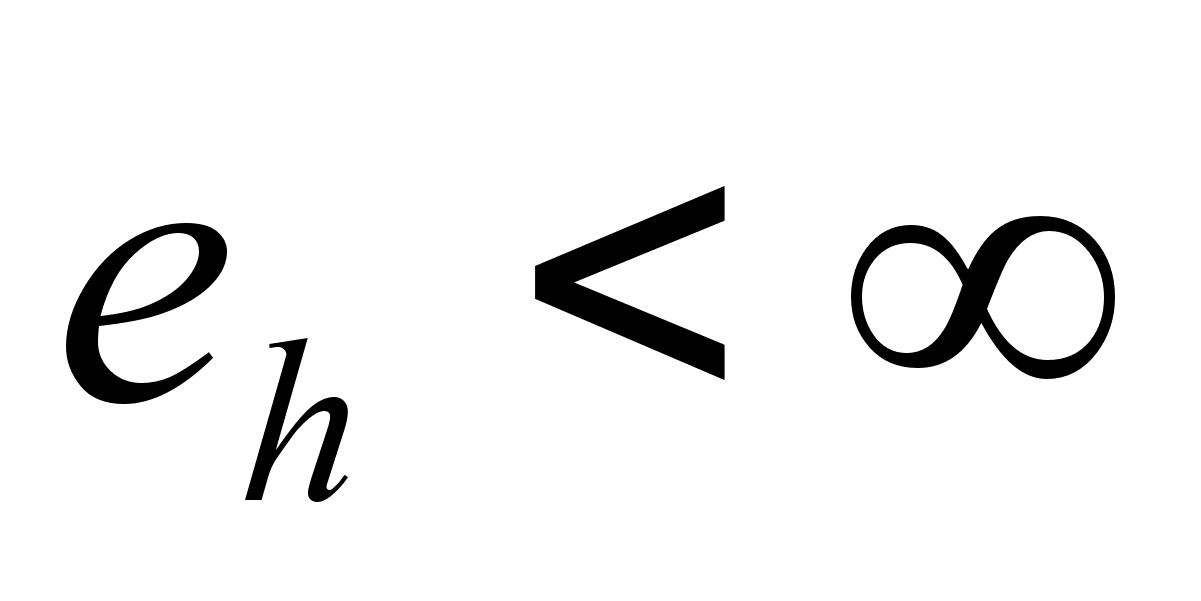 (and back). This signified that eccentricity (e) of the orbit is
appeared as the quantum
parameter depended
on (p, T). Into the atom and into its nucleus acted only
exactly balanced coulomb’s
and gravity forces
of differently (
(and back). This signified that eccentricity (e) of the orbit is
appeared as the quantum
parameter depended
on (p, T). Into the atom and into its nucleus acted only
exactly balanced coulomb’s
and gravity forces
of differently (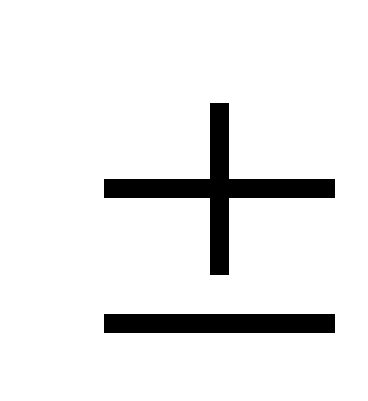 )
orientations. Therefore, so-called «nuclei
‘s forces»
are not existing. The circle
or the
straight-line
motions in Nature
are impossible in
order to a really curvature
in space and time. But as natural indicator
of this curvature may be namely the form
of body’s
trajectory.
)
orientations. Therefore, so-called «nuclei
‘s forces»
are not existing. The circle
or the
straight-line
motions in Nature
are impossible in
order to a really curvature
in space and time. But as natural indicator
of this curvature may be namely the form
of body’s
trajectory.
3.The real body’s trajectories in Nature
The explanation 2. It was shown in
the exp. 1 for the orbital body: W 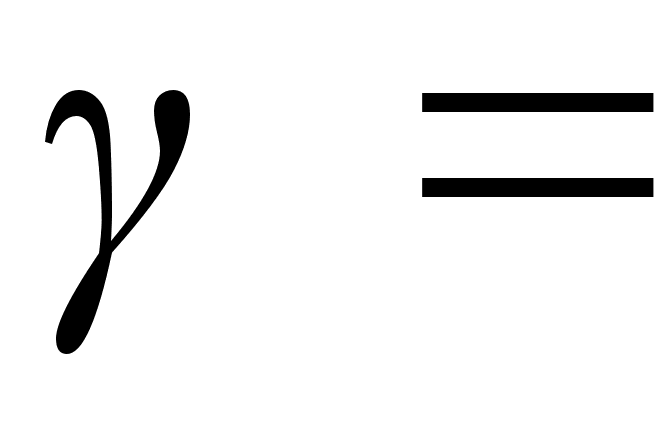
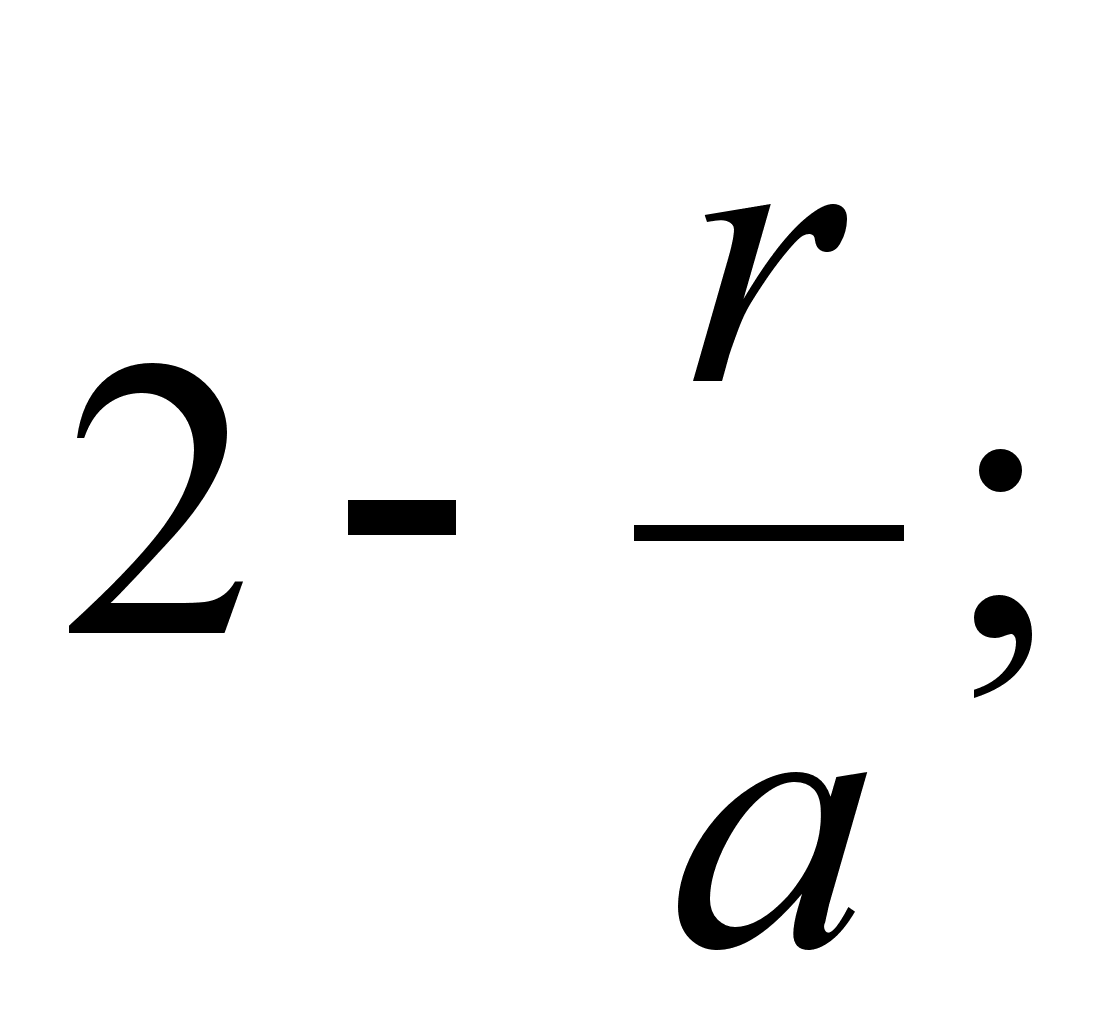 for
the non-orbital body: W>0,
for
the non-orbital body: W>0,
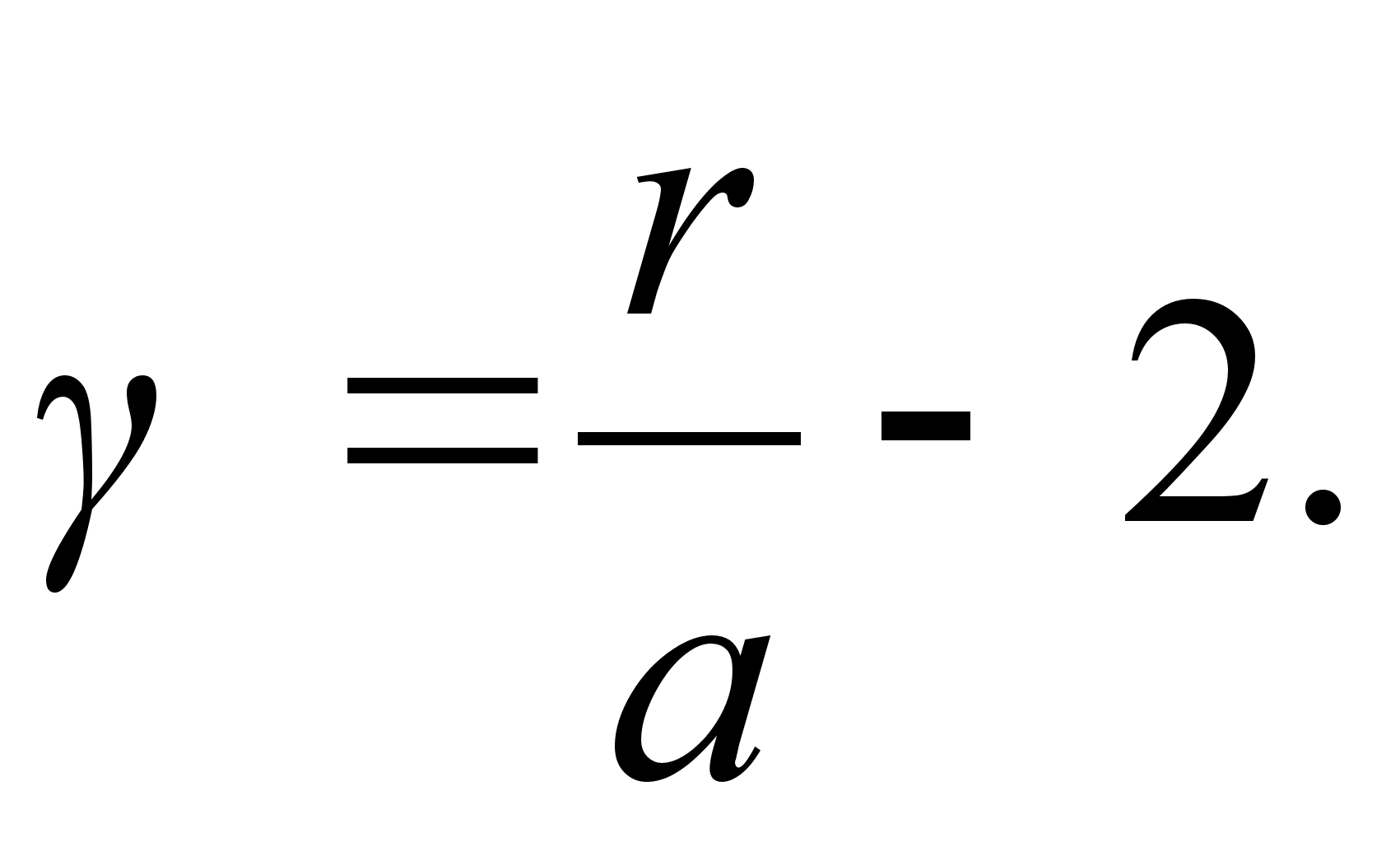
Write down the conical equation (for the circle, ellipse, parabola, hyperbola) in the non-dimensional forms
- for the ellipse
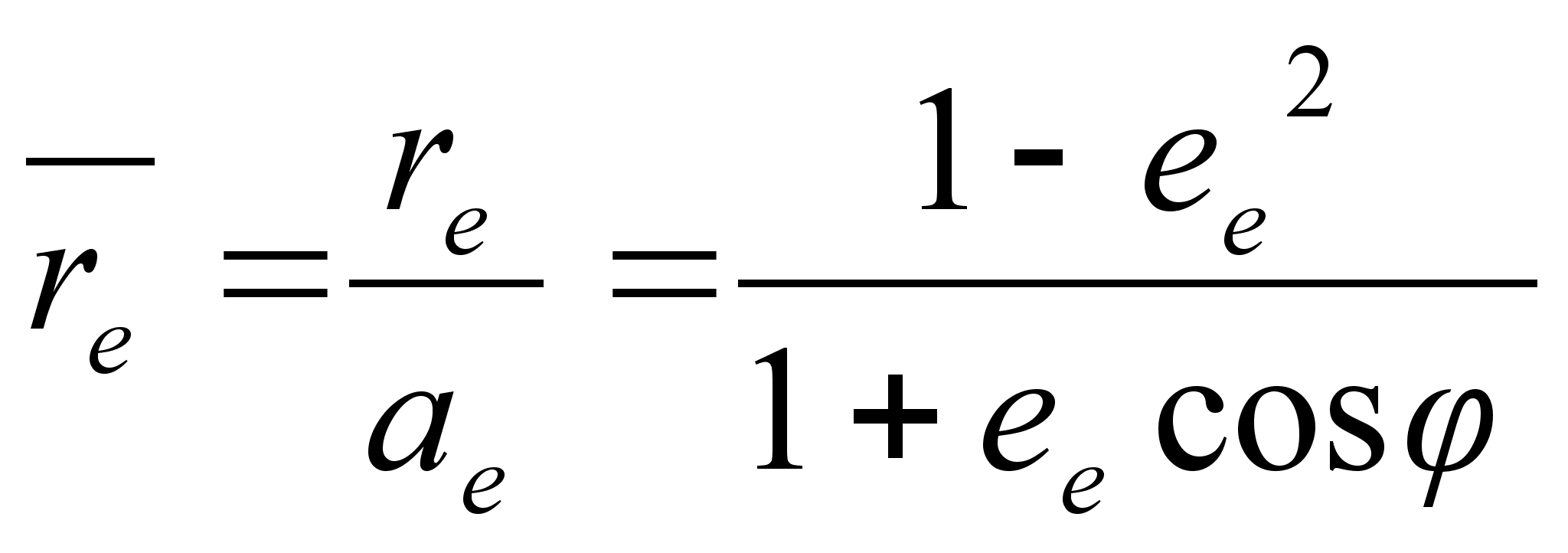 , where 0
, where 0 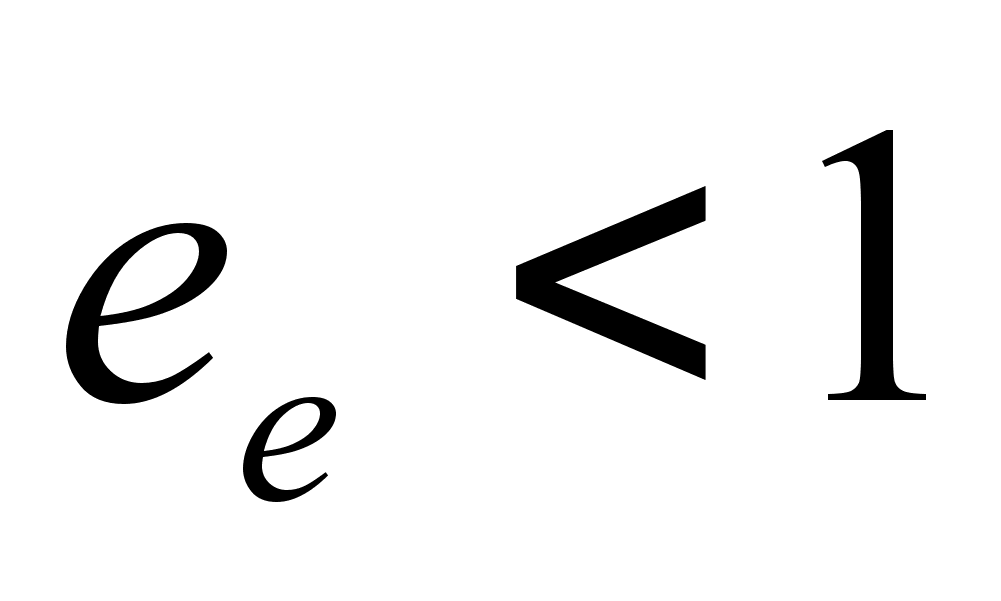 ,
(2)
,
(2)
- for the hyperbola
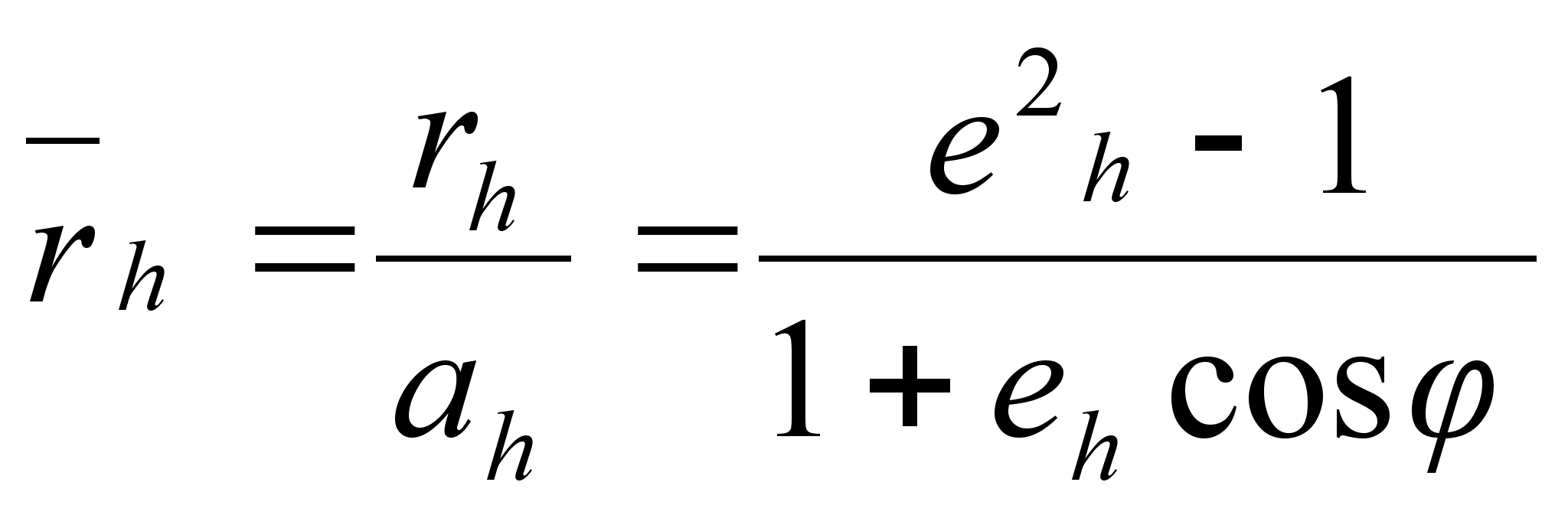 , where 1
, where 1 .
(3)
.
(3)
By means of (2), (3),(A) we obtain
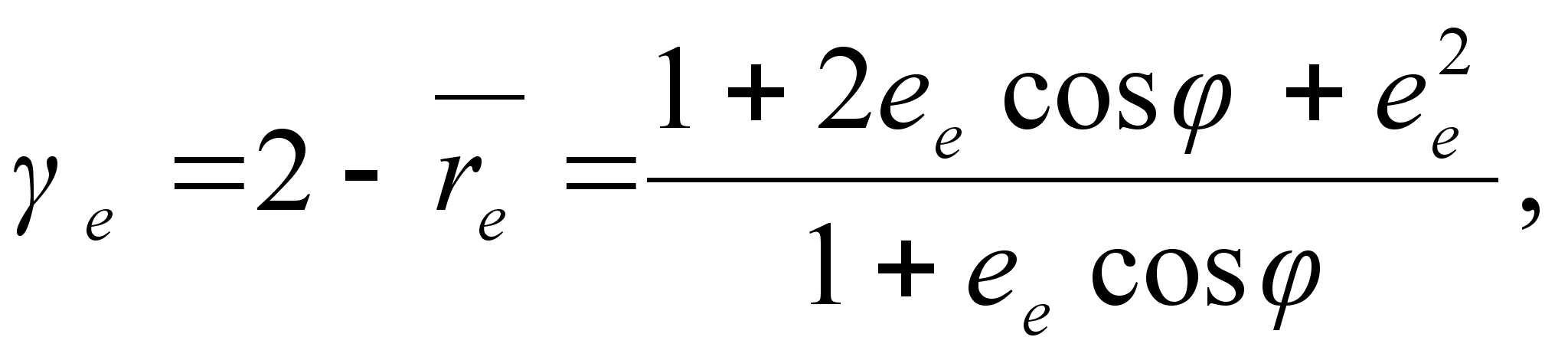
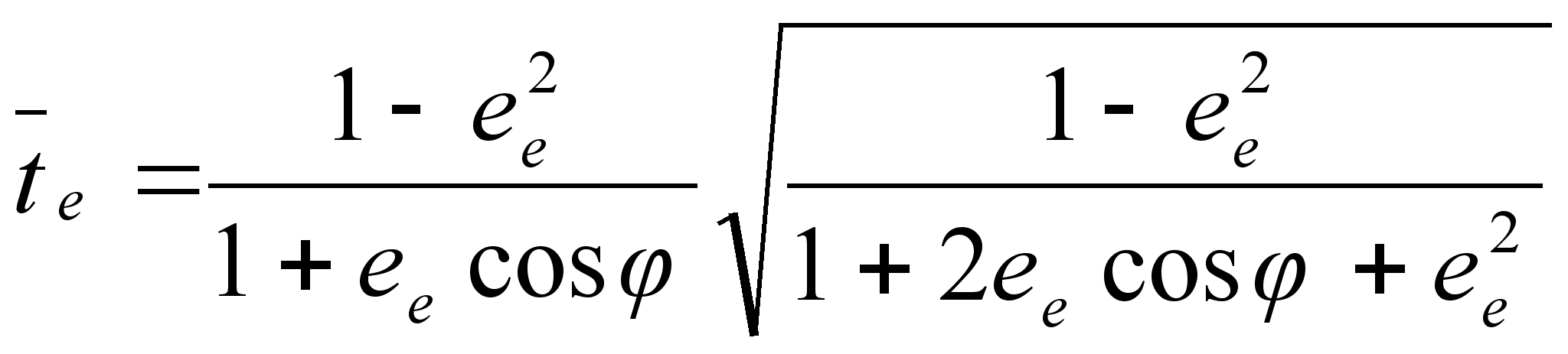 ,
where
,
where
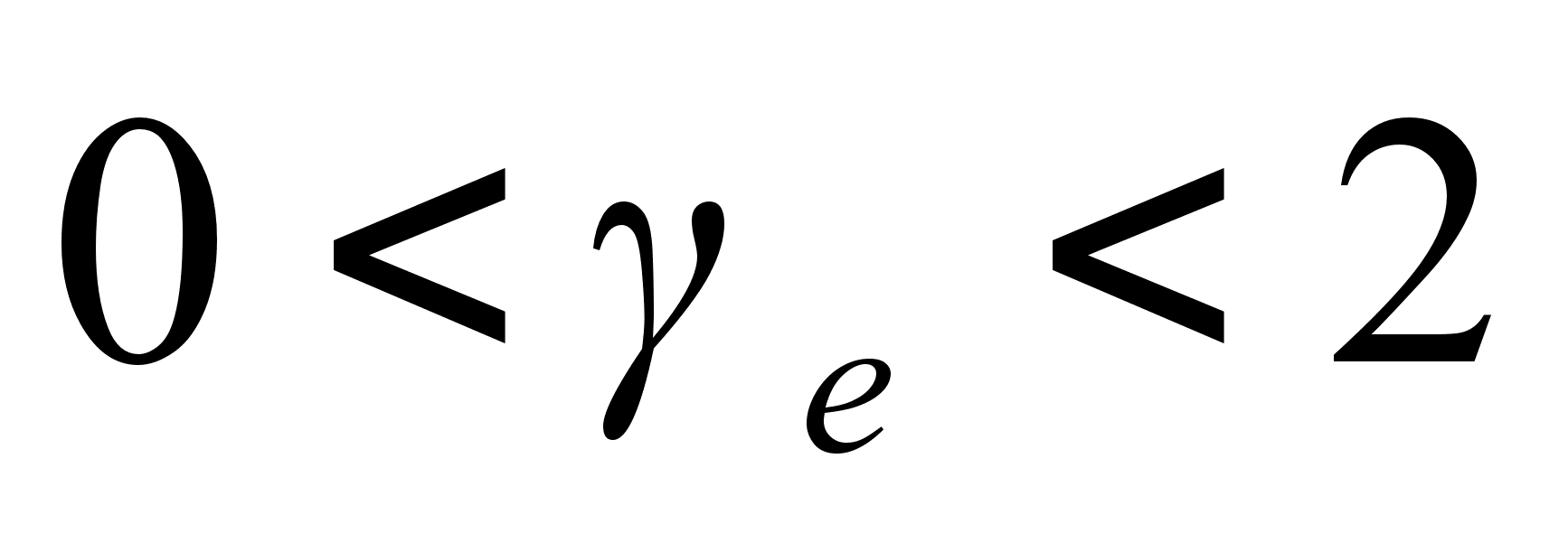 ,
(a)
,
(a)

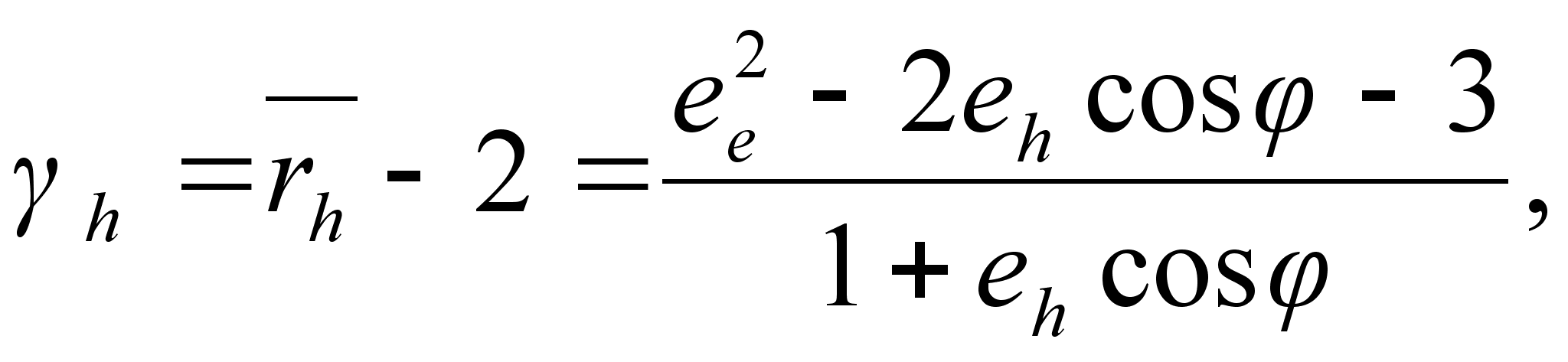
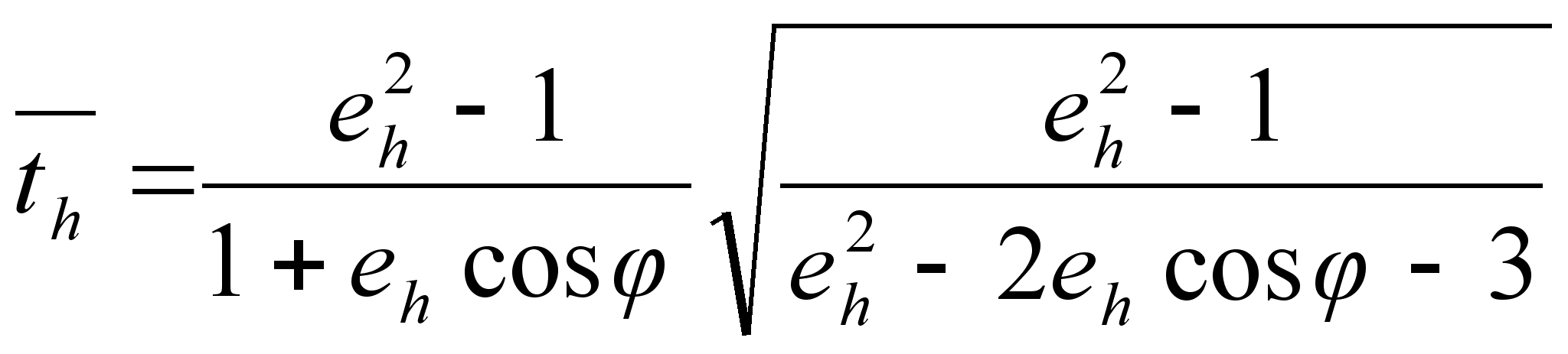 ,
where
,
where
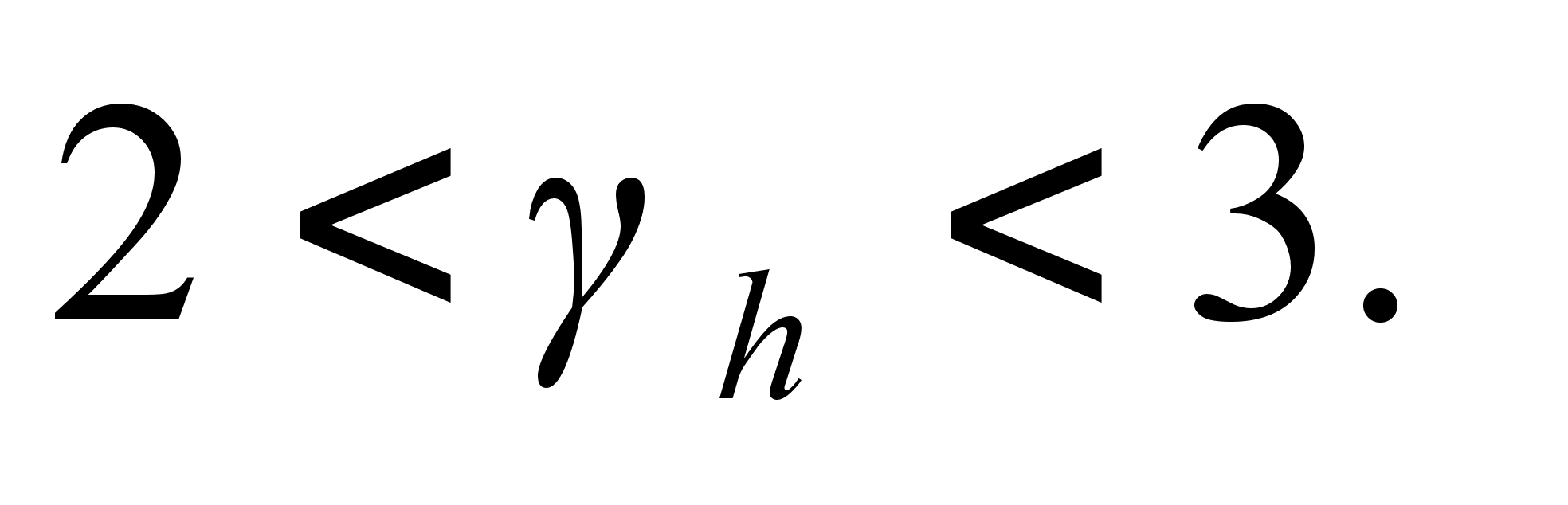 (b)
(b)
For the straight-line:
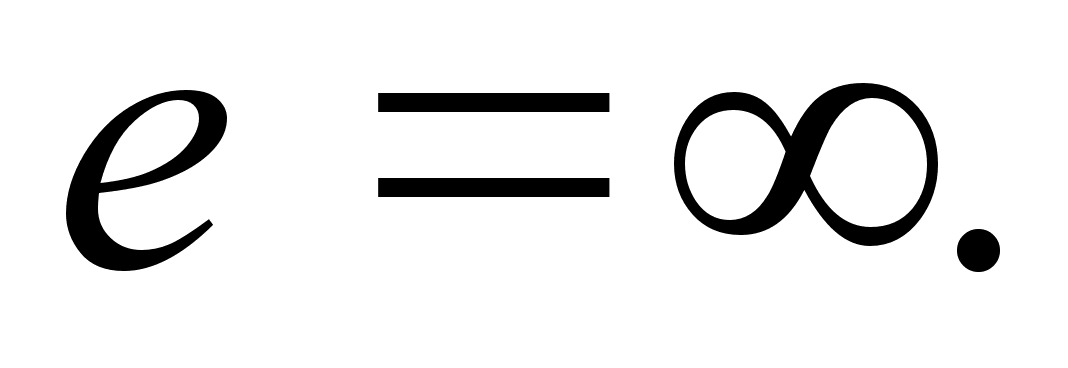 Therefore,
Therefore, (c). For the circle:
(c). For the circle:
 . Therefore,
. Therefore,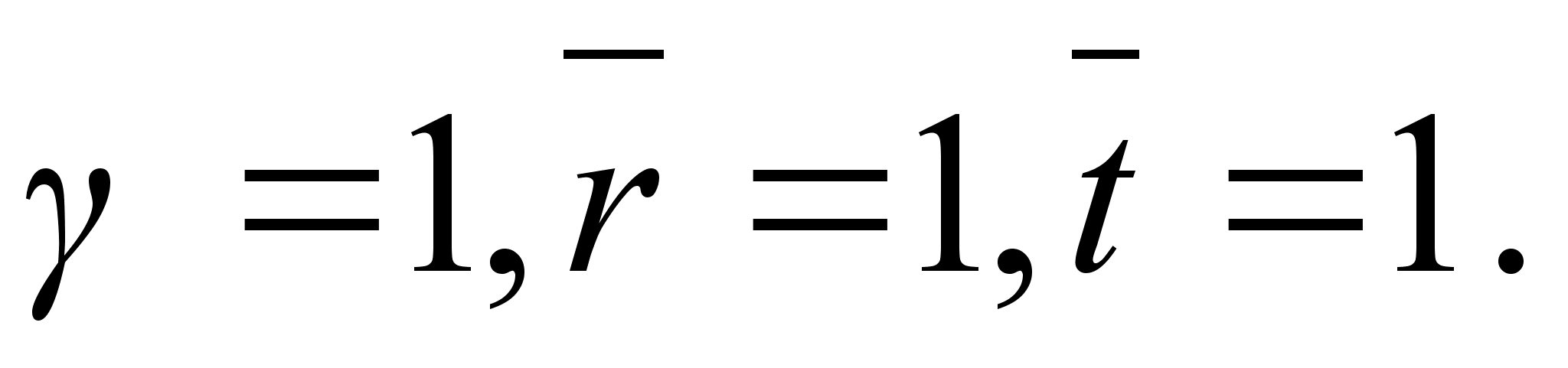 (d)
(d)
For the parabola: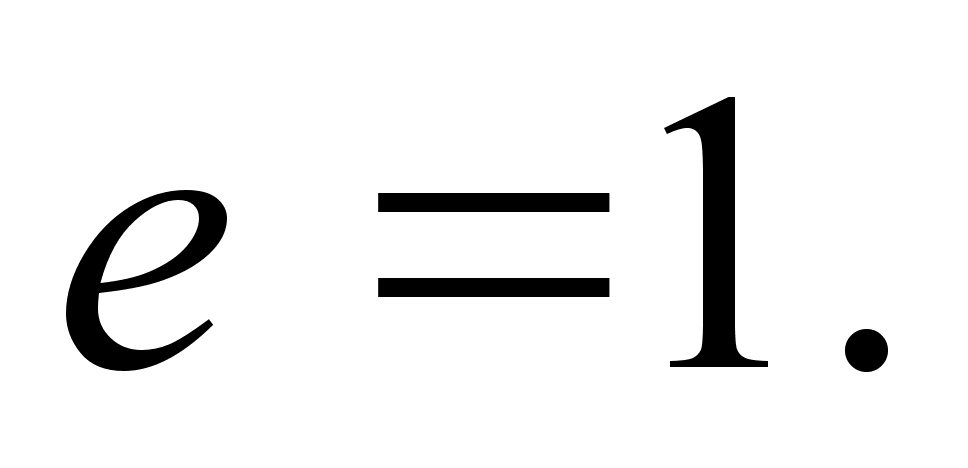 Therefore,
Therefore, (e).
But for the elliptical
and hyperbolical
trajectories parameters
(e).
But for the elliptical
and hyperbolical
trajectories parameters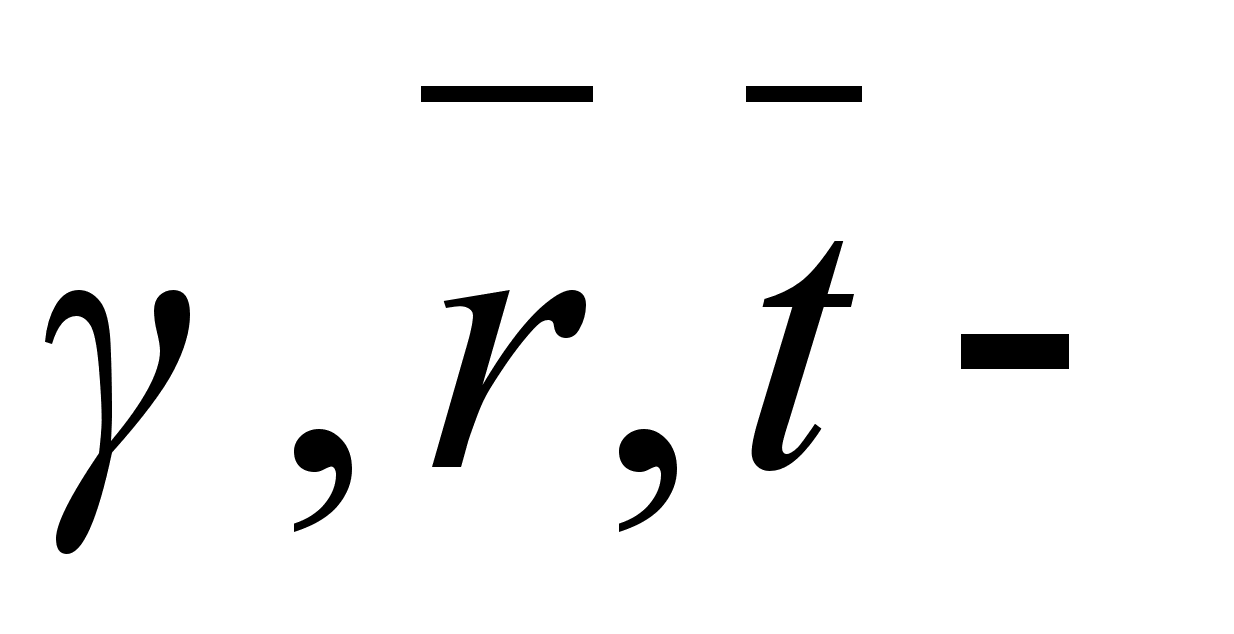 are
periodical ones.
are
periodical ones.
4.Some useful formulas
Cephler’s the Third law has the
next modern form (where f – the gravity constant, M –
mass of the Sun,
 - the orbit ‘s semi-axis,
- the orbit ‘s semi-axis,
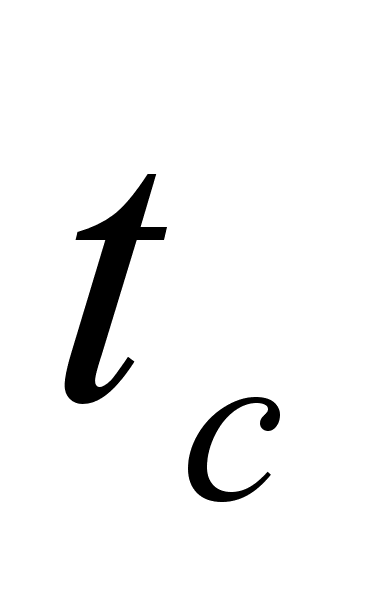 – period)
– period)
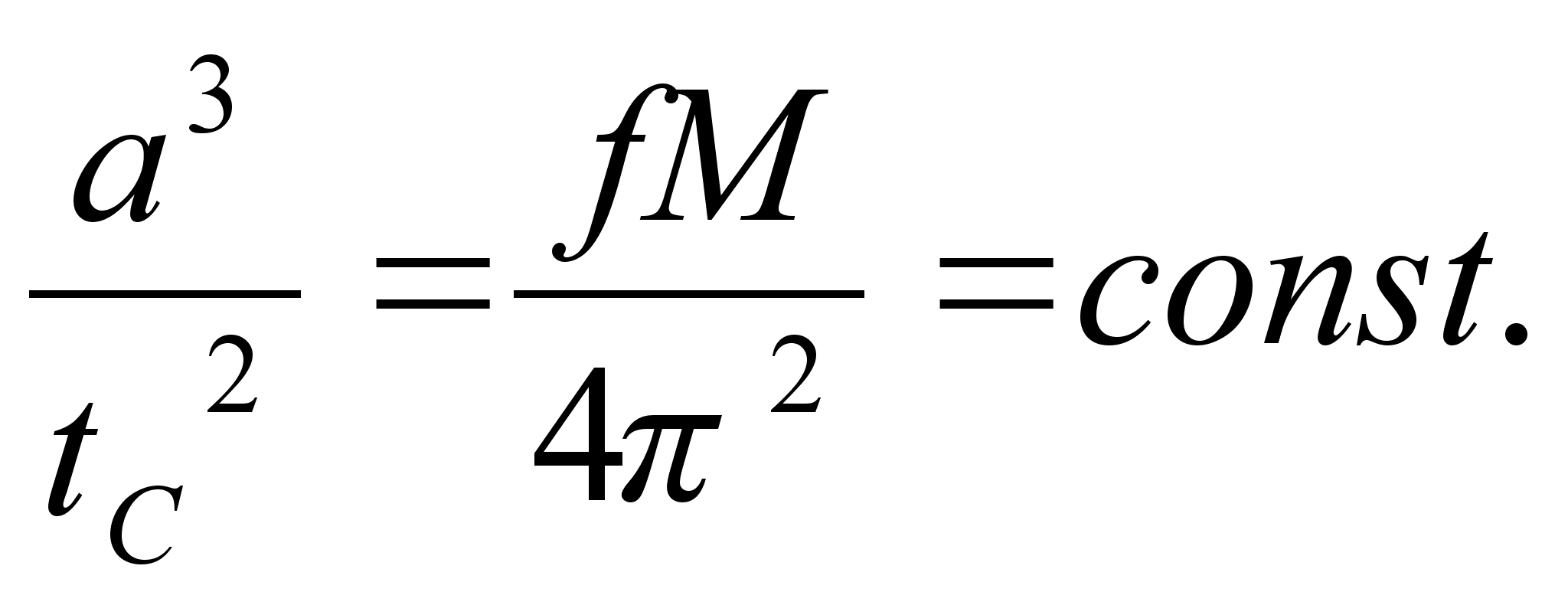 But as w=
But as w=
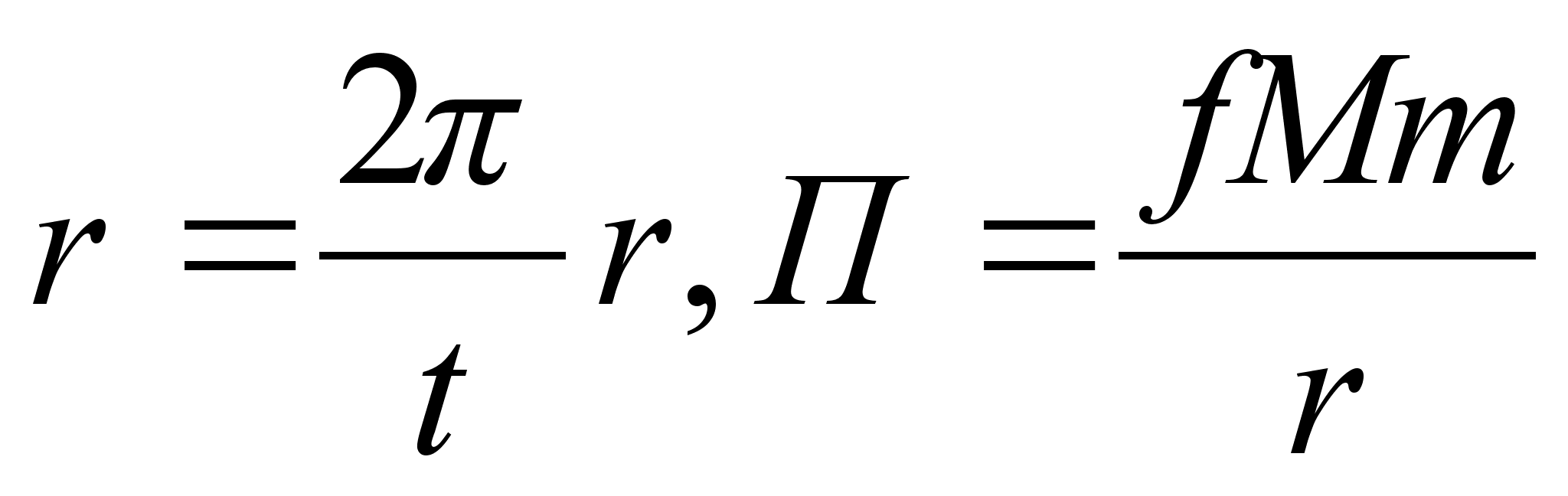 (where m – the planet’s mass) we obtain from (1)
(where m – the planet’s mass) we obtain from (1)

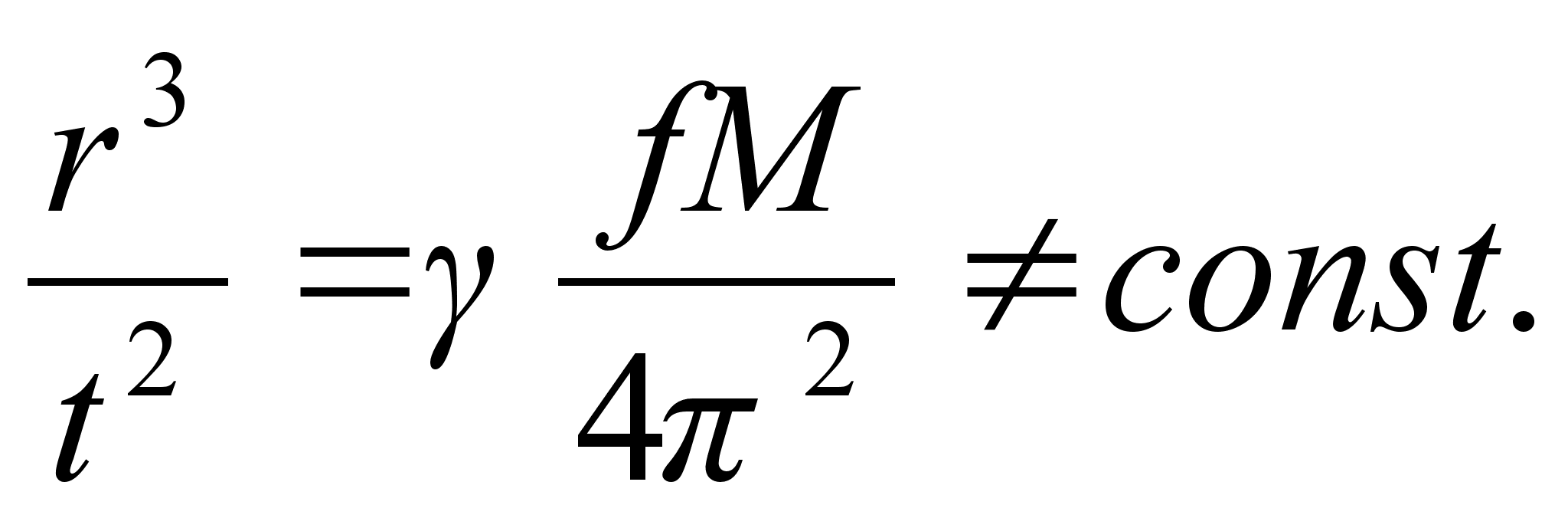 From these equations we obtain the correlation (A), where
From these equations we obtain the correlation (A), where
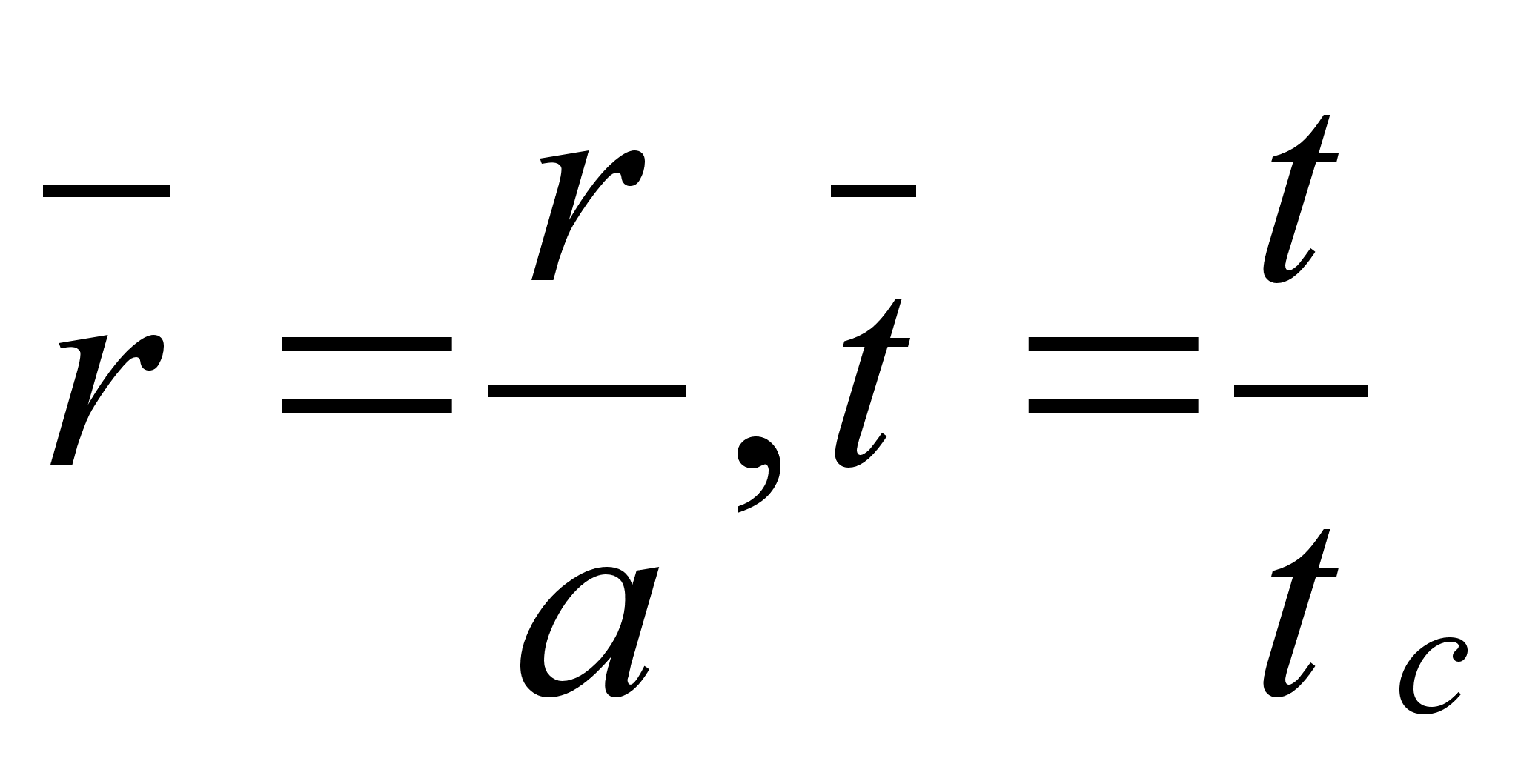 .
Also from the (1) we obtain: a)
.
Also from the (1) we obtain: a)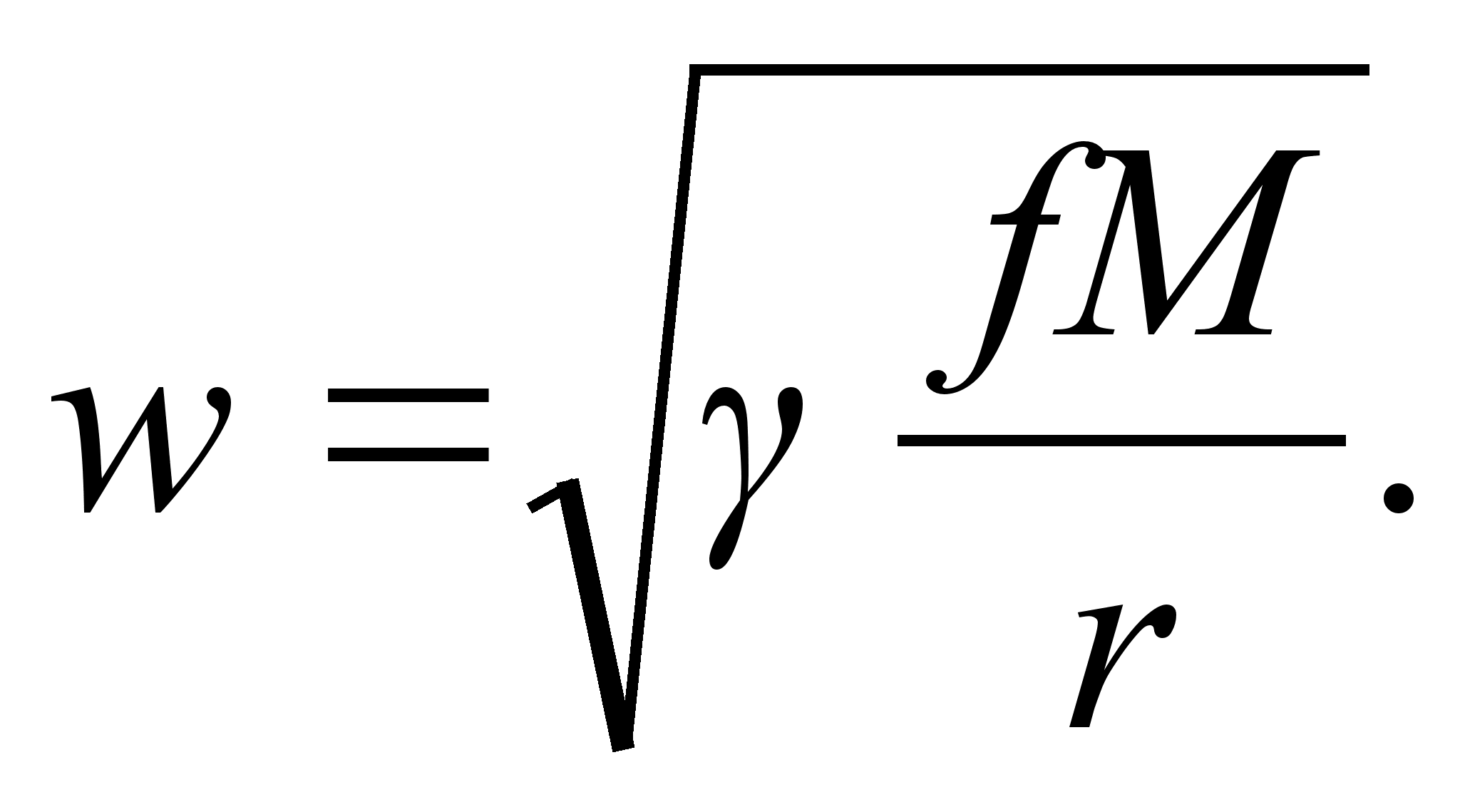 For the circle (
For the circle ( )
motion
)
motion
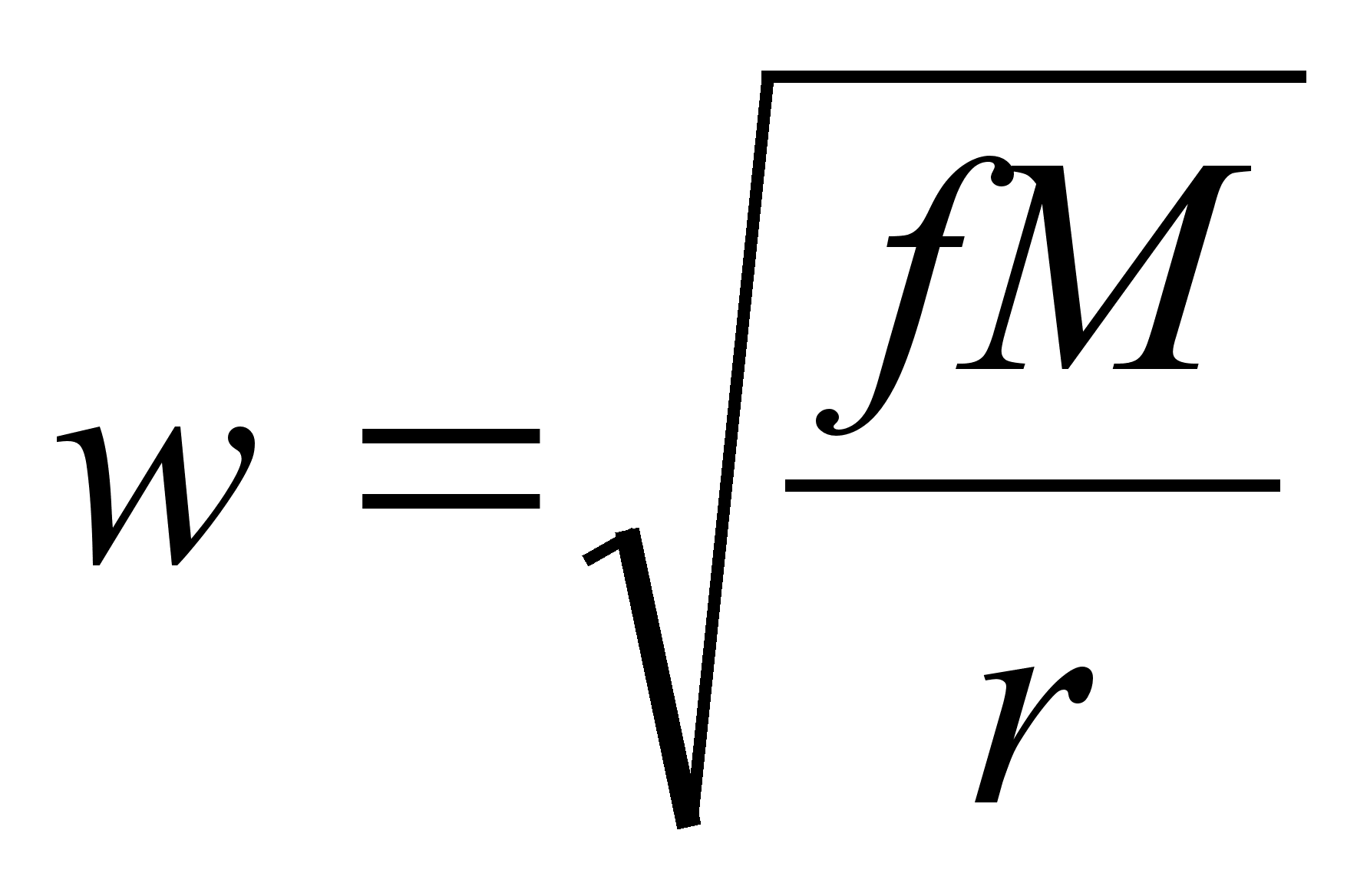 - the first
cosmic velocity. For the parabolic
(
- the first
cosmic velocity. For the parabolic
(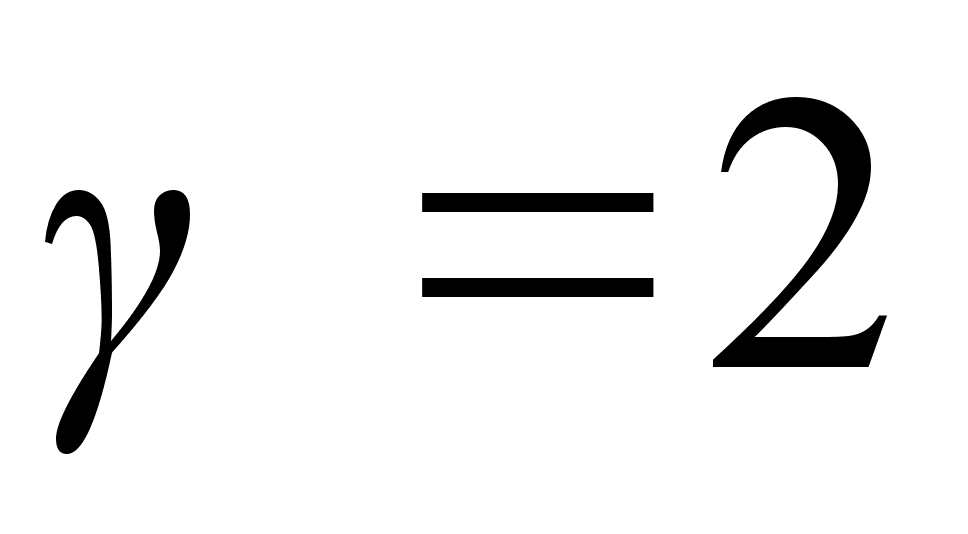 )
motion
)
motion
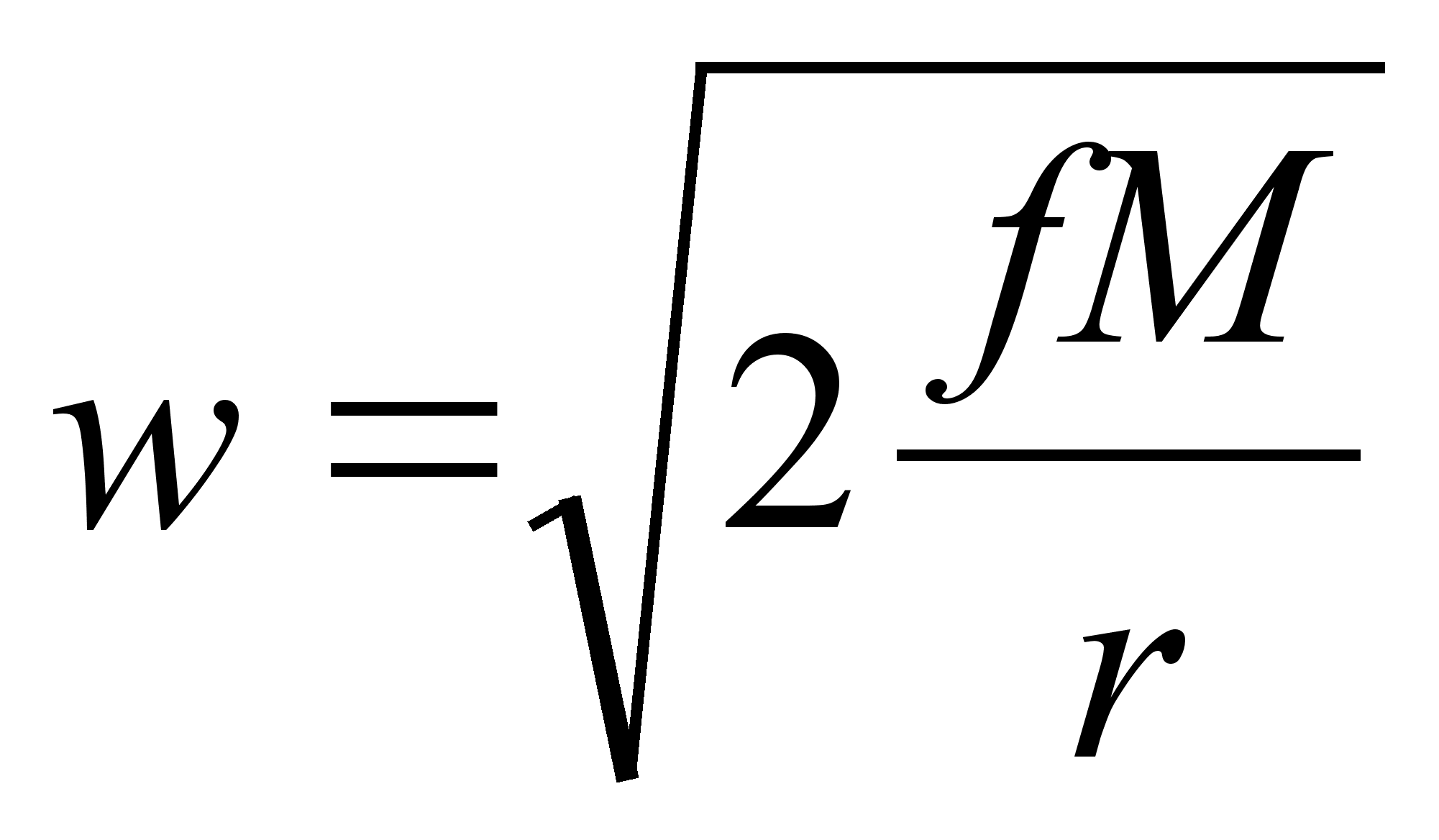 - the second
(or so-called - the «parabolic»)
cosmic velocity, and etc. b)
- the second
(or so-called - the «parabolic»)
cosmic velocity, and etc. b)
 (where M – the planet’s mass, r–the planet’s
radius,
(where M – the planet’s mass, r–the planet’s
radius,
 the
basis vector). Therefore, the body’s weight
(
the
basis vector). Therefore, the body’s weight
(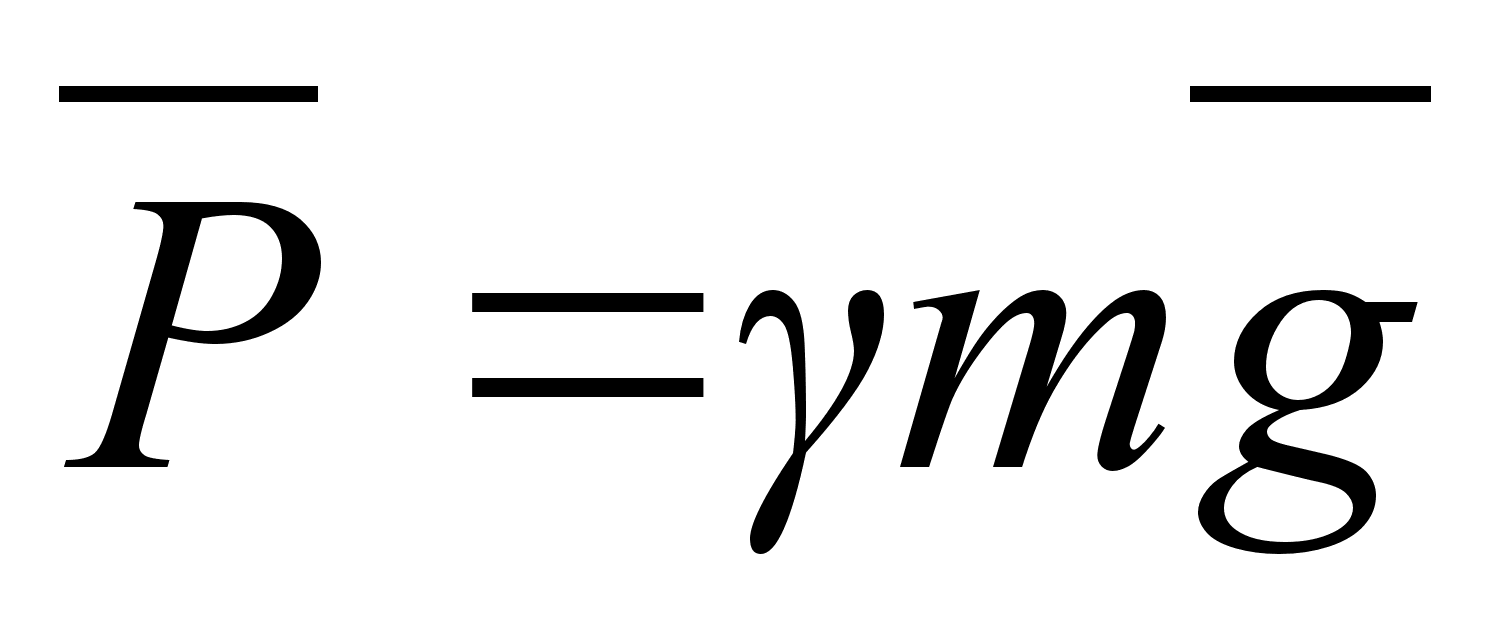 )
on the planet depended on the form
its orbit. For the circle
(
)
on the planet depended on the form
its orbit. For the circle
(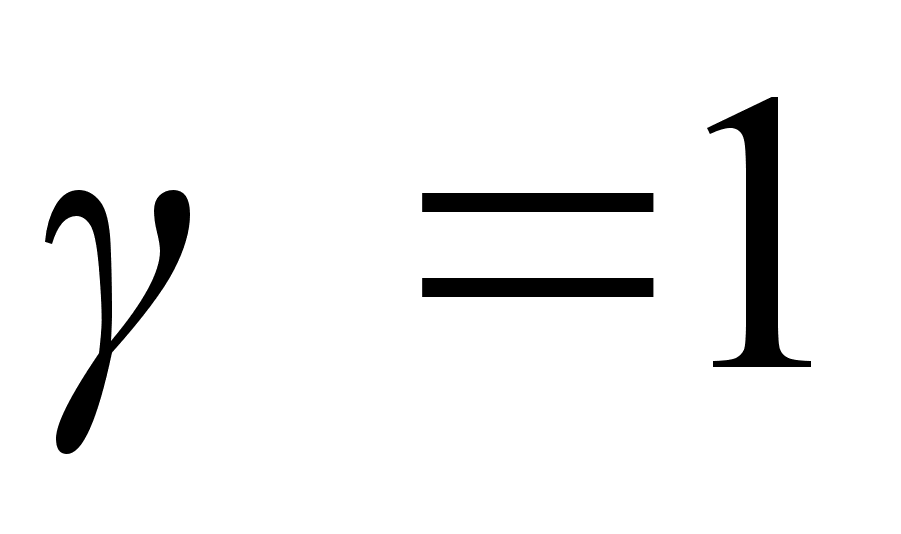 )
motion, we obtain:
)
motion, we obtain:
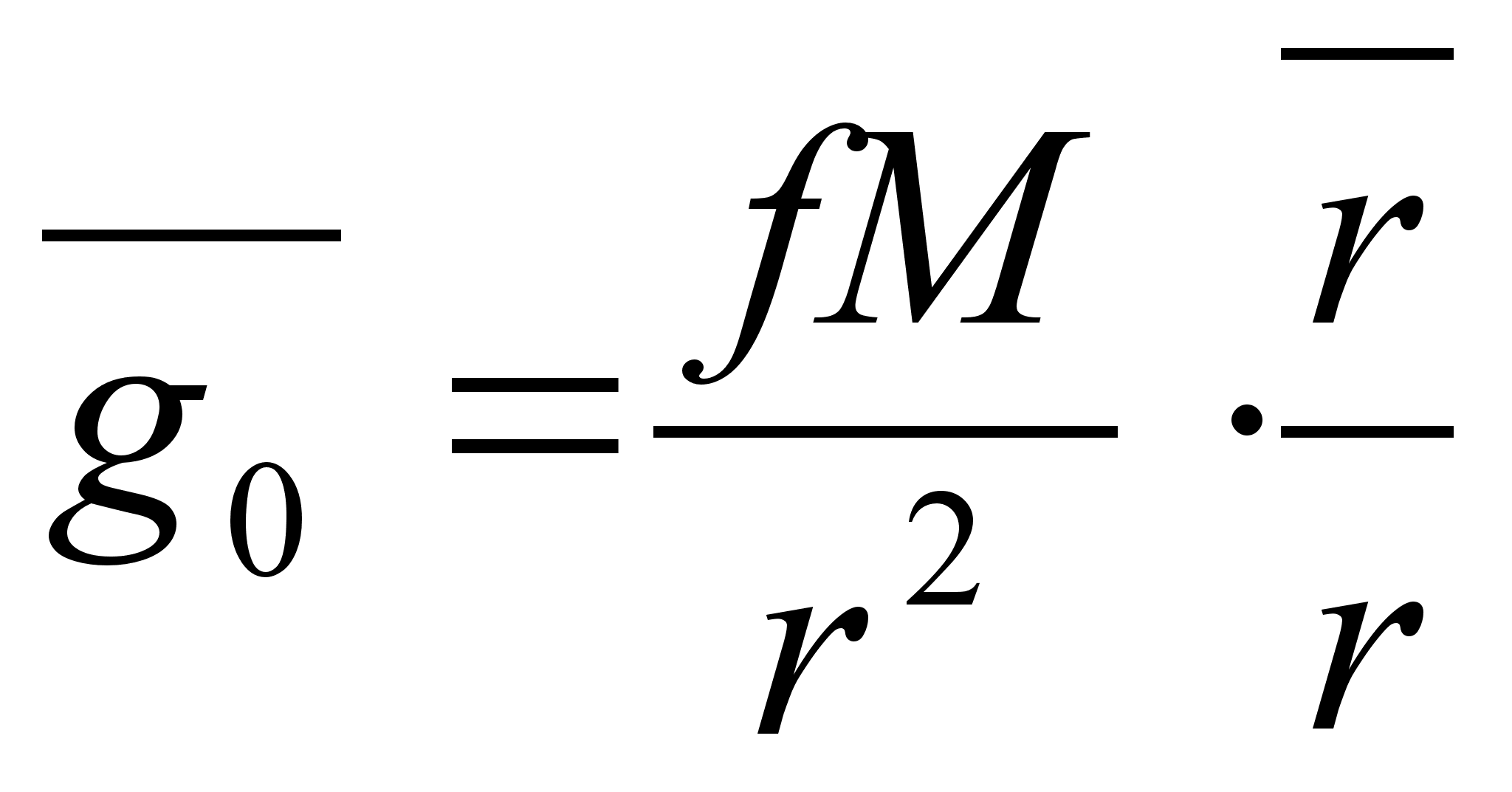 - the acceleration
of gravity. From
the (B’) for the photon
(
- the acceleration
of gravity. From
the (B’) for the photon
(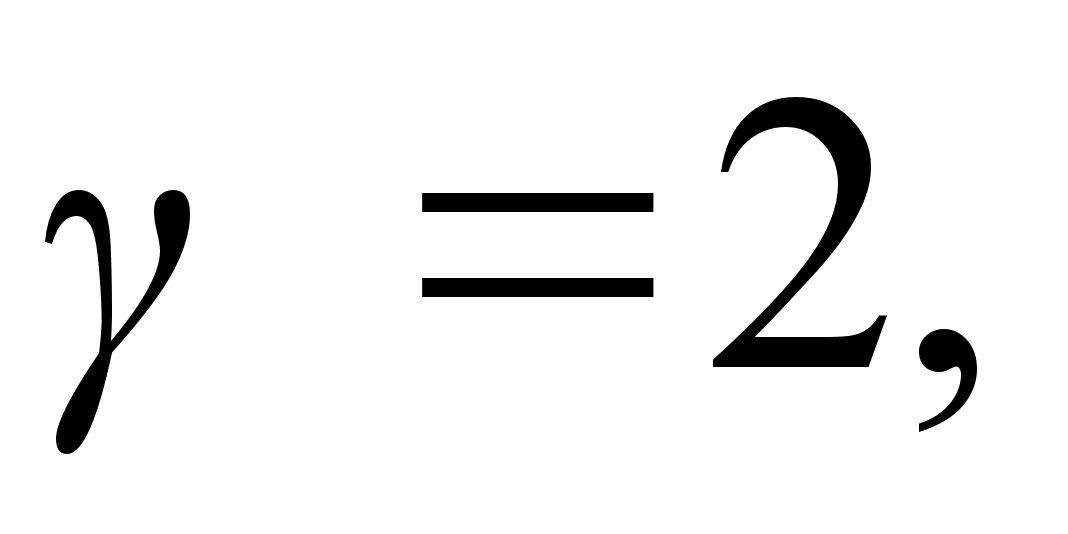
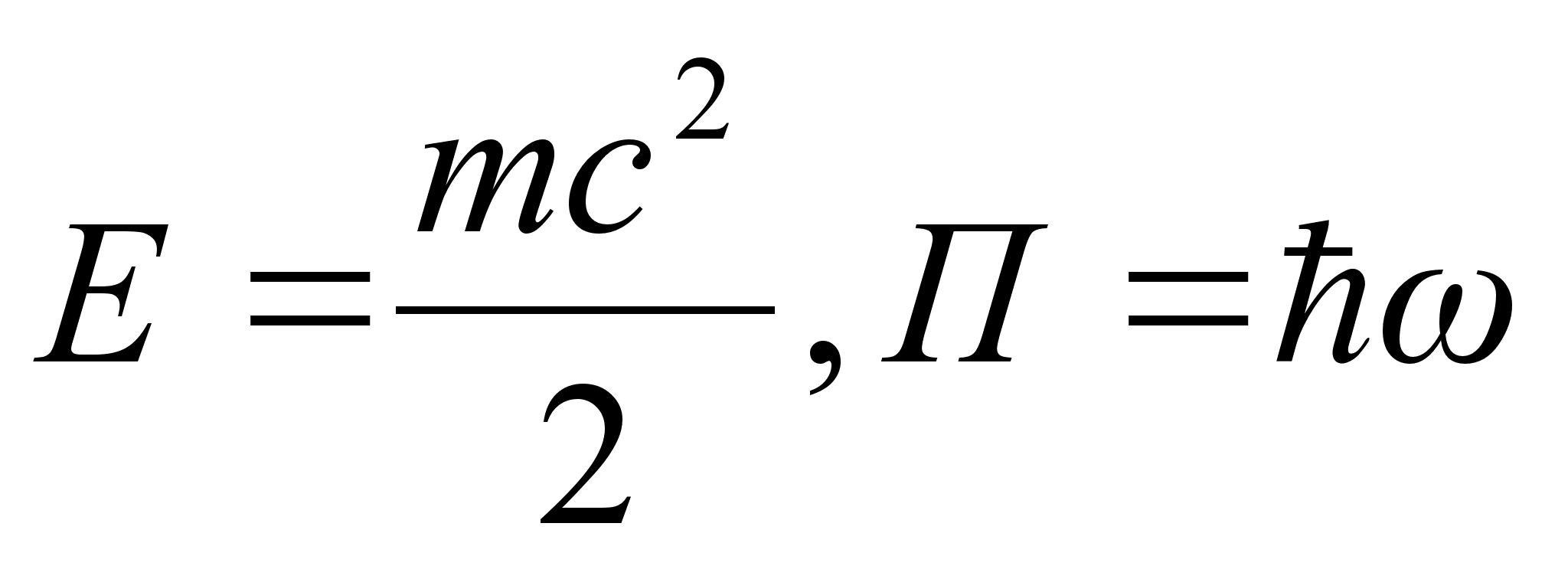 )
, we obtain :
)
, we obtain :
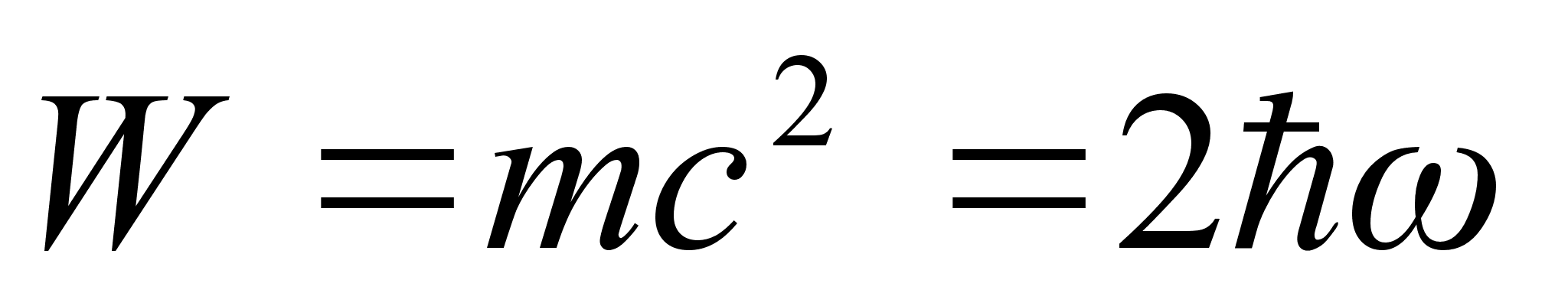 -
the full photon’s
energy. And etc.
You will be certained soon about the parameter
-
the full photon’s
energy. And etc.
You will be certained soon about the parameter
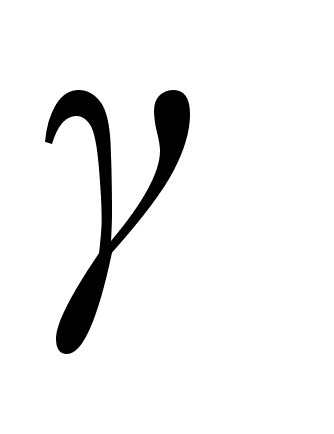
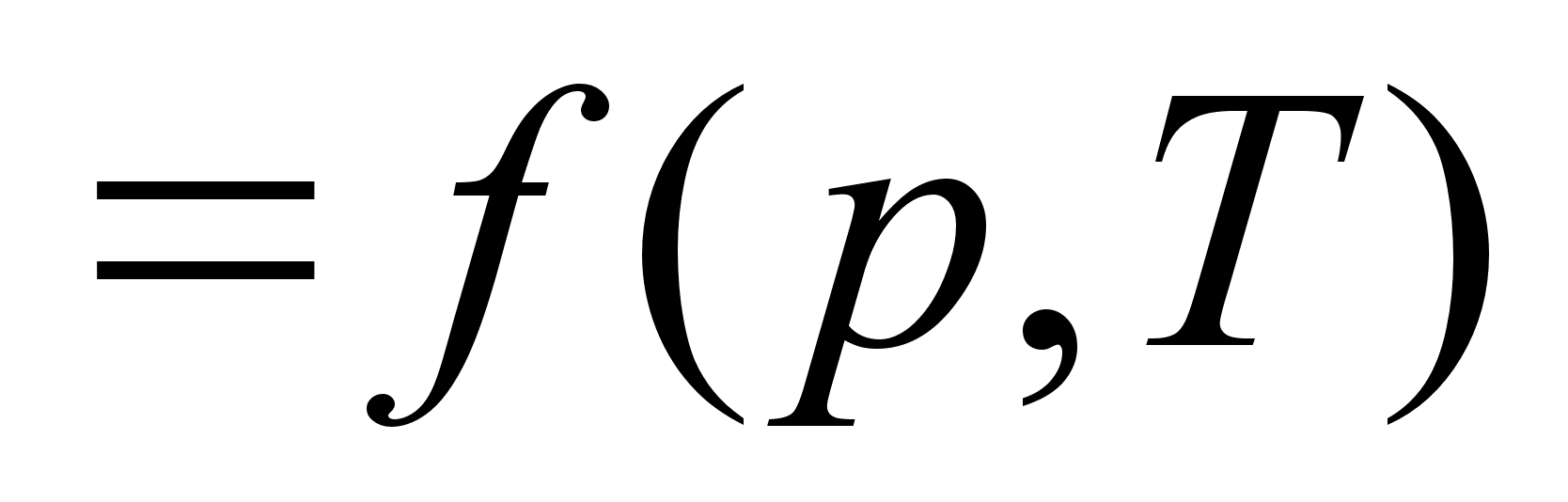 fundamental significance in
thermomechanics of macro- and microcosm.
fundamental significance in
thermomechanics of macro- and microcosm.
Thank you. To the next report in March, 08. G.I.G.