Реферат: Колебания системы Атмосфера - Океан - Земля и природные катаклизмы. Резонансы в Солнечной системе, нарушающие периодичность природных катаклизмов
ЯЛТИНСКАЯ МАЛАЯ АКАДЕМИЯ НАУК
ШКОЛЬНИКОВ «ИСКАТЕЛЬ»
Секция физики
Колебания системы « Атмосфера – Океан – Земля» и природные катаклизмы.
Резонансы в Солнечной системе, нарушающие периодичность природных катаклизмов.
Действительный член МАН Крыма «Искатель»
Ученик 11 класса
Форосской общеобразовательной школы I – III ступени г. Ялты
КОРАБЛЕВ Андрей
Научный руководитель – СЛАСТИХИН Л.П.
Учитель-методист физики
ВВЕДЕНИЕ.
В настоящее время в средствах массовой печати, в научно-популярной литературе, да и в солидных изданиях все катаклизмы на земле (чрезвычайные события) стали объясняться воздействием какого-то одного фактора. Многие провидцы и просто гоняющиеся за сенсациями журналисты из псевдонаучных изданий выдвигают “теории” о наступающем “конце света”. В мире все взаимосвязано и нельзя рассматривать одно в отрыве от другого. Я покажу на примере явления Эль-Ниньо то, как влияют межгодовые колебания системы Атмосфера-Океан-Земля на протекание различных физических явлений в атмосфере, в океане, на поверхности земли .
В последние месяцы в средствах массовой информации часто упоминаются чрезвычайные события (ураганы, наводнения, засухи, небывалые морозы и т.д.), вызванные возникшим в марте 1997 года явлением Эль-Ниньо – потеплением поверхностных вод в центральной и восточной частях Тихого океана. Давайте разберем причины участившихся чрезвычайных событий.
Явление Эль-ниньо неразрывно связано с явлением Южного колебания (перемещениями масс воздуха над тропическими частями Индийского и Тихого океанов в южном полушарии), поэтому оба явления изучают как единое явление Эль-Ниньо - Южное колебание (ЭНЮК), подразумевая под ним механические и термические колебания тропической атмосферы и океана периодом 2-10 лет. Будучи геофизическим явлением планетарного масштаба, ЭНЮК, как правило, приводит к тяжелым экологическим катастрофам, социально-экологические последствия которых ощушаются во всем мире.
Можно показать, что это явление – лишь одно из проявлений межгодовых (с периодами 2-10) совместных колебаний системы атмосфера-океан-Земля.Чтобы понять, как это происходит, рассмотрим колебания каждой из компонент в отдельности.
В системе Атмосфера – Океан - Земля имеют место автоколебания периодами 2-10лет. Первопричиной их являются, очевидно, флуктуации атмосферной циркуляции, которые обусловлены неравномерным разогревом атмосферы радиацией Солнца. Атмосферная циркуляция является основной причиной течений в океане. Взаимодействие атмосферной циркуляции с процессами в океане порождает колебания атмосферы и океана, которые раскачивают Землю. Поскольку Земля вращается вокруг своей оси, то ее колебания происходят не в плоскости какого-то меридиана, а по кругу – в виде нутаций. Географические полюсы Земли при этом совершают круговые движения. Движения полюсов вызывают полюсной прилив, который в свою очередь влияет на колебания атмосферы и океана. В итоге в системе атмосфера – океан Земля наблюдаются нелинейные колебания с характерными для них явлениями конкуренции, синхронизации и комбинационного резонанса. Вследствие нелинейности системы и изменений в климатической системе из-за деятельности человека или внешних факторов колебания носят нерегулярный характер.
Видимыми проявлениями совместных колебаний системы атмосфера - океан - Земля являются Южное колебание, Эль-Ниньо и Ла-Нинья и движения географических полюсов Земли. Явление ЭНЮК оказывает существенное влияние на гидрологический режим Мирового океана и аномалии погоды по всему земному шару, на жизнь биосферы. Продуктивность биосферы из – за воздействия ЭНЮК испытывает вынужденные колебания тех же периодов 2 – 10 лет. Во время Эль-Ниньо складывается крайне неблагоприятная экологическая обстановка для холоднолюбивых форм планктона, рыб, морских животных и птиц. Биологическая продуктивность Мирового океана заметно снижается. В период Ла-Нинья экологические условия становятся благоприятными и продуктивность восстанавливается. Мировой сбор зерновых и технических культур падает при Эль-Ниньо и растет при Ла-Нинья. Опасные явления погоды (сильные ливни, ураганы, морозы, засухи и т.п.) и связанные с ними стихийные бедствия (наводнения, оползни, пожары, аварии и т.п.) усугубляют негативные последствия эль-Ниньо.
Дальнейшие эмпирические и теоретические исследования, способствующие созданию моделей колебаний системы атмосфера – океан – Земля, позволят предвычислять их фазу, делать успешные прогнозы возникновения Эль-Ниньо и предупреждать тяжелые экологические и социально – экономические последствия.
Для исследования должны подвергаться анализу все сенсационные сообщения всех различных печатных изданий, однако анализ всех предсказаний нельзя проводить, используя изменения какого – то одного фактора, скажем, смещения магнитных полюсов. О влиянии на биосферу и цивилизацию надо анализировать по изменениям в Космосе, Океане, Земле.
КОЛЕБАНИЯ АТМОСФЕРЫ.
В 20-е гг. текущего столетия при анализе аномалий атмосферного давления в субтропической зоне Южного полушария было замечено, что, когда атмосферное давление повышено над Тихим океаном, над Индийским оно понижено, и наоборот. Это явление и было названо Южным колебанием. Позже выяснилось, что движение гигантских масс воздуха вдоль тропической зоны океанов, вызывающее чередование знака этих аномалий давления, напоминает гигантские качели.
|
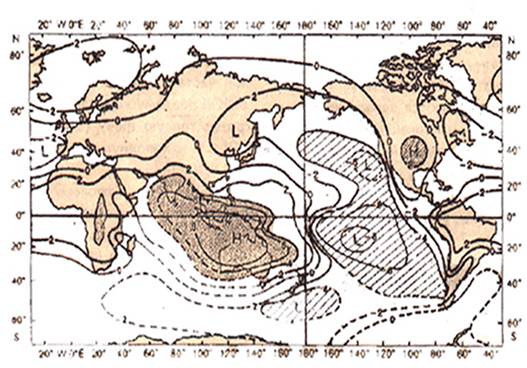
Рис. 1 Поле коэффициентов корреляции r между средними годовыми величинами атмосферного давления станции «Дарвин» (Австралия) и значениями давления в других пунктах Земли.
На рис. 1 показаны изолинии коэффициентов r ( увеличены в 10 раз). Для представленного случая в зоне от 300 с.ш. до 350 ю.ш. в Восточном полушарии коэффициенты корреляции положительные, а в Западном полушарии отрицательные.
Коэффициент корреляции r в рассматриваемом случае является мерой линейной статистической связи между многолетними величинами атмосферного давления в одном пункте (в нашем случае станция «Дарвин» (Австралия)) и другими пунктами земного шара. Чем ближе его величина к 1 или –1, тем теснее связь между величинами атмосферного давления в исследуемых пунктах.
Имеются своего рода два центра действия противоположного знака: австралийско – индонезийский и южнотихоокеанский. Оба расположены в тропиках Южного полушария ( отсюда и название Южное колебание).
Очаг наиболее тесной отрицательной корреляции (r < - 0,8 ) располагается вблизи станции «Таити» (170 ю.ш. , 1500 з.д.), поэтому в качестве индекса нужного колебания SOI ( South Oscillation Index) используют разность нормализованных аномалий давления на метеостанцях «Таити» и «Дарвин». При SOI £ 0 давление понижено над Тихим океаном и повышенно над Индийским океаном, при SOI ³ 0 картина обратная.
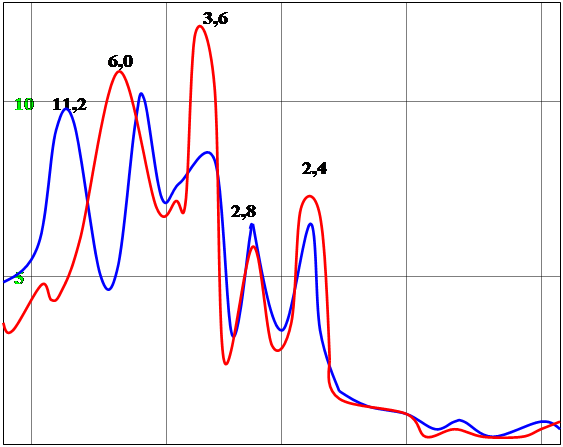
При первом взгляде на многолетние кривые индекса SOI, который фиксировался непрерывно с 1866 года, создается впечатление, что чередование его фаз носит случайный характер. Однако спектральный анализ показал наличие ярко выраженных преимущественных периодов: 6; 3,6; 2,8; 2,4 года ( рис. 2, красная кривая 1). Имеется также небольшой пик около 12 лет. Важно, что все эти преобладающие периоды ( за исключением периода 2,8 г.) примерно кратны периоду 1,2 г. ( номера гармоник nk = 5; 3; 2 и 10 соответственно).
70 20 10 7 5
Рис. 2 Спектры мощности двух самых длительных рядов индексов SOI с 1866 г. по 1996 г. ( красная кривая) и сходных с ним индексов DT с 1851 г. по 1996 г. ( синяя кривая). По оси абсцисс приведены периоды в кварталах, по оси ординат – спектральная плотность.
КОЛЕБАНИЯ ОКЕАНА.
Явление Южного колебания тесно связано с процессами в океане. При положительных SOI ( ³ 0 ) северо – восточные и юго – восточные пассатные ветры, дующие в тропиках Тихого океана, нагоняют теплую воду в его западную часть. Там образуется толстый слой теплого перемешивания. Глубина термоклина – тонкого слоя воды, отделяющего верхний перемешанный слой от глубинных слоев океана, в котором температура очень быстро падает с глубиной, - составляет 200 – 300 м., а температура воды на поверхности достигает 27 – 300 С. Наоборот, в тропиках восточной части Тихого океана в результате сгона формируется холодный и тонкий слой перемешивания. Глубина термоклина не превышает 50 м., а температура воды колеблется от 20 – 250С в океане до 15 – 190С у побережья Южной Америки.
Когда индекс SOI уменьшается и становится отрицательным, направленный к западу градиент давления тоже уменьшается, вплоть до обращения знака, пассатные ветры ослабевают и иногда меняют направление на противоположное: появляются западные ветры. Теплая вода, накопившаяся в западной части Тихого океана, не испытывая сопротивления ветра, устремляется на восток в форме внутренней экваториальной волны, распространяющейся со скоростью 2 – 4 м/с. Когда эта волна достигает берегов Южной Америки, вода накапливается, повышается уровень моря, углубляется граница термоклина, волна движется далее, отворачивая к полюсам, и в виде отраженной волны на запад. В результате этого область теплой воды быстро расширяется. Такие случаи потепления вод в центральной и восточной частях экваториальной зоны Тихого океана и получили название явления Эль-Ниньо.
В отличие от термина Эль-Ниньо, которым пользуются рыбаки Перу для описания локального сезонного теплого течения у берегов Перу и Эквадора, явление Эль-Ниньо охватывает всю центральную и восточную части экваториальной зоны Тихого океана и экваториальную зону Индийского океана, что придает ему глобальное значение.
Эль-Ниньо неразрывно связано с Южным колебанием. Установлено, что чем больше SOI, тем ниже температура поверхности восточной и центральной частей Тихого океана. В явлении ЭНЮК поэтому выделяют две крайние фазы: теплую фазу (Эль-Ниньо) при SOI £ 0 и холодную фазу (Ла-Нинья) при SOI ³ 0.
При Эль-Ниньо уровень моря в восточной части Тихого океана примерно на 50 см. выше, чем в западной части, при Ла-Нинья – картина обратная. Это значит, что в тропической зоне имеются межгодовые колебания уровня моря между восточной и западной частями Тихого океана амплитудой примерно 50 см. Спектр этих колебаний аналогичен спектру SOI.
Со времени пионерских работ Дж. Бьеркнеса считается, что ЭНЮК есть самоподдерживающееся колебание, в котором аномалии температуры поверхности экваториальной части Тихого океана влияют на интенсивность пассатных ветров. Последние управляются океаническими течениями, а те в свою очередь формируют аномалии температуры поверхности океана.
Обычно строятся нелинейные модели взаимодействия океана с пассатными ветрами и исследуется поведение моделей в зависимости от амплитуды сезонного цикла температуры воды и скорости течения, параметров, характеризующих силу трения атмосферы с океаном, вариаций термоклина и т.п. В частности, показано, что при изменении во времени параметров сцепления и сезонного воздействия на экваторе возникают совместные колебания аномалий температуры океана, скорости течения и глубины термоклина с периодом 3 – 4 года и их гармоники. Когда температура воды и скорости течения изменяются в течение года, предельный цикл становится странным аттрактором – зоной фазового пространства, к которой притягиваются фазовые траектории и в которой изображающая точка совершает хаотическое движение, лишенное свойства повторяемости. Наличие хаоса расширяет и размазывает главные энергетические пики в спектре и сдвигает их в сторону низких частот. Годовые вариации основного состояния не только порождают нерегулярности периода колебаний, но и приводят к синхронизации колебаний с годовым циклом, в результате чего появляются субгармоники с периодом 3,4 и 5 лет.
Таким образом, все современные модели трактуют ЭНЮК как автоколебания совместной системы океан – атмосфера, не обращая внимания на то, что в спектре присутствуют составляющие, кратные не 1 году, а 1,2 года. Период 1,2 года, названный по имени его первооткрывателя периодом Чандлера, - это период свободного движения географических полюсов Земли. Он определяется сжатием и упругими свойствами Земли, поэтому естественно было предположить, что колебания ЭНЮК есть колебания не двойной системы океан – атмосфера, а тройной: атмосфера – океан – Земля.
ДИНАМИКА ВРАЩАЮЩИХСЯ ТЕЛ.
Прежде чем перейти к рассмотрению значения колебаний Земли в механизме явления ЭНЮК рассмотрим свойства нашей планеты как вращающегося тела. Нам необходимо ввести понятия прецессии и нутации.
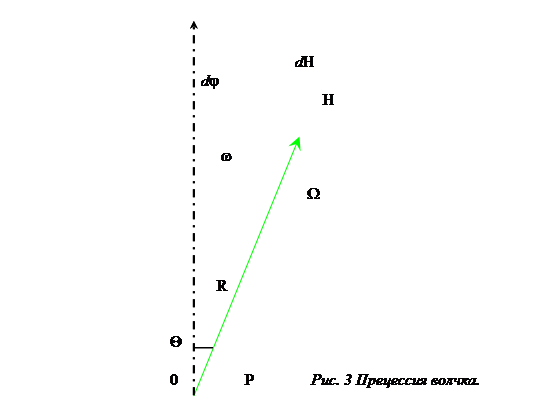
Рассмотрим быстро вращающийся волчок. Пусть его ось вращения отклонена от вертикали на угол Q ( см. рис 3)
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()


На волчок действует сила тяжести P = mg, где m – масса волчка, g – ускорение силы тяжести. Невращающееся тело под действием силы тяжести падает. В случае волчка падения не наблюдается. Ось его вращения непрерывно смещается, но не в направлении силы тяжести, а в перпендикулярном ей направлении, описывая конус вокруг вертикали. Это движение оси волчка называется прецессией. Чтобы понять, почему так ведет себя волчок, проанализируем его динамику.
Вектор момента импульса волчка равен H = JW, где J – момент инерции волчка относительно его оси вращения, W - вектор угловой скорости. Сила тяжести Р создает момент силы L относительно точки опора О: L = [ R x P ], где R – радиус – вектор центра тяжести. Под действием момента силы L момент импульса волчка
dH
![]() изменяется со скоростью = L.
Поскольку вектор L направ-
изменяется со скоростью = L.
Поскольку вектор L направ-
dt
лен перпендикулярно векторам R и Р, и вектор Н совпадает по направлению с R , то конец вектора Н и с ним ось вращения волчка смещаются в направлении, перпендикулярном направлению силы тяжести Р. При отсутствии трения вектор Н меняется только по направлению, т.е вращается, описывая конус с вершиной в точке опоры О.
Какова угловая скорость w прецессии волчка? За промежуток времени dt вектор Н получает перпендикулярное себе приращение dН = L dt, лежащее в горизонтальной плоскости. Отношение dН к проекции вектора Н на горизонтальную плоскость НsinQ дает угол dj поворота этой проекции за время dt:
L
![]() dj = dt
dj = dt
НsinQ
Производная dj / dt является искомой угловой скоростью прецессии:
L mgRsinQ mgR
![]()
![]()
![]() w = = =
w = = =
HsinQ JW sinQ JW
Итак, угловая скорость прецессии прямо пропорциональна величине момента силы тяжести и обратно пропорциональна моменту импульса волчка. Направление прецессии определяется правилом: момент силы L заставляет отрезок RsinQ вращаться около точки О в направлении к вектору L.
Более строгое рассмотрение показывает, что, помимо прецессии, ось волчка совершает быстрые колебания малой амплитуды. Эти колебания ( дрожание оси ) называются нутацией ( от лат. Nutatio – колебание ). Удвоенная амплитуда Q - Q0 и период t нутации волчка приближенно равны:
2АmgRsinQ0 2pA
![]()
![]() Q - Q0 » ;
t »
Q - Q0 » ;
t »
(JW)2 JW
где Q и Q0 - пределы изменения угла Q в результате нутации, А – момент инерции волчка относительно оси, проходящей через точку О перпендикулярно оси вращения.
Как известно, Земля вращается вокруг своей оси со скоростью 7,29 . 10-5 рад /с. Угол наклона этой оси к плоскости земной орбиты – эклиптике – равен 660 33’ . Момент инерции Земли огромен – 8,04 . 1037 кгм2 . Фигура Земли близка к фигуре эллипсоида вращения. Когда Луна и Солнце не лежат в плоскости земного экватора, их силы притяжения стремятся развернуть Землю так, чтобы экваториальные вздутия располагались по линии, соединяющей центр масс Земли с Луной и Солнцем. Но так же, как волчок, Земля не поворачивается в этом направлении, а под действием момента пары сил, действующих на экваториальные вздутия, прецессирует. Земная ось медленно описывает конус вокруг перпендикуляра к плоскости эклиптики (рис. 4).
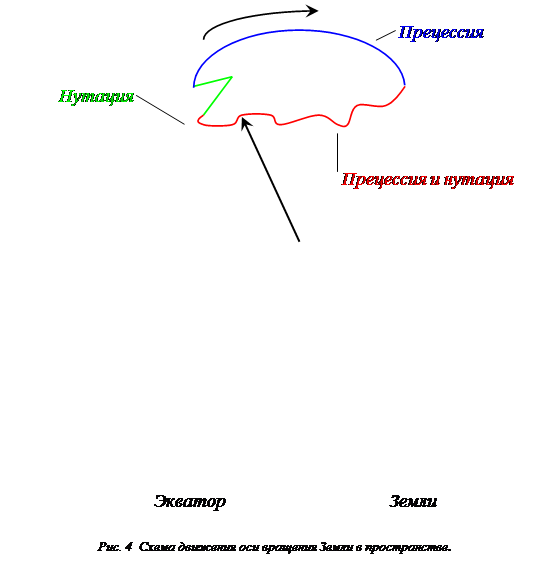
Вершина конуса совпадает с центром Земли. Так как момент импульса Земли очень велик (59 . 1032 кг . м2 . с-1 ), скорость прецессии очень мала ( период равен примерно 26 тыс. лет). Угол наклона земной оси к эклиптике при прецессии не меняется, оставаясь равным 660 33’ , и географические координаты пунктов на Земле остаются без изменений.
Моменты сил притяжения, которые действуют на экваториальные вздутия, меняются в зависимости от изменения положения Луны и Солнца по отношению к Земле. Когда Луна и Солнце находятся в плоскости земного экватора, моменты сил исчезают, а когда склонения Луны и Солнца максимальны, достигают наибольшей величины. Вследствие таких колебаний моментов сил тяготения наблюдается нутация земной оси. Нутационное движение складывается из ряда небольших периодических колебаний. Главнейшее из них имеет период 18,6 года – период обращения лунных узлов (точек пересечения орбиты Луны с эклиптикой). Движение с этим периодом происходит по эллипсу. Большая ось эллипса перпендикулярна направлению прецессионного движения и равна 16,4” (рис. 4). Малая ось параллельна направлению прецессионного движения и равна 13,7”. Таким образом, ось вращения земли описывает на небесной сфере волнообразную траекторию, точки которой находятся на угловом расстоянии в среднем около 230 27’ от полюса эклиптики.
Помимо лунно-солнечной прецессии и нутации, ось вращения Земли изменяет свое положение также и относительно тела Земли. Это явление называется движением полюсов. Оно приводит к изменению координат пунктов на Земле.
КОЛЕБАНИЯ ЗЕМЛИ.
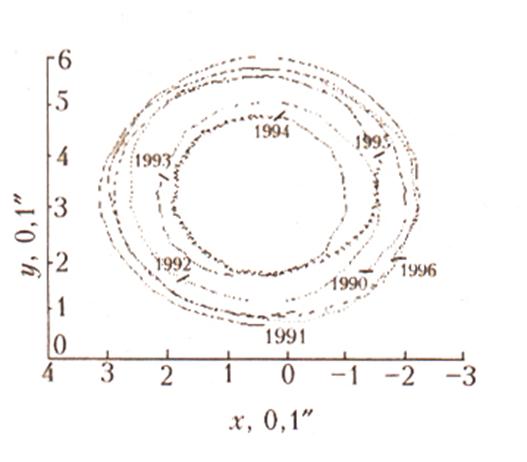
Происходящее в процессе ЭНЮК перераспределение воздушных и водных масс приводит к тому, что ось наибольшего момента инерции отклоняется по меридиану Австралии при Эль-Ниньо и по меридиану Таити при Ла-Нинья. Земля, являясь гироскопом, преобразует качания этой оси в движение оси наибольшего момента инерции Земли по конусу относительно оси суточного вращения. Из-за этого точки, в которых ось вращения пересекает земную поверхность – мгновенные полюсы Земли, - движутся. Они перемещаются по земной поверхности вокруг своего среднего положения в направлении вращения Земли, т.е. с запада на восток. Фигура, строение и физические свойства Земли таковы, что период свободных колебаний полюсов Земли равен 1,2 года. Помимо этого, чандлерова, движения полюсов имеется еще и вынужденное движение полюсов периодом 1 год. Сложение этих двух движений порождает биения, в результате которых радиус траектории полюса меняется от максимального до минимального с периодом примерно 6 лет ( рис. 5).
|
Рис. 5 Траектория движения Северного географического полюса Земли в 1990 – 1996
гг. с отметками начала каждого года.
Наибольшее удаление мгновенного полюса от среднего значения не превышает 15 м. (0,5”).
Движение полюсов порождает прилив в атмосфере и Мировом океане (полюсной прилив), амплитуда которого зависит от величины смещения полюса. Волна полюсного прилива движется в атмосфере и океане вслед за полюсами Земли и, несмотря на свою малость, приводит к синхронизации колебаний системы атмосфера – океан с циклами движения полюса. В результате в спектре ЭНЮК появляются гармоники с периодами, кратными чандлерову. Возникает явление комбинационного резонанса, при котором даже воздействия малой мощности способны возбудить наблюдаемое движение полюсов. Отсутствие в спектре ЭНЮК гармоник с периодами 1,2; 4,8; 7,2 года и т.д., вероятно, связано с явлением конкуренции – подавления одних гармоник другими в процессе их взаимодействия друг с другом.
Изменения интенсивности явления ЭНЮК во времени приводит к нестабильности процесса возбуждения чандлеровского движения полюсов, к изменению его характеристик (амплитуды, фазы, декремента затухания и т.д.). Например, в 1925 – 1945 гг. наблюдалось значительное затухание этого движения (в несколько раз уменьшилась его амплитуда, удлинился период и изменилась фаза). В этот же интервал времени имелись значительные аномалии в повторяемости теплых фаз ЭНЮК. Фазы с SOI < 0 стали возникать реже, а в период с 1930 по 1940 гг. длительных интервалов с SOI < 0 вообще не было. Около 1910 и 1955 гг. наблюдались максимальные амплитуды чандлерова движения полюсов. За 10 – 15 лет до этих моментов фазы SOI < 0 были наиболее длительными, интенсивными и, главное, кратными периоду Чандлера. Эти факты демонстрируют согласованность ЭНЮК с движением географических полюсов, т.е. с колебаниями оси Земли относительно оси суточного вращения.
Цикличность ЭНЮК тесно связана с цикличностью скорости вращения Земли. Механизм связи такой. В результате повышения температуры поверхности океана и выделения скрытого тепла конденсации при явлении Эль-Ниньо экваториальная тропосфера разогревается, увеличиваются разности температур между экватором и полюсами, что приводит к усилению западных ветров, к росту момента импульса атмосферы и как следствие к замедлению скорости вращения Земли (момент импульса системы атмосфера - Земля должен сохраняться). Во время Ла-Нинья аномалии температуры поверхности океана вдоль большей части экватора отрицательны, скрытого тепла выделяется меньше и температура экваториальной тропосферы понижается. Ослабевает контраст температуры между экватором и полюсами, падает сила западных ветров, момент импульса атмосферы уменьшается, и скорость вращения Земли увеличивается. Так как фазы ЭНЮК повторяются чаще всего через 6; 3,6; и 2,4 года, то в итоге имеет место аналогичная цикличность изменения скорости вращения Земли.
ВЛИЯНИЕ КОСМОСА НА КОЛЕБАНИЯ ЗЕМЛИ.
Резонансы вблизи периода Чандлера и его субгармоник свойственны не только системе Земля – атмосфера – океан, но и Солнечной системе. В Солнечной системе многие планеты, Луна и астероиды имеют периоды движения, соизмеримые с чандлеровским и шестилетним. Так, периоды обращения Юпитера, Сатурна, Урана и Плутона соответственно ровно в 10, 25, 70 и 207 раз больше периода Чандлера. Известно также, что узлы лунной орбиты непрерывно перемещаются по эклиптике к западу, совершая полный оборот за 18,6 г. Перигей же лунной орбиты движется к востоку, совершая оборот за 8,85 г. В результате такого встречного движения соединения узла с перигеем происходят ровно через 6 лет (nk = 5). Все это говорит о том, что за миллиарды лет эволюции Солнечной системы скорость суточного вращения Земли и процессы, происходящие на ней, синхронизировались с циклами Солнечной системы.
ЭКОЛОГИЧЕСКИЕ И ЭКОНОМИЧЕСКИЕ ПОСЛЕДСТВИЯ.
При Ла-Нинья пассатные ветры гонят поверхностную воду от берегов Америки к западу. Сгон сопровождается апвелингом – подъемом глубинной холодной воды. Она очень богата кислородом и питательными веществами – пищей планктона. Планктон является кормовой базой для рыб, поэтому у Тихоокеанского побережья Южной Америки откармливаются и быстро размножаются многочисленные стада рыб и связанные с ними пищевыми цепочками поголовья морских животных и стаи птиц.
Накопление же теплой, бедной кислородом воды у побережья Южной Америки при Эль-Ниньо подавляет апвелинг и вынос питательных веществ в верхние слои океана. Условия для развития планктона становятся неблагоприятными. Изменения гидрологических условий и первичной продуктивности океана приводит к миграции или мору обитающих там популяций рыб, ракообразных и морских животных. Птицы, питающиеся рыбой, также мигрируют или гибнут. Эль-Ниньо является катастрофой для многих морских экосистем. Требуются годы для преодоления негативных экологических последствий Эль-Ниньо.
Распределение температуры поверхности океана определяет расположение областей атмосферной конвекции над океаном в тропиках. При Ла-Нинья конвективная активность развита над Индонезией, Австралией и прилегающей западной частью Тихого океана и подавлена в восточной части, прилегающей к Южной Америке, где из-за охлаждения воздуха холодной водой океана существует пассатная инверсия, т.е. повышение температуры воздуха с высотой вместо обычно наблюдаемого падения. В западной тропической части Тихого океана идут обильные дожди, а в восточной стоит очень сухая погода. При Эль-Ниньо, когда аномалии температуры поверхности океана в восточной части становятся положительными, задерживающее влияние пассатной инверсии на вертикальные движение воздуха ослабевает и конвективная активность растет. Область повышенной конвективной активности с обильными осадками перемещается вместе с теплой водой вдоль экватора из западной в центральную и восточную части Тихого океана.
Миграция областей повышенной конвективной активности в атмосфере имеет далеко идущие последствия. При Эль-Ниньо в окрестностях Австралийско-Индонезийского центра действия, где обычно стоит влажная погода с дождями, наступает очень сухой период. В центральных и восточных же частях Тихого океана, где обычно дождей не бывает, наступает влажный период. Над прибрежными районами Южной Америки начинают идти проливные дожди. Они вызывают наводнения, оползни, уничтожают посевы, разрушают дороги и строения.
Таким образом, при Эль-Ниньо, которое может длиться несколько лет, в экваториальной зоне Тихого океана наступает подлинное экологическое бедствие: мигрируют или гибнут популяции рыб, ракообразных, морских животных, стаи птиц, страдает население прибрежных стран Южной Америки (особенно Эквадора и Перу), занимающиеся рыболовством и сбором ценного птичьего помета – гуано. Большой экономический ущерб этим странам наносят также и сопутствующие стихийные бедствия (наводнения, шквалы, грозы и т.д.). В этот же период экономика Австралии, Африки, Индонезии и стран бассейна Индийского океана страдает от сильных засух. Дефицит осадков, наблюдавшийся в годы Эль-Ниньо в большей части Восточного полушария, приводит к заметному понижению мирового урожая зерновых культур, поскольку большая часть посевных площадей находится в Восточном полушарии. Чем сильнее эль-Ниньо, тем тяжелее описанные последствия. По неполным данным, Эль-Ниньо 1982 –1983 гг. привело к гибели более 2 тыс. человек, а ущерб составил 13 млрд. долларов.
На основании проведенного анализа зависимости явления ЭНЮК от колебаний системы Космос – Земля –атмосфера – океан мы можем сделать вывод, что многие катастрофы и природные катаклизмы, происходящие на нашей планете имеют первопричиной не деятельность «высших сил», ведущих Землю к «концу света». Их причины более прозаично связаны с периодическими колебаниями физических систем и воздействием на них сторонних сил, имеющих также физическую природу.
Итак, природные катаклизмы вызываются периодическими колебаниями системы атмосфера – океан – Земля под воздействием Солнца (прецессия), неравномерности прогрева атмосферы (воздействие воздушных масс на Землю), неравномерным прогревом океана (океанические течения воздействуют на Землю). В результате этого ось Земли прецессирует и нутирует, что приводит к приливам в атмосфере и океане. Если этот прилив совпадает с движением масс, вызванных неравномерным прогревом, то на Земле возникают ураганы, наводнения. Если приливы, вызванные движением полюсов Земли направлены против воздушных масс и океанических вод, то получается минимум стихийных бедствий и катаклизмов.
Так как система Космос – Солнце – атмосфера – океан – Земля существует миллиарды лет, то наблюдается устойчивая картина чередования этих воздействий, т.е. периодичность природных катаклизмов.
Надо еще учитывать направление вращения магмы внутри Земли. При изменении оси вращения Земли изменяется и направление вращения магмы, которое в свою очередь воздействуют на биения направления оси Земли.
Углубленный анализ явлений природы (в том числе и катастрофических) вскрывает их суть и не оставляет камня на камне от «теорий» приближающегося «конца света».
ПРИЧИНЫ РАЗБРОСА ЗНАЧЕНИЙ ПЕРИОДА
ПОВТОРЕНИЯ КАТАКЛИЗМОВ.
Разброс значений периода повторения катаклизмов на Земле вызывает большую неудовлетворенность ученых, так как невозможно предсказать на большой промежуток времени время наступления стихийных бедствий. Этот вопрос решался с 1984 года с применением сверхмощных компьютеров, и в результате установили, что разброс значений периода повторения катаклизмов обусловлен хаотическим поведением орбит планет Солнечной системы, т.е. планеты движутся не по стационарным орбитам, как предполагал Лаплас в 18 веке и как трактует даже современная астрономия.
Тела Солнечной системы, имея определенный период обращения, воздействуют друг на друга. Это было известно еще во времена Ньютона. Но современные исследования математиков Колмогорова (Россия), Арнольда и Мозера (США) показали, что между планетами Солнечной системы в определенный момент возникает резонансное взаимодействие, которое и выводит Солнечную систему из квазипериодического движения.
Рассчитать период повторения резонансного взаимодействия на длительный срок очень сложно. Это же невозможно сделать и при попытке расчета назад во времени. Но точно установлено, что все тела Солнечной системы совершают квазипериодические движения и находятся в зоне относительной устойчивости через определенный промежуток времени, значение которого непостоянно в связи с резонансом.
А вот установление математической зависимости периода относительной устойчивости орбит тел Солнечной системы не под силу даже современным ЭВМ, т.к. в любой момент времени изменяются начальные условия этого процесса (например, появляются несколько комет из облака Оорта). В облаке 150 млрд. комет, которые образовались вместе с планетами и до сих пор идет процесс образования новых комет. Потребуются еще годы исследований, чтобы понять хаотическое движение тел Солнечной системы и рассчитать зависимость периода повторения квазиустойчивых состояний и катаклизмов.
В продолжении моей работы о причинах природных катаклизмов и рассмотрены работа Пуанкаре «Новые методы небесной механики», работы Колмогорова, Арнольда и Мозера (КАМ), результаты исследования космических зондов «Вояджер», «Пионер»(США), проекта «ВеГа» (Венера – комета Галлея)(Россия) и результаты обработки полученных данных с помощью суперкомпьютера NASA, который рассчитал орбиты планет на 900 млн. лет вперед, но без учета резонанса, что и приведет к 100% ошибке через 100 млн. лет.
НЕВОЗМОЖНОСТЬ ПРИМЕНЕНИЯ ЗАКОНОВ
НЬЮТОНА ПРИ РЕШЕНИИ ЗАДАЧИ ВЗАИМОДЕЙСТВИЯ ТЕЛ СОЛНЕЧНОЙ СИСТЕМЫ.
Небесная механика изучает движение тел Солнечной системы под воздействием сил тяготения. Законы Ньютона и закон всемирного тяготения позволяют прекрасно смоделировать движение этих тел (правда, для близких к Солнцу планет необходимо учитывать поправки, связанные с законами общей теории относительности, - современной теории тяготения; для комет важны также поправки на негравитационные силы). Второй закон Ньютона устанавливает соотношение между ускорениями тел и их координатами. Поведение системы задается начальными условиями, т.е. значениями ее N координат и N скоростей в определенный момент времени. Число N называется числом степеней свободы системы. Например, движение маятника – это движение системы с одной степенью свободы, т.к. его можно описать задав угол, который образует нить маятника с вертикальной осью и угловую скорость.
Законы Ньютона не позволяют непосредственно решить задачу N тел, т.е. найти формулу, определяющую их положения и скорости в любой момент времени по заданным координатам и скоростям в начальный момент времени. Точно так же нам неизвестно, как изменяются траектории тел при небольшом изменении начальных условий. Ведь точные начальные условия задает только математик – он сам и задает их при решении задачи. Астроном лишь приблизительно определяет положения и скорости тел Солнечной системы, используя целый арсенал достаточно несовершенных инструментов (телескопы, космические зонды, лазеры, радиолокаторы, кинокамеры и т.д.). Эта неустранимая неточность измерений заставляет астронома изучать траектории планет, заведомо задавая начальные условия с некоторой ошибкой. Сравнить результаты с точным расчетом можно в одном-единственном случае – в задаче двух тел, или задаче Кеплера. Только в этом случае с помощью законов Ньютона можно получить общую формулу, определяющую траекторию планеты (или любого другого объекта), обращающейся вокруг Солнца. Траектории в задаче двух тел могут быть эллипсами, гиперболами или параболами. Если наблюдаемые траектории отличаются хоть в малой степени от кеплеровских, то дальнейший расчет поведения тел, движущихся по ним, становится очень трудной задачей.
РЕШЕНИЕ ЗАДАЧ ВЗАИМОДЕЙСТВИЙ ТЕЛ
СОЛНЕЧНОЙ СИСТЕМЫ МЕТОДОМ ТЕОРИИ ВОЗМУЩЕНИЯ.
Перед рассмотрением метода теории возмущения следует вспомнить некоторые характеристики движения планет. Прежде всего, в этом случае сохраняется полная энергия планеты. Системы такого типа называются консервативными. Энергия консервативной системы является функцией координат и импульсов тел, входящих в ее состав. Для консервативных систем можно записать уравнения движения, эквивалентные уравнениям Ньютона, - уравнения Гамильтона, в которых в качестве переменных используются координаты и импульсы, а не координаты и скорости.
При выборе соответствующих переменных, называемых каноническими, эти уравнения принимают очень симметричную форму относительно координат и импульсов тел. Это не помогает их решить, но облегчает изучение общих свойств решений. В случае интегрируемых систем уравнений можно найти такую новую систему независимых переменных (нормальные координаты), в которой уравнения Гамильтона становятся очень простыми. При этом движение сводится к сложению периодических круговых движений, характеризуемых собственными частотами. Записанное в таких переменных движение называется квазипериодическим. Фазовые траектории интегрируемой системы заполняют поверхность тора. В результате анализа подобных систем получают формулу, позволяющую рассчитать положение тел в любой момент времени в прошлом или будущем, исходя из заданных начальных условий.
К сожалению, большинство динамических систем относится к классу неинтегрируемых ( по существу, интегрируемыми являются только системы с одной степенью свободы – вроде маятника), поэтому не удается найти преобразование от обычных координат к нормальным и упростить задачу. Однако в небесной механике системы во многих случаях близки к интегрируемым. Так, если пренебречь взаимодействием между планетами, то система планет, движущихся в поле Солнца, становится, с точки зрения математики, интегрируемой, так как движение каждой планеты не зависит от движения другой и может быть точно определено из решения задачи Кеплера.
Массы планет очень малы по сравнению с массой Солнца, поэтому их гравитационное взаимодействие друг с другом много меньше их гравитационного взаимодействия с Солнцем. Этот малый параметр пропорционален отношению массы планеты к массе Солнца.
Астрономы и математики, начиная с Лагранжа и Лапласа (XVIII в.), разработали метод, позволяющий найти приближенное решение уравнений, содержащих малый параметр. Это метод теории возмущений, когда решение задачи ищется в виде ряда по степеням малого параметра.
Суть заключается в том, что сначала отбрасываются все слагаемые, связанные с отклонением системы от интегрируемой. Тогда можно найти точное решение получившейся задачи, как говорят, в нулевом приближении. Затем учитывается главная поправка, пропорциональная первой степени малого параметра e (первый порядок теории возмущений), затем следующая поправка, пропорциональная e2 (второй порядок теории возмущений) и т.д. На практике расчеты очень быстро становятся настолько сложными, что остается только ограничиться первыми поправками, аргументируя отбрасывание всех последующих тем, что их вклад пропорционален высокой степени малого параметра e <<1. Решения, получаемые таким способом, также являются квазипериодическими функциями.
МЕТОД ПУАНКАРЕ И ТЕОРИЯ КАМ.
Незадолго до Французской революции Лаплас и, независимо, Лагранж, ограничиваясь вычислениями в первом порядке теории возмущений, показали, что движение планет в Солнечной системе является квазипериодическим. Это указывает на ее стабильность: длины полуосей, эксетриситет и угол наклона к плоскости эклиптики планет испытывают только малые отклонения от средних значений. Заменой переменных можно свести движение планеты к квазипериодическому движению на торе. Чтобы на долгое время вперед узнать, как будет эволюционировать Солнечная система, необходимо знать частоты квазипериодических движений. Уточнив расчеты Лагранжа и Лапласа, Леверье в 1856 г. учел отброшенные ими поправки и получил совершенно другие значения основных частот движений планет. Леверье надеялся, что по крайней мере для внешних планет (Юпитера, Сатурна, Урана), массы которых хорошо известны благодаря наблюдениям движений спутников этих планет, реальные значения частот окажутся близкими к вычисленным.
Однако последующие расчеты в еще более высоком порядке теории возмущений, выполненные в 1897 г. Хиллом, показали, что и Леверье был не прав. Сохраняя все больше членов разложения, мы получаем новые частоты, сильно отличающиеся от прежних. В таком случае говорят, что ряд теории возмущения не сходится.
Анализ всей проблемы заново провел Пуанкаре. В трехтомном труде «Новые методы небесной механики», опубликованном в 1892 – 1897 гг., он показал, что задача трех тел, движущихся впод действием сил взаимного тяготения, не интегрируется (т.е. не может быть решена аналитически). Пуанкаре доказал, что безусловно, можно искать решение в виде ряда теории возмущений, но все равно ряд не может описать реальное движение планет. Оказывается, получаемые ряды являются, как говорят математики, асимптотическими. Свойство таких рядов заключается в том, что учет первых нескольких членов приводит к сходящемуся результату (каждая следующая поправка меньше предыдущей), однако сумма ряда расходится. Решения, получаемые обрыванием асимптотических рядов, могут с хорошей точностью описать поведение системы на конечном отрезке времени, однако оказываются совершенно непригодными при анализе устойчивости системы за большой промежуток времени.
Совсем недавно, в 60-х гг. нашего столетия, была создана теория КАМ (по именам выдающихся современных математиков Колмогорова, Арнольда и Мозера), позволившая уточнить результаты Пуанкаре. Метод теории возмущений заключается в поиске таких замен переменных, которые позволяют привести систему к интегрируемой и искать малые отклонения от нее, т.е. свести движение к суперпозиции (почти) равномерных движений по окружностям. Теория КАМ показывает, что при некоторых начальных условиях общее движение действительно является квазипериодическим, как и в случае интегрируемых систем. Однако при других значениях начальных условий появляются области неустойчивости (области хаотического движения), в которых происходят значительно более сложные явления, и методы теории возмущений оказываются неприменимыми. Чем меньше параметр e, тем ближе движение к квазипериодическому и тем меньше области неустойчивости. В этом случае теория возмущений хорошо работает, приводя к приближенным результатам, очень близким к реальности.
В случае систем с двумя степенями свободы Пуанкаре предложил очень полезный метод, позволяющий отличить квазипериодическую траекторию от хаотической. Вместо того, чтобы изучать саму траекторию в фазовом пространстве, изучают последовательные пересечения этой траектории с должным образом выбранной плоскостью (или – в общем случае – с поверхностью).
Что же такое фазовая траектория? Рассмотрим для определенности одномерный гармонический осциллятор – колебательную систему, образом которой может служить груз на горизонтальной плоскости без трения, соединенный с упругой пружиной жесткостью k. Груз совершает колебания по закону:
X = Acos(wt + j), следовательно, скорость груза V= - Awsin(wt + j) и импульс p = - mAwsin(wt + j). Как известно, упругая потенциальная энергия сжатой пружины U = kX2 /2. Полная энергия груза равна E=mV2 /2 + kX2 /2 = p2 /(2m) + kX2 /2. Если на плоскости построить график зависимости импульса груза p от координаты х, это и будет фазовая траектория. Благодаря закону сохранения энергии в случае одномерного движения задача определения формы фазовой траектории решается просто, так как формулу закона сохранения энергии можно переписать в виде:
![]()
Это есть уравнение эллипса на плоскости (р,х). Каждому значению энергии Е, определяемому начальными условиями, отвечает единственная фазовая траектория осциллятора.
Чтобы изучить фазовую траекторию системы с двумя степенями свободы (размерность фазового пространства равна тогда 4), следует рассмотреть сечения фазового пространства должным образом выбранной плоскостью А, отвечающей фиксированному моменту времени. В результате получается сечение Пуанкаре. В некоторых случаях удается точно найти преобразование координат плоскости, позволяющее переходить от одного сечения к другому. Существует стандартный вид такого преобразования, задаваемого формулами:
![]()
x’ = x + asin(x + y),
y’ = x + y
где подразумевается, что штрихованные координаты вычислены по модулю 2p.
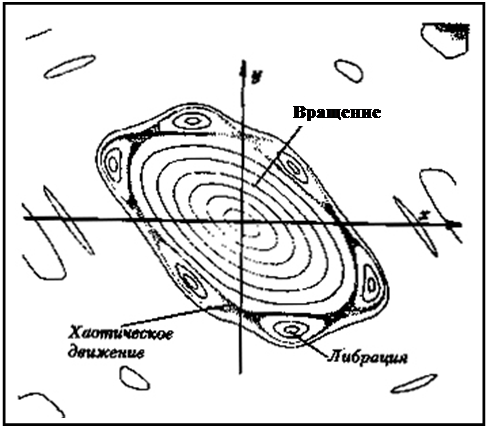
Иногда удается найти преобразование переменных, позволяющее переходить от одной точки в фазовом пространстве к другой. В этом случае можно изучить поведение системы за длительный период времени, используя ЭВМ. Простой пример таких преобразований показан на рис.6, где в сильно упрощенном виде показаны разные типы возможных траекторий.

|
|||
|
В центре графика показаны орбиты, отвечающие малым значениям параметра возмущения; они представляют собой замкнутые гладкие кривые. Во внешней области появляются шесть областей устойчивости, внутри которых структура похожа на ту, которая имеется в центре. Вокруг каждого из островов устойчивости существует область неустойчивости, хаотическая зона. Она соответствует области колебания маятника вблизи границы, где движения сильно зависят от начальных условий и могут быть очень нестабильны. Приведенный рисунок получен в результате численного моделирования на ЭВМ и полностью согласуется с результатами теорий Пуанкаре и КАМ. Рисунок тем и замечателен, что он был теоретически описан математиками еще до появления ЭВМ.
ГИПЕРИОН И ПОЯС АСТЕРОИДОВ КАК ИЛЛЮСТРАЦИЯ ХАОТИЧЕСКОГО ДВИЖЕНИЯ. РЕЗОНАНСЫ В ДВИЖЕНИИ НЕБЕСНЫХ ТЕЛ.
Теоретическое существование хаотических режимов движения в системах, подчиняющихся законам небесной механики, совсем не означает, что эти режимы должны обязательно наблюдаться. Их можно наблюдать только в том случае, если орбитальные параметры каких-то тел Солнечной системы существенно меняются за время, много меньшее возраста самой этой системы.
Одним из первых примеров можно взять поведение Гипериона, спутника Сатурна, фотографии которого были получены в 1981 г. космическим зондом «Вояджер-2». Гиперион представляет собой бесформенную глыбу, длина которой вдвое больше ширины (самый малый поперечный размер 200 км.). Хаотическая форма Гипериона объясняется существованием области неустойчивости при движении в системе Гиперион – Титан – Сатурн, да и сам Гиперион хаотично вращается вокруг своей оси.
Сечение Пуанкаре траектории Гипериона, рассчитанное на ЭВМ, соответствует стационарной орбите, возникающей в результате резонанса движений двух спутников Сатурна – Титана и Гипериона (резонансом в данном случае является такое движение спутников вокруг планеты, когда время обращения одного кратно времени обращения другого). Однако, если начальные условия совсем немного отличаются от тех, которые соответствуют этой орбите, траектории попадают в зону неустойчивости. Тело, помещенное на неустойчивую орбиту, будет рано или поздно выброшено из системы Сатурн – Титан – Гиперион при сближении с Титаном. Итак, теперь можно дать объяснение бесформенности Гипериона. За время своего существования Гиперион испытал многократные столкновения со сравнительно небольшими телами, обильно населяющими окрестности Сатурна. Куски Гипериона, которые были отколоты в результате таких ударов, собрались вокруг него под действием сил гравитации в гигантское облако. Однако благодаря наличию зоны неустойчивости вблизи орбиты Гипериона, эти осколки не упали обратно на Гиперион, а были постепенно (за время, много меньшее времени жизни самого Гипериона) выброшены из системы Сатурн – Титан – Гиперион в окружающее пространство.
Есть и другой тип неустойчивости при движении тел в Солнечной системе. Большинство спутников планет и даже одна из планет (Меркурий) совершают движения, жестко определяющиеся резонансом между вращением вокруг оси и обращением вокруг планеты или Солнца: за время полного оборота по орбите они обращаются вокруг своей оси целое число раз. Именно по этой причине Луна повернута к нам всегда одной стороной. Она вращается вокруг своей оси с тем же периодом, что и период ее вращения по орбите вокруг Земли (резонанс 1:1). Такое синхронное вращение установилось постепенно, за время порядка времени существования Солнечной системы. Физическая причина этой резонансной настройки двух вращений – приливные гравитационные силы, постепенно тормозящия вращение Луны вокруг своей оси и меняющиеся с периодом, равным периоду обращения Луны вокруг Земли.
Как было показано в 1984 г., Гиперион близок как к этому резонансному состоянию (1:1), так и к резонансному состоянию 3:2. Российский физик Б.Чириков показал, что в такой ситуации, когда динамическая система пытается установить согласие между двумя резонансными состояниями, возникает неустойчивость. Действительно, недавние наблюдения подтверждают, что направление оси вращения и угловая скорость Гипериона изменяются случайным образом на протяжении времени в несколько периодов обращения по орбите (21 день).
Итак, движение Гипериона представляет собой единственный известный в Солнечной системе пример быстрого хаотического поведения. На самом деле, как показал Дж.Уисдом, все спутники иррегулярной формы на протяжении своей эволюции попадали в область неустойчивости и совершали хаотические движения, когда ни находились в такой точке орбиты, в которой возможен захват в резонансное состояние.
Динамика хаоса играет важную роль в эволюции движения других малых тел Солнечной системы: астероидов и комет. Их движение было по-настоящему изучено только в последние десятилетия, когда появились соответствующие наблюдательные средства, позволившие прежде всего очень точно определять параметры орбит малых тел. Эти исследования привели к лучшему пониманию процесса формирования планет. На самом деле малые тела являются неиспользованными во время «строительных работ» «кирпичиками». В этом плане особенно показательны астероиды. По современным теориям, в результате слипания газа и пыли первичных межзвездных облаков между орбитами Марса и Юпитера образовались сгустки линейными размерами порядка 100 км., двигавшиеся по почти круговым орбитам с очень близкими скоростями. Казалось бы, есть все условия для последующего слипания этих сгустков в крупную планету. Однако под влиянием тяготения Юпитера в эту зону вбрасывались другие сгустки, которые, как шар при игре в кегли, оказывали разрушающее воздействие.
В результате, как теоретически показано в модели В.Сафонова, все осколки должны были образовать диск в области пояса астероидов на расстоянии порядка 2,5 а.е. Поскольку соударения сгустков в этой модели предполагались случайными, распределение орбит астероидов в диске должно быть равномерным. Однако анализ известных орбит показывает, что это не так. В главном, сильно населенном поясе астероидов ( на расстоянии 2 – 3 а.е. от Солнца) существуют узкие зоны (лакуны Кирквуда), в которых не обнаружено практически ни одного астероида. Эти зоны соседствуют с достаточно населенными областями, в которых наблюдаются семейства астероидов. С другой стороны, внешняя зона астероидов (от 3,3 до 5,2 а.е., т.е. до орбиты Юпитера) практически пуста, за исключением нескольких очень компактных групп этих тел. Если для каждой наблюдаемой орбиты вычислить период обращения астероида по ней, то обнаруживается замечательное явление. Все аномальные распределения орбит соответствуют резонансной ситуации, когда отношение периода вращения астероида к периоду вращения Юпитера равно 1:1; 1:2; 1:3 и т.д.
Самым загадочным в поведении астероидов является существование лакун Кирквуда. Для объяснения этого факта предлагались различные гипотезы. Уравнения движения астероида под действием сил притяжения со стороны Солнца и Юпитера являются нелинейными и неинтегрируемыми. Возникает соблазнительная идея отнести наблюдаемые лакуны на счет неустойчивостей, почти всегда присутствующих вблизи резонанса. Однако действительность оказывается сложнее: существование компактных групп астероидов во внешнем поясе подтверждает, что в некоторых резонансных ситуациях астероиды все же могут устойчиво находиться.
Прорыв в понимании проблемы стал возможен после замечательного открытия Б.Чирикова, связанного с исследованием динамики частиц в ускорителях. Воспользовавшись результатами Чирикова, Дж.Уисдом в 1983 г. сумел смоделировать влияние Юпитера, заменив его постоянное тяготение серией отдельных импульсов, действующих на астероид в определенных местах орбиты в течение определенного времени. В этом случае задачу о влиянии одного импульса удается решить аналитически, после чего можно рассчитать и всю орбиту. Уисдом доказал, что орбиты, близкие к резонансу 3:1, неустойчивы и меняются очень своеобразно. В течение десятков или даже сотен тысяч лет орбита с умеренным эксцентриситетом не меняется. Затем внезапно эксцентриситет быстро растет от значения 0,1 до 0,4, после чего опять уменьшается. Такие всплески эксцентриситета повторяются случайным образом.
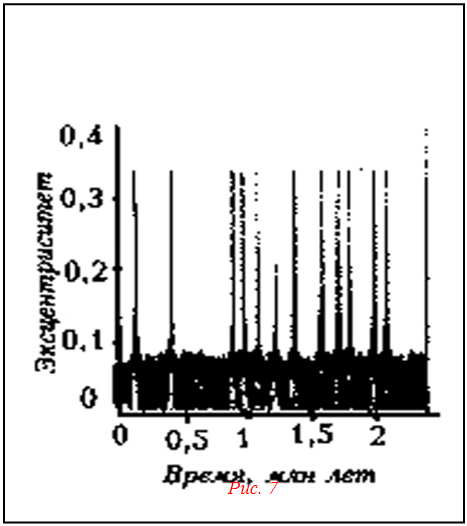
На рисунке 7 изображены результаты численного моделирования эволюции орбиты астероида, отвечающей резонансу 1:3. Они демонстрируют, что на протяжении миллионов лет возникают сильные прерывистые всплески значений эксцентриситета орбиты. В период такого всплеска астероид может пересечь орбиту Марса и под влиянием тяготения этой планеты оказаться выброшенным из устойчивой зоны, превратившись в астероид-бродягу. Благодаря этому возможно образование лакун в распределении орбит астероидов.
НЕУСТОЙЧИВОСТЬ В ДВИЖЕНИИ КОМЕТ.
Возмущения, вызываемые наличием планет, сильно влияют и на движение комет. В частности, последнее прохождение кометы Галлея в 1985 г. вызвало появление многочисленных работ по динамике движения комет с большим эксцентриситетом орбит. Предсказания появление кометы Галлея всегда были вызовом астрономам, с того самого момента, когда Эдмунд Галлей предсказал в 1705 г., что комета вернется примерно через 75 лет. Действительно, с тех пор появления кометы были регулярными с периодом 75-80 лет, но точное значение периода зависит от возмущающего действия на орбиту кометы со стороны планет, оказывающихся поблизости в данное время.
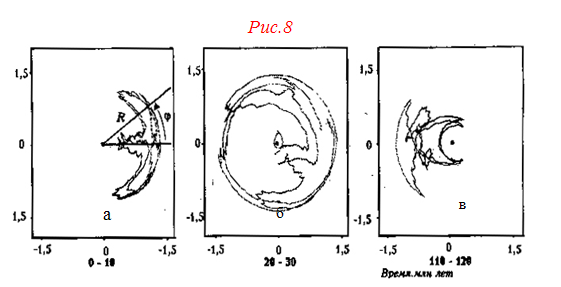
По случаю последнего появления кометы были сделаны новые расчеты ее орбиты с использованием всей мощи современной вычислительной техники. Их точность составляла один год по шкале времени. Выяснилось, что расчеты очень хорошо совпадают с предшествующими наблюдениями появления кометы вплоть до 1403 г. с периодом 86 лет. Однако историкам астрономии удалось датировать появления кометы Галлея, начиная с 163 г. И тут выяснилось, что этот момент времени как раз соответствует границе зоны неустойчивости. Если расхождение расчетов и наблюдений на промежутке времени в 615 лет, считая от 163 г., равно всего двумстам дням, то за последующие семьсот лет – до 1403 г. – увеличивается до пяти лет. Все эти особенности движения кометы Галлея нашли свое объяснение в том, что эти движения неустойчивы. В рамках простой модели, в которой влияние Юпитера описано короткими импульсами в моменты прохождения кометы, было показано, что орбита кометы Галлея соответствует сепаратиссе на рисунке 8б.
Комета Галлея – рядовая комета Солнечной системы. Во всех случаях проблема одна и та же: кометы «смертны». Это означает, что в результате развития неустойчивости орбиты комета может быть рано или поздно выброшена за пределы Солнечной системы.
Но мы тем не менее все время наблюдаем кометы. Следовательно, существует какой-то источник новых комет у границ солнечной системы – облако пыли, скопление осколков за орбитой Нептуна и т.п. Расчеты позволяют представить себе сложный механизм передачи массы: астероиды, беспорядочно меняющие свои орбиты под действием внутренних планет и выбрасываемые за пределы Солнечной системы, заменяются вторгшимися из дальних областей кометами, которые могут превратиться в астероиды, и т.д.
НЕУСТОЙЧИВОСТЬ В ДВИЖЕНИИ ПЛАНЕТ СОЛНЕЧНОЙ СИСТЕМЫ.
Какие выводы мы можем сделать из всего сказанного? Какова возможная судьба планет Солнечной системы? Движение планет часто используют в качестве примера периодического регулярного движения. Эту регулярность мы ощущаем в повседневной жизни, наблюдая смену времен года, затмения в полном согласии с расчетами, и т.п.
Тот простой факт, что мы существуем, исключает возможность, что за последние миллионы лет Земля испытала сильные колебания орбиты, так как это должно было полностью изменить климатические условия, что не могло остаться незамеченным. Но было ли так всегда? Даже после доказательства хаотического движения ряда астероидов все еще бытует точка зрения, что движение планет было устойчивым все последние 5 млрд. лет с момента образования Солнечной системы. И действительно, все численные расчеты, проведенные до 1984 года, показывали устойчивость орбит планет (особенно внешних – Юпитера, Сатурна, Урана, Нептуна, Плутона) за интервалами времени до нескольких десятков миллионов лет. Эти расчеты только укрепили представления о квазипериодическом характере движения планет в духе идей Лапласа.
Однако использование новых сверхмощных ЭВМ позволило в 1984 году осуществить расчеты орбиты Плутона на период времени 845 млн.лет. Было доказано, что орбита Плутона нестабильна, и небольшое изменение начальных условий приводит к тому, что расстояние, разделяющее две близкие в какой-то момент времени орбиты, возрастает вдвое через 20 млн. лет, что делает невозможным любое предсказание движения Плутона на период времени свыше 400 млн. лет. Несмотря на этот результат, считалось, что другие планеты движутся по устойчивым орбитам, так как неустойчивость орбиты Плутона казалась связанной с его аномально низкой массой (около 1/100000 массы Солнца).
В 1988 г. удалось провести аналогичные расчеты для внутренних планет. Сложность заключалась в том, что прямое численное интегрирование уравнений движения этих планет на больших промежутках времени недоступно даже лучшим ЭВМ из-за слишком быстрого движения этих планет по орбите и, следовательно, слишком быстрого «ухода» от начальных условий. Сначала следовало как-то преобразовать исходные уравнения, используя методы теории возмущений. В результате система уравнений Ньютона для совокупности планет преобразовалась в систему из 150000 уравнений, описывающую не точное движение планет, а среднее значение их положений на орбите. С помощью суперкомпьютера НАСА за 6 ч. работы удалось рассчитать орбиты планет на 900 млн. лет вперед. Результат получился удивительным: если для больших планет движение оказалось регулярным, то для внутренних планет – Меркурия, Венеры, Земли и Марса – поведение траекторий неустойчиво. Расчеты показывают, что расстояние между двумя изначально близкими орбитами этих планет увеличивается втрое каждые 5 млн. лет, поэтому невозможны никакие точные предсказания их орбит на период свыше 100 млн. лет. Ошибка всего в 0,00000001% в начальных условиях приводит через 10 млн. лет к относительному расхождению орбит в 0,0000001%, но становится 100-процентной через 100 млн.лет!
Как и у других малых тел, динамика планет неустойчива, однако результаты этой неустойчивости проявляются только в масштабах времени свыше 10 млн. лет. В представленных на рисунках 8 траекториях Земли и Марса, полученных численными методами, мы прослеживаем хаотичность их движения. На графиках показано изменение угла j , представляющего комбинацию прецессии орбит Земли и Марса, как функцию расстояния R от Солнца (поведение расстояний такое же, как у эксцентриситета орбиты). Каждый рисунок представляет эволюцию траектории в течение 10 млн. лет после определенного срока в прошлом: а) в течение первых 10 млн. лет колебания угла j происходят в ограниченном интервале значений, как у малых колебаний маятника; б) в течении интервала между 20 и 30 млн. лет после начала движение переходит во вращение, так что угол меняется почти на 2p ; в) в интервале от 110 до 120 млн. лет движение представляет собой либрацию, но в окрестности совсем другой точки. Таким образом, предсказание поведения орбит планет на срок более 100 млн. лет оказывается невозможным, так как малые изменения начальных условий приводят к случайным переходам орбит от одной зоны устойчивости к другой, полностью разрушая детерминированный ход событий.
ЗАКЛЮЧЕНИЕ.
Мы установили причину хаотического поведения орбит планет Солнечной системы и связанный с ней разброс значений периода повторения природных катаклизмов на Земле. Она связана с близостью реального движения этих планет к условиям резонанса между периодами их обращения. После работ Пуанкаре и последующих работ КАМ казалось, что лапласовский детерминизм подтвержден: Солнечная система совершает квазипериодические движения и находится в зоне относительной устойчивости. На самом деле резонансы между разнородными периодическими движениями разрушают ее, не позволяя дать предсказания об эволюции Солнечной системы на сколь-нибудь длительный срок. Это же невозможно сделать и при попытке расчета назад во времени. В связи с этим трудно сейчас судить, каким был в прошлом отклонения эксцентриситета Земли от теперешнего значения и как это могло повлиять на ее климат со всеми вытекающими последствиями для темпа и характера эволюции биомассы.
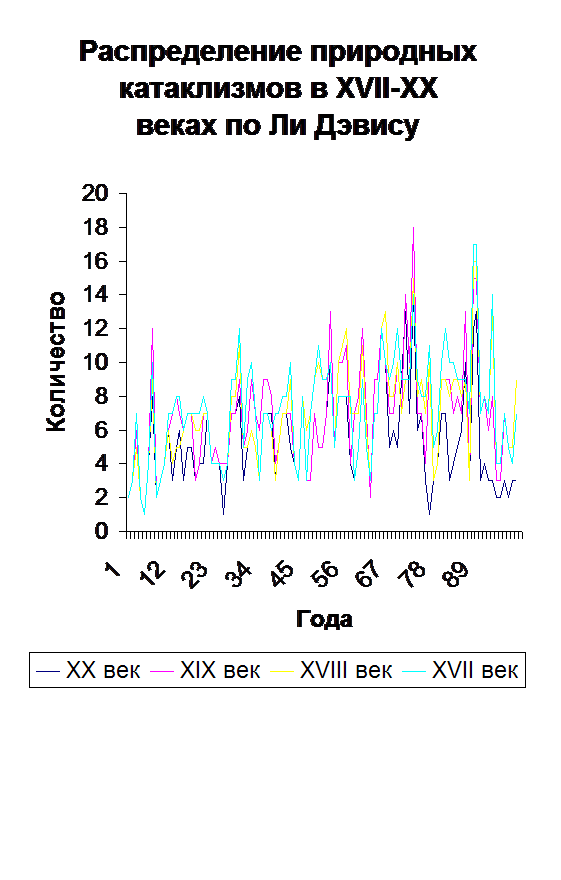
Однако простой количественный анализ трагических событий, проведенный крупным знатоком истории катастроф Ли Дэвисом, выявил некоторую «последовательность случайностей» (см. диаграмму). Она напоминает кардиограмму, на которой «сердцебиение» катастроф очень странно совпало в веках. Последняя треть каждого столетия действительно чревата всплесками, но в то же время на рубеже веков – в самом конце и в самом начале – никакого пика катастроф, «готовящих» конец света, нет.
СПИСОК ЛИТЕРАТУРЫ.
1. Н. С. Сидоренков. Характеристики явления Эль-Ниньо -
Южное колебание. – Труды
Гидрометцентра СССР, 1991 г., вып. 316,
Стр. 31 – 44.
2. Н. С. Сидоренков. Влияние Эль-Ниньо – Южного
колебания на возбуждение чандлерова
движения полюсов. – Астрономический
журнал, 1997 г., т.74, вып.5, с.792 – 795.
3. М. И. Рабинович, Д. И. Трубецков. Введение в теорию
колебаний и волн. М. Наука, 1991 г.,
с. 432.
4. Дж. Карери. Порядок и беспорядок в структуре
материи. М. Мир, 1985 с.51 – 55.
5. Р.В.Полозов Хаос в Солнечной системе.
«Физика» № 13 /1997 стр. 5 - 11
СОДЕРЖАНИЕ.
Введение………………………………………………………..1
Колебания атмосферы ………………………………………...3
Колебания океана ……………………………………………..6
Динамика вращающихся тел …………………………………8
Колебания Земли ………………………………………………11
Влияние Космоса на колебания Земли ……………………….13
Причины разброса значений периода
повторения катаклизмов………………………………………..16
Невозможность применения законов Ньютона при
решении задач взаимодействий тел Солнечной системы … 17
Решение задач взаимодействий тел Солнечной системы
методом теории возмущений ……………………………….18
Метод Пуанкаре и теория КАМ ……………………………….20
Гиперион и пояс астероидов как иллюстрация хаотического
движения. Резонансы в движении небесных тел …………….23
Неустойчивость в движении комет ………………………… 27
Неустойчивость в движении планет Солнечной системы… 28
Заключение …………………………………………………… 30
Список литературы …………………………………………….32