Реферат: Харакатхо
В А З О Р А Т И М А О Р И Ф И Ч У М Х У Р И И Т О Ч И К И Т О Н
У Н И В Е Р С И Т Е Т И Т Е Х Н И К И И Т О Ч И К И С Т О Н
Б А Н О М И А К А Д Е М И К М. О С И М И
КАФЕДРАИ ФИЗИКА
Лабораторияи механика, физикаи
малекулави ва термодинамики
ХИСОБОТИ
Кори лаборатории № 6
______________________________
______________________________
______________________________
|
Факултаи энергетики, курси II , гурухи "6547А" |
|||
Ном, номи падар |
Имзо |
Таърих |
|
Тахияи |
Умаров Нозим Чамшедович |
||
Санчид |
|||
| Химояро кабул кард |
ОМУХТАНИ КОНУНХОИ ХАРАКАТИ ЧАРХЗАНИ
ДАР РАККОСАКИ ОБЕРБЕК
Максади кор: санчиши тачрибавии муодилаи асосии инамикаи харакати чархзани ва муайяан кардани моменти инерцияи чисмхои сахт.
Лавозимот: раккосаки Обербек, штангенциркул, качмуйи борчахо.
Назарияи метод ва тафсири дастгох
Муодила асосии динамикаи харакати чархзании чисми сахт:
![]()
![]() M = Áع (1)
M = Áع (1)
Шабехи муодилаи асосии динамикаи харакати пешрави:
![]()
![]() F
= mα (2)
F
= mα (2)
![]() мебошад, ки дар он
М – момменти гардишовари кулли куввахои ба чисм таъсиркунанда, Á -моменти инерцияи
ин чисм нисбат ба мехвари чархзани, ع - шитоби кунчии
мебошад, ки дар он
М – момменти гардишовари кулли куввахои ба чисм таъсиркунанда, Á -моменти инерцияи
ин чисм нисбат ба мехвари чархзани, ع - шитоби кунчии
харакати чархзанист. Дастгохи ба
|
|
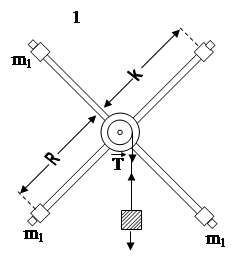
(таввасути шарикоподшипгик) чарз зада метавонад. Ба милозо борхои якандозаи массаашон m1 чуфт-чуфт дар сасофаи якхелаи муайян аз мехваи чархзани чойги ркарда, моменти инерцияи раккосакро тагйир додан имконпазир аст (расми 1).
Ба дискхо як нуги расмони дар нуги дигараш платформа (сахн)-и массааш малум овезнбударо андармону печонида мешавад. Бо таъсироти платформа ва борчахои дар он чойгирмекардаи массаашон муайян 10 (расми 2) расмони печонида кушода ва таввасути кувваи тарангии расмон (Т) ба харакати чрхзании собитшитоб (ع = const) медарояд.
Дар втулка (гилофа)-и поёнии кафо (5) электромагнити тормодиихи махкам аст, ки хангоми ба он васл кардани шиддати электри бо ёрии муфта (пайвастгар)и фрикциони (таввасути моиш харакатовар ё аз харакат боздоранда) раккосак дар холати ороми нигох дошта ё рахо дода, имконияти ба харакат даровардани он фарохам оварда мешавад.
![]()
|
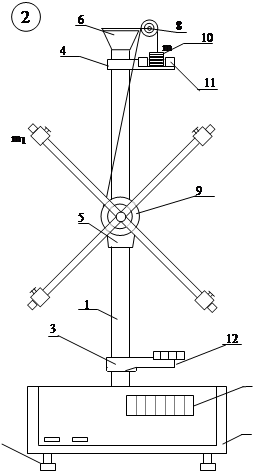 Кронштейни (дастак) харакатманди 4-ро ба рафти
сутунпояи 1 кучонда дар вазъияти ихтиёри махкам ва бо хамиг ин ё он баландии
борчахои 10-ро мукаррар сохтан мумкин аст. Барои ба хисоб гирифтани баландии
афтиши платформа (h) сутунпоя шкалаи таксимоташ
милиметри дорад. Дар кронштейни 4 ва кронштейни бехаракати 3 датчикро
(василахои ба кайдгири)-и фитоэлектри 11 ва 12 шинонда шудаанд. Датчики 11
хисобгираки вактро бо кор меандозаду датчики 12 импулси электрии анчоми кайди
вактро ангезонида, электромагнитро ба манбайи шиддати дойими васл менамояд ва
харакати раккосак катъ меёбад.
Кронштейни (дастак) харакатманди 4-ро ба рафти
сутунпояи 1 кучонда дар вазъияти ихтиёри махкам ва бо хамиг ин ё он баландии
борчахои 10-ро мукаррар сохтан мумкин аст. Барои ба хисоб гирифтани баландии
афтиши платформа (h) сутунпоя шкалаи таксимоташ
милиметри дорад. Дар кронштейни 4 ва кронштейни бехаракати 3 датчикро
(василахои ба кайдгири)-и фитоэлектри 11 ва 12 шинонда шудаанд. Датчики 11
хисобгираки вактро бо кор меандозаду датчики 12 импулси электрии анчоми кайди
вактро ангезонида, электромагнитро ба манбайи шиддати дойими васл менамояд ва
харакати раккосак катъ меёбад.
Дар асоси 2-и дастгох 7 шинонда шудаанд, ки бо ёрии онхо мавкейи шокули (вертикали)-и сутунпояро танзим додан имконпазир аст. Дар хамин асос барои чен ардани тули вакти афтиши платформаю борчахо миллисониясанчи 13 чойгир мебшад. Руяи пеши асос чузхои идоравии зеринро дарбар гирифтааст:
СЕТЬ – пахши ин клавиша (тугма) Баьди васли дастгох ба шабакаи шахри медарорад ва чарогакхои дадтчмкхои Фотоелектрирофурузон мегардонад .
СБРОС-пахши ин тугма ададхои индикатор (нишондиханда) –и миллисиониясанчро ба сифр (нуль) – х о Табдил медихад (агарто ин дам дар он ададхои дигар сабт ефта бошад).
ПУСК- тугмаи идораи электро-магнит, пахши он электро-магнитро рахо дода импулсе меангезад, ки ба андозагирии вакт ичозат мефармояду озод кардани тугма электромагнитро ба кор андохта, харакати раккосакро кат месозад.
Тамоми система, чи тавре ки зикр ёфт, бо тасироти кувваи тарангии расмон ба харакати чархзани медарояд ва моменти гардишовари он мувофики формулаи
M = T'ri (3)
![]()
![]()
![]() муайян карда мещавад, ки дар ин
ифода ri – радиуси диски ба он ресмон кашида
аст. Кувваи тарангии ресмонро ба татбики муодилаи (2) ба харакати пешравии
платформаю борчахои массаашон m (бо назардошти таъсири ду кувва –
кувваи тарангии ресмон T ва кувваи вазнинии P = mg ба ин ба ин систем) дар шакли проэкция ба рафти тири
координатии шокулан ба поён равонбурда дарёфтан мумкин аст:
муайян карда мещавад, ки дар ин
ифода ri – радиуси диски ба он ресмон кашида
аст. Кувваи тарангии ресмонро ба татбики муодилаи (2) ба харакати пешравии
платформаю борчахои массаашон m (бо назардошти таъсири ду кувва –
кувваи тарангии ресмон T ва кувваи вазнинии P = mg ба ин ба ин систем) дар шакли проэкция ба рафти тири
координатии шокулан ба поён равонбурда дарёфтан мумкин аст:
ma = mg – T
ё худ T = m (g – a) (4)
Дар ин ифода (٨ - шитоби хаттии харакати пешравии платформаю борчахо мебошад, ки онро тавассути кимати баландии ёфтиш h ва тули вакти харакат дар он t муайян мекунад:
a = 2h / t2 (5)
Шитоби кунчии харакати чархзании раккосак عбо шитоби а таносуби содда дорад:
ع = а / ri (6)
Пас, моменти кувваи тарангии ресмон (мувофики конуни сейуми Нютон Т = Т будунашро ба ътибор мегирем) бо формулаи
|
|
мукаррар карда мешавад. Аз ин ифода бамеояд, ки массаи борчахои 10 ва рудиуси дискро тагёир дода, моменти кувваи гардишоварро дигар кардан икон дорад.
овардан душвор нест, Махз хамин формула барои муайян кардан моменти инерцияи раккосак мавриди истифода карор меёбад.
Тачрибаи кор
1. Борхои m1 – ро, агар онхо дар милахр чойгир бошанд, чудо карда як су гузоред.
2. Бо ёрии штангенциркул радиусхои дискхо r1 ва r2 - ро чен карда дар чадвали 1 ба кайд гиред.
ЧАДВАЛИ № I
|
(ri), м |
(ri) |
m, кг |
Тули вакти афтиш |
<t> c |
<бt> c |
a, m/c |
ع род/с |
М, H.M |
Á кг.м2 |
бÁ, кг.м2 |
||||
|
t1 |
t2 |
t3 |
t4 |
t5 |
||||||||||
|
(ri) |
||||||||||||||
|
(ri) |
3. Дастгохро ба шабакаи шахри васлу тугмаи СЕТЬ – ро пахш намоедва санчед, ки чарогакхои датчикхои фотоэлктри фурузон бошад.
4. Як нуги расмонро ба диски радиусаш хурд (r/1) андармон карда, нуги дигари платформа овезонбударо аз гаргараи 8 гузаронед ва руяи поёнии платформаро мувофики нишонаи танаи датчики фотоэлектри болои (2) чойгир созед.
5. Тугмаи ПУСК-ро рахо (озод) ва тугмаи СБРОС-ро пахш карда санчед, ки дар индикатори миллисоничсанч ададхои якхелаи сифр (нуль) пайдо шаванд ва система аз харакат бозмонд. Аз руйи шкалаи сутунпоя ва нишонаи кронштейнт 4 баландии платформа h – ро муайян карда дар чадвали 1 ба кайд гиред/
6. Тугмаи ПУСК – ро карда, аз руйи индикатори миллисониясанч баъди аз харакат бозмондаи плаформа тули вантро ва кайд гиред. Тачрибаро камаш 5 маротиба барои хамон як массаи платформа борчахо, ки чи кадар буданашроустод тавсия медихад, такроран гузаронед ва натичахоро дар чадвали 1 гирд оваред.
7. Кимати миёнаи вакти афтиш:
 |
|||
|
|||
|
|
ва хатои хар як андозагирии ватро увофики фомулаи:
Δti = / ti - <t> /
|
![]()
|
муайян карда дар чадвали 1 ба кайд гиред.
8. Бо истифодаи формулахои (5) – (7) бузургихои а, ع ва М – ро хисоб карда, оменти инерцияи раккосаки холи Áo – ро мукаррар созед.
9. Нуги расмонро ба диски радиусаш калон (r2) андармон карда, пунктхои аз 4 то 8 – ро такроран ичро намоед ва натичахоро дар чадвали 1 гирд варед.
10. Хатои Миёнаи квадратии андозагирии моменти инерцияро мутобики формулаи (М. 18), ки дар сах. 13 оварда шудааст, ба хисоб гиред, хангоми хисобу китоб мувофики формулаи (7) ва бn = бr = 0,5 мм = 5. 10-4 м ( ба сах. 11 ниг.) буданашро дар назар доред. Бузургии бt - ро аз натичаи пункти 7 истифода баред.
Э З О Х: Киматхои ифодахи зайлро алохида хисоб ва онхоро мукоиса карда мукаррар созед, ки сахми кадоме аз онхо зийдтар аст. Дар мавриди хиссаи к а м т а р и н доштан ифода, онро сарфи назар кардан (партофтан) равост.
11.Ба миллахо борхои m1 – ро чуфт – чуфт дар фосилаи якхела (масалан, маротиби аввал онхоро ба дискхо чафо, маротиби дуйум дар миёнчой ва маротиби сайум дар нугхои милахо) махкам карда, барои хамон як массаи борчахои болои платформа пунктхои аз 4 то 8 – ро дар яке аз дискхо такроран гузаронед ва натичахоро дар чадвали 2 гирд оваред.
| № тачриба |
m1, кг |
m, кг | R, м |
Тули вакти афтиш |
<t> c |
a, m/c |
ع род/с |
М, H.M |
Áтач кг. м2 |
Áназ кг. м2 |
||||
|
t1 |
t2 |
t3 |
t4 |
t5 |
||||||||||
| 1 |
|
|||||||||||||
| 2 |
|
|||||||||||||
| 3 |
|
11. Мувофики формулаи (7) моменти инерцияи система Áтач – ро мукаррар созед ва онро бо кимати назарявии моменти инерцияи Áназ (дар холи борхои m1 – ро чун нуктахои модди пиндоштан ва хосияти аддитиви доштани моменти инерцияро ба назар гирифтан) тавассути формулаи
Áназ = Áо + km1 R2
( k – теъдоди борхои m1 ва он 2 ё 4 буда метавонад ) муйян намоед, ки дар ин ифода Áо – моменти инерцияи раккосаки холист ва кимати онро аз чадвали 1 аз хисоби миёнаи натичаи андозагири дар хар ду диск гирифтан мебояд. Хатои нисбии андоагириро дар ин маврид чун:
бÁ = (Áназ - Áтач) . 100%/Áназ
Машки иловаги. МУАЙЯН КАРДАНИ МОМЕНТИ КУВВАИ СОИШ
Дар холи ба тибор гирифтани куввахои соиш (Fc) муодилаи (1) намуди зайл мегирад:
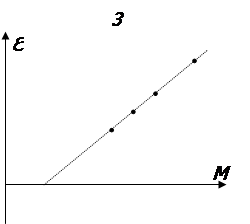
Áع = М - Мс,
ки дар он Мс – момонти уввахои соиш аст, Барои муайян кардани он аз графики вобастагии ع = f (M) истифода мебаранд. Бо ин максад а платформа бо навбат якчанд борчахои массааш маълум (аз чумла платформаи холи, ки массааш 0,053 кг) – ро чойгир карда, пунктхои аз 4 то 8-ро дар яке аз дискхо хар карат як борча гузошта такроран мегузаронанд ва мувофики формулахои (5) – (7) бузургихои а, ع ва М – ро чен карда, натичахоро дар чадвали 3 гирд оваред.
| № тачриба |
m1, кг |
m, кг | R, м |
Тули вакти афтиш |
<t> c |
a, m/c |
ع род/с |
М, H.M |
||||
|
t1 |
t2 |
t3 |
t4 |
t5 |
||||||||
| 1 |
|
|||||||||||
| 2 |
|
|||||||||||
| 3 |
|
|