Реферат: Элементарная теория радуги
Но что мной зримая вселена?
И что перед тобою я?
Ничто! Но ты во мне сияешь
Величеством твоих доброт.
Во мне себя преображаешь,
Как Солнце в малой капле вод.
Г. Р. Державин
Сколько бывает радуг?
Вряд ли найдется человек, который не любовался бы радугой. Появившись на небосводе, она невольно приковывает внимание. А сколько легенд и сказаний связано с радугой у разных народов! В русских летописях радуга называется « райской дугой » или сокращенно « райдугой ». В Древней Греции радугу олицетворяла богиня Ирида («Ирида» и означает « радуга »). По представлениям древних греков, радуга соединяет небо и землю, и Ирида была посредницей между богами и людьми. В русский язык вошли и другие слова с тем же греческим корнем: ирис — радужная оболочка глаза, иризация, иридий.
Радуга всегда связывается с Дождем. Она может появиться и перед дождем, и во время дождя, и после него, в зависимости от того, как перемещается облако, дающее ливневые осадки. Об этом говорят и народные поговорки: „Радуга-дуга! Перебей дождя!", „Радуга-дуга! Принеси нам дождь!"
Первая попытка объяснить радугу как естественное явление природы была сделана в 1611 г. архиепископом Антонио Доминисом. Его объяснение радуги противоречило библейскому, поэтому он был отлучен от церкви и приговорен к смертной казни. Антонио Доминис умер в тюрьме, не дождавшись казни, но его тело и рукописи были сожжены.
Обычно наблюдаемая радуга — это цветная дуга угловым радиусом 42°, видимая на фоне завесы ливневого дождя или полос падения дождя, часто не достигающих поверхности Земли. Радуга видна в стороне небосвода, противоположной Солнцу, и обязательно при Солнце, не закрытом облаками. Такие условия чаще всего создаются при выпадении летних ливневых дождей, называемых в народе « грибными » дождями. Центром радуги является точка, диаметрально противоположная Солнцу,— антисолярная точка. Внешняя дуга радуги красная, за нею идет оранжевая, желтая, зеленая дуги и т. д., кончая внутренней фиолетовой.
Сколько радуг можно увидеть одновременно?
Неискушенный наблюдатель видит обычно одну радугу, изредка две. Причем вторая радуга, концентрическая с первой, имеет угловой радиус около 50° и располагается над первой. Вторая радуга более широкая, блеклая, расположение цветов в ней обратное первой радуге: внешняя дуга у нее фиолетовая, а внутренняя красная.
Самое удивительное, что большинство людей, наблюдавших радугу много раз, не видят, а точнее не замечают дополнительных дуг в виде нежнейших цветных арок внутри первой и снаружи второй радуг (т. е. со стороны фиолетовых краев радуг). Эти цветные дуги (их обычно три-четыре) неправильно названы дополнительными — в действительности они такие же основные (или главные), как первая и вторая радуги.
Эти дуги не образуют целого полукруга или большой дуги и видны только в самых верхних частях радуг, т. е. вблизи « вершин », или « макушек », основных радуг, когда же последние переходят в вертикальное положение (или близкое к нему), дополнительные дуги пропадают. Именно в этих дугах, а не в основных, сосредоточено наибольшее богатство чистых цветовых тонов, которое и породило выражение „все цвета радуги".
Радуги можно увидеть около водопадов, фонтанов, на фоне завесы капель, разбрызгиваемых поливальной машиной или полевой поливальной установкой. Можно самому создать завесу капель из ручного пульверизатора и, встав спиною к Солнцу, увидеть радугу, созданную собственными руками. У фонтанов и водопадов случалось видеть, кроме описанных двух основных и трех-четырех дополнительных дуг к каждой основной, еще одну или две радуги вокруг Солнца.
Как возникает радуга?
Откуда берется удивительный красочный свет, исходящий от дуг радуги? Все радуги — это солнечный свет, разложенный на компоненты и перемещенный по небосводу таким образом, что он кажется исходящим от части небосвода, противоположной той, где находится Солнце.
Научное объяснение радуги впервые дал Репе Декарт в 1637 г. Декарт объяснил радугу на основании законов преломления и отражения солнечного света в каплях выпадающего дождя. В то время еще не была открыта дисперсия — разложение белого света в спектр при преломлении. Поэтому радуга Декарта была белой.
Спустя 30 лет Исаак Ньютон, открывший дисперсию белого света при преломлении, дополнил теорию Декарта, объяснив, как преломляются цветные лучи в каплях дождя. По образному выражению американского ученого А. Фразера, сделавшего ряд интересных исследований радуги уже в наше время, „Декарт повесил радугу в нужном месте на небосводе, а Ньютон расцветил ее всеми красками спектра".
Несмотря на то что теория радуги Декарта — Ньютона создана более 300 лет назад, она правильно объясняет основные особенности радуги: положение главных дуг, их угловые размеры, расположение цветов в радугах различных порядков.
Для объяснения радуги мы пока и ограничимся теорией Декарта — Ньютона, которая подкупает своей удивительной наглядностью и простотой.
Лучи радуги
Итак, пусть параллельный пучок солнечных лучей падает на каплю (рис. 1). Ввиду того что поверхность капли кривая, у разных лучей будут разные углы падения. Они изменяются от 0 до 90°. Проследим путь луча, упавшего в точку А, его угол паления обозначим i . Преломившись под углом преломления r , луч входит в каплю и доходит до точки В. Часть энергии луча, преломившись, выходит из капли, часть, испытав внутреннее отражение в точке 5, идет внутри капли до точки С. Здесь снова часть энергии луча, преломившись, выходит из капли, а некоторая часть, испытав второе внутреннее отражение, доходит до точки О и т. д. В .принципе луч может испытывать любое число (и), внутренних отражений, а преломлений у каждого луча два — при входе и при выходе из капли.
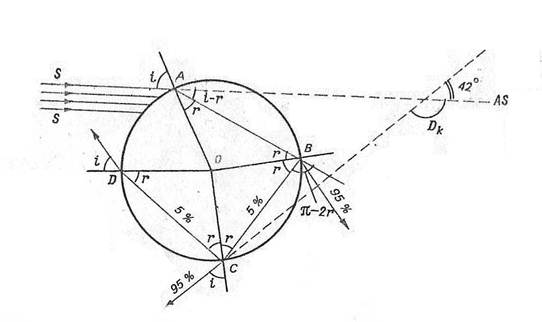
Рис. 1. Ход светового луча в капле при образовании первой и второй радуг.
Обозначим Dk угол отклонения любого луча после прохождения им капли. Тогда из рис.1 очевидно, что
Dk = 2( i - r) + k (p – 2r), (1)
здесь k — число внутренних отражений луча.
Параллельный пучок лучей, падающий на каплю, по выходе из капли оказывается сильно расходящимся (рис. 2). Концентрация лучей, а значит, и их интенсивность тем больше, чем ближе они лежат к лучу, испытавшему минимальное отклонение. Путь минимально отклоненного луча обозначен на рисунке пунктиром. Только минимально отклоненный луч и самые близкие к нему лучи обладают достаточной интенсивностью, чтобы образовать радугу. Поэтому этот луч и называют лучом радуги.
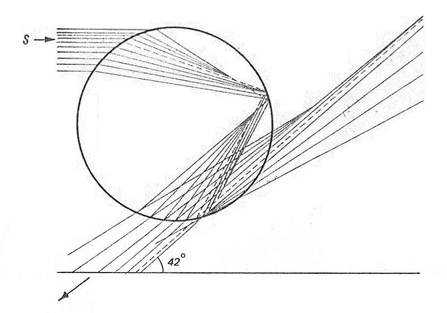
Рис.2. Преломление пучка световых лучей в капле.
Минимальное отклонение луча, испытавшего одно внутреннее отражение (k = 1), по теории Декарта равно:
D1 = p +2( i – 2r). (2)
Каждый белый луч, преломляясь в капле, разлагается в спектр, и из капли выходит пучок расходящихся цветных лучей. Поскольку у красных лучей показатель преломления меньше, чем у других цветных лучей, то они и будут испытывать минимальное отклонение по сравнению с остальными. Минимальные отклонения крайних цветных лучей видимого спектра красных и фиолетовых оказываются следующими: D1k= 137°30' и D1ф = 139°20'. Остальные цветные лучи займут промежуточные между ними положения.
Солнечные лучи, прошедшие через каплю с одним, внутренним отражением, оказываются исходящими от точек неба, расположенных ближе к антисолярной точке, чем к Солнцу. Поэтому, чтобы увидеть эти лучи, надо встать спиной к Солнцу. Расстояния их от антисолярной точки будут равны соответственно: 180° — 137°30' = 42°30' для красных и 180° — 139°20' = 40°40' для фиолетовых.
Почему радуга круглая? Дело в том, что более или менее сферическая капля, освещенная параллельным пучком лучей солнечного света, может образовать радугу только в виде круга. Поясним это.
Описанный путь в капле с минимальным отклонением по выходе из нее проделывает не только тот луч, за которым мы следили, но также и многие другие лучи, упавшие на каплю под таким же углом. Все эти лучи и образуют радугу, поэтому их называют лучами радуги.
Сколько же лучей радуги в пучке света, падающего на каплю? Их много, по существу, они образуют целый цилиндр. Геометрическое место точек их падения на каплю это целая окружность.
В результате прохождения через каплю и преломления в ней цилиндр белых лучей преобразуется в серию цветных воронок, вставленных одна в другую, с центром в антисолярной точке, с открытыми раструбами, обращенными к наблюдателю. Наружная воронка красная, в нее вставлена оранжевая, желтая, далее идет зеленая и т. д., кончая внутренней фиолетовой.
Таким образом, каждая отдельная капля образует целую радугу! Радуга - „как Солнце в малой капле вод". Так образно и предельно лаконично выразил суть радуги Г. Р. Державин.
Конечно, радуга от одной капли слабая, и в природе ее невозможно увидеть отдельно, так как капель в завесе дождя много. В лаборатории же удавалось наблюдать не одну, а несколько радуг, образованных преломлением света в одной подвешенной капельке воды или масла при освещении ее лучом лазера. Подробнее об этом эксперименте рассказано ниже.
Радуга, которую мы видим на небосводе, мозаична — она образована мириадами капель. Каждая капля создает серию вложенных одна о другую цветных воронок (или конусов). Но от отдельной капли в радугу попадает только один цветной луч. Глаз наблюдателя является общей точкой, в которой пересекаются цветные лучи от множества капель. Например, все красные лучи, вышедшие из различных капель, но под одним и тем же углом и попавшие в глаз наблюдателю, образуют красную дугу радуги, также и все оранжевые и другие цветные лучи. Поэтому радуга круглая.
Два человека, стоящие рядом, видят каждый свою радугу. Если вы идете по дороге и смотрите на радугу, она перемещается вместе с вами, будучи в каждый момент образована преломлением солнечных лучей в новых и новых каплях. Далее, капли дождя падают. Место упавшей капли занимает другая и успевает послать свои цветные лучи в радугу, за ней следующая и т. д. Пока идет дождь, мы видим радугу.
Мы пояснили, как образуется первая радуга, наиболее часто наблюдаемая, с ярким внешним красным краем и внутренним фиолетовым.
Найдем ширину первой радуги D1, т. е. угловое расстояние от ее красной дуги до фиолетовой с учетом поправки на угловую ширину Солнца, диаметр которого равен 32': D1= 42°30' - 40°40' +32' = 2°22'.
Вторая радуга и следующие
Если повторить предыдущие рассуждения относительно лучей, испытавших в капле два внутренних отражения, получим следующие минимальные углы отклонения крайних цветных лучей. Для красных D2k= 230°54' и для фиолетовых D2ф = 233°56'. Такие лучи так же, как и испытавшие одно отражение внутри капли, лежат ближе к антисолярной точке, чем к Солнцу. Угловые расстояния их от антисолярной точки будут равны: 230°54' — 180° = 50°34' для красных; 233°46' — 180° = 53°56' для фиолетовых. Эти лучи образуют радугу, концентрическую с первой, но с обратным расположением цветов. В этой радуге внутренняя дуга красная.
Угловая ширина второй радуги D2 = 53°56' — 50"34' = 3°54'.
Вторая радуга значительно шире первой и выглядит более слабой.
Расчеты для радуг следующих порядков ( k = 3, 4, 5, 6, 7, 8 и т. д.) показали, что 3-я и 4-я радуги располагаются вокруг Солнца, 5-я и 6-я — вокруг антисолярной точки, 7-я и 8-я — снова вокруг Солнца и т. д.
В таблице приведены углы отклонения лучей красного цвета, угловые радиусы соответствующих радуг и положение их на небосводе согласно расчетам К. С. Шифрина по формулам дифракции.
| k |
Dk |
Угловой радиус радуги | Положение на небосводе |
| 1 | 137°29¢ | 42°31¢ | Вокруг антисолярной точки |
| 2 | 129°54¢ | 50°06¢ | |
| 3 | 42°53¢ | 42°53¢ | Вокруг Солнца |
| 4 | 42°18¢ | 42°18¢ | |
| 5 | 126°31¢ | 53°29¢ | Вокруг антисолярной точки |
| 6 | 149°46¢ | 30°14¢ | |
| 7 | 66°22¢ | 66°22¢ | Вокруг Солнца |
| 8 | 16°51¢ | 16°51¢ |
Возникает вопрос: почему мы не видим всех радуг? Это происходит потому, что из всей энергии луча, упавшего на каплю в точку А, примерно 7% отражается, 88% - проходит сквозь каплю и только 5% испытывает одно внутреннее отражение в точке В и идет дальше к точке С. Здесь снова происходит аналогичное разделение энергии между лучами, выходящими из капли и дважды отраженными от внутренней поверхности капли. Поэтому на радуги всех порядков расходуется менее 5% энергии падающего пучка, при этом „львиная" доля — около 4% — идет на образование первой радуги. Обычно мы и можем видеть только первую радугу и изредка вторую. На остальные радуги остается слишком мало энергии, менее 1%, поэтому радуги высоких порядков не видны.
Почему радуга бывает разной?
По теории Декарта — Ньютона радуга должна быть всегда одинаковой — „застывшей". Эти ученые правильно объяснили положение радуги на небосводе, размер дуг, расположение цветов в основных радугах любого порядка. В частности, по теории ширине дуг радуг всегда было „положено" быть одной и той же. Однако радуга содержала еще много секретов. Внимательный наблюдатель видел иногда серию красочных дополнительных дуг, которым совсем „не было места" в теории Декарта — Ньютона. Иногда радуга имела яркие насыщенные тона, а порой была совсем блеклой, почти белой. Радуга бывала и широкой и узкой — и всё это „не укладывалось" в теорию Декарта — Ньютона.
Объяснение всего комплекса радуги, со всеми неразгаданными, ее особенностями, было сделано позже, когда была создана общая теория рассеяния (дифракции) световых лучей в атмосфере. В частности, стало ясно, что дополнительные дуги возникают вследствие интерференции лучей, лежавших но обе стороны от наименее отклоненного луча (луча радуги) и в непосредственной близости от него.
Размер и форма капель и их влияние на вид радуги
Расчеты по формулам дифракционной теории, выполненные для капель разного размера, показали, что весь вид радуги — ширина дуг, наличие, расположение и яркость отдельных цветовых тонов, положение дополнительных дуг очень сильно зависят от размера капель дождя. Приведем основные характеристики внешнего вида радуги для капель разных радиусов.
Радиус капель 0,5—1 мм. Наружный край основной радуги яркий, темно-красный, за ним идет светло-красный и далее чередуются все цвета радуги. Особенно яркими кажутся фиолетовый и зеленый. Дополнительных дуг много (до пяти), в них чередуются фиолетово-розовые тона с зелеными. Дополнительные дуги непосредственно примыкают к основным радугам.
Радиус капель 0,25 мм. Красный кран радуги стал слабее. Остальные цвета видны по-прежнему. Несколько фиолетово-розовых дополнительных дуг сменяются зелеными.
Радиус капель 0,10—0,15 мм. Красного цвета в основной радуге больше нет. Наружный край радуги оранжевый. В остальном радуга хорошо развита. Дополнительные дуги становятся все более желтыми. Между ними и между основной радугой и первой дополнительной появились просветы.
Радиус капель 0,04—0,05 мм. Радуга стала заметно шире и бледнее, Наружный край ее бледно-желтый. Самым ярким является фиолетовый цвет. Первая дополнительная дуга отделена от основной радуги довольно широким промежутком, цвет ее белесый, чуть зеленоватый и беловато-фиолетовый.
Радиус капель 0,03 мм. Основная радуга еще более широкая с очень слабо окрашенным чуть желтоватым краем, содержит отдельные белые полосы.
Радиус капель 0,025 мм и менее. Радуга стала совсем белой. Она примерно в два раза шире обычной радуги и имеет вид блестящей белой полосы. Внутри нее могут быть дополнительные окрашенные дуги, сначала бледно-голубые или зеленые, затем белесовато-красные.
Таким образом, по виду радуги можно приближенно оценить размеры капель дождя, образовавших эту радугу. В целом, чем крупнее капли дождя, тем радуга получается уже и ярче, особенно характерным для крупных капель является наличие насыщенного красного цвета в основной радуге. Многочисленные дополнительные дуги также имеют яркие тона и непосредственно, без промежутков, примыкают к основным радугам. Чем капли мельче, тем радуга становится более широкой и блеклой с оранжевым или желтым краем. Дополнительные дуги дальше отстоят и друг от друга и от основных радуг.
Вид радуги зависит и от формы капель. При падении в воздухе крупные капли сплющиваются, теряют свою сферичность. Вертикальное сечение таких капель приближается к элипсу. Расчеты показали, что минимальное отклонение красных лучей при прохождении через сплющенные капли радиусом 0,5 мм составляет 140°. Поэтому угловой размер красной дуги будет не 42°, а только 40°. Для более крупных капель, например радиусом 1,0 мм, минимальное отклонение красных лучей составит 149°, а красная дуга радуги будет иметь размер 31°, вместо 42°. Таким образом, чем сильнее сплющивание капель, тем меньше радиус образуемой ими радуги.
Разгадан „секрет" добавочных дуг!
А. Фразер, рассмотрев одновременно влияние размера и формы капель на вид радуги, сумел раскрыть «секрет» возникновения добавочных дуг. Как только что было сказано, уменьшение размера преобладающих капель и сплющивание крупных действуют в противоположных направлениях. Что же пересилит? Когда и какое влияние будет преобладающим?
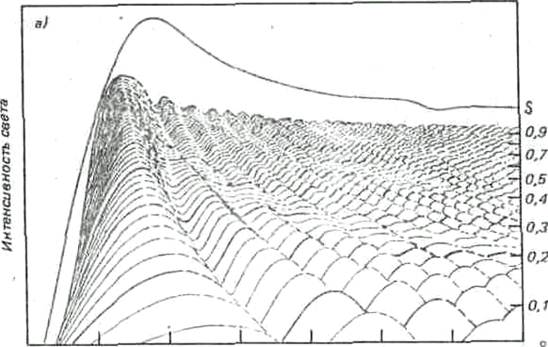
Наглядной иллюстрацией взаимодействия обоих факторов и совместного их влияния на вид радуги являются рис. 3 а и б, составленные А. Фразером, на основании расчетов: На этих рисунках показано распределение интенсивности света в основной радуге и дополнительных дугах в зависимости от размера капель.
Сложная волнообразная поверхность на переднем плане (рис.3 а) составлена из многих индивидуальных кривых. Каждая кривая дает распределение и интенсивность света в радуге от одной капли. Каждая пятая кривая проведена потолще, цифры справа означают радиус капли, соответствующей кривой, в миллиметрах. Все кривые начинаются слева с очень малой интенсивности (вне радуг), затем быстро поднимаются до максимума между 138° и 139° (первая радуга). Следующий гребень справа — первая дополнительная дуга, за ней вторая дополнительная дуга и т. д. Расстояние между дугами, как видно из рисунка, быстро уменьшается при увеличении радиуса капель. Это действие первого фактора. Радуга становится узкой при увеличении размера капель.
Верхняя кривая S — это результирующая сложения вкладов капель всех размеров. Она характеризует распределение интенсивности света в окончательной радуге, которую мы видим.
137 138 139 140 141 142 143 144
Угловое расстояние от Солнца
137 138 139 140 141 142 143 144
Угловое расстояние от Солнца
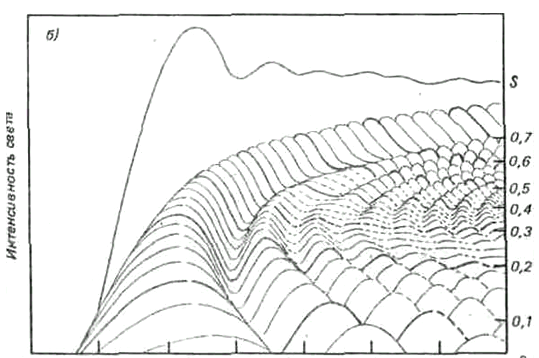
Рис. 3. Распределение интенсивности света в основной радуге и дополнительных дугах в зависимости от размера капель.
а — без учёта сплющивания капель; б — с учетом сплющивания капель. S — суммарная кривая.
На рис.3 б показаны те же кривые, но теперь учтено влияние сплющивания капель, тем более сильное, чем крупнее капли. Индивидуальные кривые для крупных сплющенных капель смещены в сторону больших минимальных углов отклонения от Солнца (или, что то же, в сторону уменьшения радиусов радуг), и в результате вся волнообразная поверхность оказалась изогнутой вправо (индивидуальные максимумы ушли вправо). Это привело к тому, что на результирующей суммарной кривой появились, помимо основной радуги, еще дополнительные дуги, на угловых расстояниях от Солнца: первая —140,5°, вторая —141,3°, третья — 142,4°, четвертая—142,5°.
Дополнительные дуги видны только вблизи вершины основной радуги, так как они образованы только вертикальными или близкими к ним лучами, прошедшими через эллиптические сечения капель.
Расчетами показано, но это можно проследить и по рис.3 б, что дополнительные, дуги создаются в основном каплями размером от 0,2 до 0,3 мм. Более крупные и более мелкие капли дают максимумы, накладывающиеся друг на друга и слишком далеко отстоящие от основной радуги (они уходят вправо). Радуги капель диаметром 0,2—0,3 мм находятся в преимущественном положении, поскольку их максимумы никуда не сместились. Таким образом, можно сделать вывод, что дополнительные дуги видны, если в ливневом дожде присутствуют в значительном, количестве капли радиусом 0,25 мм и мало более крупных капель, смазывающих картину. Поэтому дополнительные дуги чаще видны и наиболее красочны не в очень интенсивных летних ливневых дождях. Они появляются также на фоне завесы из мельчайших капель, образующихся при разбрызгивании воды в поливальных установках.
Можно ли видеть целый круг радуги? С поверхности Земли мы можем наблюдать радугу в лучшем случае в виде половины круга, когда Солнце находится на горизонте. При поднятии Солнца радуга уходит под горизонт. Первую радугу можно, видеть при высотах Солнца более 42°, а вторую — более 50°. С самолета, а еще лучше с вертолета (больше обзор) можно наблюдать радугу в виде целого круга! Описание такой круговой радуги (ее и радугой, т. е. дугой, уже неудобно называть!) было помещено в журнале „Природа". Ее видели пассажиры самолета, летевшего в районе Новосибирска на высоте 1000 м.
Поляризация света радуг. Свет радуги характеризуется необычийно высокой степенью поляризации. В первой радуге она достигает 90%, во второй—около 80%. В этом легко убедиться, если посмотреть на радугу через поляризационную призму Николя. При небольших углах поворота призмы радуга полностью пропадает.
Радуга без дождя?
Бывают ли радуги без дождя или без полос падения дождя? Оказывается, бывают — в лаборатории. Искусственные радуги создавались в результате преломления света в одной подвешенной капельке дистиллированной воды, воды с сиропом или прозрачного масла. Размеры капель варьировали от 1,5 до 4,5 мм. Тяжелые капли вытягивались под действием силы тяжести, и их сечение в вертикальной плоскости представляло собою эллипс. При освещении капельки лучом гелий-неонового лазера (с длиной волны 0,6328 мкм) появлялись не только первая и вторая радуги, но и необычайно яркие третья и четвертая, с центром вокруг источника света (в данном случае лазера). Иногда удавалось получать даже пятую и шестую радуги. Эти радуги, как первая и вторая, снопа были в стороне, противоположной источнику.
Итак, одна капелька создала столько радуг! Правда, эти радуги не были радужными. Все они были одноцветными, красными, так как образованы не белым источником света, а монохроматическим красным лучом.
Туманная радуга
В природе встречаются белые радуги, о которых говорилось выше. Они появляются при освещении солнечными лучами слабого тумана, состоящего из капелек радиусом 0,025 мм или менее. Их называют туманными радугами. Кроме основной радуги в виде блестящей белой дуги с едва заметным желтоватым краем наблюдаются иногда окрашенные дополнительные дуги: очень слабая голубая или зеленая дуга, а затем белесовато-красная.
Аналогичного вида белую радугу можно увидеть, когда луч прожектора, расположенного сзади вас, освещает интенсивную дымку или слабый туман перед вами. Даже уличный фонарь может создать, хотя и очень слабую, белую радугу, видимую на темном фоне ночного неба.
Лунные радуги
Аналогично солнечным могут возникнуть и лунные радуги. Они более слабые и появляются при полной Луне. Лунные радуги явление более редкое, чем солнечные. Для их возникновения необходимо сочетание двух условий: полная Луна, не закрытая облаками, и выпадение ливневого дождя или полос его падения (не достигающих Земли). Ливневые дожди, обусловленные дневными конвективными движениями воздуха, значительно реже выпадают ночью.
Лунные радуги могут наблюдаться в любом месте земного шара, где осуществятся перечисленные два условия.
Дневные, солнечные радуги, даже образованные самими мелкими каплями дождя или тумана, довольно белесые, светлые, и все же наружный край их хотя бы слабо, но окрашен в оранжевый или желтый цвет. Радуги, образованные лунными лучами, совсем не оправдывают своего названия, так как они не радужные и выглядят как светлые, совершенно белые дуги.
Отсутствие красного цвета у лунных радуг даже при крупных каплях ливневого дождя объясняется низким уровнем освещения ночью, при котором полностью теряется чувствительность глаза к лучам красного цвета. Остальные цветные лучи радуги также теряют в значительной степени свой цветовой тон из-за ахроматичности (неокрашенности) ночного зрения человека.
Министерство общего и профессионального образования Российской Федерации
Дальневосточный Государственный Технический Университет
Кафедра физики
Реферат
Тема: Элементарная теория радуги.
Выполнил:
Проверил: Гайдай Л.И.
Владивосток 2001г.
Список литературы
1. Суорд, Клиффорд «Необыкновенная физика обыкновенных явлений»
2. Тарасов Л.В. «Физика в природе», М.- 1989.
3. Зверева В.Л. «Солнечный свет в атмосфере», М.-1988.