Реферат: Анализ экономических задач симплексным методом
Введение.
Многие задачи, с которыми приходится иметь дело в повседневной практике, являются многовариантными. Среди множества возможных вариантов в условиях рыночных отношений приходится отыскивать наилучшие в некотором смысле при ограничениях, налагаемых на природные, экономические и технологические возможности. В связи с этим возникла необходимость применять для анализа и синтеза экономических ситуаций и систем математические методы и современную вычислительную технику? Такие методы объединяются под общим названием — математическое программирование.
Математическое программирование — область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.
Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием оптимальности. Экономические возможности формализуются в виде системы ограничений. Все это составляет математическую модель. Математическая модель задачи — это отражение оригинала в виде функций, уравнений, неравенств, цифр и т. д. Модель задачи математического программирования включает:
1) совокупность неизвестных величин, действуя на которые, систему можно совершенствовать. Их называют планом задачи (вектором управления, решением, управлением, стратегией, поведением и др.);
2) целевую функцию (функцию цели, показатель эффективности, критерий оптимальности, функционал задачи и др.). Целевая функция позволяет выбирать наилучший вариант -из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение. Это может быть прибыль, объем выпуска или реализации, затраты производства, издержки обращения, уровень обслуживания или дефицитности, число комплектов, отходы и т. д.;
Эти условия следуют из ограниченности ресурсов, которыми располагает общество в любой момент времени, из необходимости удовлетворения насущных потребностей, из условий производственных и технологических процессов. Ограниченными являются не только материальные, финансовые и трудовые ресурсы. Таковыми могут быть возможности технического, технологического и вообще научного потенциала. Нередко потребности превышают возможности их удовлетворения. Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений (область экономических возможностей). План, удовлетворяющий системе ограничений задачи, называется допустимым. Допустимый план, доставляющий функции цели экстремальное значение, называется оптимальным. Оптимальное решение, вообще говоря, не обязательно единственно, возможны случаи, когда оно не существует, имеется конечное или бесчисленное множество оптимальных решений.
Один из разделов математического программирования - линейным программированием. Методы и модели линейного программирования широко применяются при оптимизации процессов во всех отраслях народного хозяйства: при разработке производственной программы предприятия, распределении ее по исполнителям, при размещении заказов между исполнителями и по временным интервалам, при определении наилучшего ассортимента выпускаемой продукции, в задачах перспективного, текущего и оперативного планирования и управления; при планировании грузопотоков, определении плана товарооборота и его распределении; в задачах развития и размещения производительных сил, баз и складов систем обращения материальных ресурсов и т. д. Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление смесей, раскрой материалов), производственно-транспортных и других задач.
Начало линейному программированию было положено в 1939 г. советским математиком-экономистом Л. В. Канторовичем в работе «Математические методы организации и планирования производства». Появление этой работы открыло новый этап в применении математики в экономике. Спустя десять лет американский математик Дж. Данциг разработал эффективный метод решения данного класса задач — симплекс-метод. Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит в следующем:
1) умение находить начальный опорный план;
2) наличие признака оптимальности опорного плана;
3) умение переходить к нехудшему опорному плану.
§1.Задача линейного программирования и ![]() свойства
свойства![]() ее решений.
ее решений.
1.1 Понятие линейного программирования. Линейное программирование—раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.
Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов.
Формы записи задачи линейного программирования:
Общей задачей линейного программирования называют задачу
![]() (1)
(1)
при ограничениях
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() - произвольные
- произвольные ![]() (6)
(6)
где ![]() - заданные действительные
числа; (1) – целевая функция; (1) – (6) –ограничения;
- заданные действительные
числа; (1) – целевая функция; (1) – (6) –ограничения;
![]() - план задачи.
- план задачи.
1.2 Свойства решений.
Пусть ЗПЛ представлена в следующей записи:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Чтобы задача (7) – (8)
имела решение, системе её ограничений (8) должна быть совместной. Это возможно,
если r этой системы не больше числа
неизвестных n. Случай r>n вообще невозможен. При r= n система имеет единственное решение, которое будет при
![]() оптимальным. В этом случае
проблема выбора оптимального решения теряет смысл. Выясним структуру координат
угловой точки многогранных решений. Пусть r<n. В этом случае система векторов
оптимальным. В этом случае
проблема выбора оптимального решения теряет смысл. Выясним структуру координат
угловой точки многогранных решений. Пусть r<n. В этом случае система векторов ![]() содержит базис —
максимальную линейно независимую подсистему векторов, через которую любой
вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще
говоря, может быть несколько, но не более
содержит базис —
максимальную линейно независимую подсистему векторов, через которую любой
вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще
говоря, может быть несколько, но не более ![]() .
Каждый из них состоит точно из r
векторов. Переменные ЗЛП, соответствующие r векторам базиса, называют, как известно, базисными и
обозначают БП. Остальные n – r переменных
будут свободными, их обозначают СП. Не
ограничивая общности, будем считать, что базис составляют первые m векторов
.
Каждый из них состоит точно из r
векторов. Переменные ЗЛП, соответствующие r векторам базиса, называют, как известно, базисными и
обозначают БП. Остальные n – r переменных
будут свободными, их обозначают СП. Не
ограничивая общности, будем считать, что базис составляют первые m векторов ![]() .
Этому базису соответствуют базисные переменные
.
Этому базису соответствуют базисные переменные ![]() ,
а свободными будут переменные
,
а свободными будут переменные ![]() .
.
Если свободные переменные приравнять нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (8) называют опорным решением (планом).
Теорема. Если система векторов ![]() содержит m линейно независимых векторов
содержит m линейно независимых векторов ![]() , то допустимый план
, то допустимый план ![]() (10) является крайней точкой многогранника
планов.
(10) является крайней точкой многогранника
планов.
Теорема. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.
§2.Графический способ решения ЗЛП.
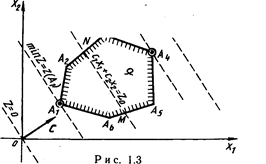
Геометрическая интерпретация экономических задач дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства ОЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации.
Пусть дана задача
![]() (11)
(11)
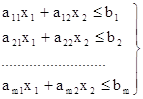 (12)
(12)
![]() (13)
(13)
Дадим геометрическую
интерпретацию элементов этой задачи. Каждое из ограничений (12), (13) задает на
плоскости ![]() некоторую полуплоскость. Полуплоскость
— выпуклое множество. Но пересечение любого числа выпуклых множеств является
выпуклым множеством. Отсюда следует, что область допустимых решений задачи
(11) — (13) есть выпуклое множество.
некоторую полуплоскость. Полуплоскость
— выпуклое множество. Но пересечение любого числа выпуклых множеств является
выпуклым множеством. Отсюда следует, что область допустимых решений задачи
(11) — (13) есть выпуклое множество.
Перейдем к геометрической
интерпретации целевой функции. Пусть область допустимых решений ЗЛП — непустое
множество, например многоугольник ![]() .
.
Выберем произвольное
значение целевой функции ![]() .
Получим
.
Получим ![]() . Это уравнение прямой
линии. В точках прямой NМ целевая функция сохраняет одно и то же
постоянное значение
. Это уравнение прямой
линии. В точках прямой NМ целевая функция сохраняет одно и то же
постоянное значение ![]() . Считая в равенстве
(11)
. Считая в равенстве
(11) ![]() параметром, получим
уравнение семейства параллельных прямых, называемых линиями уровня целевой
функции (линиями постоянного значения).
параметром, получим
уравнение семейства параллельных прямых, называемых линиями уровня целевой
функции (линиями постоянного значения).
Найдём частные
производные целевой функции по ![]() и
и ![]()
![]() (14)
(14)
![]() (15)
(15)
Частная производная (14)
((15)) функции показывает скорость ее возрастания вдоль данной оси. Следовательно,
![]() и
и ![]() — скорости
возрастания
— скорости
возрастания ![]() соответственно вдоль осей
соответственно вдоль осей ![]() и
и ![]() . Вектор
. Вектор ![]() называется градиентом
функции. Он показывает направление наискорейшего возрастания целевой функции:
называется градиентом
функции. Он показывает направление наискорейшего возрастания целевой функции:
![]()
Вектор —![]() указывает направление
наискорейшего убывания целевой функции. Его называют антиградиентом.
указывает направление
наискорейшего убывания целевой функции. Его называют антиградиентом.
Вектор ![]() перпендикулярен к прямым
перпендикулярен к прямым ![]() семейства
семейства ![]()
Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок ее графического решения.
1.
С учетом системы
ограничений строим область допустимых решений ![]()
2.
Строим вектор ![]() наискорейшего возрастания
целевой функции — вектор градиентного направления.
наискорейшего возрастания
целевой функции — вектор градиентного направления.
3.
Проводим
произвольную линию уровня ![]()
4.
При решении
задачи на максимум перемещаем линию уровня ![]() в
направлении вектора
в
направлении вектора ![]() так, чтобы она
касалась области допустимых решений в ее крайнем положении (крайней точке).
В случае решения задачи на минимум линию уровня
так, чтобы она
касалась области допустимых решений в ее крайнем положении (крайней точке).
В случае решения задачи на минимум линию уровня ![]() перемещают в
антиградиентном направлении
перемещают в
антиградиентном направлении
5.
Определяем
оптимальный план ![]() и экстремальное
значение целевой функции
и экстремальное
значение целевой функции ![]() .
.
§3.Симплексный метод.
Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит
1) умение находить начальный опорный план;
2) наличие признака оптимальности опорного плана;
3) умение переходить к нехудшему опорному плану.
Пусть ЗЛП представлена системой ограничений в каноническом виде:
![]() .
.
Говорят, что ограничение ЗЛП имеет
предпочтительный вид, если при неотрицательной правой части ![]() левая часть ограничений
содержит переменную, входящую с коэффициентом, равным единице, а в остальные
ограничения равенства - с коэффициентом, равным нулю.
левая часть ограничений
содержит переменную, входящую с коэффициентом, равным единице, а в остальные
ограничения равенства - с коэффициентом, равным нулю.
Пусть система ограничений имеет вид
![]()
Сведем задачу к каноническому виду.
Для этого прибавим к левым частям неравенств дополнительные переменные ![]()
![]() . Получим систему, эквивалентную
исходной:
. Получим систему, эквивалентную
исходной:
![]() ,
,
которая имеет предпочтительный вид
![]() .
.
В целевую функцию дополнительные
переменные вводятся с коэффициентами, равными нулю ![]()
![]() .
.
Пусть далее система ограничений имеет вид
![]()
Сведём её к эквивалентной вычитанием
дополнительных переменных ![]()
![]() из левых частей неравенств
системы. Получим систему
из левых частей неравенств
системы. Получим систему
![]()
Однако теперь система ограничений не
имеет предпочтительного вида, так как дополнительные переменные ![]() входят в левую часть (при
входят в левую часть (при ![]() ) с коэффициентами, равными
–1. Поэтому, вообще говоря, базисный план
) с коэффициентами, равными
–1. Поэтому, вообще говоря, базисный план ![]() не
является допустимым. В этом случае вводится так называемый искусственный базис.
К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют
искусственные переменные
не
является допустимым. В этом случае вводится так называемый искусственный базис.
К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют
искусственные переменные ![]() . В
целевую функцию переменные
. В
целевую функцию переменные ![]() , вводят
с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для
задачи на максимум, где М - большое положительное число. Полученная задача
называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный
вид.
, вводят
с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для
задачи на максимум, где М - большое положительное число. Полученная задача
называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный
вид.
Пусть исходная ЗЛП имеет вид
![]() (1)
(1)
![]() (2)
(2)
![]()
![]() (3)
(3)
причём ни одно из ограничений не имеет предпочтительной переменной. М-задача запишется так:
![]() (4)
(4)
![]() (5)
(5)
![]()
![]() ,
,
![]() ,
, ![]() (6)
(6)
Задача (4)-(6) имеет предпочтительный план. Её начальный опорный план имеет вид
![]()
Если некоторые из уравнений (2) имеют предпочтительный вид, то в них не следует вводить искусственные переменные.
Теорема. Если в оптимальном плане
![]() (7)
(7)
М-задачи (4)-(6) все искусственные
переменные ![]()
![]() , то план
, то план ![]() является оптимальным планом
исходной задачи (1)-(3).
является оптимальным планом
исходной задачи (1)-(3).
Для того чтобы решить задачу с
ограничениями, не имеющими предпочтительного вида, вводят искусственный базис и
решают расширенную М-задачу, которая имеет начальный опорный план ![]()
Решение исходной задачи симплексным
методом путем введения искусственных переменных ![]() называется
симплексным методом с искусственным базисом.
называется
симплексным методом с искусственным базисом.
Если в результате применения
симплексного метода к расширенной задаче получен оптимальный план, в котором
все искусственные переменные ![]() , то его
первые n компоненты дают оптимальный план
исходной задачи.
, то его
первые n компоненты дают оптимальный план
исходной задачи.
Теорема. Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача не имеет допустимых планов, т. е. ее условия несовместны.
3.1 Признаки оптимальности.
Теорема. Пусть исходная задача решается на максимум. Если для некоторого
опорного плана все оценки ![]()
![]() неотрицательны, то такой
план оптимален.
неотрицательны, то такой
план оптимален.
Теорема. Если исходная задача решается на
минимум и для некоторого опорного плана все оценки ![]()
![]() неположительны, то такой
план оптимален.
неположительны, то такой
план оптимален.
§4. Понятие двойственности.
Понятие двойственности рассмотрим на
примере задачи оптимального использования сырья. Пусть на предприятии решили
рационально использовать отходы основного производства. В плановом периоде
появились отходы сырья m
видов в объемах![]() единиц
единиц ![]() . Из этих отходов, учитывая
специализацию предприятия, можно наладить выпуск n видов неосновной продукции. Обозначим через
. Из этих отходов, учитывая
специализацию предприятия, можно наладить выпуск n видов неосновной продукции. Обозначим через ![]() норму расхода сырья i-го вида на единицу j-й
норму расхода сырья i-го вида на единицу j-й ![]() продукции,
продукции,
![]() - цена реализации единицы j-й продукции (реализация обеспечена).
Неизвестные величины задачи:
- цена реализации единицы j-й продукции (реализация обеспечена).
Неизвестные величины задачи: ![]() —
объемы выпуска j-й продукции,
обеспечивающие предприятию максимум выручки.
—
объемы выпуска j-й продукции,
обеспечивающие предприятию максимум выручки.
Математическая модель задачи:
![]() (1)
(1)
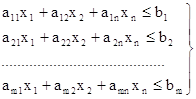 (2)
(2)
![]()
![]() (3)
(3)
Предположим
далее, что с самого начала при изучении вопроса об использовании отходов
основного производства на предприятии появилась возможность реализации их
некоторой организации. Необходимо установить прикидочные оценки (цены) на эти
отходы. Обозначим их ![]() .
.
Оценки должны быть установлены исходя из следующих требований, отражающих несовпадающие интересы предприятия и организации:
1) общую стоимость отходов сырья покупающая организация стремится минимизировать;
2) предприятие согласно уступить отходы только по таким ценам, при которых оно получит за них выручку, не меньшую той, что могло бы получить, организовав собственное производство.
Эти требования формализуются в виде следующей ЗЛП.
Требование 1 покупающей организации –
минимизация покупки: ![]() (4)
(4)
Требование 2 предприятия,
реализующего отходы сырья, можно сформулировать в виде системы ограничений.
Предприятие откажется от выпуска каждой единицы продукции первого вида, если ![]() , где левая часть означает
выручку за сырьё идущее на единицу продукции первого вида; правая – её цену.
, где левая часть означает
выручку за сырьё идущее на единицу продукции первого вида; правая – её цену.
Аналогичные рассуждения логично провести в отношении выпуска продукции каждого вида. Поэтому требование предприятия, реализующего отходы сырья, можно формализовать в виде сл. системы ограничений:
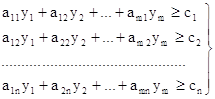 (5)
(5)
По смыслу задачи оценки не должны быть отрицательными:
![]() (6)
(6)
Переменные ![]()
![]() называют двойственными
оценками или объективно обусловленными оценками.
называют двойственными
оценками или объективно обусловленными оценками.
Задачи (1)-(3) и (4)-(6) называют парой взаимно двойственных ЗПЛ.
Между прямой и двойственной задачами можно установить следующую взаимосвязь:
1. Если прямая задача на максимум, то двойственная к ней — на минимум, и наоборот.
2. Коэффициенты ![]() целевой функции прямой
задачи являются свободными членами ограничений двойственной задачи.
целевой функции прямой
задачи являются свободными членами ограничений двойственной задачи.
3. Свободные члены ![]() ограничений прямой задачи
являются коэффициентами целевой функции двойственной.
ограничений прямой задачи
являются коэффициентами целевой функции двойственной.
4. Матрицы ограничений прямой и двойственной задач являются транспонированными друг к другу.
5. Если прямая задача на максимум, то ее
система ограничений представляется в виде неравенств типа ![]() . Двойственная задача
решается на минимум, и ее система ограничений имеет вид неравенств типа
. Двойственная задача
решается на минимум, и ее система ограничений имеет вид неравенств типа ![]() .
.
6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной — числу переменных прямой.
7. Все переменные в обеих задачах неотрицательны.
Теорема. Для любых допустимых планов ![]() и
и ![]() прямой и двойственной ЗЛП
справедливо неравенство
прямой и двойственной ЗЛП
справедливо неравенство ![]() , т.е.
, т.е.
![]() (7) – основное неравенство теории
двойственности.
(7) – основное неравенство теории
двойственности.
Теорема. (критерий оптимальности Канторовича)
Если для некоторых допустимых планов ![]() и
и ![]() пары двойственных задач
выполняется неравенство
пары двойственных задач
выполняется неравенство ![]() , то
, то ![]() и
и ![]() являются оптимальными
планами соответствующих задач.
являются оптимальными
планами соответствующих задач.
Теорема. (малая теорема двойственности)
Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
§5. Основные теоремы двойственности
и их экономическое содержание
Теорема.
Если одна из двойственных задач имеет
оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные
значения целевых функций равны: ![]() . Если
одна из двойственных задач неразрешима вследствие неограниченности целевой
функции на множестве допустимых решений, то система ограничений другой задачи
противоречива.
. Если
одна из двойственных задач неразрешима вследствие неограниченности целевой
функции на множестве допустимых решений, то система ограничений другой задачи
противоречива.
Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки, обладают тем свойством, что они гарантируют рентабельность оптимального плана, т. е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.
Теорема. (о дополняющей нежесткости )
Для того, чтобы планы ![]() и
и ![]() пары двойственных задач
были оптимальны, необходимо и достаточно выполнение условий:
пары двойственных задач
были оптимальны, необходимо и достаточно выполнение условий:
![]() (1)
(1)
![]() (2)
(2)
Условия (1), (2) называются условиями дополняющей нежесткости. Из них следует: если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
Экономически это
означает, что если по некоторому оптимальному плану ![]() производства
расход i -го ресурса строго меньше его запаса
производства
расход i -го ресурса строго меньше его запаса ![]() , то в оптимальном плане
соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же
в некотором оптимальном плане оценок его i -я компонента строго больше нуля, то в оптимальном
плане производства расход соответствующего ресурса равен его запасу. Отсюда
следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов.
Дефицитный ресурс (полностью используемый по оптимальному плану производства)
имеет положительную оценку, а ресурс избыточный (используемый не полностью)
имеет нулевую оценку.
, то в оптимальном плане
соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же
в некотором оптимальном плане оценок его i -я компонента строго больше нуля, то в оптимальном
плане производства расход соответствующего ресурса равен его запасу. Отсюда
следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов.
Дефицитный ресурс (полностью используемый по оптимальному плану производства)
имеет положительную оценку, а ресурс избыточный (используемый не полностью)
имеет нулевую оценку.
Теорема .(об оценках). Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи математического программирования, точнее
![]() (3)
(3)
§6. Примеры экономических задач
5.1 Задача о наилучшем использовании
ресурсов. Пусть
некоторая производственная единица (цех, завод, объединение и т. д.), исходя
из конъюнктуры рынка, технических или технологических возможностей и имеющихся
ресурсов, может выпускать n
различных видов продукции (товаров), известных под номерами, обозначаемыми
индексом j ![]() . Ее будем обозначать
. Ее будем обозначать ![]() . Предприятие при
производстве этих видов продукции должно ограничиваться имеющимися видами
ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов,
рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды
ограничивающих факторов называют ингредиентами
. Предприятие при
производстве этих видов продукции должно ограничиваться имеющимися видами
ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов,
рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды
ограничивающих факторов называют ингредиентами ![]() .
Пусть их число равно m;
припишем им индекс i
.
Пусть их число равно m;
припишем им индекс i ![]() . Они ограничены, и их количества
равны соответственно
. Они ограничены, и их количества
равны соответственно ![]() условных единиц.
Таким образом,
условных единиц.
Таким образом, ![]() - вектор ресурсов. Известна
экономическая выгода (мера полезности) производства продукции каждого вида,
исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам
производства, степени удовлетворения потребностей и т. д. Примем в качестве
такой меры, например, цену реализации
- вектор ресурсов. Известна
экономическая выгода (мера полезности) производства продукции каждого вида,
исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам
производства, степени удовлетворения потребностей и т. д. Примем в качестве
такой меры, например, цену реализации
![]()
![]() , т. е.
, т. е. ![]() —вектор
цен. Известны также технологические коэффициенты
—вектор
цен. Известны также технологические коэффициенты ![]() ,
которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов
,
которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов ![]() называют технологической и
обозначают буквой А. Имеем
называют технологической и
обозначают буквой А. Имеем ![]() .
Обозначим через
.
Обозначим через ![]() план производства,
показывающий, какие виды товаров
план производства,
показывающий, какие виды товаров ![]() нужно
производить и в каких количествах, чтобы обеспечить предприятию максимум
объема реализации при имеющихся ресурсах.
нужно
производить и в каких количествах, чтобы обеспечить предприятию максимум
объема реализации при имеющихся ресурсах.
Так как ![]() -
цена реализации единицы j'-й
продукции, цена реализованных
-
цена реализации единицы j'-й
продукции, цена реализованных ![]() единиц
будет равна
единиц
будет равна ![]() , а общий объем реализации
, а общий объем реализации![]()
Это выражение — целевая функция, которую нужно максимизировать.
Так как ![]() -
расход i-го ресурса на производство
-
расход i-го ресурса на производство ![]() единиц j-й продукции, то, просуммировав расход
i-го ресурса на выпуск всех n видов продукции, получим общий расход
этого ресурса, который не должен превосходить
единиц j-й продукции, то, просуммировав расход
i-го ресурса на выпуск всех n видов продукции, получим общий расход
этого ресурса, который не должен превосходить ![]()
![]() единиц:
единиц:
![]()
Чтобы искомый план ![]() был реализован, наряду с
ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы
был реализован, наряду с
ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы ![]() выпуска продукции:
выпуска продукции:
![]()
![]() .
.
Таким образом, модель задачи о наилучшем использовании ресурсов примет вид:
![]() (1)
(1)
при ограничениях:
![]()
![]() (2)
(2)
![]()
![]() (3)
(3)
Так как переменные ![]() входят в функцию
входят в функцию ![]() и систему ограничений
только в первой степени, а показатели
и систему ограничений
только в первой степени, а показатели ![]() являются
постоянными в планируемый период, то (1)-(3) – задача линейного
программирования.
являются
постоянными в планируемый период, то (1)-(3) – задача линейного
программирования.
5.2 Задача о смесях.
В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходных материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе задач относятся задачи о выборе диеты, составлении кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности, смесей для получения бетона в строительстве и т. д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.
5.3 Задача о раскрое материалов.
Сущность задачи об оптимальном раскрое состоит в разработке таких технологически допустимых планов раскроя, при которых получается необходимый комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму. Рассмотрим простейшую модель раскроя по одному измерению. Более сложные постановки ведут к задачам целочисленного программирования.
5.4 Транспортная задача.
Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям; при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. Так как от схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.
5.5 Задача о размещении заказа.
Речь идет о задаче распределения заказа (загрузки взаимозаменяемых групп оборудования) между предприятиями (цехами, станками, исполнителями) с различными производственными и технологическими характеристиками, но взаимозаменяемыми в смысле выполнения заказа. Требуется составить план размещения заказа (загрузки оборудования), при котором с имеющимися производственными возможностями заказ был бы выполнен, а показатель эффективности достигал экстремального значения.
§7. Анализ задачи об оптимальном использовании сырья.
Исходя из специализации и своих технологических возможностей предприятие может выступать четыре вида продукции. Сбыт любого количества обеспечен. Для изготовления этой продукции используются трудовые ресурсы, полуфабрикаты и станочное оборудование. Общий объём ресурсов, расход каждого ресурса за единицу продукции, приведены в таблице 1. Требуется определить план выпуска, доставляющий предприятию максимум прибыли. Выполнить после оптимизационный анализ решения и параметров модели.
| Ресурсы | Выпускаемая продукция |
Объём Ресурсов |
|||||||
|
|
|
|
|
||||||
|
|
Трудовые ресурсы, чел-ч | 4 | 2 | 2 | 8 | 4800 | |||
|
|
Полуфабрикаты, кг | 2 | 10 | 6 | 0 | 2400 | |||
|
|
Станочное оборудование, станко-ч | 1 | 0 | 2 | 1 | 1500 | |||
| Цена единицы продукции, р. | 65 | 70 | 60 | 120 |
|
||||
Решение.
Пусть ![]() -
объёмы продукции
-
объёмы продукции ![]() планируемый к
выпуску;
планируемый к
выпуску; ![]() - сумма ожидаемой выручки.
- сумма ожидаемой выручки.
Математическая модель пря мой задачи:
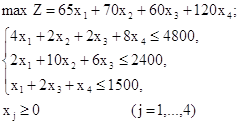
Математическая модель двойственной задачи:
![]()
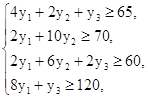
![]()
По условиям примера найти:
1. Ассортимент выпускаемой продукции, обеспечивающий предприятию максимум реализации (максимум выручки)
2. Оценки ресурсов, используемых при производстве продукции.
Симплексным методом решаем прямую задачу, модель которой составлена выше в таблице1.
После второй итерации все оценки
оказались отрицательными, значит, найденный опорный план является оптимальным: ![]() ,
, ![]()
Основные переменные ![]() показывают, что продукцию
показывают, что продукцию![]() и
и ![]() выпускать нецелесообразно,
а продукции
выпускать нецелесообразно,
а продукции ![]() следует произвести 400 ед.,
следует произвести 400 ед.,
![]() - 500 ед.
- 500 ед.
Дополнительные переменные ![]() и
и ![]() показывают, что ресурсы
используются полностью
показывают, что ресурсы
используются полностью ![]() , а вот равенство
, а вот равенство ![]() свидетельствует о том, что
200 единиц продукции
свидетельствует о том, что
200 единиц продукции ![]() осталось
неиспользованным.
осталось
неиспользованным.
| Номера ит. | БП | Сб |
|
|
|
|
|
|
|
|
| 65 | 70 | 60 | 120 | 0 | 0 | 0 | ||||
| 0 |
|
0 | 4800 | 4 | 2 | 2 | 8 | 1 | 0 | 0 |
|
|
0 | 2400 | 2 | 10 | 6 | 0 | 0 | 1 | 0 | |
|
|
0 | 1500 | 1 | 0 | 2 | 1 | 0 | 0 | 1 | |
|
|
0 | -65 | -70 | -60 | -120 | 0 | 0 | 0 | ||
| 1 |
|
120 | 600 | 1/2 | 1/4 | 1/4 | 1 | 1/8 | 0 | 0 |
|
|
0 | 2400 | 2 | 0 | 6 | 0 | 0 | 1 | 0 | |
|
|
0 | 900 | 1/2 | -1/4 | 7/4 | 0 | -1/8 | 0 | 1 | |
|
|
72000 | -5 | -40 | -30 | 0 | 15 | 0 | 0 | ||
| 2 |
|
120 | 500 | 5/12 | -1/6 | 0 | 1 | 1/8 | -1/24 | 0 |
|
|
60 | 400 | 1/3 | 5/3 | 1 | 0 | 0 | 1/6 | 0 | |
|
|
0 | 200 | -1/12 | -19,6 | 0 | 0 | -1/8 | -7/24 | 1 | |
|
|
84000 | 5 | 10 | 0 | 0 | 15 | 5 | 0 |
Выпишем из таблицы2. Компоненты
оптимального плана двойственной задачи – двойственные оценки. В канонической
форме прямой задачи переменные ![]() -
являются свободными, а дополнительные переменные
-
являются свободными, а дополнительные переменные ![]() -
базисными. В канонической форме двойственной задачи свободными будут переменные
-
базисными. В канонической форме двойственной задачи свободными будут переменные
![]() - а базисными
- а базисными ![]()
Соответствие между переменными примет вид
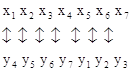
Учитывая это соответствие, выпишем из
индексной строки последней итерации компоненты искомого плана ![]() - двойственные оценки.
- двойственные оценки.
min f = max Z =84000.
Запишем это неравенство в развернутой форме:
48000*15 + 2400*5 + 1500*0 = 65*0 + 70*0 + 60*400 + 120*500
Учитывая, что компонеты представляют собой оценки ресурсов заключаем:
При оптимальном плане оценка ресурсов, затраченных на выпуск продукции, совпадает с оценкой произведенной продукции.
Теперь установим степень дефицитности используемых ресурсов и обоснуем рентабельность оптимального плана.
Мы нашли оптимальный план ![]() выпуска продукции. При этом
плане третье ограничение прямой задачи выполняется как строгое неравенство:
выпуска продукции. При этом
плане третье ограничение прямой задачи выполняется как строгое неравенство:
0+2-400+500= 1300< 1500. Это
означает, что расход ресурса ![]() меньше
его запаса, т. е. ресурс
меньше
его запаса, т. е. ресурс ![]() избыточный.
Именно поэтому в оптимальном плане
избыточный.
Именно поэтому в оптимальном плане ![]() двойственной
задачи оценка
двойственной
задачи оценка ![]() этого ресурса
равна нулю.
этого ресурса
равна нулю.
А вот оценки ![]() и
и ![]() ресурсов
ресурсов ![]() и
и ![]() выражаются положительными
числами 15 и 5, что свидетельствует о дефицитности этих ресурсов: они при
оптимальном плане используются полностью. В самом деле, ограничения по этим
ресурсам выполняются как строгие равенства: 4.0+2.0+2.400+8.500=4800,
2-0+10.0+6.400=2400.
выражаются положительными
числами 15 и 5, что свидетельствует о дефицитности этих ресурсов: они при
оптимальном плане используются полностью. В самом деле, ограничения по этим
ресурсам выполняются как строгие равенства: 4.0+2.0+2.400+8.500=4800,
2-0+10.0+6.400=2400.
Поскольку 15>5, ресурс ![]() считается более дефицитным,
чем ресурс
считается более дефицитным,
чем ресурс ![]() .
.
На основе теоремы (о дополняющей
нежесткости) нетрудно объяснить, почему не вошла в оптимальный план продукция ![]() и
и ![]() : первое и второе
ограничения двойственной задачи выполняются как строгие неравенства:
4-15+2-5+0>65, 2-15+10*5>70.
: первое и второе
ограничения двойственной задачи выполняются как строгие неравенства:
4-15+2-5+0>65, 2-15+10*5>70.
Это означает, что оценки ресурсов,
расходуемых на изготовление единицы продукции ![]() и
и
![]() , превышают оценки единицы
этой продукции. Понятно, что такую продукцию выпускать предприятию невыгодно.
Что же касается продукции
, превышают оценки единицы
этой продукции. Понятно, что такую продукцию выпускать предприятию невыгодно.
Что же касается продукции ![]() и
и ![]()
![]() , то выпуск ее оправдан, поскольку оценка израсходованных
ресурсов совпадает с оценкой произведенной продукции: 2*15+ +6*5+2*0=60, 8*15+0=120.
, то выпуск ее оправдан, поскольку оценка израсходованных
ресурсов совпадает с оценкой произведенной продукции: 2*15+ +6*5+2*0=60, 8*15+0=120.
Таким образом, в оптимальный план войдет только та продукция, которая выгодна предприятию, и не войдет убыточная продукция. В этом проявляется рентабельность оптимального плана.
Рассмотрим возможность дальнейшего совершенствования оптимального ассортимента выпускаемой продукции.
Выше установлено, что ресурсы ![]() и
и ![]() являются дефицитными. В
связи с этим на основе теоремы (об оценках) можно утверждать, что на каждую
единицу ресурса
являются дефицитными. В
связи с этим на основе теоремы (об оценках) можно утверждать, что на каждую
единицу ресурса ![]() , введенную
дополнительно в производство, будет получена дополнительная выручка
, введенную
дополнительно в производство, будет получена дополнительная выручка ![]() , численно равная
, численно равная ![]() . В самом деле, при
. В самом деле, при ![]() получаем
получаем ![]() . По тем же причинам каждая
дополнительная единица ресурса
. По тем же причинам каждая
дополнительная единица ресурса![]() обеспечит
прирост
обеспечит
прирост ![]() выручки, равный 5 р. Теперь
становится понятно, почему ресурс
выручки, равный 5 р. Теперь
становится понятно, почему ресурс ![]() считается
более дефицитным по сравнению с ресурсом
считается
более дефицитным по сравнению с ресурсом ![]() :
он может содействовать получению большей выручки.
:
он может содействовать получению большей выручки.
Что же касается
избыточного ресурса ![]() , то
увеличение его запаса не приведет к росту выручки, поскольку
, то
увеличение его запаса не приведет к росту выручки, поскольку ![]() . Из приведенных
рассуждений следует, что оценки ресурсов позволяют совершенствовать план
выпуска продукции.
. Из приведенных
рассуждений следует, что оценки ресурсов позволяют совершенствовать план
выпуска продукции.
Выясним экономический смысл оценок ![]() продукции
продукции ![]() ,
,![]() ,
,![]() ,
,![]() .
.
По оптимальному плану ![]() выпускать следует продукцию
выпускать следует продукцию ![]() и
и ![]() . Оценки
. Оценки ![]() и
и ![]() этих видов продукции равны
нулю. Что это означает, практически станет ясно, если представить оценки в
развернутой записи:
этих видов продукции равны
нулю. Что это означает, практически станет ясно, если представить оценки в
развернутой записи:
![]()
![]()
Таким образом, нулевая оценка показывает, что эта продукция является неубыточной, поскольку оценка ресурсов, расходуемых на выпуск единицы такой продукции, совпадает с оценкой единицы изготовленной продукции.
Что же касается продукции
![]() и
и ![]() являющейся, как установлено
выше, убыточной, а потому и не вошедшей в оптимальный план, то для ее оценок
являющейся, как установлено
выше, убыточной, а потому и не вошедшей в оптимальный план, то для ее оценок ![]() и
и ![]() получаем:
получаем:
![]()
![]()
Отсюда видно, что оценка убыточной продукции показывает, насколько будет снижать каждая единица такой продукции достигнутый оптимальный уровень.
§8. Программа и расчеты.
{Программа составлена для решения задачи линейного программирования
симплексным методом}
uses crt;
const n=2;{число неизвестных исходной задачи}
m=3;{число ограничений}
m1=0;{последняя строка равенств}
m2=1;{последняя строка неравенств вида >=}
label 5,15,20,10;
var b,cb:array[1..m] of real;c,x,e:array[1..50] of real;a:array[1..m,1..50] of real;
s0,max,mb,s1:real;i,j,k,i0,j0,m21,nm1,n1:integer; Bi:array[1..m] of integer;
begin
clrscr;
writeln;
writeln (' Симплексный метод решения задачи линейного программирования:');
writeln;
writeln (' Проведем некоторые преобразования с данной задачей:');
writeln;
writeln (' Подготовьте матрицу: сначала равенства, потом неравенства вида >= и неравенства вида <=;');
writeln (' Целевая функция должна быть на минимум (привести ее к такому виду); ');
writeln (' Вектор b должен состоять только из положительных элементов (привести его к та- кому виду);');
writeln(' Введите матрицу А ',m,'*',n,' построчно:');
for i:=1 to m
do begin for j:=1 to n
do read (a[i,j]);
readln
end;
writeln (' Введите в виде строки вектор b, состоящий из ',m,' компонент:');
for i:=1 to m
do read (b[i]);
writeln(' Введите теперь вектор с, состоящий из ',n,' компонент:');
for i:=1 to n
do read (c[i]);
m21:=m2-m1+n;nm1:=n+m-m1;n1:=n+m-m1+m2;
for i:=1 to m
do for j:=n+1 to n1
do a[i,j]:=0;
{переход к равенствам в неравенствах >=}
for i:=m1+1 to m2
do a[i,n+i-m1]:=-1;
{переход к равенствам в неравенствах <=}
for i:=m2+1 to m
do a[i,m21+i-m2]:=1;
{создание искуственного базиса}
for i:=1 to m2
do a[i,nm1+i]:=1;
{ввод mb в вектор с}
mb:=12345;
for i:=n+1 to nm1
do c[i]:=0;
for i:=nm1+1 to n1
do c[i]:=mb;
{выписать cb}
for i:=1 to m2
do begin cb[i]:=mb; Bi[i]:=nm1+i end;
for i:=m2+1 to m
do begin Bi[i]:=m21+i-m2;
cb[i]:=0;
end;
for i:=1 to n1
do x[i]:=0;
writeln(' Решение задачи:');
{применяем симплексный метод, вычисляем оценки}
5: for j:=1 to n1
do begin s0:=0;
for i:=1 to m
do s0:=s0+cb[i]*a[i,j];
e[j]:=s0-c[j]
end;
max:=e[1];j0:=1;
for i:=2 to n1
do if e[i]>max
then begin max:=e[i];
j0:=i
end;
{получили столбец с максимальной оценкой}
if max<=0
then begin for i:=1 to m
do x[Bi[i]]:=b[i];
goto 15
end;
s1:=a[1,j0];
for i:=2 to m
do if s1<a[i,j0]
then s1:=a[i,j0];
if s1<=0
then goto 10;
s1:=mb;
for i:=1 to m
do if a[i,j0]>0
then if s1>b[i]/a[i,j0]
then begin
s1:=b[i]/a[i,j0];
i0:=i
end;
{главный элемент a[i0,j0]}
s0:=a[i0,j0]; Bi[i0]:=j0;
for j:=1 to n1
do a[i0,j]:=a[i0,j]/s0;
b[i0]:=b[i0]/s0;
for i:=1 to m
do if i<>i0
then begin s1:=-a[i,j0];
b[i]:=b[i]+b[i0]*s1;
for j:=1 to n1
do a[i,j]:=a[i,j]+a[i0,j]*s1
end;
cb[i0]:=c[j0];
goto 5;
10: writeln(' Нет оптимального плана, функция неограничена');
goto 20;
{просмотр иск. переменных}
15: for i:=nm1+1 to n1
do if x[i]>0
then begin writeln(' Пустое множество планов');
goto 20
end;
for i:=1 to n
do writeln(' x[',i,']=',x[i]:7:4);
20:readkey
end.
Содержание
Введение………………………………………………………………………………1
§1. Задача линейного программирования и свойства её решений…………….…4
§2. Графический способ решения
задачи линейного программирования……………………………………….…6
§3. Симплексный метод……………………………………………………………..8
§4. Понятие двойственности……………………………………………………….11
§5. Основные теоремы двойственности
и их экономическое содержание………………………………………….……14
§6. Примеры экономических задач………………………………………………..16
§7. Анализ задачи об оптимальном использовании сырья………………………19
§8. Программа и расчеты…………………………………………………………..25