Реферат: Математическое моделирование в сейсморазведке
Лекция 1
Введение
Метод математического моделирования получил распространение в сейсморазведке примерно с середины 60-х годов. Использование синтетических сейсмограмм (СС), являвшихся результатом решения одномерной динамической задачи, имело следующий цели:
· анализ процесса формирования поля отраженных волн в тонкослоистой среде;
· оценку роли многократных волн в этом поле;
· определение сейсмических эффектов, обусловленных изменением литологии или углеводородосодержания и др.
В целом это позволило получить важные для практики интерпретации выводы о том, какие особенности и признаки нужно искать на реальной сейсмозаписи при изучении того или иного геологического объекта.
Переход к двумерному сейсмическому моделированию, т. е. к использованию синтетических временных разрезов (СВР), означал не просто увеличение количества синтезируемых трасс, а качественно новый уровень реализации метода моделирования. Речь идет об открывшейся возможности применения математического моделирования непосредственно в процессе интерпретации данных сейсмических наблюдений
К началу 80-х годов сложилась следующая классификация видов сейсмомоделирования.
1. Структурное моделирование. Обычно такое моделирование осуществляется путем прослеживания лучей, что позволяет воспроизвести истинный путь сейсмических волн при пересечении границ напластований, установить точную связь между временем и глубиной и понять причины своеобразного отображения определенных структурных форм на временном разрезе. С помощью структурного моделирования могут производиться оценка и учет влияния вышележащих толщ на кинематику сейсмических волн в интересующем (перспективном) диапазоне времен или глубин при решении стратиграфических задач.
2. Стратиграфическое моделирование. Первоначально применялось с целью получить оценку влияния залежей нефти и газа, выклинивающихся слоев, зон литолого-фациального замещения и других неоднородностей на такие характеристики сейсмической записи, как изменение амплитуд, искажение вышезалегающих горизонтов, изменение полярности, понижение скорости, наличие и расположение дифрагированных волн. Структурные формы здесь менее важны, а упругие параметры горных пород, наоборот, являются очень важными и решающими. В последнее время стратиграфическое моделирование успешно применяется для обнаружения и подтверждения залежей углеводородов, определения литологии пород, связанных с этими залежами, границ распространения залежей и др.
3. Моделирование сейсмических скоростей. Вначале такое моделирование получило распространение в связи с необходимостью оценки влияния кривизны отражающих и промежуточных границ и локальных неоднородностей на поле сейсмических скоростей или, другими словами, для анализа отклонений параметра VОГТ реальных скоростей в среде. Впоследствии были осуществлены удачные опыты использования этого вида моделирования в качестве основы в методах решения обратных кинематических задач для многослойных сред с криволинейными границами раздела и с градиентами скоростей в слоях.
Кроме того, двумерное сейсмомоделирование стало эффективно использоваться и на этапе обработки сейсмической информации для решения таких задач, как:
· расчет статических и кинематических поправок в условиях неоднородностей в верхней части разреза,
· тестирование новых программно-алгоритмических средств,
· синтез оптимальных графов обработки.
Глава 1. Общие принципы интерпретации данных сейсморазведки на основе математического моделированияРаздел 1.1. Системный анализ проблемы интерпретации данных сейсмических наблюдений
В соответствии с методологическим принципом системного подхода представим объект нашего изучения (процесс интерпретации данных сейсмических наблюдений) в виде целостной системы взаимодействующих элементов (верхняя часть рис. 1, а).
Будем называть интерпретацией данных сейсмических наблюдений процесс построения сейсмогеологической модели, которая не противоречит имеющейся априорной информации (наблюденному волновому полю, данным промысловой геофизики, геологической информации) и опыту геофизика-интерпретатора. Из этого определения следует несколько важных методологических выводов:
1) процесс интерпретации является целенаправленным и поэтому должен быть управляемым;
2) в процессе интерпретации необходимо сопоставлять имеющуюся в данный момент сейсмогеологическую модель с априорными данными (в первую очередь с наблюденным волновым полем) на предмет анализа их противоречивости и нахождения способов ее устранения;
3) ввиду невозможности непосредственного сопоставления таких разнородных объектов, как сейсмогеологическая модель и наблюденное волновое поле, в процессе интерпретации необходимо решать прямую задачу, т.е. вычислять волновое поле по сейсмогеологической модели.
Таким образом, математическое моделирование становится неотъемлемой частью технологии интерпретации.
Конкретизируя схему рис. 1, а, получаем схему интерпретации данных сейсморазведки на основе математического моделирования, представленную на рис. 1, б. Она включает операции шести уровней.
I уровень – получение исходной информации в результате геофизических измерений и сбора априорных геологических данных.
II уровень – обработка и анализ указанной информации с различными целями. Полевые данные сейсморазведки обрабатываются в целях получения
- годографов;
§ горизонтальных спектров скоростей или графиков VОГТ;
- окончательного временного разреза, который должен содержать минимум помех и искажений и максимум объективной информации о строении среды.
Данные промысловой геофизики обрабатываются главным образом для получения эффективной по сейсмическим критериям одномерной сейсмической модели. Наконец, важнейшую роль, определяющую впоследствии все решения геофизика-интерпретатора, играет предварительно выработанная гипотеза о строении разреза, не противоречащая имеющимся геологическим представлениям.
III уровень состоит в создании исходной для итеративного процесса интерпретации двумерной сейсмогеологической модели или модели нулевого приближения. Эта операция в принципе неформальна и требует максимального использования всей доступной информации I и II уровней. На этом же уровне производится выбор импульса, моделирующего сейсмический сигнал (моделирование сейсмического сигнала).
На IV уровне для получения модельных аналогов промежуточных и окончательных результатов обработки полевых данных сейсморазведки решаются прямые задачи сейсморазведки.
V уровень – операции сравнения промежуточных и окончательных результатов обработки с их модельными аналогами, имеющие целью количественную оценку сходства между ними.
VI уровень в рассматриваемой схеме представляют процессы принятий по коррекции параметров в общем случае всех операций уровней II–V. В частности, при наименее "глубокой" обратной связи корректируются параметры сейсмомоделирования, т. е. сейсмогеологическая модель и модель импульса падающей волны. Исходными данными для принятия таких решении являются оценки сходства ("рассогласования"), получаемые на уровне V.
Раздел 1.2. Теоретические вопросы автоматизированной интерпретации данных сейсморазведки
|
Лекция 2 |
Таблица
1. Влияние параметров двумерного сейсмомоделирования
на характеристики отражений
|
Кинематические и |
Параметры |
|
А. Определяемые по отдельным трассам синтетического временного разреза |
|
| 1. Время отражения |
1. Локальные мощности пластов вышележащей толщи 2. Локальные скорости в пластах вышележащей толщи 3. Геометрия отражающей и промежуточных границ |
| 2. Амплитуда отражения |
1. Дифференциация скоростей и плотностей соседних слоев 2. Мощности слоев 3. Количество слоев, участвующих в формировании отраженной волны 4. Геометрия отражающей и промежуточных границ 5. Частота исходного сигнала |
| 3. Преобладающая частота отражения |
1. Частота исходного сигнала 2. Мощности слоев 3. Количество слоев, участвующих в формировании отраженной волны 4. Величины частотно-зависимого коэффициента поглощения |
| 4. Полярность отражения |
1. Полярность исходного сигнала 2. Порядок чередования слоев 3. Тип насыщающего флюида |
|
5. Форма отражения: а) длительность волны, выраженная количеством фаз |
1. Количество слоев, участвующих в формировании отраженной волны 2. Мощности слоев 3. Ширина спектра исходного сигнала 4. Частота исходного сигнала |
| б) соотношение амплитуд экстремумов (форма огибающей) |
1. Форма огибающей исходного сигнала 2. Количество слоев, участвующих в формировании отраженной волны 3. Дифференциация скоростей и плотностей соседних слоев 4. Мощности слоев |
|
Б. Определяемые по синтетическому временному разрезу |
|
|
6. Поведение линий t0 |
1. Геометрия отражающей и промежуточных границ 2. Скорости и величины их градиентов в пластах вышележащей толщи 3. Мощности пластов вышележащей толщи |
|
7. Интерференция а) изменение времени между соседними фазами отражения |
1. Градиент изменения мощностей слоев, участвующих в формировании отраженной волны 2. Градиент изменения скоростей слоев, участвующих в формировании отраженной волны |
| б) изменения амплитуды отдельных фаз отражения (изменение формы огибающей) |
1. Градиент изменения плотностей слоев, участвующих в формировании отраженной волны 2. Криволинейность границ, участвующих в формировании отраженной волны |
| 8. Когерентность |
1. Градиент изменения мощностей слоев, участвующих в формировании отраженной волны 2. Градиент изменения скоростей слоев, участвующих в формировании отраженной волны 3. Градиент изменения плотностей слоев, участвующих в формировании отраженной волны 4. Криволинейность границ, участвующих в формировании отраженной волны |
| 9. Расположение и интенсивность дифрагированных волн |
1. Наличие и местоположение объектов дифракции (точки выклинивания, примыкания; тектонические нарушения; резкие перегибы слоев, радиус кривизны которых меньше длины волны; участки резкого изменения пластовых параметров и т. п.) 2. Дифференциация скоростей и плотностей в дифрагирующих телах и вмещающих породах |
Предметом нашего рассмотрения являются волновые поля, образующиеся в многослойных средах в случае применения источника, возбуждающего преимущественно продольные волны, наблюдения отраженных волн при достаточно малых углах падения на границы раздела и регистрации только вертикальных компонент смещения. При моделировании таких волновых полей достаточно задавать в слоях модели следующие параметры: скорость продольных волн Vp, плотность s и коэффициент поглощения продольных волн ap. Поле продольных отраженных волн будет определяться в этом случае только данными параметрами, а распределение параметров поперечных волн не будет играть существенной роли. Вследствие допущения о малых углах падения волны на границы раздела анизотропия скоростей также не учитывается.
В большинстве случаев для построения двумерных моделей используется информация двух видов: высокоточная, но разреженная по площади геолого-геофизическая информация по разведочным скважинам и менее точная, но существенно более плотная сейсмическая информация между скважинами. Первая позволяет получить достоверные оценки физических свойств разреза в отдельных точках, т. е. построить одномерные модели. С помощью второй информации осуществляется переход к двумерным моделям.
Раздел 2.1. Построение одномерных моделей
Исходная информация, т. е. значения детальных скоростей и плотностей, для построения одномерных тонкослоистых моделей может быть получена несколькими способами:
1. По данным акустического (АК), гамма-гамма (ГГК) или гравитационного каротажей после соответствующей их обработки; обработка АК обычно включает процедуры вычисления скоростей с учетом кавернометрии, коррекции полученных скоростей по сейсмическому каротажу (СК), осреднения и др.; ГГК дает сразу плотность, поэтому обработка его заключается только в осреднении.
2. При отсутствии АК или ГГК, а также при низком их качестве акустические свойства разреза прогнозируются с использованием других широко распространенных промыслово-геофизических характеристик: кажущегося сопротивления (rk), интенсивности первичного (ГК) и вторичного (НГК) гамма-излучения и др.
3. Для приближенного задания акустических параметров тонких слоев иногда используются нормальные или обобщенные зависимости скорости и плотности от глубины для пород различной литологии.
Кроме того, информация о детальном распределении скоростей и плотностей в разрезе может быть получена по данным изучения керна, однако эти данные следует использовать только в тех случаях, если измерения проводились в условиях, близких к пластовым.
Из перечисленных способов предпочтение следует отдать использованию данных АК и ГГК.
Осреднение данных АК и ГГК
Большое количество данных АК, накопленное к настоящему времени, подтверждает представления о тонкослоистой структуре реального скоростного разреза. Практически все осадочные породы, за редким исключением (чистая соль, лед), имеют тонкослоистую структуру с той или иной степенью скоростной дифференциации.
Исходные непрерывные скоростные и плотностные разрезы, характеризующиеся высокой детальностью, не могут быть приняты в качестве одномерных моделей, по которым в дальнейшем предстоит построить двумерную модель. Тем или иным способом производится их осреднение и построение максимально упрощенной однородно-слоистой (или тонкослоистой) модели среды. Такая модель представляется в виде серии тонких однородных пластов, разделенных границами первого рода. При построении тонкослоистых моделей предполагается, что акустическая неоднородность, обусловленная внутренней изменчивостью пород пласта, незначительна по сравнению с межпластовой акустической неоднородностью, связанной с изменением литологии или типа насыщения.
Способ осреднения с порогом. Применение его позволяет получить тонкослоистую модель в виде серии однородных слоев большей мощности по сравнению с исходным разрезом. Все границы в модели представляются границами первого рода. Сущность алгоритма осреднения в данном способе заключается в том, что по заданным DV – величине значимой скоростной дифференциации и Dqmin – минимальной временной мощности слоев из разреза исключаются тонкие слои, время пробега в которых dti < Dqmin, объединяются слои с номерами i и i-1, если разница скоростей в них удовлетворяет условию
|Vi – Vi–1| £ DV
Значение скорости в объединенном слое вычисляется как среднее из Vi и Vi-1. Пороговое значение скачка скорости DV может быть различным для разных частей разреза.
Изменяя DV, можно менять число слоев в модели N, так как оно тем меньше, чем больше DV. Это может быть использовано для автоматического поиска моделей с числом слоев, находящихся в заданных пределах Nmin – Nmax.
Раздел 2.2. Построение двумерных моделей
Рассмотрим методику построения двумерных сейсмогеологических моделей, представляющих собой комбинацию толстослоистых толщ (покрывающей и подстилающей) и собственно моделируемого интервала в виде совокупности тонких слоев. Чтобы условия интерференции волн на верхней и нижней границах моделируемого интервала не отличались от реальных, необходимо этот интервал расширить вверх и вниз на величину не менее l (длина волны). Пример комбинированной модели представлен на рис. 8, д.
Такие модели используются, как правило, при решении стратиграфических задач, в которых объектами исследования могут быть зоны выклинивания и фациального замещения, залежи углеводородов и др. При этом моделируемый интервал должен совпадать с объектом исследований. Желательно, чтобы в пределах моделируемого профиля имелось две-три опорные точки, в которых по данным глубоких скважин заданы одномерные модели. Когда на профиле или вблизи него нет глубоких скважин, то в принципе возможно построение достаточно детальных моделей только по данным сейсморазведки.
Выбор комбинированного типа моделей для описания способов построения самых разнообразных в целевом отношении двумерных моделей оправдан тем, что:
· во-первых, такая модель получила наибольшее распространение в практике моделирования и,
· во-вторых, излагаемые ниже способы пригодны как для построения толстослоистых моделей (используемых при решении прямых и обратных кинематических задач), так и для построения тонкослоистых моделей по всему разрезу (используемых при решении прямых и обратных динамических задач).
Однако на практике последние строятся очень редко из-за крайней трудоемкости построения таких моделей в двумерном варианте. Поэтому тонкими слоями задается ограниченный интервал, т. е. и в этом случае приходится иметь дело с комбинированной моделью.
При построении покрывающей толстослоистой части комбинированной модели, как правило, используется традиционный сейсмический разрез. При этом желаемым является условие: форма границ и значения скоростей в пластах должны быть такими, чтобы сохранялись кинематические годографы основных отраженных волн, а границам приписаны те коэффициенты отражения, которые получаются при расчетах с учетом их тонкослоистой структуры при определенной форме волны. В некоторых случаях покрывающая толща может задаваться в виде одного или двух пластов с эффективными параметрами или с искусственно подбираемыми скоростями и толщинами, при которых совпадали бы времена отражений на синтетическом и реальном временных разрезах в пределах моделируемого интервала
§ 2.2.1. Построение модели по данным бурения
При отсутствии данных сейсморазведки, т. е. в задачах предварительной оценки сейсмических аномалий, обусловленных особенностями геологического строения разреза (нефтегазоносность, фациальные замещения, выклинивания и др.), двумерные модели наиболее просто строятся путем линейной интерполяции свойств среды и положения границ в области между разведочными скважинами.
Метод линейной интерполяции достаточно точен в том случае, если период изменений используемых для моделирования геолого-геофизических характеристик больше расстояния между скважинами. В подавляющем большинстве случаев это условие не выполняется, и линейная интерполяция является лишь наиболее простым решением из множества вариантов увязки одномерных моделей по соседним скважинам.
|
Лекция 3 |
§ 2.2.2. Построение моделей по данным бурения и сейсморазведки
Наличие сейсмических временных разрезов позволяет отказаться от линейной интерполяции и осуществить построение модели с помощью следующих приемов:
1. Производится тщательная стратиграфическая привязка отраженных волн в точках глубоких скважин, причем наиболее надежная привязка осуществляется по временному разрезу, в который "врезаны" диаграммы скорости по АК в масштабе двойного времени и синтетические сейсмограммы.
2. На сейсмическом разрезе границы путем параллельного переноса точно совмещаются в точках расположения скважин с теми геологическими границами, которые определены в результате стратиграфической привязки (см. п. 1) как доминирующие при формировании отраженной волны. Если по какой-либо скважине получается невязка, то она "разбрасывается" по линейному закону в глубины сейсмической границы между скважинами.
3. На полученный в результате такой коррекции сейсмический разрез, который можно назвать базисной толстослоистой моделью, в точках расположения скважин наносятся тонкослоистые модели, соответствующие моделируемому интервалу. В пределах моделируемого интервала проводятся границы отдельных литологически однородных тонких слоев. При этом в зависимости от предполагаемой степени сложности двумерной модели подходы к ее построению могут быть различными. В зонах выдержанной корреляции сейсмических данных, которые, как правило, соответствуют согласному или близкому к нему залеганию пород, эти границы проводятся так, чтобы они соединяли отметки по скважинам и были параллельны сейсмическим границам между скважинами. Участки изменений сейсмических данных (схождение осей синфазности, изменения формы и интенсивностей колебаний, разрывы в корреляции) тщательно анализируются и с учетом данных по скважинам задаются возможные модели изменений мощности слоев, литолого-фациальных замещений, появления углеводородов и др. Нередки случаи, когда в пределах одного моделируемого интервала встречаются участки различной сложности.
4. Задаются упругие параметры (скорости и плотности) во всех слоях модели, при этом в точках между скважинами эти параметры находятся путем линейной интерполяции значений, полученных ранее в процессе формирования одномерных моделей в точках расположения скважин.
§ 2.2.3. Построение моделей по данным сейсморазведки
Если на профиле нет скважин, то модель может быть построена только по сейсмическим данным. В этом случае целесообразно применять такие процедуры.
1. На основе кинематической интерпретации временного разреза строится базисная толстослоистая модель. Используемые при этом средние и пластовые скорости берутся из данных скоростного анализа, а в условиях Волго-Уральской провинции – чаще из интерполированных или экстраполированных сейсмокаротажных данных.
2. Интервал временного разреза, соответствующий моделируемому объекту, преобразуется во временной разрез волновых сопротивлений по методике псевдоакустического каротажа (ПАК).
3. В ряде точек профиля строятся одномерные модели волновых сопротивлений. Затем от волновых сопротивлений с использованием формулы s =аVb, где s – плотность, V – скорость, переходят к оценкам скорости и плотности. Полученные таким способом одномерные модели скорости целесообразно проверять на соответствие со значениями пластовых скоростей, взятыми из интерполированных или экстраполированных сейсмокаротажных данных.
4. Одномерные тонкослоистые модели наносятся на базисную толсто-слоистую модель, после чего, так же как и в предыдущем параграфе, строится комбинированная двумерная модель.
Необходимо отметить, что из-за использования только сейсмических данных, имеющих ограниченный частотный диапазон, тонкослоистую часть комбинированной модели следует рассматривать как эффективную сейсмическую модель.
Если полученные по описанным выше методикам двумерные модели предполагается использовать для интерпретации в итеративном режиме, то их целесообразно называть моделями нулевого приближения (моделями 0-приближения).
§ 2.2.4. Влияние нефтегазонасыщенности на упругие свойства пород
Сведения об изменении упругих свойств (скорости и плотности) пород-коллекторов в зависимости от типа насыщающего флюида можно получить прямым измерением в скважинах, расположенных в контуре залежи и за контуром, изучением керна при различном его насыщении, путем теоретических расчетов.
Прямые измерения в скважинах с помощью сейсмического просвечивания и СК выполнены в ограниченном объеме и полученные результаты не всегда достаточно точны. Обобщение данных показывает, что в нефтенасыщенных песчаных коллекторах при глубинах 1500–3000 м и средней пористости 20% скорость продольных волн уменьшается на 6–12%, в газонасыщенных коллекторах – на 15–30% по сравнению с водонасыщенным коллектором.
При измерениях на ультразвуковых частотах (АК) величина различия скоростей, обусловленная водо- и нефтегазонасыщенностью пород, меньше, чем на сейсмических частотах. Поэтому использование данных об уменьшении скоростей при нефтегазонасыщении, полученных на ультразвуковых частотах (в скважинах или на образцах керна), для модельных расчетов в сейсмическом диапазоне частот возможно лишь после их коррекции. Удвоение величин понижения скорости будет, по-видимому, вполне допустимым. Данных об изменении плотности при различном насыщении коллектора, которые были бы получены путем прямых измерений в скважинах, пока не имеется.
При отсутствии данных прямых измерений на керне или в скважине (или если эти данные недостаточно надежны) влияние нефтегазонасыщения на скорость и плотность может быть оценено теоретически, с помощью формул из теории распространения упругих волн в пористых средах. Для определения скорости продольных волн в сейсмическом диапазоне частот используется уравнение
![]() ,
(2.1)
,
(2.1)
где Uп и sп – параметры, зависящие соответственно от упругости и плотности флюида; Uск и sск – параметры, характеризующие упругость и плотность скелета (остова) породы.
Значения U и s следующим образом выражаются через свойства твердого материала породы и насыщающего ее флюида:
1) sск = sтв (1 – Kп), где sтв – плотность материала, слагающего твердую фазу породы, Kп – пористость;
2) sп = sф Kп, где sф – плотность флюида, т. е. плотность воды, нефти, газа или их смеси;
3) ![]() , где bск – сжимаемость скелета
(относительное изменение объема скелета при всестороннем упругом сжатии
породы), Gск – модуль сдвига скелета;
, где bск – сжимаемость скелета
(относительное изменение объема скелета при всестороннем упругом сжатии
породы), Gск – модуль сдвига скелета;
4) 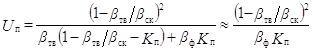
где bтв – сжимаемость материала, слагающего скелет породы, bф – сжимаемость флюида, величины bтв и bск связаны соотношением bск = bтв + Kпbп (bп – сжимаемость порового пространства).
При использовании формулы (2.1) основная трудность заключается в выборе величин bск и Gск.
Для приближенных расчетов можно использовать уравнение среднего времени (уравнение Уилли)
![]() , (2.2)
, (2.2)
где Vп – скорость в коллекторе, заполненном флюидом; Vск – скорость в скелете; Vф – скорость во флюиде, Kп – коэффициент пористости. Формула (2.2) справедлива для хорошо сцементированных пород. Величину плотности можно оценить по уравнению
sп = sск (1 – Kп) + sфKп, (2.3)
где sп – плотность коллектора, заполненного флюидом, sск – плотность скелета, sф – плотность флюида.
Если поры заполнены несколькими компонентами, например газ–вода, нефть–вода и т. д., то имеет место уравнение
sп = sск (1 – Kп) + sфKп + (sв – sф)SвKп,
где sв – плотность воды, Sв – коэффициент водонасыщенности.
Глава 3. Методика интерпретации на основе итеративного моделированияРаздел 3.1. Особенности получения и обработки сейсмических данных, интерпретируемых на основе моделирования
Главное требование, предъявляемое к данным сейсмических наблюдений, которые интерпретируются с помощью итеративного моделирования, состоит в повышенном отношении сигнал/помеха. Опыт сейсмомоделирования показывает, что нижний предел отношения энергии сигнала к энергии помехи, равный 10 – 15, является достаточным для того, чтобы в процессе итеративного подбора параметров модели достичь достаточно высокую степень сходства СВР и реального временного разреза (РВР). Это предельное значение установлено на основе тестового моделирования и сопоставления СВР и РВР по нормированной функции взаимной корреляции (НФВК) и значений отношения сигнал/помеха на РВР по одинаковым фрагментам временных разрезов. На рис. 4 показан пример такого сопоставления по профилю 39 Северо-Маркинской площади, из которого видно, что сходство СВР и РВР до 0,8 и выше удавалось получить только на участках, где отношение сигнал/помеха на РВР достигало 10 – 15 и выше.
Важным является также требование иметь на реальных временных разрезах достаточно высокую временную разрешенность отражений. При повышении разрешенности появляется возможность не только более детально, т.е. в более узких временных окнах, производить сравнение СВР и РВР и последующую коррекцию модели, но и получать более детальные псевдоакустические разрезы, необходимые для построения модели 0-приближения.
|
Лекция 4 |
Достижение подобного качества РВР естественно накладывает более жесткие требования на методику полевых наблюдений и последующую обработку сейсмических данных.
§ 3.1.1. Методика полевых наблюдений
Как известно, требования повышения отношения сигнал/помеха и увеличения разрешенности записи в какой-то мере противоречивы. Поэтому на практике важно определить, какое из этих требований является доминирующим при изучении того или иного геологического объекта. Например, при изучении рифогенных построек, грабенообразных прогибов и др. прежде всего нужно обеспечить высокое отношение сигнал/помеха, а при выявлении зон выклинивания и стратиграфического несогласия, первостепенным становится требование высокой разрешенности сейсмической записи.
На поисковом этапе исследований, в целях выявления рифогенных образований, грабенообразных прогибов, выступов кристаллического фундамента методика полевых работ может быть близка к производственной или отличаться от нее некоторым увеличением мощности интерференционных систем при возбуждении и приеме. Основные элементы такой методики следующие:
1) плотность сети профилей 1,5–2,0 пог. км на 1 км2;
2) схема наблюдения – в основном центральная;
3) кратность перекрытия 12 или 24;
4) максимальное расстояние взрыв – прибор Хmax = 1700–2500 м;
5) вынос 25–200 м;
6) расстояние между каналами 40–50 м;
7) группирование сейсмоприемников до 36 на канал, причем расположение приемников в одну или две линии на базе не более 50 м;
8) возбуждение – взрывы в одиночных скважинах с оптимальной глубины или из группы мелких (4–5 м) скважин на базе не более 40–50 м.
При детальных исследованиях требования к методике полевых наблюдений повышаются и сводятся к следующему.
1) плотность профилей должна быть не менее 3 пог. км на 1 км2, причем при детализации, например, грабенообразных прогибов большую часть профилей следует ориентировать вкрест прогиба с расстоянием между ними не более 500 м;
2) в целях повышения пространственной разрешенности расстояние между каналами не должно превышать 25–30 м;
3) группирование сейсмоприемников увеличивается до 48–60 элементов на канал, причем эти элементы располагаются по площади в виде 4–5 параллельных ниток; база группы должна быть не более 50 м.
§ 3.1.2. Методика цифровой обработки
Независимо от содержания решаемой геологической задачи методика обработки должна предусматривать получение временных разрезов с сохранением истинных амплитуд, с высокой разрешенностью отражений, с высоким соотношением сигнал/помеха, а также обеспечивать возможность высокоточного определения интервальных скоростей.
Выполнение указанных требований достигается при использовании усложненного графа обработки, содержащего следующие процедуры:
1) демультиплексация цифровых записей (DMXT);
2) редакция (REDX);
3) коррекция амплитуд за геометрическое расхождение и поглощение (RAMP);
4) вычитание среднескоростных волн-помех (RECON);
5) минимально-фазовая деконволюция исходных записей (DECVTX);
6) широкополосная фильтрация исходных записей (FILVTX);
7) коррекция амплитуд за неидентичность условий возбуждения и приема (NORM);
8) коррекция статических поправок (SUMLAK);
9) коррекция кинематических поправок (сканирование или вертикальные спектры, KINVC);
10) автоматическая коррекция статических поправок (PAKS);
11) накапливание по ОГТ (SUMLC);
12) погоризонтный анализ скоростей (горизонтальные спектры скоростей, HORSP);
13) независимая потрассовая коррекция остаточных фазовых сдвигов в нескольких временных окнах (WINCOR);
14) когерентная фильтрация (AMCOD);
15) нуль-фазовая деконволюция по разрезу (ZEDEC);
16) широкополосная фильтрация по разрезу (FILVTX);
17) когерентная фильтрация (AMCOD);
18) миграция (MIGFK);
19) псевдоакустический каротаж (РАК).
Раздел 3.2. Выбор способа решения
прямой
динамической задачи
При использовании математического моделирования для целей интерпретации сейсмических данных возникает вопрос о выборе способа вычисления теоретического волнового поля. В последнее время для двумерного моделирования получили распространение способы, основанные на лучевом приближении, и более точные способы, базирующиеся на решении дифракционного уравнения Кирхгофа или волнового уравнения в конечных разностях. Выбор способа является, прежде всего, вопросом методическим. Однако нельзя забывать и о стоимостной стороне дела, поскольку затраты машинного времени при вычислениях по точным способам, например по алгоритму Трорея – Хилтермана, для некоторых, даже не очень сложных моделей, могут быть на один-два порядка выше, чем при вычислениях в лучевом приближении. Особенно остро вопрос о выборе способа вычислений стоит при использовании моделирования в итеративном режиме, когда предполагается многократное вычисление СВР.
При выборе способа его вычисления естественно исходить из того класса сейсмологических моделей, который предопределен решаемой при интерпретации геологической задачей. Зафиксировав этот класс моделей, нужно соотнести его с наиболее существенными допущениями, на которых построены конкретные вычислительные алгоритмы. Отправными здесь являются следующие соображения. Теория распространения сейсмических волн на основе лучевых представлений геометрической сейсмики предполагает, прежде всего, абсолютную локальность сейсмических лучей, что равносильно утверждению о бесконечно малой длине волны, а также распространение энергии волны по лучу и зеркальное ее отражение в единственной точке. Согласно волновым представлениям, полная энергия сейсмической волны есть результат суммирования элементарных волн, при этом в одну и ту же точку приема приходит энергия, отраженная от некоторого участка границы, которая, таким образом, должна иметь определенную протяженность. Вследствие этого возникают явления дифракции, благодаря которым у окончаний границ не наблюдается резкого обрыва отраженных волн. При падении плоской волны на границу, содержащую резкие перегибы, их экстремальные точки являются источниками дифрагированных волн. Эти и некоторые другие явления не могут быть рассчитаны в лучевом приближении.
Для оценки величины области формирования отраженного импульса обычно используется параметр первой зоны Френеля F, который рассчитывается по известной формуле:
![]() ,
,
где Н – глубина залегания отражающей границы; l – длина волны. Если протяженность отражающего элемента, связанного с какой-либо неоднородностью в геологическом разрезе, составляет величину F зоны Френеля и более, то этот элемент отобразится на временном разрезе с максимальной амплитудой, соответствующей отражению от бесконечно длинной границы. При уменьшении горизонтальных размеров элемента (меньше F) он будет отображаться на временном разрезе с заметным уменьшением амплитуды, все меньше походить на отражение и все больше приобретать вид дифракции, соответствующей отражающей точке.
В связи с этим для практики моделирования большое значение имеет определение хотя бы примерного набора структурных и стратиграфических моделей, для которых ограничения лучевой теории могут оказаться неприемлемо жесткими и для построения СВР потребуются способы, основанные на волновой теории. Далее рассмотрим примеры таких моделей, причем выбранные модели соответствуют геологическим объектам, нередко обнаруживаемым в Волго-Уральской нефтегазоносной провинции. Для каждой модели вычислялись СВР по двум программам: по программе, алгоритм которой основан на лучевых представлениях, и по программе, реализующей численное решение дифракционного уравнения Кирхгофа.
В первой программе СВР вычисляется путем поиска траекторий нормальных лучей для заданных пунктов взрыва-приема (ПВП) и определения амплитуд отраженных волн. В основу алгоритма второй программы положена простая теория дифракции А. Трорея, которую модифицировал Ф. Хилтерман для случая многослойной среды.
§ 3.2.1. Пример 1. Моделирование микрограбенов
Данный пример (рис. 5) иллюстрирует отличие волновых полей от грабенообразных прогибов при различной их ширине. Последняя варьировалась, исходя из величины зоны Френеля, которая для модели на рис. 5, а при видимой длине волны l = 160 м и глубине границы Н = 2400 м составляет F = 880 м. Поэтому ширина грабенов была задана следующей: l1 = 0,5F = 440 м, l2 = F = 880 м, l3 = 2F = 1760 м.
На временных разрезах, полученных в лучевом приближении (рис 5, б), можно видеть адекватное отображение всех элементов модели грабенообразного прогиба независимо от его ширины. На временных разрезах, полученных по алгоритму Трорея – Хилтермана, наблюдается отчетливая зависимость волновой картины от ширины грабена: при ширине грабена меньше зоны Френеля происходит перекрытие разрыва в отражающих границах за счет дифракции, и при l1 = 0,5F разрыв практически незаметен. Существование его можно обнаружить лишь по небольшой аномалии времени и по некоторому ослаблению амплитуд. Это надо учитывать при практической интерпретации временных разрезов, чтобы избежать неправильных выводов относительно ширины прогиба, пределов распространения вверх по разрезу разрывных нарушений и самого существования прогиба.
§ 3.2.2. Пример 2. Моделирование подрифовых горизонтов
Данный пример (рис. 6) иллюстрирует различие в отображении на временных разрезах плоских горизонтальных границ, расположенных глубже рифогенных образований. На рис. 6, а представлена обобщенная модель рифогенного образования фамен-турнейского возраста, составленная на основе анализа и обобщения сейсмогеологических материалов по большому количеству структур Самарской и Оренбургской областей, рифогенная природа которых доказана. На модели граница 8 соответствует кровле терригенных отложений девона, границы 4 и 5 – бобриковскому горизонту, границы 2 и 3 – верейскому горизонту, граница 1 – кровле жестких отложений. В рифогенных образованиях, расположенных между границами 5 и 8, скорость 6000 м/с, во вмещающих породах – 5400 и 5500 м/с.
Из сравнения временных разрезов на рис. 6, б, в, прежде всего, видно появление на обоих разрезах ложных антиклинальных перегибов по горизонту 8 с амплитудой 20 мс, хотя на модели граница 8 была задана плоской и горизонтальной. Отличие заключается в том, что на временном разрезе, вычисленном с учетом дифракции (рис. 6, в), по горизонту 8 наблюдается резкое уменьшение интенсивности записи на участках флексурообразного перехода от горизонтальной части к ложной антиклинали. Кроме того, флексурообразные перегибы явились источниками ложных (мнимых) дифрагированных волн. Данный пример должен предостеречь от ошибочной интерпретации реальных временных разрезов, на которых встречены аномалии, подобные приведенным на рис. 6, б по горизонту 8. Очевидно, такие аномалии можно принять за горстовидные структуры.
|
Лекция 5 |
Рассмотренные модели являются достаточно "трудными" для расчетов по лучевому методу, но следует учитывать, что соответствующие этим моделям реальные геологические объекты в Волго-Уральской провинции составляют не более 10-20 % от общего числа нефтегазоперспективных объектов. Кроме того, сравнение результатов моделирования для ряда других, менее сложных моделей (антиклинальные складки и флексурообразные перегибы слоев, тонкослоистая пачка с нерезким изменением толщин слоев или с плавно выклинивающимся одним слоем, выступы кристаллического фундамента с выклиниванием слоев в примыкающих отложениях, верейские и довизейские врезы с нерезкой морфологией и др.) показывает, что временные разрезы, рассчитанные в лучевом приближении и по волновой теории, практически идентичны. В связи с этим применение лучевого метода при модельных расчетах с целью интерпретации может быть достаточно широким и полезным. Однако если в моделях имеются такие элементы, как тектонические нарушения, неоднородности с горизонтальными размерами, меньшими зоны Френеля, резкие перегибы слоев с радиусом кривизны, меньшим длины волны, и если при интерпретации используются в количественной форме динамические характеристики записи (например, при решении задач ПГР), то следует пользоваться более точными методами.
Раздел 3.3. Выбор исходного сейсмического импульса
Результатом решения прямой динамической задачи обычно является СВР в виде импульсных сейсмотрасс, которые затем подвергаются свертке с импульсом, моделирующим сейсмический сигнал. Успех использования СВР для целей интерпретации во многом определяется правильным выбором начального приближения этого импульса.
В связи с этим в практике моделирования применяется следующая методика выбора сейсмического импульса. Основой этой методики является аналитическое выражение импульса Пузырева:
![]() , (3.1)
, (3.1)
где a0 – начальная амплитуда (обычно a0 = 1); w0 = 2pf0 – преобладающая частота, Гц; р – затухание; j – начальная фаза.
Определение начального приближения параметров этого импульса (w0, p, j) производится следующим образом. Начальная фаза j принимается равной p/2 (симметричный импульс) на основании того, что в процессе обработки реальных сейсмических записей в результате применения всех видов фильтраций (деконволюция, полосовая фильтрация) стремятся на выходе получить элементарный сигнал симметричной формы (нуль-фазовый).
Преобладающая частота f0 находится по спектру мощности реальных записей, для чего в
заданном фрагменте временного разреза по всем трассам вычисляются
нормированные автокорреляционные функции, которые затем осредняются, в
результате чего получается одна функция ![]() . Для этой функции, предварительно сглаженной, вычисляется
спектр мощности. Квадратный корень из этого спектра принимается за осредненный
амплитудный спектр сейсмического импульса. Этот спектр нормируется, и по нему
находятся два параметра: преобладающая частота f0 и ширина спектра Df на уровне 0,7.
. Для этой функции, предварительно сглаженной, вычисляется
спектр мощности. Квадратный корень из этого спектра принимается за осредненный
амплитудный спектр сейсмического импульса. Этот спектр нормируется, и по нему
находятся два параметра: преобладающая частота f0 и ширина спектра Df на уровне 0,7.
Для определения параметра затухания р используется аналитическое выражение для нормированного амплитудного спектра импульса (3.1) в виде:
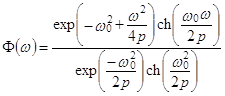 . (3.2).
. (3.2).
Вначале по этой формуле при известном w0 = 2pf0 и p = 5000 вычисляется амплитудный спектр теоретического импульса (3.1), по которому также на уровне 0,7 оценивается ширина спектра Df(1) (первая итерация). Это значение Df(1) сравнивается с определенным по спектру реальных сейсмозаписей значением Df, и если Df(1) > Df, то первоначальное р уменьшается, и наоборот. С новым значением р опять вычисляется по формуле (3.2) спектр F(w), по которому находится новое значение Df(2) (вторая итерация) и т. д. Шаг изменения по р вначале принимается равным 1000, а после получения "вилки" он уменьшается до тех пор, пока не будет выполнено условие |Df(i) – Df| £ 2 Гц, тогда значение р фиксируется.
Полученные оценки w0 и p, а также принятое значение j = p/2 используются для расчета по формуле (3.1) весовых коэффициентов фильтра для свертки с синтетическим временным разрезом в импульсном представлении.
Рассмотренная, методика предназначена для определения начального приближения параметров импульса, которое, как правило, является достаточно хорошим для параметров w0 и p, но принимаемая априори величина j = p/2 может быть весьма приближенной, поскольку на реальном временном разрезе сигнал может отличаться от нуль-фазового. Поэтому в дальнейшем в процессе итеративной коррекции параметров модели все три параметра импульса также корректируются.
Раздел 3.4. Сопоставление
синтетического и
реального временных разрезов
В соответствии с общими принципами анализа двумерных изображений сопоставляемые объекты должны быть разбиты на элементарные единицы, называемые сегментами. В нашем случае (при сравнении РВР и СВР) это понятие обозначает наименьшие элементы (DX, Dt), которые сохраняют физико-геологический смысл. Конкретно: сегменты, выделяемые на сопоставляемых временных разрезах, ограничиваются по оси t интервалом с одним или двумя опорными отражениями или таким интервалом между опорными отражениями, который может представлять самостоятельный интерес для моделирования, по оси Х – участком, который характеризуется примерно одинаковым характером записи и в определенной степени соответствует понятию сейсмофации, принятому в сейсмостратиграфии. Необходимо также отметить, что процедура сегментации, являясь неформальной в принципе, выполняется интерпретатором, а те соображения, которыми он руководствуется при выделении сегментов, создают для каждого из них свой контекст при сопоставлении реального и синтетического разрезов.
Наиболее естественной и наглядной являлась бы оценка, характеризующая в целом сходство соответствующих друг другу (т. е. имеющих один и тот же физико-геологический смысл) сегментов реального и синтетического разрезов. Однако для упрощения будем сопоставлять только участки трасс, входящих в указанные сегменты. Это позволяет свести двумерную (по Х и t) задачу оценки сходства к совокупности одномерных (только по t) задач. По существу предполагается при этом, что волновое поле квазистационарно по X-координате.
Переходя непосредственно к численному оцениванию сходства трасс РВР и СВР, прежде всего, выделим две группы таких оценок:
1) интегральные оценки, характеризующие общий вид сравниваемых объектов;
2) дифференциальные, характеризующие отдельные их элементы.
При оценивании сходства по интегральным критериям основной операцией является интегрирование с использованием полной информации об объектах, а по дифференциальным критериям – дифференцирование, которое применяется как к объектам в целом, так и к их частям. Конкретные виды критериев сходства трасс СВР и РВР рассматриваются ниже.
Отметим лишь одно, важное в методическом аспекте обстоятельство. Достаточно высокий уровень глобальных оценок сходства, построенных по интегральным и дифференциальным критериям, играет роль соответственно необходимого и достаточного условия достижения цели интерпретации. Это значит, что в процессе интерпретации при оценивании сходства с необходимостью нужно переходить от интегральных критериев к дифференциальным. Фактически это соответствует наращиванию степени детальности рассмотрения сравниваемых разрезов.
Так, при решении стратиграфических задач, вызывающих повышенный интерес в связи с проблемой прогнозирования геологического разреза, очевидно, нельзя заканчивать процесс интерпретации по достижению высокой степени сходства по интегральным критериям, поскольку геологическая сущность таких задач часто выражается в столь незначительных вариациях сейсмогеологической модели и соответствующего ей СВР, чувствительностью к которым обладают лишь дифференциальные критерии. Подобного рода чувствительность достигается усложнением процедуры оценивания сходства или построением этой процедуры на итеративно-диалоговых принципах, чем обеспечивается соответствие оценки сходства визуальным и геолого-геофизическим представлениям интерпретатора.
Из рис. 7, а видно, что применение интегральных критериев требует осторожности, поскольку здесь при очевидном отсутствии визуального сходства значение интегральной оценки довольно высоко (0,84). Рис. 7, б и в демонстрируют слабую чувствительность интегрального критерия к малоамплитудным (локальным) особенностям записи: если учесть форму последнего полупериода записи, трассы на рис. 7, 6 визуально более похожи между собой, чем трассы на рис. 7, в. Однако значения сходства по НФВК противоречат этому суждению. Рис. 7, г, д и е иллюстрируют тот факт, что числовые значения интегральных и дифференциальных оценок могут отличаться весьма существенно. Кроме принципиальной разницы в подходах к оцениванию сходства, это объясняется еще и тем, что при вычислении дифференциальных оценок учитывается качественная информация от геофизика-интерпретатора. Так, выполнив стратиграфическую привязку отражений, он может выделить отражения, являющиеся целевыми в решаемой им геологической задаче, и задать их как наиболее важные при оценивании сходства.
Главной методической целью получения оценок сходства является выделение на каждом шаге итеративного процесса интерпретации тех трасс СВР и РВР, сходство между которыми ниже принятого на данном шаге порога. Наличие протяженных участков СВР, характеризующихся пониженными значениями оценок сходства, указывает на необходимость коррекции соответствующего фрагмента сейсмогеологической модели (иногда вплоть до перехода к другой гипотезе о строении геологического разреза).
Раздел 3.5. Целенаправленная
коррекция параметров
тонкослоистых моделей
Как и ранее, будем ориентироваться на класс комбинированных моделей геологических сред, введенный в гл. 2. Напомним, что такие модели состоят из собственно моделируемого интервала, представленного совокупностью тонких слоев, и толстослоистой покрывающей части. В число корректируемых параметров включаются скорости, плотности и мощности тонких слоев, а также параметры импульса, моделирующего сейсмический сигнал.
Из методических соображений разделим процесс оптимизации целевой функции, связывающей оценки сходства с параметрами сейсмомоделирования, на два этапа:
1) предварительная коррекция, выполняемая в диалоговом режиме, когда в процессе коррекции предполагается постоянное и непосредственное участие геофизика-интерпретатора;
2) уточнение параметров моделей в автоматическом режиме путем оптимизации некоторого функционала, описывающего сходство трасс реального и синтетического временных разрезов.
§ 3.5.1. Предварительная коррекция
На этапе предварительной коррекции осуществляется сравнительно грубый подбор параметров модели в диалоговом режиме. Наличие данного этапа позволяет не вводить каких-либо ограничений на величину отклонения параметров модели нулевого приближения от искомого решения. Но вместе с тем если при первой оценке сходства (визуальной или по НФВК) синтетического и реального временных разрезов обнаруживается явное их несходство, то ставится вопрос об изменении модели в целом или о переходе к другой гипотезе о геологическом строении разреза.
Методической основой предварительной коррекции являются следующие положения:
1) при коррекции используются данные о сравнительной чувствительности динамических характеристик записи к изменению параметров тонкослоистой модели, полученные с помощью метода статистических испытаний;
2) в целях ограничения области поиска глобального экстремума из первого этапа исключается и переносится на второй этап коррекция двух параметров исходного импульса (р, j) и в некоторых случаях коррекция толщин слоев;
3) для коррекции систематического отклонения толщин или скоростей в слоях, выражающегося в растяжении или сжатии трасс синтетического разреза, применяются формулы, которые учитывают значения первоначальной скорости и толщины слоя;
4) на каждом шаге коррекции используются результаты сравнения СВР и РВР по НФВК, которые в конце предварительной коррекции могут дополняться сравнением по частным критериям (графики амплитуд и энергий, частотные спектры и др.) или с помощью дифференциальной оценки сходства.
Рассмотрим подробнее перечисленные положения.
|
Лекция 6 |
Чувствительность динамических характеристик к изменению параметров модели
Для обеспечения целенаправленности и сходимости процесса коррекции желательно, чтобы интерпретатор, принимающий решения об изменении параметров модели, руководствовался набором некоторых методических положений.
В результате обработки и анализа относительных отклонений динамических характеристик отмечены следующие закономерности.
1. Из трех динамических характеристик сейсмической записи (Е, F0 и DF) наиболее чувствительной к изменению параметров модели является энергия Е (например, при знакопеременном изменении плотности на 20% относительное изменение энергии в среднем в 8 раз выше, чем изменение ширины амплитудного спектра на уровне 0,7, и в 12 раз выше, чем изменение максимума частотного спектра F0.
2. Наиболее инертной (малочувствительной к изменению параметров модели) является преобладающая частота записи F0, например, при знакопеременном изменении плотностей, скоростей и мощностей слоев на 20% F0 изменяется в среднем на 4% при знакопеременном изменении толщин даже на 40% преобладающая частота F0 изменяется на 5%. Этот результат означает, что при интерпретации с помощью итеративного моделирования частота f0 должна уточняться на начальных шагах итеративного процесса коррекции.
3. Если изменение плотностей на одинаковую относительную величину во всех слоях и с одним знаком не изменяет самой СС и ее динамических характеристик, то аналогичное изменение скоростей, например на 20%, вызывает изменение Е в среднем на 30%, DF на 14% и F0 на 11%. В данном случае при сравнительно невысоких средних отклонениях характеристик DF и F0 наблюдается значительно большая их дисперсия по сравнению с дисперсией этих характеристик при другом характере изменения скорости или при изменении других параметров модели. Полученный результат интересен в тех случаях, когда известно, что пластовые скорости содержат систематические погрешности: их, очевидно, нужно устранять возможно раньше, на начальных шагах процесса коррекции.
4. Знакопеременное изменение плотностей, например на 20%, приводит к изменению энергии в среднем на 80%, DF на 17% и F0 на 10%. Аналогичное изменение скоростей, однако, не приводит к заметно большему изменению указанных характеристик, хотя в этом случае изменяются не только коэффициенты отражения, но и времена вступления волн.
5. Знакопеременное изменение толщин слоев приводит к очень слабому изменению динамических характеристик записи. Например, при изменении толщин на 20% энергия Е изменяется в среднем на 12%, DF на 7,5% и F0 на 3,5%. Необходимо подчеркнуть важность данного результата, поскольку согласно ему в процессе коррекции модели даже при значительном изменении положения промежуточных границ в тонкослоистой пачке (даже до 40-50% от толщины слоя) без существенного изменения общей ее мощности не следует ожидать заметного изменения динамических характеристик записи. Отсюда можно сделать вывод: коррекцию толщин слоев целесообразно оставлять на второй этап.
6. Изменение частоты исходного сигнала f0 на ±20% приводит к существенному изменению динамических характеристик: энергия Е изменяется в среднем на 38%, DF на 18% и F0 на 26%, причем наблюдается значительная дисперсия этих отклонений. Данный результат подкрепляет сделанный ранее вывод о том, что коррекция преобладающей частоты f0 исходного импульса должна выполняться на первых шагах итеративного процесса коррекции.
Приведенные оценки относительных изменений динамических характеристик записи касаются в основном тех случаев, когда параметры модели изменялись на 20 и 40%; естественно, изменения параметров модели на 15, 10% и менее вызывают меньшие изменения характеристик записи, но линейной зависимости здесь нет.
Что касается преобладающей частоты импульса f0, то ее коррекцию необходимо осуществлять на первых шагах итеративного процесса коррекции, поскольку преобладающая частота записи F0 гораздо сильнее зависит от f0, чем от изменений пластовых параметров тонкослоистой пачки.
Коррекцию толщин слоев целесообразно также переносить на этап автоматической коррекции в двух случаях. Во-первых, когда на синтетическом временном разрезе уже получены временные соотношения (интервалы между соседними отражениями или экстремумами), которые близки к временным соотношениям на реальном разрезе. Во-вторых, если коррекция модели начинается с участка, расположенного в непосредственной близости к глубокой скважине, то толщины слоев принимаются достоверно известными и, естественно, их грубая коррекция не требуется.
§ 3.5.2. Уточнение параметров модели в автоматическом режиме
Если исходная геологическая гипотеза верна, то геофизик-интерпретатор на первых шагах коррекции сравнительно быстро находит правильные решения и сходство СВР и РВР улучшается достаточно быстро. Затем после 10–15 итераций, когда для дальнейшего улучшения сходства разрезов требуется вводить в модель все более тонкие детали, то процесс сильно замедляется. С этого момента начинает играть значительную роль фактор времени, для преодоления которого любые средства автоматизации становятся малоэффективными.
Ниже излагается подход к постановке задачи и выбору численного метода ее решения, который ориентирован на отыскание глобального экстремума целевой функции, связывающей потрассную оценку сходства с параметрами сейсмомоделирования, причем размерность и положение области поиска при реализации данного подхода могут итеративно меняться в зависимости от достигнутого к настоящему моменту результата и суждения геофизика, ведущего процесс интерпретации.
Введем два допущения, упрощающих процесс образования сейсмического волнового поля и необходимых для построения целевой функции.
Первое допущение состоит в том, что волновое поле на временных разрезах аппроксимируется моделью, в которой возбуждение среды производится плоскими волнами, падающими по нормали к границе раздела, и практически отсутствуют многократные отражения. В этом случае можно учитывать единственный динамический фактор – коэффициент отражения.
Второе допущение состоит в том, что сейсмический сигнал аппроксимируется теоретическим импульсом Пузырева (3.1).
Глава 4. Программно-алгоритмическое обеспечениеРаздел 4.1. Решение прямой динамической задачи в лучевом приближении
§ 4.1.1. Поиск траектории нормального луча
Полный и точный учет амплитудного фактора фокусировки сейсмической энергии возможен при сопоставлении элементу отражающей границы пунктов взрыва-приема (ПВП), которые могут иметь нормальное отражение от этого элемента. Величина указанного элемента должна быть такой, чтобы часть среды, ограниченная нормалями от его концов, удовлетворяла определению лучевой трубки. Всю совокупность траекторий нормальных лучей, необходимую для построения временного разреза, можно получить, рассмотрев все элементы всех отражающих границ модели среды.
Алгоритм нахождения траекторий нормальных лучей применяется в ходе просмотра с заданным шагом DX всех отражающих границ заданной модели. Если величина шага достаточно мала, ПВП, которые могут иметь нормальные отражения от рассматриваемого элементарного участка отражающей границы, располагаются между точками выхода нормалей, трассированных из его концевых точек. Для каждого полученного таким образом ПВП ведется поиск такого нормального луча, точка выхода которого с заданной точностью совпадает с X-координатой этого ПВП. Итеративный алгоритм трассирования нормальных лучей из внутренних точек указанного элементарного участка позволяет завершить поиск, затратив минимальное количество трассированных лучей, что важно с точки зрения быстродействия программы.
Обозначим через ![]() и
и ![]() абсциссы точек,
ограничивающих (соответственно слева и справа) рассматриваемый элемент
отражающей границы на n-м шаге итерационного процесса, через
абсциссы точек,
ограничивающих (соответственно слева и справа) рассматриваемый элемент
отражающей границы на n-м шаге итерационного процесса, через ![]() и
и ![]() абсциссы точек выхода на
поверхность нормалей к отражающей границе в точках с абсциссами
абсциссы точек выхода на
поверхность нормалей к отражающей границе в точках с абсциссами ![]() и
и ![]() соответственно, а через XN
– абсциссу ПВП (рис. 9, а).
соответственно, а через XN
– абсциссу ПВП (рис. 9, а).
Сначала из точек ![]() и
и ![]() отражающей
границы восстанавливаются нормали, для двух полученных точек выхода с абсциссами
отражающей
границы восстанавливаются нормали, для двух полученных точек выхода с абсциссами
![]() и
и ![]() проверяется условие
проверяется условие ![]() и таким образом
определяются количество и номера ПВП, находящихся между точками выхода нормалей.
Именно здесь элементу отражающей границы ставится в соответствие ПВП, которые
могут иметь нормальное отражение от него. Если данному условию не удовлетворяет
ни один ПВП, делается следующий шаг по отражающей границе. Для каждого ПВП из
интервала
и таким образом
определяются количество и номера ПВП, находящихся между точками выхода нормалей.
Именно здесь элементу отражающей границы ставится в соответствие ПВП, которые
могут иметь нормальное отражение от него. Если данному условию не удовлетворяет
ни один ПВП, делается следующий шаг по отражающей границе. Для каждого ПВП из
интервала ![]() проверяется условие
проверяется условие
![]() , (4.1)
, (4.1)
где e – заданная малая
величина. Выполнение (4.1) означает конец итерационного процесса, а его
результаты определяются траекторией, соответствующей ![]() , если
, если ![]() , или
, или ![]() при
при ![]() .
.
В случае, когда таким путем траектория не найдена, а элемент отражающей границы не меньше заданной величины, из точки отражающей границы с абсциссой
![]()
восстанавливается нормаль к отражающей
границе. Если абсцисса ![]() ее точки выхода
достаточно близка к ПВП, т. е.
ее точки выхода
достаточно близка к ПВП, т. е. ![]() ,
считается, что искомая траектория определена. В противном случае проверяется
условие принадлежности
,
считается, что искомая траектория определена. В противном случае проверяется
условие принадлежности ![]() интервалу
интервалу
![]() . Если это условие выполнено, происходит переход к следующей
итерации:
. Если это условие выполнено, происходит переход к следующей
итерации:
![]()
![]()
Невыполнение этого условия
означает, что рассматриваемый элемент модели не является лучевой трубкой, и
если он не слишком мал, то отрезок отражающей границы между точками с
абсциссами ![]() и
и ![]() делится пополам, после
чего процесс поиска начинается как бы сначала (n =
0).
делится пополам, после
чего процесс поиска начинается как бы сначала (n =
0).
По исчерпанию всех ПВП, найденных
в интервале ![]() , делается следующий шаг по
отражающей границе.
, делается следующий шаг по
отражающей границе.
|
Лекция 7 |
§ 4.1.2. Учет динамических факторов
Амплитуды отражений рассчитываются на основе следующих положений теории распространения волн:
1) непрерывность напряжений и смещений для плоских волн, отражающихся от плоских границ;
2) сохранение энергии внутри лучевой трубки;
3) постоянный параметр поглощения Q, учитывающий минимально-фазовый механизм потерь при распространении за счет поглощения энергии.
Условия непрерывности на границе дают для коэффициента отражения простейшую формулу, строго справедливую в рассматриваемом случае нормального падения луча:
![]() ,
,
где ![]() – акустические жесткости слоев, лежащих соответственно выше
и ниже отражающей границы.
– акустические жесткости слоев, лежащих соответственно выше
и ниже отражающей границы.
Для учета геометрического расхождения воспользуемся известной формулой:
![]() ,
,
где L – коэффициент геометрического расхождения; Dl – поперечный размер сечения лучевой трубки плоскостью падения волны в точке наблюдения; Dq – интервал углов выхода, ограничивающий лучевую трубку. Обозначив R амплитудный фактор расхождения, с учетом соотношения R = L-2
R=![]() , (4.2)
, (4.2)
здесь Dq и DX – приращения угла засылки лучей и точек их выхода соответственно; aN – угол выхода нормального луча.
На основе формулы (4.2) построен итеративный алгоритм вычисления амплитудного фактора R, учитывающего геометрическое расхождение. Упрощенное описание его сводится к следующему.
Шаг 1. Засылка из данного пункта взрыва-приема пяти лучей с углами qN-F, qN‑F/2, qN, qN+F/2 и qN+F и получение соответствующих точек выхода (F – малая величина порядка ~ 10-4 – 10-5, задаваемая в исходных данных).
Шаг 2. Формирование из пяти трассированных на шаге 1 лучей системы из двух пар лучей так, чтобы каждая пара вмещала бы данный ПВП и чтобы одна из пар вмещала другую (см. рис. 9, б); вычисление двух значений амплитудного фактора R:
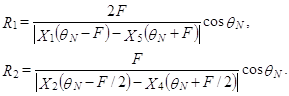
Шаг 3. Проверка предельного перехода
![]() .
.
Если "да", то R=R2 и алгоритм заканчивается. Если "нет", проверяется условие |X1‑X5| < 50. При невыполнении этого условия расхождение считается вычисленным условно. В случае выполнения приращение увеличивается в 2 раза. Переход к шагу 1. При этом делается не более 16 попыток достигнуть сходимости в формуле (4.2) за счет увеличения F.
С учетом вышерассмотренных динамических факторов вычисляется импульсный временной разрез, в котором до свертки с заданным сейсмическим сигналом можно также произвести учет частотно-зависимого поглощения сейсмической энергии.
Влияние фокусировки сейсмической энергии на амплитуду отраженных сигналов учитывается автоматически в ходе вычисления траекторий нормальных лучей. Явления фокусировки возникают при наличии локальных отрицательных перегибов в поведении границ (вогнутостей), когда нормальные лучи пересекаются (образуют каустики) в непосредственной близости от линии наблюдения. Примером могут служить участки перехода от горизонтальной границы к крылу пологой структуры. В этом случае для одного и того же ПВП находятся два и более нормальных лучей с почти равными временами прихода отраженных сигналов которые автоматически суммируются.
Раздел 4.2. Расчет временных разрезов на основе дифракционной теории трорея
При разработке упрощенной теории сейсмической дифракции А. Трореем за основу был взят дифракционный интеграл Гельмгольца, который выражает значение упругого потенциала jp (или преобразования Лапласа от потенциала jp) поля отраженных волн в произвольной точке р, расположенной внутри замкнутой поверхности S, через заданный на этой поверхности потенциал jS :
![]() , (4.3)
, (4.3)
где jр – преобразование Лапласа от скалярного потенциала поля отраженных волн в точке р внутри замкнутой поверхности S; r – расстояние от р до элемента DS на S; п – внешняя нормаль к S; V – скорость; р – трансформанта Лапласа; jS – заданный на S потенциал.
Данное уравнение имеет место лишь в рамках акустического приближения, поэтому его решение содержит только продольные волны.
Трансформируя поверхность S в полусферу с бесконечным радиусом, на диаметральной плоскости которой расположен отражающий элемент, и аппроксимируя отражающую поверхность набором плоских полос бесконечной длины и шириной Dx=x2 – x1 (рис. 10, а), А. Трорей получил решение дифракционного интеграла (4.3) для одной[1] такой полосы в виде
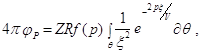 (4.4)
(4.4)
здесь R – коэффициент отражения; f(р) – преобразование Лапласа от импульса волны в источнике Q; смысл обозначений Z, q и x ясен из рис. 10. a. Для интегрирования выражения (4.4) следует выразить x через угол q (рис. 10, a), однако два важных вывода можно сделать и до этого
1. На каждом краю отражающего (дифрагирующего) элемента (в точках А рис. 10, б) фаза дифракции изменяется на 180°. В самом деле, пусть D1 и D2 – результаты интегрирования (4.4) в направлении линии АВ (рис. 10, а) на расстоянии Х1 и Х2 соответственно (в пределах от -p/2 до p/2). Тогда jр=D2-D1. Если Х1<0, что соответствует положению точки p над полосой, то jр=V–D2–D1 (здесь V обозначен член, соответствующий отражению). Отсюда следует, что D2 меняет знак при переходе Р через край полосы.
2. На дифрагирующем краю форма отраженной и форма дифрагированной волн совпадают, но величина амплитуды дифрагированной волны в 2 раза меньше. Действительно, пусть точка Р при движении слева направо пересекает дифрагирующую полосу (рис. 10, б). Для распространения алгоритма Трорея на случай многослойной среды с криволинейными Распределение амплитуд показано на этом же рисунке. Из условий непрерывности jр при переходе через край А имеем D2=V–D2, т.е. D2=V/2, что и требовалось.
3. Границами
раздела, с горизонтальным градиентом пластовых скоростей и плотностей, с
угловыми несогласиями и выклиниваниями Ф. Хилтерман предложил вычислительный
способ приведения среды над каждой границей поочередно к однослойной с единой постоянной
скоростью. Для этой цели из каждого пункта наблюдения с равным шагом по углу
производится трассирование лучей в исходной модели, после чего каждый прослеженный
луч заменяется прямолинейным лучом, выходящим из пункта наблюдения под тем же
углом (рис. 10, в). Мнимое положение края плоского элемента рассчитываемой
границы с номером j находится на прямолинейном
луче на расстоянии, равном ![]() где Vi – локальная скорость; ti –
время прохождения трассированного луча в i-м
слое (соответствующий пример представлен на рис. 10, в для границы 3).
Множество всех полученных таким образом мнимых точек образует мнимую
модель, состоящую из одной границы с одной постоянной скоростью. От всех краев
плоских элементов, составляющих эту мнимую границу, дифрагированные волны
правомерно рассчитывать по "простой теории" Трорея.
где Vi – локальная скорость; ti –
время прохождения трассированного луча в i-м
слое (соответствующий пример представлен на рис. 10, в для границы 3).
Множество всех полученных таким образом мнимых точек образует мнимую
модель, состоящую из одной границы с одной постоянной скоростью. От всех краев
плоских элементов, составляющих эту мнимую границу, дифрагированные волны
правомерно рассчитывать по "простой теории" Трорея.
Раздел 4.3. Количественное оценивание сходства трасс синтетического и реального временных разрезов
Как отмечено в разд. 3.4, при реализации технологии интерпретации данных сейсморазведки, основанной на математическом моделировании, используются оценки сходства, имеющие интегральный и дифференциальный характер.
§ 4.3.1. Способы вычисления предварительных оценок
В качестве первоначальной оценки сходства отрезков сейсмических трасс, входящих в соответствующие друг другу сегменты применяется интегральная оценка с помощью широко известной нормированной функции взаимной корреляции вида:
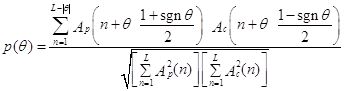 ,
,
где Ар и Ас – отсчеты реальной и синтетической трасс; L – длина сравниваемых трасс; п – номер отсчета сравниваемых трасс; q = –(L–1), –(L–1)+1, …, (L–1) – сдвиг. Из формулы видно, что р(q) Î [-1, 1], причем случай р = ±1 соответствует полному подобию АP(t) и Ас(t) с точностью до полярности, а р=0 – полной их некоррелированности.
Оценка сходства R для заданных трасс и временные сдвиги между ними получаются в результате обработки НФВК р(q) по следующему алгоритму.
1) выделяются все положительные максимумы НФВК;
2) в координатах (р, q)
строится окно поиска [(![]() ),
± КТ
),
± КТ![]() ], где
], где ![]() –
средняя амплитуда всех экстремумов рассматриваемой функции;
–
средняя амплитуда всех экстремумов рассматриваемой функции; ![]() – средний период
(среднее расстояние между экстремумами); КR и КT – задаваемые константы;
– средний период
(среднее расстояние между экстремумами); КR и КT – задаваемые константы;
3) за оценку R принимается наибольший из всех положительных экстремумов НФВК, попадающих в окно поиска;
4) в случае, если указанное окно не содержит ни одного положительного экстремума, считается, что между сравниваемыми трассами сходство полностью отсутствует; аналогично интерпретируется и случай, когда в окне имеются два и более положительных экстремумов с примерно равными амплитудами, которые характеризуют минимальный уровень значимости параметра R.
В качестве простейшей дифференциальной оценки сходства используется разность между численными производными сравниваемых отрезков сейсмических трасс, при этом для большей устойчивости численные производные сглаживаются путем суммирования на малой базе Вz. Конкретно, вычисляется модульная оценка:
![]()
где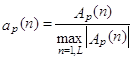 ,
, 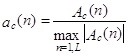 , n1=п – 0,5(Вz–1), n2=п + 0,5(Вz–3) – нормированные амплитудные значения отрезков трасс
РВР и СВР, а также квадратичная оценка Ssq, отличающаяся от
предыдущей тем, что вместо модуля разности сумм в ней используется квадрат
этой разности. Понятно, что нулевые значения этих оценок соответствуют полному
сходству кривых (по используемому критерию); рост значений этих оценок
соответствует нарастанию их несходства.
, n1=п – 0,5(Вz–1), n2=п + 0,5(Вz–3) – нормированные амплитудные значения отрезков трасс
РВР и СВР, а также квадратичная оценка Ssq, отличающаяся от
предыдущей тем, что вместо модуля разности сумм в ней используется квадрат
этой разности. Понятно, что нулевые значения этих оценок соответствуют полному
сходству кривых (по используемому критерию); рост значений этих оценок
соответствует нарастанию их несходства.
§ 4.3.2.
Способ построения дифференциальных оценок, основанный
на анализе характерных точек трасс СВР и РВР
При формировании репрезентативной системы частных критериев сходства используются следующие предположения:
1) в процессе визуального сопоставления трасс СВР и РВР геофизик-интерпретатор выделяет так называемые характерные точки этих кривых – нули и экстремумы;
2) визуальное сопоставление каждой пары трасс основывается на следующих непосредственно воспринимаемых геофизиком-интерпретатором факторах: общее число и порядок следования характерных точек, соотношение амплитуд экстремумов, разница в положении абсцисс характерных точек.
Согласно следующему предположению искомая система частных критериев сходства двух кривых А(1)(t) и А(2)(t), являющихся отрезками трасс РВР и СВР соответственно, включает в себя безразмерные критерии четырех типов:
1)
рассогласование в соотношениях амплитуд
сопоставленных друг другу экстремумов (рис. 11): 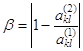 ,
, ![]() , где k и l – порядковые номера этих экстремумов, отсчитанные от начала
рассматриваемого временного интервала; п(k) и п(l) – соответствующие
им номера отсчетов в дискретизированном представлении кривых;
, где k и l – порядковые номера этих экстремумов, отсчитанные от начала
рассматриваемого временного интервала; п(k) и п(l) – соответствующие
им номера отсчетов в дискретизированном представлении кривых;
2)
рассогласование в относительном
положении сопоставленных экстремумов на полупериоде: 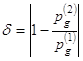 ,
, ![]() . Где g – порядковый номер данного экстремума среди других экстремумов,
зафиксированных в рассматриваемом временном интервале; п(g) –
номер соответствующего ему отсчета; смысл
. Где g – порядковый номер данного экстремума среди других экстремумов,
зафиксированных в рассматриваемом временном интервале; п(g) –
номер соответствующего ему отсчета; смысл ![]() и
и
![]() ясен из рис. 11;
ясен из рис. 11;
3)
рассогласование в ширине полупериода: 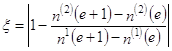 , где e – порядковый номер нуля функций А(t), c которого
начинается данный полупериод, среди других нулей, выделенных в рассматриваемом
интервале, а смысл остальных обозначений ясен из рис. 11;
, где e – порядковый номер нуля функций А(t), c которого
начинается данный полупериод, среди других нулей, выделенных в рассматриваемом
интервале, а смысл остальных обозначений ясен из рис. 11;
4)
рассогласование в положении
сопоставленных экстремумов на оси времени:  ,
здесь Dmax –
заданное максимально допустимое отклонение.
,
здесь Dmax –
заданное максимально допустимое отклонение.
для выявления ловушек сложного экранирования и прямого обнаружения залежей по данным сейсморазведки
Раздел 5.1. Применение сейсмомоделирования при решении стратиграфических задач (изучение детального строения нефтегазоперспективных толщ)
|
Лекция 8 |
Решение этой задачи изучим на примере интерпретации временного разреза по профилю 017801 в Самарской области, проходящему вкрест северо-восточного борта Муханово-Ероховского прогиба от скв. 19 Капитоновская через скв. 28 Винно-Банновская и 11 Мочалеевская. Рассмотрим результаты интерпретации только по участку профиля в пределах Винно-Банновского поднятия (протяженность участка 2,5 км). По глубине был выбран интервал терригенных отложений нижнего карбона, который на сейсмическом временном разрезе заключен между опорными отражающими горизонтами У и Т стратиграфически сопоставляемыми с пластом глин тульского горизонта и кровлей карбонатных отложений турне соответственно.
Двумерная модель нулевого приближения строилась только по данным сейсморазведки, для чего использовались временной разрез, глубинный сейсмический разрез и разрез ПАК. Выбор такого варианта построения был обусловлен тем, что в имеющихся на профиле скважинах не проводился АК и, кроме того, преследовалась цель сопоставить окончательный результат интерпретации с данными бурения. По этой причине модель нулевого приближения, все промежуточные модели и окончательную модель следует рассматривать как эффективные сейсмические модели.
Полученная в результате коррекции параметров окончательная сейсмологическая модель показана на рис. 12, а, сопоставление фрагментов реального и синтетического временных разрезов проведено на рис. 12, б, в соответственно. Количественная оценка сходства этих разрезов с помощью нормированной функции взаимной корреляции дала такие результаты: максимальные значения, например, по трассам 88, 120 и др. достигают 0,97, минимальные значения – не ниже 0,85, в среднем же эта оценка равна 0,921. Такое сходство, несомненно, можно признать достаточно высоким.
В процессе итеративного моделирования корректировались не только параметры тонких слоев модели, но и параметры импульса, моделирующего сейсмический сигнал. В итоге было установлено, что параметры оптимального импульса изменяются по профилю следующим образом: преобладающая частота – от 41 до 49 Гц, затухание – от 9000 до 10300, фаза – от 1,43 до 1,95. С учетом такого изменения параметров исходного импульса рассчитывался окончательный СВР на рис. 12, в.
О точности модели после коррекции можно судить по сопоставлению с данными бурения по скв. 28 Винно-Банновская (рис. 8, д). Детальный скоростной разрез по ней получен путем прогнозирования по данным промысловой геофизики и затем профильтрован нуль-фазовым фильтром 20-100 Гц. Такое сопоставление показывает, что подбор и оптимизация модели выполнены достаточно точно.
При анализе окончательной сейсмогеологической модели на рис. 12, а были получены важные геологические результаты.
Во-первых, во всех пластах моделируемого интервала наблюдается изменение упругих параметров (скорости и плотности) по латерали. Наибольшие изменения отмечаются в нижней части интервала, т.е. в пластах песчаника и глин радаевского и елховского горизонтов. Менее изменчивы параметры пластов тульского горизонта, например скорость в тульской плите изменяется сравнительно плавно и в пределах не более 4%. Существенно большую изменчивость скорости в пластах песчаника и глин нижезалегающих отложений бобриковского, радаевского и елховского горизонтов можно объяснить значительной их неоднородностью, т.е. в пластах песчаника встречаются сильно заглинизированные участки и, наоборот, глины содержат неравномерно распределенный песчаный материал.
Во-вторых, локализация зоны выклинивания пласта С-Ш на северо-восточном крыле Винно-Банновской структуры в значительной мере меняет перспективы выявления здесь структурно-литологической ловушки, связанной с этим пластом. Ранее по результатам исследований, в которых использовались только динамические характеристики записи, линия выклинивания этого пласта намечалась на юго-западном крыле структуры (на 1 км "левее" на рис. 12, а), и было высказано предположение о существовании здесь ловушки структурно-литологического типа. Теперь на основе новых данных, полученных с помощью моделирования, становится очевидным, что выклинивание пласта С-Ш происходит северо-восточнее, т.е. за пределами структуры, и существование ловушки данного типа является маловероятным. Заметим также, что при интерпретации данные ГИС скв. 28 Винно-Банновская не использовались, поскольку по этим данным пласт С-Ш идентифицируется неоднозначно.
В-третьих, к юго-западу от скв, 28 Винно-Банновская, на расстоянии примерно 400–500 м, в пределах почти всей песчано-глинистой толщи нижнего карбона (бобриковский, радаевский и елховский горизонты) отчетливо выделяется зона разуплотнения, отображающаяся на модели понижением скоростей и плотностей, а на трассах временных разрезов в виде локального изменения формы записи (например, появления глубокого минимума перед отражением от кровли турне). В этой зоне разуплотнения можно ожидать улучшенные коллекторские свойства пластов песчаника радаевского и бобриковского горизонтов по сравнению с коллекторскими свойствами в скв. 28 Винно-Банновской.
В-четвертых, обращаясь к распределению скоростей и плотностей в карбонатных отложениях турнея, можно видеть, что имеются участки с заметно пониженным значением этих параметров. Наиболее контрастный из них расположен на пикетах 33,0-39,0 (трассы 89-103), т.е. на юго-западном склоне Винно-Банновского поднятия. На временных разрезах данная аномалия упругих параметров отображается в виде значительного, почти в 2 раза, ослабления амплитуд отражения Т. Понижение скоростей в пределах аномалии составляет не менее 1300 м/с, т.е. скорости уменьшаются от 6300–6500 м/с за пределами аномалии до 5050 м/с в ее центральной части. Наиболее вероятным объяснением природы этой аномалии является увеличение пористости пород турне. Расчеты показывают, что в центральной части аномалии пористость выше на 10–13% по сравнению с пористостью за ее пределами, где она была принята равной 3%. При такой пористости породы турне могут являться хорошим коллектором, и, следовательно, можно предположить существование здесь литологически ограниченной ловушки углеводородов. Размеры этой ловушки по рассматриваемому профилю невелики – не более 0,5–0,6 км, но не исключено, что такая высокопористая зона протягивается по простиранию северо-восточного борта Муханово-Ероховского прогиба на значительное расстояние.
Раздел 5.2. Применение сейсмомоделирования при решении структурных задач (выявление грабенообразных прогибов)
Важным резервом прироста запасов нефти и газа на территории Волго-Уральской нефтегазоносной провинции являются структуры, контролируемые зонами погребенных девонских грабенообразных прогибов. Поэтому в настоящее время общей задачей исследований в этом направлении является оценка возможности выявления масштабов распространения грабенообразных прогибов и связанных с ними месторождений нефти в тех районах Волго-Уральской провинции, где они пока не получили должного практического использования.
Полученные в результате качественной интерпретации временных разрезов модели грабенообразных прогибов являются весьма приближенными, и такие параметры прогибов, как ширина, амплитуда сброса и др. могут иметь существенные отклонения от истинных. Более точные значения этих параметров можно определить путем применения методики интерпретации, основанной на итеративном математическом моделировании. Рассмотрим результаты такой интерпретации на примере временного разреза по профилю 24, пересекающему Санчелеевский грабенообразный прогиб в северной его части. Несмотря на то, что на временном разрезе (рис. 13, в) признаки прогиба в записи отражающего горизонта Д выражены отчетливо, построить достаточно корректную модель, применяя стандартные приемы интерпретации, оказалось невозможным. Поэтому в качестве априорной модели (модели нулевого приближения) были поочередно рассмотрены пять вариантов, различающихся тем, что строение девонских отложений и фундамента видоизменялось от неглубокого синклинального прогиба с амплитудой 50 м и шириной 1,5 км до узкого грабена с амплитудой 200 м и шириной 0,5 км. При моделировании грабена изменялись не только амплитуда и ширина, но и форма краевых частей пластов, примыкающих к линии сброса, и строение опущенного блока. Детальная скоростная характеристика девонских отложений была спрогнозирована на основе данных промысловой геофизики по скважине, расположенной в 3,0 км от профиля. Расчет волнового поля производился по программе 57511 из пакета "Вестерн Джеофизикал Компани", алгоритм которой основан на численном решении дифракционного интеграла Кирхгофа для многослойной среды. Выбор такого способа расчета обусловлен тем, что интерпретируемый временной разрез на рис. 13, в не подвергался миграции.
Процесс подбора модели осуществляется следующим образом. Вначале путем поочередного сравнения синтетических временных разрезов с реальным разрезом производился выбор наиболее правдоподобной модели из пяти заданных. На этом этапе были исключены модели с эрозионными прогибами в кыновских отложениях и фундаменте, а также модели с грабеном, в которых амплитуды разрывных нарушений по всем отложениям (от саргаевских слоев до фундамента) одинаковы. Синтетические временные разрезы по всем этим моделям имели лишь отдаленное сходство с реальным временным разрезом. Для дальнейшего анализа и коррекций была оставлена модель, тип которой показан на рис. 13, а. В этой модели коррекции подверглись главным образом ширина и глубина грабена, а также амплитуда ступени в опущенном блоке. Окончательная модель и соответствующий ей синтетический временной разрез представлены на рис. 13, а, б. Последний имеет сходство с реальным разрезом не только в общих чертах, но и в некоторых деталях. Прежде всего обращает на себя внимание то, что волновой картиной подтверждается частичное "перекрытие" грабена за счет дифракции по отложениям саргаевского и кыновского горизонтов. Кроме того, дифрагированные волны от краевых частей пластов, примыкающих к линии сброса, проявляются достаточно отчетливо, хотя интенсивность их заметно ниже интенсивности отраженных волн от тех же границ. Заметим, что на реальном разрезе предполагаемая дифрагированная волна также значительно слабее соответствующей отраженной. Далее, на синтетическом временном разрезе, так же как и на реальном, отчетливо проявляются горизонтальные участки синфазностей, соответствующие опущенному блоку грабена. В процессе подбора модели немаловажной оказалась и такая деталь: для улучшения сходства временных разрезов пришлось в ряд слоев саргаевского и кыновского горизонтов ввести градиенты скорости, благодаря чему уменьшились коэффициенты отражения границ в области грабена.
Содержание
Лекция 1. 1
Введение. 1
Глава 1. Общие принципы интерпретации данных сейсморазведки на основе математического моделирования. 3
Раздел 1.1. Системный анализ проблемы интерпретации данных сейсмических наблюдений 3
Раздел 1.2. Теоретические вопросы автоматизированной интерпретации данных сейсморазведки 4
Лекция 2. 4
Глава 2. Способы построения сейсмических моделей геологических сред. 6
Раздел 2.1. Построение одномерных моделей. 6
Раздел 2.2. Построение двумерных моделей. 7
§ 2.2.1. Построение модели по данным бурения. 8
Лекция 3. 8
§ 2.2.2. Построение моделей по данным бурения и сейсморазведки. 8
§ 2.2.3. Построение моделей по данным сейсморазведки. 9
§ 2.2.4. Влияние нефтегазонасыщенности на упругие свойства пород. 10
Глава 3. Методика интерпретации на основе итеративного моделирования. 12
Раздел 3.1. Особенности получения и обработки сейсмических данных, интерпретируемых на основе моделирования. 12
Лекция 4. 12
§ 3.1.1. Методика полевых наблюдений. 12
§ 3.1.2. Методика цифровой обработки. 13
Раздел 3.2. Выбор способа решения прямой динамической задачи. 14
§ 3.2.1. Пример 1. Моделирование микрограбенов. 15
§ 3.2.2. Пример 2. Моделирование подрифовых горизонтов. 15
Лекция 5. 16
Раздел 3.3. Выбор исходного сейсмического импульса. 16
Раздел 3.4. Сопоставление синтетического и реального временных разрезов. 17
Раздел 3.5. Целенаправленная коррекция параметров тонкослоистых моделей. 19
§ 3.5.1. Предварительная коррекция. 19
Лекция 6. 20
§ 3.5.2. Уточнение параметров модели в автоматическом режиме. 21
Глава 4. Программно-алгоритмическое обеспечение. 23
Раздел 4.1. Решение прямой динамической задачи в лучевом приближении. 23
§ 4.1.1. Поиск траектории нормального луча. 23
Лекция 7. 24
§ 4.1.2. Учет динамических факторов. 24
Раздел 4.2. Расчет временных разрезов на основе дифракционной теории трорея. 26
Раздел 4.3. Количественное оценивание сходства трасс синтетического и реального временных разрезов 27
§ 4.3.1. Способы вычисления предварительных оценок. 27
§ 4.3.2. Способ построения дифференциальных оценок, основанный на анализе характерных точек трасс СВР и РВР 28
Глава 5. Использование моделирования для выявления ловушек сложного экранирования и прямого обнаружения залежей по данным сейсморазведки. 30
Раздел 5.1. Применение сейсмомоделирования при решении стратиграфических задач (изучение детального строения нефтегазоперспективных толщ) 30
Лекция 8. 30
Раздел 5.2. Применение сейсмомоделирования при решении структурных задач (выявление грабенообразных прогибов) 32
Содержание. 34
[1] Это обстоятельство не снижает общности решения, поскольку граница произвольной формы может быть аппроксимирована последовательностью таких полос.