Реферат: Электроснабжение
Amax <= A[Imax,k]
A[Imax,k] <= A[k,k]
A[Imax,k] <= Amax
for i=k+1 to n do A[i,k] <= A[i,k]/Amax
(*перестановка и исключение по столбцам*)
for j=k+1 to n do
3.8.1. Amax<=A[Imax,j]
A[Imax,j]<=A[k,j]
A[k,j]<=Amax
if Amax<>0 then
for i=k+1 to n do
A[i,j]<=A[i,j]-A[i,k]*Amax
if retcode=0 then (*разложение успешно*)
(*решить СЛУ Ly=b и Vx=y *)
for i=2 to n do

for k=n downto 1 do
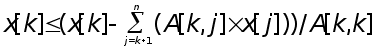
return
end.
АЛГОРИТМ ЯКОБИ
Входные
параметры:
![]() -
вектор начальных
значений Х,
после окончания
решения с заданной
точностью.
-
вектор начальных
значений Х,
после окончания
решения с заданной
точностью.
Код возврата: retcode=0 при успешном решении u=1, при не успешном решении превышение допустимого числа итераций.
Память:
Требуется
дополнительный
массив
![]() для
хранения невязок.
для
хранения невязок.
Алгоритм
retcode=1
for Iter=1 to maxiter do (*расчет вектора невязок*)
rmax=0
for
i=1 to n do

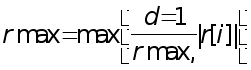
(*проверка на окончание итерационного процесса*)
if
rmax
return
(*найти улучшенное решение*)
for i=1 to n do
x[i]=x[i]+r[i]/A[i,j]
АЛГОРИТМ ГАУССА-ЗЕЙДЕЛЯ
Входные
параметры:
![]()
( релаксационный коэффициент )
![]() -
точность решения,
-
точность решения,
maxiter- максимальное число итераций.
Входно-
выходные параметры:
![]() -
вектор начальных
значений X,
после
окончания;
решение с заданной
точностью.
-
вектор начальных
значений X,
после
окончания;
решение с заданной
точностью.
Алгоритм
retcode=1
for iter=1 to maxiter do
rmax=0
(*улучшить решение*)
for i=1 to n do
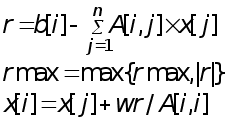
(*проверка на окончание итерационного процесса*)
if
rmax
retcode=0
return

program GAUS1(input,output);
type
matrix=array[1..100,1..100] of real;
vektor=array[1..100] of real;
var
a:matrix;
x,b,y:vektor;
n:integer;
ret_code:integer;
procedure geradlini(var a:matrix;var b,y:vektor;var n:integer);
var
s:real;j,i:integer;
begin
for i:=1 to n do
begin
s:=0;
for j:=1 to (i-1) do
s:=s+a[i,j]*y[j];
y[i]:=b[i]-s;
end;
end;
procedure ruckgang(var a:matrix;var y,x:vektor;var n:integer);
var
s:real;i,j:integer;
begin
s:=0;
for i:=n downto 1 do
begin
s:=0;
for j:=(i+1) to n do
s:=s+a[i,j]*x[j];
x[i]:=(y[i]-s)/a[i,i];
end;
end;
procedure vvod(var a:matrix;var b:vektor;var n:integer);
var
i,j:integer;
q:real;
begin
writeln('Введите количество точек на интервал: ');
readln(n);
for i:=1 to n do
begin
for j:=1 to n do
a[i,j]:=0;
a[i,i]:=(-2);
end;
for i:=1 to (n-1) do
a[i,i+1]:=1;
for i:=2 to n do
a[i,i-1]:=1;
q:=sqr(2/n);
for i:=1 to n do
if i<>n then b[i]:=q else b[i]:=(q-2);
end;
procedure triangul(var a:matrix;var b:vektor;
var ret_code:integer;n:integer);
label 1;
var
eps,buf,max,c:real;
k,imax,i,j:integer;
begin
ret_code:=1;
eps:=1;
buf:=1+eps;
while buf>1.0 do
begin
eps:=eps/2;
buf:=1+eps;
end;
buf:=n*eps;
for k:=1 to (n-1) do
begin
max:=a[k,k];
imax:=k;
for i:=k to n do
if a[i,k]>max then
begin
max:=a[i,k];
imax:=i;
end;
if a[imax,k]>buf then
begin
for j:=1 to n do
begin
c:=a[imax,j];
a[imax,j]:=a[k,j];
a[k,j]:=c;
end;
c:=b[imax];
b[imax]:=b[k];
b[k]:=c;
for i:=(k+1) to n do
begin
a[i,k]:=a[i,k]/a[k,k];
for j:=(k+1) to n do
a[i,j]:=a[i,j]-a[i,k]*a[k,j];
end;
end
else
begin
ret_code:=0;
goto 1
end;
1: end;
end;
procedure vivod(var x:vektor;var n:integer);
var
i:integer;
begin
for i:=1 to n do
writeln('x',i:1,'=',x[i],' ');
end;
begin
vvod(a,b,n);
triangul(a,b,ret_code,n);
if ret_code=1 then
begin
geradlini(a,b,y,n);
ruckgang(a,y,x,n);
vivod(x,n);
end
else
writeln('Матрица вырожденна');
end.
program GAUS2(input,output);
type
matrix=array[1..100,1..100] of real;
vektor=array[1..100] of real;
var
a:matrix;
x,b,y:vektor;
n:integer;
ret_code:integer;
procedure geradlini(var a:matrix;var b,y:vektor;
var n:integer);
var
s:real;j,i:integer;
begin
for i:=1 to n do
begin
s:=0;
for j:=1 to (i-1) do
s:=s+a[i,j]*y[j];
y[i]:=b[i]-s;
end;
end;
procedure ruckgang(var a:matrix;var y,x:vektor;
var n:integer);
var
s:real;i,j:integer;
begin
s:=0;
for i:=n downto 1 do
begin
s:=0;
for j:=(i+1) to n do
s:=s+a[i,j]*x[j];
x[i]:=(y[i]-s)/a[i,i];
end;
end;
procedure vvod(var a:matrix;var b:vektor;
var n:integer);
var
i,j:integer;
q:real;
begin
writeln('Введите количество точек на интервал: ');
readln(n);
q:=(-2+sqr(0.5/n)*(sqr(4*arctan(1))/4));
for i:=1 to n do
begin
for j:=1 to n do
a[i,j]:=0;
a[i,i]:=(q);
end;
for i:=1 to (n-1) do
a[i,i+1]:=1;
for i:=2 to n do
a[i,i-1]:=1;
for i:=1 to n do
if i<>n then b[i]:=0 else b[i]:=(-sqr(2)/2);
end;
procedure triangul(var a:matrix;var b:vektor;var ret_code:integer;
n:integer);
label 1;
var
eps,buf,max,c:real;
k,imax,i,j:integer;
begin
ret_code:=1;
eps:=1;
buf:=1+eps;
while buf>1.0 do
begin
eps:=eps/2;
buf:=1+eps;
end;
buf:=n*eps;
for k:=1 to (n-1) do
begin
max:=a[k,k];
imax:=k;
for i:=k to n do
if a[i,k]>max then
begin
max:=a[i,k];
imax:=i;
end;
if a[imax,k]>buf then
begin
for j:=1 to n do
begin
c:=a[imax,j];
a[imax,j]:=a[k,j];
a[k,j]:=c;
end;
c:=b[imax];
b[imax]:=b[k];
b[k]:=c;
for i:=(k+1) to n do
begin
a[i,k]:=a[i,k]/a[k,k];
for j:=(k+1) to n do
a[i,j]:=a[i,j]-a[i,k]*a[k,j];
end;
end
else
begin
ret_code:=0;
goto 1
end;
1: end;
end;
procedure vivod(var x:vektor;var n:integer);
var i:integer;
begin
for i:=1 to n do
writeln('x',i:1,'=',x[i]);
end;
begin
vod(a,b,n);
triangul(a,b,ret_code,n);
if ret_code=1 then
begin
geradlini(a,b,y,n);
ruckgang(a,y,x,n);
vivod(x,n);
end
else
writeln('Матрица вырождена ');
end.
program jakobi1(input,output);
type
vektor=array[1..100] of real;
var
r,y:vektor;
z,ret_code,maxiter:integer;
eps:real;
procedure vvod(var z,maxiter:integer;var eps:real);
begin
writeln('Введите кол-во точек на интервал');
readln(z);
writeln('Введите точность');
readln(eps);
writeln('Введите кол-во итераций');
readln(maxiter);
end;
procedure ren(var r,y:vektor;var z,ret_kode,maxiter:integer;var eps:real);
label 1;
var
iter,i:integer;
rmax,q:real;
begin
q:=sqr(2/z);
for i:=1 to z do
y[i]:=1;
ret_code:=0;
for iter:=1 to maxiter do {c.1}
begin
rmax:=0;
for i:=1 to z do {c.2}
begin
if i=1 then
begin
r[i]:=q-(-2*y[1]+y[2]);
if
rmax rmax:=abs(r[i]); end; if
i=z then begin r[z]:=(-2+q)-(y[z-1]-2*y[z]); if
rmax rmax:=abs(r[i]); end; if(i<>1)and(i<>z)
then begin r[i]:=q-(y[i-1]-2*y[i]+y[i+1]); if
rmax rmax:=abs(r[i]); end; end;{c.2} if
rmax<=eps then goto
1 else for
i:=1 to z do y[i]:=y[i]+r[i]/(-2); end;
{c.1} ret_code:=1; 1: end; procedure
vivod(var y:vektor;var z:integer); var i:integer; ch:char; begin for
i:=1 to z do writeln('y',i:1,y[i]); end; begin vvod(z,maxiter,eps); ren(r,y,z,ret_code,maxiter,eps); if
ret_code=0 then vivod(y,z) else writeln('Превышено
допустимое
число итераций'); end.
program
jakobi2(input,output); type vektor=array[1..100]
of real; var r,y:vektor; z,ret_code,maxiter:integer; eps:real; procedure
vvod(var z,maxiter:integer;var eps:real); begin writeln('Введите
кол-во точек
на интервал'); readln(z); writeln('Введите
точность'); readln(eps); writeln('Введите
кол-во итераций'); readln(maxiter); end; procedure
ren(var r,y:vektor;var z,ret_kode,maxiter:integer;var eps:real); label
1; var iter,i:integer; rmax,q:real; begin q:=sqr(2/z); for
i:=1 to z do y[i]:=1; ret_code:=0; for
iter:=1 to maxiter do begin rmax:=0; for
i:=1 to z do begin if
i=1 then begin r[i]:=q-(-2*y[1]+y[2]); if
rmax rmax:=abs(r[i]); end; if
i=z then begin r[z]:=(-2+q)-(y[z-1]-2*y[z]); if
rmax rmax:=abs(r[i]); end; if(i<>1)and(i<>z)
then
begin r[i]:=q-(y[i-1]-2*y[i]+y[i+1]); if
rmax end; end; if
rmax<=eps then goto 1 else for
i:=1 to z do y[i]:=y[i]+r[i]/q; end; ret_code:=1; 1:end; procedure
vivod(var y:vektor;var z:integer); var i:integer; begin for
i:=1 to z do writeln('y',i:1,y[i]); end; begin vvod(z,maxiter,eps); ren(r,y,z,ret_code,maxiter,eps); if
ret_code=0 then vivod(y,z) else write('Превышено
допустимое
число итераций'); end.
program
zeidel1(input,output); type vector=array[1..1000]
of real; var y:vector; z,retcode,maxiter:integer; eps:real; procedure
wod(var z,maxiter:integer;var eps:real); begin writeln; writeln('введите
количество
точек на интервал
'); readln(z); writeln('введите
точность
');readln(eps); writeln('введите
количество
итераций
');readln(maxiter); writeln('коофицент
релаксации
W,принят равный
1'); end; procedure
reshen(var y:vector;var z,retcode,maxiter:integer;var eps:real); label
1; var Iter,I:integer;R,Rmax,Q:real; begin Q:=sqr(2/z); for
i:=1 to z do y[i]:=1; retcode:=1; for
Iter:=1 to maxiter do begin Rmax:=0; for
i:=1 to z do begin if
i=1 then begin R:=Q-(-2*y[1]+y[2]); if
Rmax y[i]:=y[i]+R/(-2); end; if
i=z then begin R:=(-2+Q)-(y[z-1]-2*y[z]); if
Rmax y[i]:=y[i]+r/(-2); end; if
(I<>1) and (i<>z) then begin r:=Q-(y[i-1]-2*y[i]+y[i+1]); if
Rmax y[i]:=y[i]+R/-2; end; end; if
Rmax<=eps then begin retcode:=0; goto
1; end; end; 1:
end; procedure
vivod(var y:vector;var z:integer); var i:integer; begin for
i:=1 to z do write('y',i:2,'=',y[i]); end; begin wod(z,maxiter,eps); reshen(y,z,retcode,maxiter,eps); if
retcode=0 then vivod(y,z) else write('число
итераций'); end.
program
zeidel2(input,output); type vector=array[1..1000]
of real; var y:vector; z,retcode,maxiter:integer; eps:real; procedure
wod(var z,maxiter:integer;var eps:real); begin writeln; writeln('введите
количество
точек на интервал
'); readln(z); writeln('введите
точность
');readln(eps); writeln('введите
количество
итераций
');readln(maxiter); writeln('коофицент
релаксации
W,принят равный
1'); end; procedure
reshen(var y:vector;var z,retcode,maxiter:integer;var eps:real); label
1; var Iter,I:integer;R,Rmax,Q:real; begin Q:=(-2+sqr(0.5/z)*sqr(4*arctan(1))/4); for
i:=1 to z do y[i]:=1; retcode:=1; for
Iter:=1 to maxiter do begin Rmax:=0; for
i:=1 to z do begin if
i=1 then begin r:=-(q*y[1]+y[z]); if
Rmax y[i]:=y[i]+R/q; end; if
i=z then begin r:=-sqrt(z)/2-(y[z-1]+q*y[z]); if
Rmax y[i]:=y[i]+r/q; end; if
(I<>1) and (i<>z) then begin r:=-(y[i-1]+q*y[i]+y[i+1]); if
Rmax y[i]:=y[i]+R/q; end; end; if
Rmax<=eps then begin retcode:=0; goto
1; end; end; 1:
end; procedure
vivod(var y:vector;var z:integer); var i:integer; begin for
i:=1 to z do writeln
(i:1,'=',y[i],); end; begin wod(z,maxiter,eps); reshen(y,z,retcode,maxiter,eps); if
retcode=0 then vivod(y,z) else write('число
итераций'); end.
ИНСТРУКЦИЯ
ДЛЯ ПОЛЬЗОВАТЕЛЯ
Программа
Jacobi1
предназначена
для решения
уравнений
Программы
Zeidel1
и
Zeidel2,
также решают
уравнения
Вычисление
уравнений с
помощью итерационного
метода Якоби
требует времени
t=0(maxiter
Z),
где Z-
количество
точек на интервал,
а maxiter-
количество
итераций.
Вычисление
уравнений с
помощью метода
Гаусса требует
времени t=0(
Решение
с помощью метода
Гаусса требует
больше времени
чем решения
другими двумя
приведенными
способами.![]() .
Jacobi2
для
решения уравнений
.
Jacobi2
для
решения уравнений
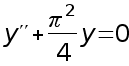 ,методом конечных
разностей
находят значение
,методом конечных
разностей
находят значение
![]() в точках
интервала (0.2)
максимальное
количество
точек на интервал
1000. Используется
массив для
хранения значений
вектора невязок
в точках
интервала (0.2)
максимальное
количество
точек на интервал
1000. Используется
массив для
хранения значений
вектора невязок
![]() .
В процедуре
reshen
находится
вектор невязок
r
[ i ].
Для первого
и последнего
уравнения
системы находят
вектора невязок
различными
способами. Для
остальных
уравнений
системы вектор
невязок находится
одинаково. Сама
матрица не
формируется
, т.е. для нахождения
вектора невязок
ее не нужно,
это видно из
текста программы.
.
В процедуре
reshen
находится
вектор невязок
r
[ i ].
Для первого
и последнего
уравнения
системы находят
вектора невязок
различными
способами. Для
остальных
уравнений
системы вектор
невязок находится
одинаково. Сама
матрица не
формируется
, т.е. для нахождения
вектора невязок
ее не нужно,
это видно из
текста программы.![]() и
и
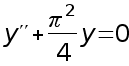 . Отличия от
Jacobi
состоит
только в том,
что отсутствует
массив для
вектора невязок.
Программы Gaus1
и
Gaus2
также
решают эти
уравнения,
только методом
Гаусса. В процедурах
vvod
задается количество
точек на интервал(max=100)
и формируются
матрицы в зависимости
от уравнения.
Процедура
triangul
разлагает
матрицу А на
две треугольные.
Процедура
geradlini-
прямой ход
метода Гаусса.
Процедура
ruckgang-
обратный ход.
Процедура
vivod-
выводит значения
. Отличия от
Jacobi
состоит
только в том,
что отсутствует
массив для
вектора невязок.
Программы Gaus1
и
Gaus2
также
решают эти
уравнения,
только методом
Гаусса. В процедурах
vvod
задается количество
точек на интервал(max=100)
и формируются
матрицы в зависимости
от уравнения.
Процедура
triangul
разлагает
матрицу А на
две треугольные.
Процедура
geradlini-
прямой ход
метода Гаусса.
Процедура
ruckgang-
обратный ход.
Процедура
vivod-
выводит значения
![]() .
.![]() ),
где N-
количество
точек на интервал.
),
где N-
количество
точек на интервал.