Реферат: Отрывок из учебника по теории систем и системному анализу
Администрации сайта и тем, кто
рискнет Скачать сей “труд”:
Заранее приношу свои извинения за
не очень хорошее распознавание
отсканированных страниц, но т. к.
в Инете информации именно на эту
тему немного (сам искал), то я все же
взял на себя смелость разместить
у вас эти страницы.
Заранее благодарю,
VITAS.
108
Глава 2
Основы оценки сложных систем
109
ты является монотонный характер функции полезности (ценности), построенной для каждой составляющей. Если при этом какая-либо из функций не монотонная, то это означает, что упущены одна или несколько составляющих ПИО.
Следующее важное требование к ПИО - измеримость его составляющих с помощью либо натурного эксперимента, либо моделей операции. Если рассматриваемая операция не позволяет это сделать, ее целесообразно разложить на подоперации, обеспечивающие измеримость составляющих. Процесс декомпозиции операции на подоперации может быть многоуровневым. Например, операцию «Решение задач управления» можно разделить на подоперации: «Решение задач планирования» и «Решение задач оперативного управления», а последние, в свою очередь, - на «Решение задач учета», «Решение задач контроля» и т.д.
При определении задач ПИО необходимо стремиться к ясности их физического смысла, т.е. чтобы они измерялись с помощью количественных мер, доступных для восприятия. Однако достичь этого удается не всегда. Тогда приходится вводить так называемые субъективные составляющие ПИО. Например, такое свойство людей, как обученность, обычно не может быть определено с помощью характеристик, имеющих физический смысл. В этом случае часто вводят некоторую искусственную шкалу. Другой способ обеспечения измеримости составляющих ПИО переход к показателям-заменителям, косвенно характеризующим рассматриваемое свойство. Требование ясности физического смысла ограничивает возможности агрегирования частных показателей в один критерий. Так, например, не имеет физического смысла обобщенный скалярный показатель, составленный из частных показателей результативности, ресурсоемкости и оперативности.
Важным требованием к ПИО является минимизация его размерности, т. е. обеспечение неизбыточного набора составляющих. С ростом количества составляющих резко возрастает трудоемкость построения функции эффективности.
И, наконец, в группу основных требований к составляющим ПИО обычно вводят их относительно высокую чувствительность к изменениям значений управляемых характеристик.
Таким образом, набор составляющих ПИО может быть определен различными способами, поскольку к настоящему време-
ни еще не существует формальной теории, обеспечивающей объективное решение этой задачи. Два лица, принимающие решение на одну и ту же операцию, могут определить различный состав ПИО. Важно лишь то, что, используя различные ПИО, они должны выбрать одинаковое решение - оптимальное.
2.4.
МЕТОДЫ КАЧЕСТВЕННОГО ОЦЕНИВАНИЯ СИСТЕМ
Методы оценивания систем разделяются на качественные и количественные.
Качественные методы используются на начальных этапах моделирования, если реальная система не может быть выражена в количественных характеристиках, отсутствуют описания закономерностей систем в виде аналитических зависимостей. В результате такого моделирования разрабатывается концептуальная модель системы.
Количественные методы используются на последующих этапах моделирования для количественного анализа вариантов системы.
Между этими крайними методами имеются и такие, с помощью которых стремятся охватить все этапы моделирования от постановки задачи до оценки вариантов, но для представления задачи оценивания привлекают разные исходные концепции и терминологию с разной степенью формализации. К ним относят:
• кибернетический
подход к разработке адаптивных систем
управления,
проектирования и принятия решений (который ис
ходит из теории автоматического управления применительно к
организационным
системам);
• информационно-гносеологический
подход к моделирова
нию
систем (основанный на общности процессов отражения, по
знания
в системах различной физической природы);
• структурный и
объектно-ориентированные подходы сис
темного
анализа;
• метод ситуационного моделирования;
• метод имитационного динамического моделирования.
110
Глава 2
Основы оценки сложных систем
111
Такие методы позволяют разрабатывать как концептуальные, так и строго формализованные модели, обеспечивающие требуемое качество оценки систем.
Во всех методах смысл задачи оценивания состоит в сопоставлении рассматриваемой системе (альтернативе) вектора из критериального пространства Кт, координаты точек которого рассматриваются как оценки по соответствующим критериям.
Например, пусть множество Q разбито на / подмножеств Q1, Q2, ..., qi- Для элемента х е Q необходимо указать, к какому из подмножеств Qi он относится. В этом случае элементу х сопоставляется одно из чисел 1, 2, ...,l, в зависимости от номера содержащего его подмножества.
Простейшей формой задачи оценивания является обычная задача измерения, когда оценивание есть сравнение с эталоном, а решение задачи находится подсчетом числа эталонных единиц в измеряемом объекте. Например, пусть х - отрезок, длину которого надо измерить. В этом случае отрезку сопоставляется действительное число ф (х) - его длина.
Более сложные задачи оценивания разделяются на задачи: парного сравнения, ранжирования, классификации, численной оценки.
Задача парного сравнения заключается в выявлении лучшего из двух имеющихся объектов. Задача ранжирования - в упорядочении объектов, образующих систему, по убыванию (возрастанию) значения некоторого признака. Задача классификации - в отнесении заданного элемента к одному из подмножеств. Задача численной оценки - в сопоставлении системе одного или нескольких чисел.
Перечисленные задачи могут быть решены непосредственно лицом, принимающим решение, или с помощью экспертов - специалистов в исследуемой области. Во втором случае решение задачи оценивания называется экспертизой.
Качественные методы измерения и оценивания характеристик систем, используемые в системном анализе, достаточно многочисленны и разнообразны.
К основным методам качественного оценивания систем относят:
• методы типа мозговой атаки или коллективной генерации идей;
типа сценариев; экспертных оценок; типа Дельфи; типа дерева целей; морфологические методы.
2.4.1.
МЕТОДЫ ТИПА «МОЗГОВАЯ АТАКА» ИЛИ «КОЛЛЕКТИВНАЯ ГЕНЕРАЦИЯ ИДЕЙ»
Концепция «мозговая атака» получила широкое распространение с начала 50-х гг. как метод тренировки мышления, нацеленный на открытие новых идей и достижение согласия группы людей на основе интуитивного мышления. Методы этого типа известны также под названиями «мозговой штурм», «конференция идей», «коллективная генерация идей» (КГИ).
Обычно при проведении сессий КГИ стараются выполнять определенные правила, суть которых:
• обеспечить как можно
большую свободу мышления участ
ников
КГИ и высказывания ими новых идей;
• приветствовать любые
идеи, даже если вначале они кажут
ся
сомнительными или абсурдными (обсуждение и оценка идей
производятся
позднее);
• не допускать критики
любой идеи, не объявлять ее ложной
и не прекращать обсуждение;
• желательно
высказывать как можно больше идей, особен
но
нетривиальных.
В зависимости от принятых правил и жесткости их выполнения различают прямую «мозговую атаку», метод обмена мнениями и другие виды коллективного обсуждения идей и вариантов принятия решений. В последнее время стараются ввести правила, помогающие сформировать некоторую систему идей, т.е. предлагается, например, считать наиболее ценными те из них, которые связаны с ранее высказанными и представляют собой их развитие и обобщение. Участникам не разрешается зачитывать списки предложений, которые они подготовили заранее. В то же время, чтобы предварительно нацелить участника на обсуждаемый вопрос, при организации сессий КГИ заранее или перед на-
112
Глава 2
Основы оценки сложных систем
113
чалом сессии участникам представляется некоторая предварительная информация об обсуждаемой проблеме в письменной или устной форме. Подобием сессий КГИ можно считать разного рода совещания - конструктораты, заседания научных советов по проблемам, заседания специально создаваемых временных комиссий и другие собрания компетентных специалистов.
Так как на практике трудно собрать специалистов ввиду их занятости по основной работе, желательно привлекать компетентных специалистов, не требуя обязательного их присутствия на общих собраниях КГИ и устного высказывания своих соображений хотя бы на первом этапе системного анализа при формировании предварительных вариантов.
2.4.2. МЕТОДЫ ТИПА СЦЕНАРИЕВ
Методы подготовки и согласования представлений о проблеме или анализируемом объекте, изложенные в письменном виде, получили название сценария. Первоначально этот метод предполагал подготовку текста, содержащего логическую последовательность событий или возможные варианты решения проблемы, упорядоченные по времени. Однако требование временных координат позднее было снято, и сценарием стали называть любой документ, содержащий анализ рассматриваемой проблемы или предложения по ее решению независимо от того, в какой форме он представлен.
Сценарий не только предусматривает содержательные рассуждения, которые помогают не упустить детали, обычно не учитываемые при формальном представлении системы (в этом и заключалась первоначально основная роль сценария), но и содержит результаты количественного технико-экономического или статистического анализа с предварительными выводами, которые можно получить на их основе. Группа экспертов, подготавливающих сценарии, пользуется правом получения необходимых справок от организаций, консультаций специалистов. Понятие сценариев расширяется в направлении как областей применения, так и форм представления и методов их разработки: в сценарий не только вводятся количественные параметры и устанавливаются
их взаимосвязи, но и предлагаются методики составления сценариев с использованием ЭВМ.
\ На практике по типу сценариев разрабатывались прогнозы в некоторых отраслях промышленности. В настоящее время раз-ндвидностью сценариев можно считать предложения к комплексным программам развития отраслей народного хозяйства, под-готавливаемыеt организациями или специальными комиссиями. Существенную помощь в подготовке сценариев оказывают специалисты по системному анализу. Весьма перспективной представляется разработка специализированных информационно-поисковых систем, накапливающих прогнозную информацию по данной отрасли и по смежным отраслям.
Сценарий является предварительной информацией, на основе которой проводится дальнейшая работа по прогнозированию или разработке вариантов проекта. Таким образом, сценарий помогает составить представление о проблеме, а затем приступить к более формализованному представлению системы в виде графиков, таблиц для проведения других методов системного анализа.
2.4.3. МЕТОДЫ ЭКСПЕРТНЫХ ОЦЕНОК
Группа методов экспертных оценок наиболее часто используется в практике оценивания сложных систем на качественном уровне. Термин «эксперт» происходит от латинского слова expert - «опытный».
При использовании экспертных оценок обычно предполагается, что мнение группы экспертов надежнее, чем мнение отдельного эксперта. В некоторых теоретических исследованиях отмечается, что это предположение не является очевидным, но одновременно утверждается, что при соблюдении определенных требований в большинстве случаев групповые оценки надежнее индивидуальных. К числу таких требований относятся: распределение оценок, полученных от экспертов, должно быть «гладким»; две групповые оценки, данные двумя одинаковыми подгруппами, выбранными случайным образом, должны быть близки.
8—20
114
Глава 2
Основы оценки сложных систем
115
Все множество проблем, решаемых методами экспертных оценок, делится на два класса. К первому классу относятся такие, в отношении которых имеется достаточное обеспечение информацией. При этом методы опроса и обработки основываются на использовании принципа «хорошего измерителя», т.е. эксперт источник достоверной информации; групповое мнение экспертов близко к истинному решению. Ко второму классу относятся проблемы, в отношении которых знаний для уверенности и справедливости указанных гипотез недостаточно. В этом случае экспертов нельзя рассматривать как «хороших измерителей» и необходимо осторожно подходить к обработке результатов экспертизы.
Экспертные оценки несут в себе как узкосубъективные черты, присущие каждому эксперту, так и коллективно-субъективые, присущие коллегии экспертов. И если первые устраняются в процессе обработки индивидуальных экспертных оценок, то вторые не исчезают, какие бы способы обработки не применялись.
Этапы экспертизы формирование цели, разработка процедуры экспертизы, формирование группы экспертов, опрос, анализ и обработка информации.
При формулировке цели экспертизы разработчик должен выработать четкое представление о том, кем и для каких целей будут использованы результаты.
При обработке материалов коллективной экспертной оценки используются методы теории ранговой корреляции. Для количественной оценки степени согласованности мнений экспертов применяется коэффициент конкордации W, который позволяет оценить, насколько согласованы между собой ряды предпочтительности, построенные каждым экспертом. Его значение находится в пределах 0 < W < I, где W = 0 означает полную противоположность, a W = 1 - полное совпадение ранжировок. Практически достоверность считается хорошей, если W = 0,7-0,8.
Небольшое значение коэффициента конкордации, свидетельствующее о слабой согласованности мнений экспертов, является следствием того, что в рассматриваемой совокупности экспертов действительно отсутствует общность мнений или внутри рассматриваемой совокупности экспертов существуют группы с высокой согласованностью мнений, однако обобщенные мнения таких групп противоположны.
Для наглядности представления о степени согласованности мнений двух любых экспертов А и В служит коэффициент парной ранговой корреляции р, он принимает значения -1 < р < +1. Значение р = +1 соответствует полному совпадению оценок в рангах двух экспертов (полная согласованность мнений двух экспертов), а значение р = -1 -двум взаимно противоположным ранжировкам важности свойств (мнение одного эксперта противоположно мнению другого).
Тип используемых процедур экспертизы зависит от задачи оценивания.
К наиболее употребительным процедурам экспертных измерений относятся:
• ранжирование;
• парное сравнивание;
• множественные сравнения;
• непосредственная оценка;
• Черчмена-Акоффа;
• метод Терстоуна;
• метод фон Неймана-Моргенштерна.
Целесообразность применения того или иного метода во многом определяется характером анализируемой информации. Если оправданы лишь качественные оценки объектов по некоторым качественным признакам, то используются методы ранжирования, парного и множественного сравнения.
Если характер анализируемой информации таков, что целесообразно получить численные оценки объектов, то можно использовать какой-либо метод численной оценки, начиная от непосредственных численных оценок и кончая более тонкими методами Терстоуна и фон Неймана-Моргенштерна.
При описании каждого из перечисленных методов будет предполагаться, что имеется конечное число измеряемых или оцениваемых альтернатив (объектов) А = {а^ ... ,ап} и сформулированы один или несколько признаков сравнения, по которым осуществляется сравнение свойств объектов. Следовательно, методы измерения будут различаться лишь процедурой сравнения объектов. Эта процедура включает построение отношений между объектами эмпирической системы, выбор преобразования ф и определение типа шкал измерений. С учетом изложенных выше обстоятельств рассмотрим каждый метод измерения. 8*
116
Глава 2
Основы оценки сложных систем
117
Ранжирование. Метод представляет собой процедуру упорядочения объектов, выполняемую экспертом. На основе знаний и опыта эксперт располагает объекты в порядке предпочтения, руководствуясь одним или несколькими выбранными показателями сравнения. В зависимости от вида отношений между объектами возможны различные варианты упорядочения объектов.
Рассмотрим эти варианты. Пусть среди объектов нет одинаковых по сравниваемым показателям, т.е. нет эквивалентных объектов. В этом случае между объектами существует только отношение строгого порядка. В результате сравнения всех объектов по отношению строгого порядка составляется упорядоченная последовательность а{ > а2> ... > aN, где объект с первым номером является наиболее предпочтительным из всех объектов, объект со вторым номером менее предпочтителен, чем первый объект, но предпочтительнее всех остальных объектов и т.д. Полученная система объектов с отношением строгого порядка при условии сравнимости всех объектов по этому отношению образует полный строгий порядок. Для этого отношения доказано существование числовой системы, элементами которой являются действительные числа, связанные между собой отношением неравенства >. Это означает, что упорядочению объектов соответствует упорядочение чисел х, >... > xn, где х,—ф Ц.). Возможна и обратная последовательность х, <... < xn, в которой наиболее предпочтительному объекту приписывается наименьшее число и по мере убывания предпочтения объектам приписываются большие числа.
Соответствие перечисленных последовательностей, т.е. их гомоморфизм, можно осуществить, выбирая любые числовые представления. Единственным ограничением является монотонность преобразования. Следовательно, допустимое преобразование при переходе от одного числового представления к другому должно обладать свойством монотонности. Таким свойством допустимого преобразования обладает шкала порядков, поэтому ранжирование объектов есть измерение в порядковой шкале.
В практике ранжирования чаще всего применяется числовое представление последовательности в виде натуральных чисел:
т.е. используется числовая последовательность. Числа х,, х2,..., xn в этом случае называются рангами и обычно обозначаются
буквами г, , г2, ... , rN. Применение строгих численных отношений «больше» (>), «меньше» (<) или «равно» (=) не всегда позволяет установить порядок между объектами. Поэтому наряду с ними используются отношения для определения большей или меньшей степени какого-то качественного признака (отношения частичного порядка, например полезности), отношения типа «более предпочтительно» (>), «менее предпочтительно» (<), «равноценно» ( = ) или «безразлично» (~). Упорядочение объектов при этом может иметь, например, следующий вид:
Такое упорядочение образует нестрогий линейный порядок.
Для отношения нестрогого линейного порядка доказано существование числовой системы с отношениями неравенства и равенства между числами, описывающими свойства объектов. Любые две числовые системы для нестрогого линейного порядка связаны между собой монотонным преобразованием. Следовательно, ранжирование при условии наличия эквивалентных объектов представляет собой измерение также в порядковой шкале.
В практике ранжирования объектов, между которыми допускаются отношения как строгого порядка, так и эквивалентности, числовое представление выбирается следующим образом. Наиболее предпочтительному объекту присваивается ранг, равный единице, второму по предпочтительности - ранг, равный двум, и т.д. Для эквивалентных объектов удобно с точки зрения технологии последующей обработки экспертных оценок назначать одинаковые ранги, равные среднеарифметическому значению рангов, присваиваемых одинаковым объектам. Такие ранги называют связанными рангами. Для приведенного примера упорядочения на основе нестрогого линейного порядка при N = 10 ранги объектов д3 , а4 , а5 будут равными г3 = г4 = г5 = (3+4+5) /3 = 4.
В этом же примере ранги объектов й9, а,0 также одинаковы и равны среднеарифметическому r9 = rlo = (9+10) 12 = 9,5. Связанные ранги могут оказаться дробными числами. Удобство использования связанных рангов заключается в том, что сумма рангов N объектов равна сумме натуральных чисел от единицы до N. При этом любые комбинации связанных рангов не изменяют эту сумму. Данное обстоятельство существенно упрощает обработку результатов ранжирования при групповой экспертной оценке.
118
Глава 2
Основы оценки сложных систем
119
При групповом ранжировании каждый S-й эксперт присваивает каждому /-му объекту ранг rjs. В результате проведения экспертизы получается матрица рангов | | ris \ \ размерности Nk, где k- число экспертов; N- число объектов; S=l,k;i=l,N. Результаты группового экспертного ранжирования удобно представить в виде табл. 2.5.
Аналогичный вид имеет таблица, если осуществляется ранжирование объектов одним экспертом по нескольким показателям сравнения. При этом в таблице вместо экспертов в соответствующих графах указываются показатели. Напомним, что ранги объектов определяют только порядок расположения объектов по показателям сравнения. Ранги как числа не дают возможности сделать вывод о том, на сколько или во сколько раз предпочтительнее один объект по сравнению с другим.
Таблица 2.5
Результаты группового ранжирования
| Объект | э, |
Э2 |
... | э* |
|
Й1 |
г\\ |
'12 | ... |
r\k |
| «2 |
Г21 |
'22 | ... |
r2k |
| ... |
... |
... | ||
|
ап |
rnl |
ГЛ |
... |
rnk |
Достоинство ранжирования как метода экспертного измерения - простота осуществления процедур, не требующая трудоемкого обучения экспертов. Недостатком ранжирования является практическая невозможность упорядочения большого числа объектов. Как показывает опыт, при числе объектов, большем 10-15, эксперты затрудняются в построении ранжировки. Это объясняется тем, что в процессе ранжирования эксперт должен установить взаимосвязь между всеми объектами, рассматривая их как единую совокупность. При увеличении числа объектов количество связей между ними растет пропорционально квадрату числа объектов. Сохранение в памяти и анализ большой совокупности взаимосвязей между объектами ограничиваются психологическими возможностями человека. Психология утвержда-
ет, что оперативная память человека позволяет оперировать в среднем не более чем 7 ± 2 объектами одновременно. Поэтому при ранжировании большого числа объектов эксперты могут допускать существенные ошибки.
Парное сравнение. Этот метод представляет собой процедуру установления предпочтения объектов при сравнении всех возможных пар. В отличие от ранжирования, в котором осуществляется упорядочение всех объектов, парное сравнение объектов является более простой задачей. При сравнении пары объектов возможно либо отношение строгого порядка, либо отношение эквивалентности. Отсюда следует, что парное сравнение так же, как и ранжирование, есть измерение в порядковой шкале.
В результате сравнения пары объектов а;, а/ эксперт упорядочивает ее, высказывая либо я, >- а-, либо а, > at, либо at ~ а . Выбор числового представления ф(й(.) можно произвести так: если ai X а» то ф (а(.) > ф (о ); если предпочтение в паре обратное, то знак неравенства заменяется на обратный, т.е. ф (а,) < ф (а,). Если объекты эквивалентны, то можно считать, что ф (я,-) = ф (а ).
В практике парного сравнения используются следующие числовые представления:
| (2.1) |
|
Хн = • |
|
( |
I, если а/ >- dj или at ~ Oj\ О, если а, ч о/, i,j = l,N;
| (2.2) |
2, если а,- >- ау-; 1, если а,- ~ uji О, если а; ч а .•, /, J = 1, N.
Результаты сравнения всех пар объектов удобно представлять в виде матрицы. Пусть, например, имеются пять объектов а,, а2, а3, а4, а5 и проведено парное сравнение этих объектов по предпочтительности. Результаты сравнения представлены в виде
Используя числовое представление (2.1), составим матрицу измерения результатов парных сравнений (табл. 2.6).
120
Глава 2
Основы оценки сложных систем
121
| Таблица 2.7 |
Таблица 2.6
|
Результаты измерения пяти объектов |
|
а\ |
°2 |
аз |
Й4 |
°5 | |
|
а\ |
\ |
2 | 2 | 2 | 0 |
|
°2 |
0 | 1 | 2 | 2 | 0 |
|
Й3 |
0 | 0 | 1 | 1 | 0 |
| «4 | 0 | 0 | 1 | 1 | 0 |
|
°5 |
2 | 2 | 2 | 2 | 1 |
Матрица парных сравнений
| «1 | °2 |
аЗ |
°4 |
а5 |
|
| «1 | 1 | 1 | 1 | 1 | 0 |
|
а2 |
0 | 1 | 1 | 1 | 0 |
|
аз |
0 | 0 | 1 | 1 | 0 |
|
а4 |
0 | 0 | 1 | 1 | 0 |
| °5 | 1 | 1 | 1 | 1 | 1 |
В табл. 2.6 на диагонали всегда будут расположены единицы, поскольку объект эквивалентен себе. Представление (2.2) характерно для отображения результатов спортивных состязаний. За выигрыш даются два очка, за ничью одно и за проигрыш ноль очков (футбол, хоккей и т.п.). Предпочтительность одного объекта перед другим трактуется в данном случае как выигрыш одного участника турнира у другого. Таблица результатов измерения при использовании числового представления не отличается от таблиц результатов спортивных турниров за исключением диагональных элементов (обычно в турнирных таблицах диагональные элементы заштрихованы). В качестве примера в табл. 2.7 приведены результаты измерения пяти объектов с использованием представления (2.2), соответствующие табл. 2.6.
Вместо представления (2.2) часто используют эквивалентное ему представление
|
хн -1 |
+ 1, если cn>aj', О, если ai~dj', -1, если ai^aj-, i,j = l,N,
которое получается из (2.2) заменой 2 на +1, 1 на 0 и 0 на 1.
Если сравнение пар объектов производится отдельно по различным показателям или сравнение осуществляет группа экспертов, то по каждому показателю или эксперту составляется своя таблица результатов парных сравнений. Сравнение во всех воз-
можных парах не дает полного упорядочения объектов, поэтому возникает задача ранжирования объектов по результатам их парного сравнения.
Однако, как показывает опыт, эксперт далеко не всегда последователен в своих предпочтениях. В результате использования метода парных сравнений эксперт может указать, что объект а, предпочтительнее объекта а2, а2 предпочтительнее объекта а3 и в то же время а3 предпочтительнее объекта а,.
В случае разбиения объекта на классы эксперт может к одному классу отнести пары al и а2, а2 и а3, но в то же время объекты а, и а3 отнести к различным классам. Такая непоследовательность эксперта может объясняться различными причинами: сложностью задачи, неочевидностью предпочтительности объектов или разбиения их на классы (в противном случае, когда все очевидно, проведение экспертизы необязательно), недостаточной компетентностью эксперта, недостаточно четкой постановкой задачи, многокритериальностью рассматриваемых объектов и т.д.
Непоследовательность эксперта приводит к тому, что в результате парных сравнений при определении сравнительной предпочтительности объектов мы не получаем ранжирования и даже отношений частичного порядка не выполнено свойство транзитивности.
Если целью экспертизы при определении сравнительной предпочтительности объектов является получение ранжирования или частичного упорядочения, необходима их дополнительная идентификация. В этих случаях имеет смысл в качестве результирующего отношения выбирать отношение заданного типа, ближайшее к полученному в эксперименте.
Множественные сравнения. Они отличаются от парных тем, что экспертам последовательно предъявляются не пары, а тройки, четверки,..., n-ки («<ЛО объектов. Эксперт их упорядочивает по важности или разбивает на классы в зависимости от целей экспертизы. Множественные сравнения занимают промежуточное положение между парными сравнениями и ранжированием. С одной стороны, они позволяют использовать больший, чем при парных сравнениях, объем информации для определения экспертного суждения в результате одновременного соотнесения объекта не с одним, а с большим числом объектов. С другой стороны, при ранжировании объектов их может оказаться слишком мно-
122
Глава 2
Основы оценки сложных систем
123
го, что затрудняет работу эксперта и сказывается на качестве результатов экспертизы. В этом случае множественные сравнения позволяют уменьшить до разумных пределов объем поступающей к эксперту информации.
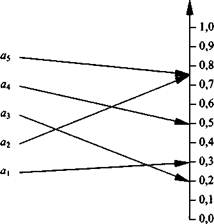
Непосредственная оценка. Метод заключается в присваивании объектам числовых значений в шкале интервалов. Эксперту необходимо поставить в соответствие каждому объекту точку на определенном отрезке числовой оси. При этом необходимо, чтобы эквивалентным объектам приписывались одинаковые числа. На рис. 2.6 в качестве примера приведено такое представление для пяти объектов на отрезок числовой оси [0,1].
Поскольку за начало отсчета выбрана нулевая точка, то в данном примере измерение производится в шкале отношений. Эксперт соединяет каждый объект линией с точкой числовой оси и получает следующие числовые представления объектов (см. рис. 2.6):
Ф (а,) = 0,28; <р (а2) = <р (а5) = 0,75; ф (а3) = 0,2; ф (aj = 0,5.
|
|
| Оцениваемые объекты |
| Шкала отношений |
|
Рис. 2.6. Пример сравнения пяти объектов по шкале |
Измерения в шкале интервалов могут быть достаточно точными при полной информированности экспертов о свойствах объектов. Эти условия на практике встречаются редко, поэтому для измерения применяют балльную оценку. При этом вместо
непрерывного отрезка числовой оси рассматривают участки, которым приписываются баллы.
Эксперт, приписывая объекту балл, тем самым измеряет его с точностью до определенного отрезка числовой оси. Применяются 5-, 10- и 100-балльные шкалы.
Метод Черчмена Акоффа (последовательное сравнение). Этот метод относится к числу наиболее популярных при оценке альтернатив. В нем предполагается последовательная корректировка оценок, указанных экспертами. Основные предположения, на которых основан метод, состоят в следующем:
• каждой альтернативе at(i = \,N) ставится в
соответствие
действительное
неотрицательное число ф (аг );
• если альтернатива ai предпочтительнее
альтернативы а, ,
то ф
(а,.) > ф (а.), если же альтернативы яг и я равноценны,
тоф(о(.)
= ф(а/);
• если ф (я,.) и ф (а
.) оценки альтернатив а/ и а •, то ф (а(.) + ф (а)
соответствует
совместному осуществлению альтернатив а/ и а..
Наиболее сильным является последнее предположение об адди
тивности оценок альтернатив.
Согласно методу Черчмена-Акоффа альтернативы at, a2, ... , aN ранжируются по предпочтительности. Пусть для удобства изложения альтернатива al наиболее предпочтительна, за ней следует а2 и т.д. Эксперт указывает предварительные численные оценки ф (flj) для каждой из альтернатив. Иногда наиболее предпочтительной альтернативе приписывается оценка 1, остальные оценки располагаются между 0 и 1 в соответствии с их предпочтительностью. Затем эксперт производит сравнение альтернативы al и суммы альтернатив а2, ••• > ан- Если а\ предпочтительнее, то эксперт корректирует оценки так, чтобы
N
В противном случае должно выполняться неравенство
Если альтернатива а; оказывается менее предпочтительной, то для уточнения оценок она сравнивается по предпочтению с суммой альтернатив а2,а3, ... , aN_, и т.д. После того как альтер-
124
Глава 2
|
\pat ;, (1-р)а/] предпочтительнее, чем \р'а{, (1-р') в/], если/»/?' и др. Если указанная система предпочтений выполнена, то для каждой из набора основных альтернатив al , а2, ... , aN определяются числа jf], х2, ... , xn, характеризующие численную оценку смешанных альтернатив. Численная оценка смешанной альтернативы \pl alt р2а2, ... , PN aN] равна х, />, + х2р2 + . . . + xNpN. Смешанная альтернатива \р^а^ р2а2, ... , pNaN] предпочтительнее смешанной альтернативы \р\ а,, р "2 аг , ... , p'N aN], если |
натива al оказывается предпочтительнее суммы альтернатив а2,..., ak (к > 2), она исключается из рассмотрения, а вместо оценки альтернативы а, рассматривается и корректируется оценка альтернативы я2- Процесс продолжается до тех пор, пока откорректированными не окажутся оценки всех альтернатив.
При достаточно большом N применение метода Черчмена-Акоффа становится слишком трудоемким. В этом случае целесообразно разбить альтернативы на группы, а одну из альтернатив, например максимальную, включить во все группы. Это позволяет получить численные оценки всех альтернатив с помощью оценивания внутри каждой группы.
Метод Черчмена-Акоффа является одним самых эффективных. Его можно успешно использовать при измерениях в шкале отношений. В этом случае определяется наиболее предпочтительная альтернатива я(1. Ей присваивается максимальная оценка. Для всех остальных альтернатив эксперт указывает, во сколько раз они менее предпочтительны, чем а(1. Для корректировки численных оценок альтернатив можно использовать как стандартную процедуру метода Черчмена-Акоффа, так и попарное сравнение предпочтительности альтернатив. Если численные оценки альтернатив не совпадают с представлением эксперта об их предпочтительности, производится корректировка.
Метод фон Неймана—Моргенштерна. Он заключается в получении численных оценок альтернатив с помощью так называемых вероятностных смесей. В основе метода лежит предположение, согласно которому эксперт для любой альтернативы а-, менее предпочтительной, чем а(, но более предпочтительной, чем at, может указать число а (0 <р < \) такое, что альтернатива а, эквивалентна смешанной альтернативе (вероятностной смеси) [pat, (l-р) а/]. Смешанная альтернатива состоит в том, что альтернатива af выбирается с вероятностью Р, а альтернатива а{ с вероятностью \-Р. Очевидно, что если Р достаточно близко к 1, то альтернатива Oj менее предпочтительна, чем смешанная альтернатива [pat, (\-p)at]. В литературе помимо упомянутого выше предположения рассматривается система предположений (аксиом) о свойствах смешанных и несмешанных альтернатив. К числу таких предположений относятся предположение о связности и транзитивности отношения предпочтительности альтернатив, предположение о том, что смешанная альтернатива
х2р2 + ... + xNpN > Xj/j + х2р'2 + ... +xn p'N .
Таким образом, устанавливается существование функции полезности
xlPl+...+xNpN,
значение которой характеризует степень предпочтительности
любой смешанной альтернативы, в частности и несмешанной.
Более предпочтительна та смешанная альтернатива, для которой
значение функции полезности больше.
Рассмотренные выше методы экспертных оценок обладают
различными качествами, но приводят в общем случае к близким результатам. Практика применения этих методов показала, что наиболее эффективно комплексное применение различных методов для решения одной и той же задачи. Сравнительный анализ результатов повышает обоснованность делаемых выводов. При этом следует учитывать, что методом, требующим минимальных затрат, является ранжирование, а наиболее трудоемким метод последовательного сравнения (Черчмена Акоффа). Метод парного сравнения без дополнительной обработки не дает полного упорядочения объектов.
2.4.4. МЕТОДЫ ТИПА ДЕЛЬФИ
Название методов экспертной оценки типа Дельфи связано с древнегреческим городом Дельфи, где при храме Аполлона с IX в. до н.э. до IV в. н.э. по преданиям находился Дельфийский оракул.
126
Глава 2
Основы оценки сложных систем
127
3 отличие от традиционных методов экспертной оценки метод Дельфи предполагает полный отказ от коллективных обсуждений. Это делается для того, чтобы уменьшить влияние таких психологических факторов, как присоединение к мнению наиболее авторитетного специалиста, нежелание отказаться от публично выраженного мнения, следование за мнением большинства. В методе Дельфи прямые дебаты заменены программой последовательных индивидуальных опросов, проводимых в форме анкетирования. Ответы обобщаются и вместе с новой дополнительной информацией поступают в распоряжение экспертов, после чего они уточняют свои первоначальные ответы. Такая процедура повторяется несколько раз до достижения приемлемой сходимости совокупности высказанных мнений. Результаты эксперимента показали приемлемую сходимость оценок экспертов после пяти туров опроса.
Метод Дельфи первоначально был предложен О. Хелмером как итеративная процедура «мозговой атаки», которая должна помочь снизить влияние психологических факторов и повысить объективность результатов. Однако почти одновременно Дель-фи-процедуры стали основным средством повышения объективности экспертных опросов с использованием количественных оценок при оценке деревьев цели и при разработке сценариев за счет использования обратной связи, ознакомления экспертов с результатами предшествующего тура опроса и учета этих результатов при оценке значимости мнений экспертов.
Процедура Дельфи-метода заключается в следующем:
1) организуется последовательность циклов «мозговой атаки»;
2) разрабатывается
программа последовательных индивиду
альных опросов с помощью вопросников, исключающая контак
ты между
экспертами, но предусматривающая ознакомление их с
мнениями
друг друга между турами; вопросники от тура к туру
могут уточняться;
3) в наиболее развитых
методиках экспертам присваиваются
весовые коэффициенты значимости их мнений, вычисляемые на
основе
предшествующих опросов, уточняемые от тура к туру и
учитываемые
при получении обобщенных результатов оценок.
Первое практическое применение метода Дельфи к решению некоторых задач министерства обороны США, осуществленное RAND Corporation во второй половине 40-х гг., показало его эффективность и целесообразность распространения на широкий класс задач, связанный с оценкой будущих событий.
Недостатки метода Дельфи:
• значительный расход
времени на проведение экспертизы,
связанный с большим количеством последовательных повторе
ний
оценок;
• необходимость
неоднократного пересмотра экспертом сво
их
ответов, вызывающая у него отрицательную реакцию, что ска
зывается
на результатах экспертизы.
В 60-е гг. область практического применения метода Дельфи значительно расширилась, однако присущие ему ограничения привели к возникновению других методов, использующих экспертные оценки. Среди них особого внимания заслуживают методы QUEST, SEER, PATTERN.
Метод QUEST (Qualitative Utility Estimates for Science and Technology - количественные оценки полезности науки и техники) был разработан для целей повышения эффективности решений по распределению ресурсов, выделяемых на исследования и разработки. В основу метода положена идея распределения ресурсов на основе учета возможного вклада (определяемого метода экспертной оценки) различных отраслей и научных направлений в решение какого-либо круга задач.
Метод SEER (System for Event Evaluation and Review система оценок и обзора событий) предусматривает всего два тура оценки. В каждом туре привлекается различный состав экспертов. Эксперты первого тура - специалисты промышленности, эксперты второго тура - наиболее квалифицированные специалисты из органов, принимающих решения, и специалисты в области естественных и технических наук. Эксперт каждого тура не возвращается к рассмотрению своих ответов за исключением тех случаев, когда его ответ выпадает из некоторого интервала, в котором находится большинство оценок (например, интервала, в котором находится 90 % всех оценок).
2.4.5. МЕТОДЫ ТИПА ДЕРЕВА ЦЕЛЕЙ
Идея метода впервые была предложена Черчменом в связи с проблемами принятия решений в промышленности. Термин «дерево целей» подразумевает использование иерархической структуры, полученной путем разделения общей цели на подцели, а
128
Глава 2
Основы оценки сложных систем
129
их, в свою очередь, на более детальные составляющие (новые подцели, функции и т.д.)- Как правило, этот термин используется для структур, имеющих отношение строгого порядка, но метод дерева целей используется иногда и применительно к «слабым» иерархиям, в которых одна и та же вершина нижележащего уровня может быть одновременно подчинена двум или нескольким вершинам вышележащего уровня.
Разновидностью методов дерева целей и Дельфи является метод PA TTERN (Planning Assistance Through Technical Evaluation of Relevance Numbers помощь планированию посредством относительных показателей технической оценки), разработанный для повышения эффективности процессов принятия решений в области долгосрочной научно-технической ориентации крупной промышленной фирмы.
Сущность метода PATTERN заключается в следующем. Исходя из сформулированных целей потребителей продукции фирмы на прогнозируемый период осуществляется развертывание дерева целей. Для каждого уровня дерева целей вводится ряд критериев. С помощью экспертной оценки определяются веса критериев и коэффициенты значимости, характеризующие важность вклада целей в обеспечение критериев. Значимость некоторой цели определяется коэффициентом связи, представляющим сумму произведений всех критериев на соответствующие коэффициенты значимости. Общий коэффициент связи некоторой цели (относительно достижения цели высшего уровня) определяется путем перемножения соответствующих коэффициентов связи в направлении вершины дерева.
2.4.6. МОРФОЛОГИЧЕСКИЕ МЕТОДЫ
Основная идея морфологических методов систематически находить все мыслимые варианты решения проблемы или реализации системы путем комбинирования выделенных элементов или их признаков. В систематизированном виде морфологический подход разработан и применен впервые швейцарским астрономом Ф. Цвикки и долгое время был известен как метод Цвикки.
Цвикки предложил три метода морфологического исследования:
1. Метод
систематического покрытия поля (МСПП), основан
ный на выделении так
называемых опорных пунктов знания в
любой исследуемой области и использовании
для заполнения поля
некоторых сформулированных принципов
мышления.
2.
Метод
отрицания и конструирования (МОК), заключаю
щийся в
том, что на пути конструктивного прогресса стоят дог
мы и
компромиссные ограничения, которые есть смысл отрицать,
и
следовательно, сформулировав некоторые предложения, полез
но
заменить их затем на противоположные и использовать при
проведении
анализа.
3.
Метод
морфологического ящика (ММЯ), нашедший наи
более
широкое распространение. Идея ММЯ состоит в том, что
бы
определить все мыслимые параметры, от которых может за
висеть решение проблемы, представить их в виде матриц-строк,
а затем
определить в этом морфологическом матрице-ящике все
возможные
сочетания параметров по одному из каждой строки.
Полученные таким образом варианты могут снова подвергаться
оценке
и анализу в целях выбора наилучшего. Морфологический
ящик
может быть не только двумерным.
Построение и исследование по методу морфологического ящика проводится в пять этапов.
Этап 1. Точная формулировка поставленной проблемы.
Этап 2. Выделение показателей Pt, от которых зависит решение проблемы. По мнению Ф. Цвикки, при наличии точной формулировки проблемы выделение показателей происходит автоматически.
Этап 3. Сопоставление показателю Pf его значений ;? А и сведение этих значений в таблицу, которую Цвикки и называет морфологическим ящиком.
Набор значений различных показателей (по одному значению из каждой строки) представляет собой возможный вариант решения данной проблемы (например, вариант {р1,, р22, ... , pkn}, обозначенный на рис. 2.7). Такие наборы называются вариантами решения или просто вариантами. Общее число вариантов, содержащихся в морфологической таблице, равно N = К\К2 ... Кп, где Kt (i = 1, 2, ... , и) - число значений /-го показателя.
д—20
|
24 |
Глава 1
ского пространства обычно рассматривается временной интервал (0, °°).
Аксиома 2. Пространство состояний Z содержит не менее двух элементов. Эта аксиома отражает естественное представление о том, что сложная система может находиться в разных состояниях.
Аксиома 3. Система обладает свойством функциональной эмерджентности .
Эмерджентностъ (целостность) - это такое свойство системы S, которое принципиально не сводится к сумме свойств элементов, составляющих систему, и не выводится из них:
т
1
где yt - i-я характеристика системы S; т - общее количество характеристик.
При таком рассмотрении система является совокупностью моделей и, главное, отражает семантику предметной области в отличие от неинтерпретированных частных математических моделей. Другими словами, система - это совокупность взаимосвязанных элементов, обладающая интегративными свойствами (эмерджентностью), а также способ отображения реальных объектов.
В рамках изучаемой дисциплины под сложной кибернетической системой понимается реальный объект с управлением и его отображение в сознании исследователя как совокупность моделей, адекватная решаемой задаче.
123 КЛАССИФИКАЦИЯ СИСТЕМ
Системы принято подразделять на физические и абстрактные, динамические и статические, простые и сложные, естественные и искусственные, с управлением и без управления, непрерывные и дискретные, детерминированные и стохастические, открытые и замкнутые.
Основы системного анализа
Деление систем на физические и абстрактные позволяет различать реальные системы (объекты, явления, процессы) и системы, являющиеся определенными отображениями (моделями) реальных объектов.
Для реальной системы может быть построено множество систем - моделей, различаемых по цели моделирования, по требуемой степени детализации и по другим признакам.
Например, реальная ЛВС, с точки зрения системного администратора, - совокупность программного, математического, информационного, лингвистического, технического и других видов обеспечения, с точки зрения противника, - совокупность объектов, подлежащих разведке, подавлению (блокированию), уничтожению, с точки зрения технического обслуживания, - совокупность исправных и неисправных средств.
Деление систем на простые и сложные (большие) подчеркивает, что в системном анализе рассматриваются не любые, а именно сложные системы большого масштаба. При этом выделяют структурную и функциональную (вычислительную) сложность.
Общепризнанной границы, разделяющей простые, большие и сложные системы, нет. Однако условно будем считать, что сложные системы характеризуются тремя основными признаками: свойством робастности, наличием неоднородных связей и эмерджентностью.
Во-первых, сложные системы обладают свойством робастности - способностью сохранять частичную работоспособность (эффективность) при отказе отдельных элементов или подсистем. Оно объясняется функциональной избыточностью сложной системы и проявляется в изменении степени деградации выполняемых функций, зависящей от глубины возмущающих воздействий. Простая система может находиться не более чем в двух состояниях: полной работоспособности (исправном) и полного отказа (неисправном).
Во-вторых, в составе сложных систем кроме значительного количества элементов присутствуют многочисленные и разные по типу (неоднородные) связи между элементами. Основными типами считаются следующие виды связей: структурные (в том числе иерархические), функциональные, каузальные (причинно-следственные, отношения истинности), информационные, пространственно-временные. По этому признаку будем отличать сложные
|
26 |
Глава 1
системы от больших систем, представляющих совокупность однородных элементов, объединенных связью одного типа.
В-третьих, сложные системы обладают свойством, которое отсутствует у любой из составляющих ее частей. Это интегратив-ность (целостность), или эмерджентность. Другими словами, отдельное рассмотрение каждого элемента не дает полного представления о сложной системе в целом. Эмерджентность может достигаться за счет обратных связей, играющих важнейшую роль в управлении сложной системой.
Считается, что структурная сложность системы должна быть пропорциональна объему информации, необходимой для ее описания (снятия неопределенности). В этом случае общее количество информации о системе S, в которой априорная вероятность появленияу'-ro свойства равна р(у), определяется известным соотношением для количества информации
I(Y) = -Ip(yj)log2p(yj). (1.6)
Это энтропийный подход к дескриптивной (описательной) сложности.
Одним из способов описания такой сложности является оценка числа элементов, входящих в систему (переменных, состояний, компонентов), и разнообразия взаимозависимостей между ними.
В общей теории систем утверждается, что не существует систем обработки данных, которые могли бы обработать более чем 2-10547 бит в секунду на грамм своей массы. При этом компьютерная система, имеющая массу, равную массе Земли, за период, равный примерно возрасту Земли, может обработать порядка 10593 бит информации (предел Бреммермана). Задачи, требующие обработки более чем 10593 бит, называются трансвычислительными. В практическом плане это означает, что, например, полный анализ системы из 110 переменных, каждая из которых может принимать 7 разных значений, является трансвычислительной задачей.
Для оценки сложности функционирования систем применяется алгоритмический подход. Он основан на определении ресурсов (время счета или используемая память), используемых в системе при решении некоторого класса задач. Например, если функция времени вычислений является полиномиальной функцией от входных данных, то мы имеем дело с полиномиальным по вре-
Ф-
ч)
0
Ч
^
1с
Основы системного анализа
мени, или «легким» алгоритмом. В случае экспоненциального по времени алгоритма говорят о его «сложности». Алгоритмическая сложность изучается в теории NP-полных задач.
Сложные системы допустимо делить на искусственные и естественные (природные).
Искусственные системы, как правило, отличаются от природных наличием определенных целей функционирования (назначением) и наличием управления.
Рассмотрим еще один важный признак классификации систем. Принято считать, что система с управлением, имеющая нетривиальный входной сигнал x(t) и выходной сигнал y(t), может рассматриваться как преобразователь информации, перерабатывающий поток информации (исходные данные) x(t) в поток информации (решение по управлению) y(t).
В соответствии с типом значений x(t), y(t), z(t) и t системы делятся на дискретные и непрерывные.
Такое деление проводится в целях выбора математического аппарата моделирования. Так, теория обыкновенных дифференциальных уравнений и уравнений в частных производных позволяет исследовать динамические системы с непрерывной переменной (ДСНП). С другой стороны, современная техника создает антропогенные динамические системы с дискретными событиями (ДСДС), не поддающиеся такому описанию. Изменения состояния этих систем происходят не непрерывно, а в дискретные моменты времени, по принципу «от события к событию». Математические (аналитические) модели заменяются на имитационные, дискретно-событийные: модели массового обслуживания, сети Петри, цепи Маркова и др.
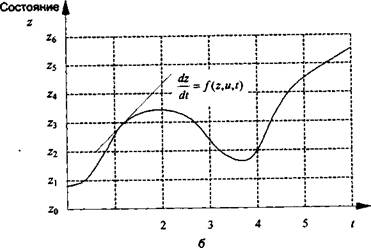
Примеры фазовых траекторий ДСДС и ДСНП показаны на рис. 1.3, а, б.
Для ДСДС траектория является кусочно-постоянной и формируется последовательностью событий и. Последовательность отрезков постоянства отражает последовательность состояний z системы, а длительность каждого отрезка отражает время пребывания системы в соответствующем состоянии. Под состоянием при этом понимается «физическое» состояние (например, число сообщений, ожидающих передачи в каждом узле обработки). Состояния принимают значения из дискретного множества.
28
Глава 1
Основы системного анализа
29
|
|
Состояние j,
z
| "3 |
|
25 24 23 |
| «5 |
| «2 |
F
|
t4 ts |
|
h '3 a |
| 0 1 |
to
Рис. 1.З. Типичные примеры фазовых траекторий ДСДС(а)иДСНП(б)
Таким образом, траектория описывается последовательностью из двух чисел (состояния и времени пребывания в нем). Следует подчеркнуть, что термин «дискретный» отличается от широко используемого прилагательного «цифровой», поскольку последнее означает лишь то, что анализ задачи ведется не в терминах вещественной числовой переменной, а численными методами. Траектория ДСНП, состояниями которой являются точки пространства R", постоянно изменяется и, вообще говоря, развивается на основе непрерывных входных воздействий. Здесь под состоянием понимается «математическое» состояние в том смысле, что оно включает в себя информацию к данному моменту времени (кроме внешних воздействий), которая необходима для однозначного определения дальнейшего поведения системы. Математическое определение включает в себя и физическое определение, но не наоборот.
Для перехода от детерминированной к стохастической системе достаточно в правые части соотношений (1.4) и (1.5) добавить в качестве аргументов функционалов случайную функцию p(t), принимающую значения на непрерывном или дискретном множестве действительных чисел.
Следует иметь в виду, что в отличие от математики для системного анализа, как и для кибернетики, характерен конструктивный подход к изучаемым объектам. Это требует обеспечения корректности задания системы, под которой понимается возможность фактического вычисления выходного сигнала y(t) (с той или иной степенью точности) для всех / > 0 при задании начального состояния системы z(0) и входного сигнала x(t) для всех it. Поэтому при изучении сложных систем приходится переходить к конечным аппроксимациям.
Системы с нетривиальным входным сигналом x(t), источником которого нельзя управлять (непосредственно наблюдать), или системы, в которых неоднозначность их реакции нельзя объяснить разницей в состояниях, называются открытыми.
Признаком, по которому можно определить открытую систему, служит наличие взаимодействия с внешней средой. Взаимодействие порождает проблему «предсказуемости» значений выходных сигналов и, как следствие, - трудности описания открытых систем.
| 30 |
Глава 1
Примером трудностей описания является понятие «странный аттрактор» - специфическое свойство некоторых сложных систем. Простейший аттрактор, называемый математиками неподвижной точкой, представляет собой такой вид равновесия, который характерен для состояния устойчивых систем после кратковременного возмущения (состояние покоя емкости с водой после встряхивания). Второй вид аттрактора - предельный цикл маятника. Все разновидности предельного цикла предсказуемы. Третья разновидность называется странным аттрактором. Обнаружено много систем, имеющих встроенные в них источники нарушений, которые не могут быть заранее предсказаны (погода, место остановки шарика в рулетке). В экспериментах наблюдали за краном, из которого нерегулярно капали капли, хотя промежутки должны быть регулярными и предсказуемыми, так как вентиль зафиксирован и поток воды постоянен.
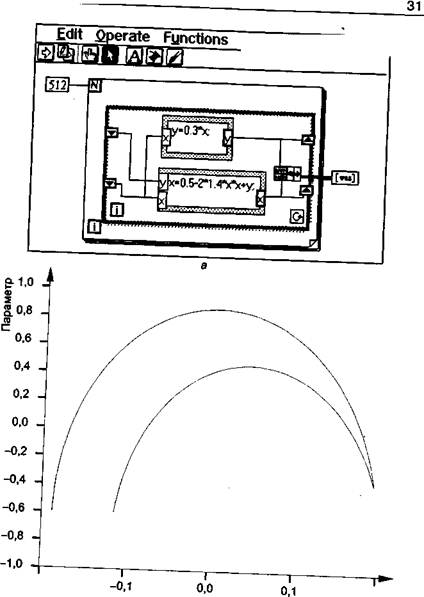
Математическим примером странного аттрактора является аттрактор Хенона - система уравнений, смоделированная в Lab VIEW (рис. 1.4, а, б).
Понятие открытости систем конкретизируется в каждой предметной области. Например, в области информатики открытыми информационными системами называются программно-аппаратные комплексы, которым присущи следующие свойства:
• переносимость
(мобильность) - программное обеспечение
(ПО)
может быть легко перенесено на различные аппаратные
платформы
и в различные операционные среды;
• стандартность - программное обеспечение
соответствует
опубликованному
стандарту независимо от конкретного разра
ботчика ПО;
• наращиваемость
возможностей - включение новых про
граммных
и технических средств, не предусмотренных в перво
начальном
варианте;
• совместимость - возможность взаимодействовать
с други
ми
комплексами на основе развитых интерфейсов для обмена
данными
с прикладными задачами в других системах.
Примером открытой среды является модель OSE (Open System Environment), предложенная комитетом IEEE POSIX. На основе этой модели Национальный институт стандартов и технологии США выпустил документ «Application Portability Profile (APP). The U.S. Government's Open System Environment Profile OSE/1
|
Windows Iext He'P |
| -0,2 |
Основы системного анализа
0,2 Состояние
рис. 1.4. Аттрактор Хенона: - программная модель; б - поведение в пространстве состояний
32
Глава 1
Основы системного анализа
33
Version 2.0», который определяет рекомендуемые спецификации в области информационных технологий, гарантирующие мобильность системного и прикладного программного обеспечения.
В отличие от открытых замкнутые (закрытые) системы изолированы от среды - не оставляют свободных входных компонентов ни у одного из своих элементов. Все реакции замкнутой системы однозначно объясняются изменением ее состояний. Вектор входного сигнала x(t) в замкнутых системах имеет нулевое число компонентов и не может нести никакой информации. Замкнутые системы в строгом смысле слова не должны иметь не только входа, но и выхода. Однако даже в этом случае их можно интерпретировать как генераторы информации, рассматривая изменение их внутреннего состояния во времени. Примером физической замкнутой системы является локальная сеть для обработки конфиденциальной информации.
Основным противоречием, которое приходится разрешать в замкнутых системах, является проблема возрастания энтропии. Согласно второму закону термодинамики по мере движения замкнутой системы к состоянию равновесия она стремится к максимальной энтропии (дезорганизации), соответствующей минимальной информации. Открытые системы могут изменить это стремление к максимальной энтропии, получая внешнюю по отношению к системе свободную энергию, и этим поддерживают организацию.
закон функционирования Fs, и в зависимости от целей моделирования входной сигнал x(t) может быть разделен на три подмножества:
• неуправляемых входных
сигналов xt е X, I = 1, ... , kx, пре
образуемых
рассматриваемым элементом;
• воздействий внешней
среды «v e N, v = 1, ... , kn, представ
ляющих
шум, помехи;
• управляющих сигналов (событий) ит е U, т = 1....... ku,
появление которых приводит к переводу элемента из одного состояния в другое.
Иными словами, элемент - это неделимая наименьшая функциональная часть исследуемой системы, включающая < х, п, и, у, f^> и представляемая как «черный ящик» (рис. 1.5). Функциональную модель элемента будем представлять как y(t) = Fs(x, п, и, t).
Входные сигналы, воздействия внешней среды и управляющие сигналы являются независимыми переменными. При строгом подходе изменение любой из независимых переменных влечет за собой изменение состояния элемента системы. Поэтому в дальнейшем будем обобщенно обозначать эти сигналы как x(t), a функциональную модель элемента - как y(t) = Fs(x(t)), если это не затрудняет анализ системы.
Выходной сигнал y(t), в свою очередь, представляют совокупностью характеристик элемента j>. e Y,j = l,...,k
1.2.4.
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ СИСТЕМНОГО АНАЛИЗА
Для оперирования основными понятиями системного анализа будем придерживаться следующих словесно-интуитивных или формальных определений.
Элемент - некоторый объект (материальный, энергетический, информационный), обладающий рядом важных свойств и реализующий в системе определенный закон функционирования F8, внутренняя структура которого не рассматривается.
Формальное описание элемента системы совпадает с описанием подмодели Ч* . Однако функционалы g и / заменяются на
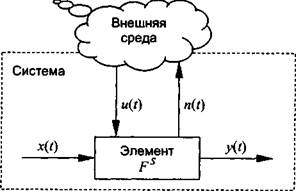
Рис. 1.5. Элемент системы как «черный ящик»
3-20
34
Глава 1
Основы системного анализа
35
Под средой понимается множество объектов S 'вне данного элемента (системы), которые оказывают влияние на элемент (систему) и сами находятся под воздействием элемента (системы),
Правильное разграничение исследуемого реального объекта и среды является необходимым этапом системного анализа. Часто в системном анализе выделяют понятие «суперсистема» - часть внешней среды, для которой исследуемая система является элементом.
Подсистема - часть системы, выделенная по определенному признаку, обладающая некоторой самостоятельностью и допускающая разложение на элементы в рамках данного рассмотрения.
Система может быть разделена на элементы не сразу, а последовательным расчленением на подсистемы - совокупности элементов. Такое расчленение, как правило, производится на основе определения независимой функции, выполняемой данной совокупностью элементов совместно для достижения некой частной цели, обеспечивающей достижение общей цели системы. Подсистема отличается от простой группы элементов, для которой не выполняется условие целостности.
Последовательное разбиение системы в глубину приводит к иерархии подсистем, нижним уровнем которых является элемент. Типичным примером такого разбиения является структура Паскаль-программы. Так, например, тело основной программы включает модули - подсистемы первого уровня, модули включают функции и процедуры - подсистемы второго уровня, функции и процедуры включают операнды и операторы - элементы системы.
Характеристика -то, что отражает некоторое свойство элемента системы.
Характеристика v задается кортежем ^. = < name, {value} >, где пате - имя 7-й характеристики, {value} - область допустимых значений. Область допустимых значений задается перечислением этих значений или функционально, с помощью правил вычисления (измерения) и оценки.
Характеристики делятся на количественные и качественные в зависимости от типа отношений на множестве их значений.
Если на множестве значений заданы метризованные отношения, когда указывается не только факт выполнения отношения p(W, у?), н° также и степень количественного превосходства, то
характеристика является количественной. Например, размер экрана (см), максимальное разрешение (пиксель) являются количественными характеристиками мониторов, поскольку существуют шкалы измерений этих характеристик в сантиметрах и пикселях соответственно, допускающие упорядочение возможных значений по степени количественного превосходства: размер экрана монитора у! больше, чем размер экрана монитора _у А на 3 см (аддитивное метризованное отношение) или максимальное разрешение у/1 выше, чем максимальное разрешение у?,в два раза (мультипликативное метризованное отношение).
Если пространство значений не метрическое, то характеристика называется качественной. Например, такая характеристика монитора, как комфортное разрешение, хотя и измеряется в пикселях, является качественной. Поскольку на комфортность влияют мерцание, нерезкость, индивидуальные особенности пользователя и т.д., единственным отношением на шкале комфортности является отношение эквивалентности, позволяющее различить мониторы как комфортные и некомфортные без установления количественных предпочтений.
Количественная характеристика называется параметром.
Часто в литературе понятия «параметр» и «характеристика» отождествляются на том основании, что все можно измерить. Но в общем случае полезно разделять параметры и качественные характеристики, так как не всегда возможно или целесообразно разрабатывать процедуру количественной оценки какого-либо свойства.
Характеристики элемента являются зависимыми переменными и отражают свойства элемента. Под свойством понимают сторону объекта, обусловливающую его отличие от других объектов или сходство с ними и проявляющуюся при взаимодействии с другими объектами.
Свойства задаются с использованием отношений одного из основных математических понятий, используемых при анализе и обработке информации. На языке отношений единым образом можно описать воздействия, свойства объектов и связи между ними, задаваемые различными признаками. Существует несколько форм представления отношений: функциональная (в виде функции, функционала, оператора), матричная, табличная, логическая, графовая, представление сечениями, алгоритмическая (в виде словесного правила соответствия).
з-
36
Глава 1
Основы системного анализа
37
Свойства классифицируют на внешние, проявляющиеся в форме выходных характеристик yt только при взаимодействии с внешними объектами, и внутренние, проявляющиеся в форме переменных состояния z, при взаимодействии с внутренними элементами рассматриваемой системы и являющиеся причиной внешних свойств.
Одна из основных целей системного анализа - выявление внутренних свойств системы, определяющих ее поведение.
По структуре свойства делят на простые и сложные (интегральные). Внешние простые свойства доступны непосредственному наблюдению, внутренние свойства конструируются в нашем сознании логически и не доступны наблюдению.
Следует помнить о том, что свойства проявляются только при взаимодействии с другими объектами или элементами одного объекта между собой.
По степени подробности отражения свойств выделяют горизонтальные (иерархические) уровни анализа системы. По характеру отражаемых свойств выделяют вертикальные уровни анализа - аспекты. Этот механизм лежит в основе утверждения о том, что для одной реальной системы можно построить множество абстрактных систем.
При проведении системного анализа на результаты влияет фактор времени. Для своевременного окончания работы необходимо правильно определить уровни и аспекты проводимого исследования. При этом производится выделение существенных для данного исследования свойств путем абстрагирования от несущественных по отношению к цели анализа подробностей.
Формально свойства могут быть представлены также и в виде закона функционирования элемента.
Законом функционирования Fs, описывающим процесс функционирования элемента системы во времени, называется зависимость y(t) = Fs( x, n, и, t).
Оператор Fs преобразует независимые переменные в зависимые и отражает поведение элемента (системы) во времени - процесс изменения состояния элемента (системы), оцениваемый по степени достижения цели его функционирования. Понятие поведения принято относить только к целенаправленным системам и оценивать по показателям.
Цель - ситуация или область ситуаций, которая должна быть достигнута при функционировании системы за определенный промежуток времени. Цель может задаваться требованиями к показателям результативности, ресурсоемкости, оперативности функционирования системы либо к траектории достижения заданного результата. Как правило, цель для системы определяется старшей системой, а именно той, в которой рассматриваемая система является элементом.
Показатель - характеристика, отражающая качествоу'-й системы или целевую направленность процесса (операции), реализуемого у'-й системой:
YJ = WJ(n, x, и).
Показатели делятся на частные показатели качества (или эффективности) системы у>(, которые отражают /-е существенное свойство7-й системы, и обобщенный показатель качества (или эффективности) системы Y J — вектор, содержащий совокупность свойств системы в целом. Различие между показателями качества и эффективности состоит в том, что показатель эффективности характеризует процесс (алгоритм) и эффект от функционирования системы, а показатели качества - пригодность системы для использования ее по назначению.
Вид отношений между элементами, который проявляется как некоторый обмен (взаимодействие), называется связью. Как правило, в исследованиях выделяются внутренние и внешние связи. Внешние связи системы - это ее связи со средой. Они проявляются в виде характерных свойств системы. Определение внешних связей позволяет отделить систему от окружающего мира и является необходимым начальным этапом исследования.
В ряде случаев считается достаточным исследование всей системы ограничить установлением ее закона функционирования. При этом систему отождествляют с оператором F5 и представляют в виде «черного ящика». Однако в задачах анализа обычно требуется выяснить, какими внутренними связями обусловливаются интересующие исследователя свойства системы. Поэтому основным содержанием системного анализа является определение структурных, функциональных, каузальных, информационных и пространственно-временных внутренних связей системы.
38
Глава 1
Основы системного анализа
39
Структурные связи обычно подразделяют на иерархические, сетевые, древовидные и задают в графовой или матричной форме.
Функциональные и пространственно-временные связи задают как функции, функционалы и операторы.
Каузальные (причинно-следственные) связи описывают на языке формальной логики.
Для описания информационных связей разрабатываются ин-фологические модели.
Выделение связей разных видов наряду с выделением элементов является существенным этапом системного анализа и позволяет судить о сложности рассматриваемой системы.
Важным для описания и исследования систем является понятие алгоритм функционирования As, под которым понимается метод получения выходных характеристик y(t) с учетом входных воздействий x(i), управляющих воздействий u(f) и воздействий внешней среды n(t).
По сути, алгоритм функционирования раскрывает механизм проявления внутренних свойств системы, определяющих ее поведение в соответствии с законом функционирования. Один и тот же закон функционирования элемента системы может быть реализован различными способами, т. е. с помощью множества различных алгоритмов функционирования As.
Наличие выбора алгоритмов As приводит к тому, что системы с одним и тем же законом функционирования обладают разным качеством и эффективностью процесса функционирования.
Качество - совокупность существенных свойств объекта, обусловливающих его пригодность для использования по назначению. Оценка качества может производиться по одному интегральному свойству, выражаемому через обобщенный показатель качества системы.
Процессом называется совокупность состояний системы z(/0), z(/,), ... , z(tk), упорядоченных по изменению какого-либо параметра г, определяющего свойства системы.
Формально процесс функционирования как последовательная смена состояний интерпретируется как координаты точки в А>мерном фазовом пространстве. Причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний {z} называется пространством состояний системы.
Проиллюстрировать понятие процесса можно на следующем примере. Состояние узла связи будем характеризовать количеством исправных связей на коммутаторе. Сделаем ряд измерений, при которых количество связей будет иметь разные значения. Будет ли полученный набор значений характеризовать некоторый процесс? Без дополнительной информации это неизвестно. Если это упорядоченные по времени / (параметр процесса) значения, то - да. Если же значения перемешаны, то соответствующий набор состояний не будет процессом.
В общем случае время в модели системы S может рассматриваться на интервале моделирования (О, 7) как непрерывное, так и дискретное, т.е. квантованное на отрезки длиной Д/ временных единиц каждый, когда T = mAt, где т - число интервалов дискретизации.
Эффективность процесса - степень его приспособленности к достижению цели.
Принято различать эффективность процесса, реализуемого системой, и качество системы. Эффективность проявляется только при функционировании и зависит от свойств самой системы, способа ее применения и от воздействий внешней среды.
К? и т ерий эффективности - обобщенный показатель и правило выбора лучшей системы (лучшего решения). Например, Y* = max{YJ}.
Если решение выбирается по качественным характеристикам, то критерий называется решающим правилом.
Если нас интересует не только закон функционирования, но и алгоритм реализации этого закона, то элемент не может быть представлен в виде «черного ящика» и должен рассматриваться как подсистема (агрегат, домен) - часть системы, выделенная по функциональному или какому-либо другому признаку.
Описание подсистемы в целом совпадает с описанием элемента. Но для ее описания дополнительно вводится понятие множества внутренних (собственных) характеристик подсистемы А,е Н, 1=1, ..., kh.
Оператор Fs преобразуется к виду y(t) = Fs ( х, п, и, h, t), a метод получения выходных характеристик кроме входных воздействий x(t), управляющих воздействий u(t) и воздействий внешней среды n(f) должен учитывать и собственные характеристики подсистемы h(t).
40
Глава 1
Основы системного анализа
41
Описание закона функционирования системы наряду с аналитическим, графическим, табличным и другими способами в ряде случаев может быть получено через состояние системы. Состояние системы - это множество значений характеристик системы в данный момент времени.
Формально состояние системы в момент времени Г0 < t* < Т полностью определяется начальным состоянием z(/0), входными воздействиями x(t), управляющими воздействиями u(i), внутренними параметрами h(t) и воздействиями внешней среды n(i), которые имели место за промежуток времени t* - tQ, с помощью глобальных уравнений динамической системы (1.4), (1.5), преобразованных к виду
Вход системы А
Вход системы "В
| 0. |
g, t];
y(t) = g(z(t), t).
Здесь уравнение состояния по начальному состоянию z(f0) и переменным х, и, п, h определяет вектор-функцию z(i), а уравнение наблюдения по полученному значению состояний z(t) определяет переменные на выходе подсистемы y(t).
Таким образом, цепочка уравнений объекта «вход-состояния-выход» позволяет определить характеристики подсистемы:
ХО =/Ш'0)' х, и, п, h, 0]
и под математической моделью реальной системы можно понимать конечное подмножество переменных (x(t), u(t), n(i), h(t)} вместе с математическими связями между ними и характеристиками y(f).
Структура - совокупность образующих систему элементов и связей между ними. Это понятие вводится для описания подмодели Ч*6. В структуре системы существенную роль играют связи. Так, изменяя связи при сохранении элементов, можно получить другую систему, обладающую новыми свойствами или реализующую другой закон функционирования. Это наглядно видно на рис. 1 .6, если в качестве системы рассматривать соединение трех проводников, обладающих разными сопротивлениями.
Необходимость одновременного и взаимоувязанного рассмотрения состояний системы и среды требует определения понятий «ситуация» и «проблема».
|
Выход системы А a |
Выход системы В б
Рис. 1.6. Роль связей в структуре системы: а - параллельная связь; б - последовательная связь
Ситуация - совокупность состояний системы и среды в один и тот же момент времени.
Проблема - несоответствие между существующим и требуемым (целевым) состоянием системы при данном состоянии среды в рассматриваемый момент времени.
1.3. МОДЕЛИ СЛОЖНЫХ СИСТЕМ
Под моделированием понимается процесс исследования реальной системы, включающий построение модели, изучение ее свойств и перенос полученных сведений на моделируемую систему.
Общими функциями моделирования являются описание, объяснение и прогнозирование поведения реальной системы.
Типовыми целями моделирования могут быть поиск оптимальных или близких к оптимальным решений, оценка эффективности решений, определение свойств системы (чувствительности
42
Глава 1
Основы системного анализа
43
к изменению значений характеристик и др.), установление взаимосвязей между характеристиками системы, перенос информации во времени. Термин «модель» имеет весьма многочисленные трактовки. В наиболее общей формулировке мы будем придерживаться следующего определения модели. Модель - это объект, который имеет сходство в некоторых отношениях с прототипом и служит средством описания и/или объяснения, и/или прогнозирования поведения прототипа.
Формальное определение модели (1.1) определяет модель как изоморфизм А на Ч1.
Частные модели могут обозначаться как гомоморфизм:
Оператор / в этом обозначении указывает на способ, который позволяет построить требуемую модель.
Важнейшим качеством модели является то, что она дает упрощенный образ, отражающий не все свойства прототипа, а только те, которые существенны для исследования.
Сложные системы характеризуются выполняемыми процессами (функциями), структурой и поведением во времени. Для адекватного моделирования этих аспектов в автоматизированных информационных системах различают функциональные, информационные и поведенческие модели, пересекающиеся друг с другом.
Функциональная модель системы описывает совокупность выполняемых системой функций, характеризует морфологию системы (ее построение) - состав функциональных подсистем, их взаимосвязи.
Информационная модель отражает отношения между элементами системы в виде структур данных (состав и взаимосвязи).
Поведенческая (событийная) модель описывает информационные процессы (динамику функционирования), в ней фигурируют такие категории, как состояние системы, событие, переход из одного состояния в другое, условия перехода, последовательность событий.
Особенно велико значение моделирования в системах, где натурные эксперименты невозможны по целому ряду причин: сложность, большие материальные затраты, уникальность, дли-
тельность эксперимента. Так, нельзя «провести войну в мирное время», натурные испытания некоторых типов систем связаны с их разрушением, для экспериментальной проверки сложных систем управления требуется длительное время и т.д.
Можно выделить три основные области применения моделей: обучение, научные исследования, управление. При обучении с помощью моделей достигается высокая наглядность отображения различных объектов и облегчается передача знаний о них. Это в основном модели, позволяющие описать и объяснить систему. В научных исследованиях модели служат средством получения, фиксирования и упорядочения новой информации, обеспечивая развитие теории и практики. В управлении модели используются для обоснования решений. Такие модели должны обеспечить как описание, так и объяснение и предсказание поведения систем.
1.3.1.
КЛАССИФИКАЦИЯ ВИДОВ МОДЕЛИРОВАНИЯ СИСТЕМ
Классификация видов моделирования может быть проведена по разным основаниям. Один из вариантов классификации приведен на рис. 1.7.
В соответствии с классификационным признаком полноты моделирование делится на полное, неполное и приближенное. При полном моделировании модели идентичны объекту во времени и пространстве. Для неполного моделирования эта идентичность не сохраняется. В основе приближенного моделирования лежит подобие, при котором некоторые стороны реального объекта не моделируются совсем. Теория подобия утверждает, что абсолютное подобие возможно лишь при замене одного объекта другим точно таким же. Поэтому при моделировании абсолютное подобие не имеет места. Исследователи стремятся к тому, чтобы модель хорошо отображала только исследуемый аспект системы. Например, для оценки помехоустойчивости дискретных каналов передачи информации функциональная и информационная модели системы могут не разрабатываться. Для достижения цели моделирования вполне достаточна событийная
|
Общегосударственные органы управления |
|
Республиканские и отраслевые органы управления |
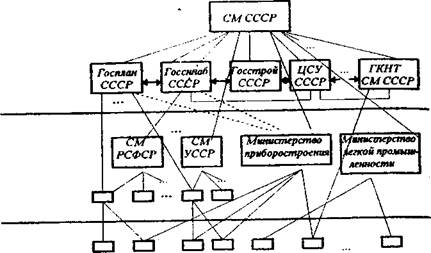 Разумеется, на _>ис. 1.15
иллкктрщкжаи только общий принцип взаимоотноше
Разумеется, на _>ис. 1.15
иллкктрщкжаи только общий принцип взаимоотноше
ний между
различными оргацамн управления страной, а реальная структ ра форми
руется с
помощью соответствующих нормативно-правовых и иорматиЕ к»-мстоди-
чсских документов, в которых регламентируются конкретные взаимодействия между
органами
управления. *
Предприятия и организации
Рис. 1.15
Смешанный характер носит и организационная структура
современно
го предприятия
(объединения, акционерного общества и т. п.)- Как будет
показано в гл. 5, линейный принцип управления
реализуется в оргструкту
рах с помощью древовидных иерархических
структур, линейно-фунж-
цлональные оргструктуры представляют собой иерархию со "слабыми*
связями, программно-целевые структуры
основаны на приоритете горизон
тальных связей, матричные (тензорные) - на равноправии составляющих
многомерной организационной структуры. /
Оргструктуры, называемые матричными, являются фактически тоже смешанными, поскольку они сочетают матричные и иерархические представления.
Структуры с произвольными связями. Этот вид структур обыч-, но используется на начальном этапе познания объекта, новой про?, блемы, когда идет поиск способов установления взаимоотношений, между перечисляемыми компонентами, нет ясности в характере^ связей между элементами, и не могут быть определены не только последовательности их взаимодействия во времени (сетевые модели), но и распределение элементов по уровням иерархии.
При этом важно обратить внимание на достаточно распространенную ошибку при применении произвольных структур. В связи с/ 44
>еяс:кхггью взаимодействий между элементами вначале стремятся установить и представить графически все связи (рис. 1.16 а). Однако гагие представление не добавляет ничего нового к представлению элементов без связей (рис. 1.16 б), поскольку принятие решений
вязано всегда с установлением наиболее существенных связей для
.ринятия решения.
Представление типа а) I 1
| п |
и« 1.16 а правомерно //\
 ех случаях, когда
ех случаях, когда
от 1 бы устанавливает-
| ] П |
|
Рис. 1.16 |
л :нла связей, их на-:фг. вленность. В приве-декном же виде это представление аналогично квадрату К.Малевича, который каждый может воспринимать по-своему.
Следует отметить, что приведенные на рис. 1.16 представления фактически являются различными подходами к исследованию проблемы: можно не имея вначале ни одной связи, искать и оценивать их последовательно, используя, например, один ;п методов морфологического моделирования - метод систематического покрытия г?оля (см. гл. 2), или другие методы анализа пространства состояний путем введения тех или иных мер близости; а можно действовать по принципу Родена, сформулированному в стихотворной форме Николаем Дориэо: "Взяли камень, убрали из камня все лишнее, и остались прелестные эти черты." '
Формируются структуры с произвольными связями путем установления возможных отношений между предварительно выделенными элементами системы, введения ориентировочных оценок силы связей, и, как правило, после предварительного формирования и анализа таких структур связи упорядочивают и получают иерархические или сетевые структуры.
1.4. Ююссяфякацяк скстем
Примеры классификаций систем. Системы разделяют на классы по различным признакам, и в зависимости от решаемой задачи можно выбирать разные принципы классификации.
Предпринимались попытки классифицировать системы по виду отображаемого объекта (технические, биологические, экономические и т. п. системы); по виду научного направления, используемого для их моделирования (математические, физические, химические и др.). Системы делят на детерминированные и стохастические; открытые и закрытые; абстрактные и материальные (существующие в объективной реальности) и т. д.
Н.Доризо. У статуи Венеры. — В сб.: Избранное. — М.: Гос. худ. лит., 1965. — С. 9.
45
Моделирование систем
J_
Полное Неполное Приближенное
Детерминированное Стохастическое
Статическое Динамическое
I
Дискретное Дискретно-непрерывное Непрерывное
I ,
I
| Наглядное: • гипотетическое; • аналоговое; • макетирование | Символическое: • языковое; • знаковое | Математическое: • аналитическое; • имитационное; • комбинированное; • информационное; • структурное; • ситуационное | Натурное: • научный эксперимент; • комплексные испытания; • производственный эксперимент | Физическое: • в реальном времени; • в модельном времени |
Рис. 1.7. Классификация видов моделирования
ш
ш ш
| на применении аналогий различных уровней. Для достаточно простых объектов наивысшим уровнем является полная аналогия. С усложнением системы используются аналогии последую- |
|те, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Этот вид моделирования используется, когда знаний об объекте недостаточно для построения формальных моделей. Аналоговое моделирование основывается |
| потеза о закономерностях протекания процесса в реальном объек- |
| В основу гипотетического моделирования закладывается ги- |
1века о реальных объектах создаются наглядные модели, отображающие явления и процессы, протекающие в объекте. Примером таких моделей являются учебные плакаты, рисунки, схемы, диаграммы. |
| При наглядном моделировании на базе представлений чело- |
В зависимости от типа носителя и сигнатуры модели различаются следующие виды моделирования: детерминированное и стохастическое, статическое и динамическое, дискретное, непрерывное и дискретно-непрерывное. Детерминированное моделирование отображает процессы, в которых предполагается отсутствие случайных воздействий. Стохастическое моделирование учитывает вероятностные процессы и события. Статическое моделирование служит для описания состояния объекта в фиксированный момент времени, а динамическое - для исследования объекта во времени. При этом оперируют аналоговыми (непрерывными), дискретными и смешанными моделями. В зависимости от формы реализации носителя и сигнатуры моделирование классифицируется на мысленное и реальное. Мысленное моделирование применяется тогда, когда модели не реализуемы в заданном интервале времени либо отсутствуют условия для их физического создания (например, ситуация микромира). Мысленное моделирование реальных систем реализуется в виде наглядного, символического и математического. Для представления функциональных, информационных и событийных моделей этого вида моделирования разработано значительное количество средств и методов. |
1 модель, описываемая матрицей условных вероятностей \\pf\\ переходов г-го символа алфавита в 7-й. ч |
О о \ Z о о 3 о з 0) 1 ы 0> £>. СЛ |
Классификации всегда относительны. Так, в детерминированной системе можно найти а ементы стохастичности. и. напротив, детерминированную систему можно считать часп.ым случаем стохастической (при вероятности равной единице^. Аналогично, если принять во внимание диалектику субъективно о и объективного в системе, то станет понятной относительность >азделения системы на абстрактные и объективно существующие: то могут быть стадии развития одной и той же системы.
Действительно, естсствсшше и искусственные объект J, < гражаясь в сознании человека, выступают в {юли абстракций, понятий, я абстр ten ые проекты создаваемых систем воплощаются в реально существующие объск ы, чоторие можно ощу-Tim,, а при изучении снова отразтъ в виде абстрактной сис"^ем j.
Однако относительность классификаций не должна останавливать исследователей. Цель любой классификации - ограничить выбор подходов к отображению системы, сопоставить выделенным классам приемы и методы системного анализа и дать рекомендации по выбору методов для соответствующего класса систем. При этом система, в принципе, может быть одновременно охарактеризована несколькими признаками, т. е. ей может быть найдено место одновременно в разных классификациях, каждая из которых может оказаться полезной при выборе методов моделирования.
Рассмотрим для примера некоторые из наиболее важных классификаций систем.
Открытые и закрытые системы. Понятие открытой системы ввел Л. фон Берталанфи [1.6]. Основные отличительные черты открытых систем - способность обмениваться со средой массой, энергией и информацией. В отличие от них закрытые или замкнутые системы предполагаются (разумеется, с точностью до принятой чувствительности модели) полностью лишенными этой способности, т. е. изолированными от среды.
Возможны частные случаи: например, не учитываются гравитационные и энергетические процессы, а отражается в модели системы только обмен информацией со средой; тогда говорят об информационно-проницаемых или соответственно об информационно-непроницаемых системах.
С моделью открытой системы Берталанфи можно познакомиться в [1.6, 1.7, 1.62]. Там же рассматриваются некоторые интересные особенности открытых систем. Одна из наиболее важных состоит в следующем. В открытых системах "проявляются термодинамические закономерности, которые кажутся парадоксальными и противоречат второму началу термодинамики" ([1.7], с. 42). Напомним, что второй закон термодинамики ("второе начало"), сформулированный для закрытых систем, характеризует систему' ростом энтротга, стремлением к неупорядоченности, разрушению.
Проявляется этот закон и в открытых системах (например, старение биологических систем). Однако в отличие от закрытых в от-
46
системах возможен "а вод эттюпии", ее снижение; "по-системы могут сохранять свой высокий уровень и даже раз-<;шаться в сторону увеличения порядка сложности" ([1.7], с. 42), т. е. них проявляется рассматриваемая в следующем разделе законо-мсрность самооргшшзации (хотя Берталанфи этот термин еще не использовал). Именно поэтому важно для системы управления поддерживать хороший обмен информацией со средой.
Целенаправленные, целеустремленные с и с-
г е м ы. Как уже отмечалось, не всегда при изучении систем можно
применять понятие цель. Однако при изучении экономических, ор-
анизационных объектов важно выделять класс целенаправленных
;ши целеустремленных систем [13, 4.1].
В этом классе, в свою очередь, можно выделить системы, в которых цели задаются извне (обычно это имеет место в закрытых системах), и системы, в которых цели формируются внутри системы (что характерно для открытых, самоорганизующихся систем).
Закономерности целеобразоваяия в самоорганизующихся системах рассматриваются ниже. Методики, помогающие формировать и анализировать структуры целей, характеризуются в гл. 4.
Классяфккацшв актам» га» слсжностн. Существует несколько подходов к разделению систем по сложности. Так, Г-Н.Поваров связывает сложность с размерами системы [1.34].
В то же время существует точка зрения, что большие (по величине, количеству элементов) и сложные (по сложности связей, алгоритмов поведения) системы — это разные классы систем [13].
Б.С.Флейшман за основу классификации принимает сложность поведения системы [1.52].
Одна из наиболее полных и интересных классификаций по уровням сложности предложена К.Боулдишом [1ЛО, 1.63]. Выделенные в ней уровни приведены в табл. 1.1.
В классификации К.Бсулдинга каждый последующий класс включает в себя предыдущий, характеризуется большим проявлением свойств открытости и стохастичности поведения, более ярко выраженными проявлениями закономерностей иерархичности и историчности (рассматриваемых ниже), хотя это не всегда отмечается, а также более сложными "механизмами" функционирования и развития.
Оценивая классификации с точки зрения их использования при выборе методов моделирования систем, следует отметить, что такие рекомендации (вплоть до выбора математических методов) имеются в них только для классов относительно низкой сложности (в классификации К.Боулдинга, например, - для уровня неживых систем),
47
46
Глава 1
Основы системного анализа
47
щих уровней, когда аналоговая модель отображает несколько (или только одну) сторон функционирования объекта. Макетирование применяется, когда протекающие в реальном объекте процессы не поддаются физическому моделированию или могут предшествовать проведению других видов моделирования. В основе построения мысленных макетов также лежат аналогии, обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте.
Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает его основные свойства с помощью определенной системы знаков и символов. В основе языкового моделирования лежит некоторый тезаурус, который образуется из набора понятий исследуемой предметной области, причем этот набор должен быть фиксированным. Под тезаурусом понимается словарь, отражающий связи между словами или иными элементами данного языка, предназначенный для поиска слов по их смыслу.
Традиционный тезаурус состоит из двух частей: списка слов и устойчивых словосочетаний, сгруппированных по смысловым (тематическим) рубрикам; алфавитного словаря ключевых слов, задающих классы условной эквивалентности, указателя отношений между ключевыми словами, где для каждого слова указаны соответствующие рубрики. Такое построение позволяет определить семантические (смысловые) отношения иерархического (род/вид) и неиерархического (синонимия, антонимия, ассоциации) типа.
Формально тезаурусом называют конечное непустое множество V слов v, отвечающее следующим условиям:
1)
имеется
непустое подмножество У0 с V, называемое мно
жеством дескрипторов;
2)
имеется
симметричное, транзитивное, рефлексивное отно
шение R с Fx V, такое, что:
б) V] е V \ vq => (3v е V0)(vR Vl) •
при этом отношение R называется синонимическим, а слова v,, v2, отвечающие этому отношению, называются синонимическими дескрипторами;
3) имеется транзитивное и несимметричное отношение К с: vqx.vq, называемое обобщающим отношением.
В случае если два дескриптора v( и v2 удовлетворяют отношению v, К v2, то полагают, что дескриптор v, более общий, чем дескриптор v2.
Элементы множества У\У0 называются множеством аскрип-торов.
Между тезаурусом и обычным словарем имеются принципиальные различия. Тезаурус - словарь, который очищен от неоднозначности, т.е. в нем каждому слову может соответствовать лишь единственное понятие, хотя в обычном словаре одному слову может соответствовать несколько понятий.
Если ввести условное обозначение отдельных понятий, т.е. знаки, а также определенные операции между этими знаками, то можно реализовать знаковое моделирование и с помощью знаков отображать набор понятий - составлять отдельные цепочки из слов и предложений. Используя операции объединения, пересечения и дополнения теории множеств, можно в отдельных символах дать описание какого-то реального объекта.
Математическое моделирование - это процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью. В принципе, для исследования характеристик любой системы математическими методами, включая и машинные, должна быть обязательно проведена формализация этого процесса, т.е. построена математическая модель. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, от требуемой достоверности и точности решения задачи. Любая математическая модель, как и всякая другая, описывает реальный объект с некоторой степенью приближения.
Для представления математических моделей могут использоваться различные формы записи. Основными являются инвариантная, аналитическая, алгоритмическая и схемная (графическая).
Инвариантная форма - запись соотношений модели с помощью традиционного математического языка безотносительно к методу решения уравнений модели. В этом случае модель может быть представлена как совокупность входов, выходов, переменных состояния и глобальных уравнений системы в виде (1.3).
а для более сложных систем оговаривается, что дать такие рекомендации трудно.
Поэтому ниже подробнее рассматривается классификация, в которой делается попытка связать выбор методов моделирования со всеми классами систем Основанием для этой классификации является степень организованности
Таблица 1.1
| Тик системы | УроисНЬ СЛОЖ)'«>СТН | Примеры | • |
|
L.™ ------------------ ---- ----------- . ----------------------- — 1 |
Статические структуры (остовы) | Кристаллы | |
| Неживые си- | Простые динамические структуры с задан- | Часовой мсха- | |
| стемы | ным законом поведения | шгзм | |
| Кибернетические системы с уираачяемымн | Термостат | ||
| : | циклами обратной связи | ||
| 1 ---- | Открытые системы с самосохранясмой | Клетки, | |
| структурой (первая ступень, на которой | гомеостат | ||
| возможно разделение на живое и неживое) | |||
| Живые организмы с низкой способностью | Растения | ||
| воспринимать информацию | |||
| Живые организмы с белое развитой способ- | Животные | ||
| Живые | ностью воспринимать информацию, но не | ||
| системы | обладающие самосознанием |
, |
|
| Системы, характеризующиеся самосознани- | Люди | V | |
| ем, мышлением и нетривиальным поведением |
t |
||
| Социальные системы | Социальные | 1 | |
| организации |
& |
||
| Трансцендентные системы или системы, ле- | »ь -•С | ||
| жащие в настоящий момент вне нашего по- |
, if |
||
| знания |
4f Jrt |
||
| 1 |
|
Jf" |
систем по степени организованности к ее роль в выборе методов моделирования систем. Впервые разделение систем по степени организованности по аналогии с классификацией Г.Саймона и А.Ньюэлла (хорошо структризованные, плохо структуризо-ванные и неструктуризованные проблемы [1.37]) было предложено В.В.Налимовым, который выделил класс хорошо организованных я класс плохо организованных или диффузных систем [1.34].
Позднее к этим двум классам был
курсовые - 700 р.
Работы, похожие на Реферат: Отрывок из учебника по теории систем и системному анализу
|