Реферат: Современные проблемы и концепции математического образования учителя физики

В. В. Афанасьев, Е. И. Смирнов

Математическое образование физика - что это? Естественно самоорганизующаяся в соответствии с физической сущностью субстанция в образовательном поле индивида или целенаправленный опыт освоения математической деятельности, достаточный для объяснения и оперирования с физическими явлениями и процессами? Эти и другие вопросы звучат особенно актуально в образовательной нише подготовки учителя физики в педвузе. Существенной особенностью подготовки физика является то, что в учебной деятельности логика проектирования и развертывания (дидактического раскрытия) содержания учебных предметов профессионального образования направлена на интериоризацию базовых учебных элементов (знаний, умений, навыков) в процессе приобретения, применения и преобразования опыта, в то время как для эффективности реализации профессионально-предметной подготовки учителя физики необходимо повторное (по отношению к школьному образованию) обращение в физических дисциплинах к базовым учебным элементам в расширенном и обобщенном качестве, в том числе с методологических и методических позиций. К тому же возникают дополнительные проблемы адекватности математического языка и средств для объяснения существа физических явлений и процессов на школьном уровне. При этом логика расширенного и методологического подхода к математическому образованию учителя физики может быть в полной мере реализуема и соответствовать инновационным тенденциям, разрабатываемым в настоящее время в технологиях профессиональной подготовки учителя. Имеется в виду, в частности, технология фундирования, разрабатываемая в Ярославском педагогическом университете и признанная в том смысле, что наши разработки утверждены Министерством образования в качестве Единых заказ-нарядов на фундаментальные исследования и практически реализуются введением экспериментального Государственного образовательного стандарта (приказ № 2046 от 14.05.2001) подготовки учителя математики (ведется интенсивное исследование теории и технологии фундирования школьных знаний в подготовке учителя физики).

Системогенез профессиональной подготовки предполагает анализ как объективных, так и субъективных условий становления будущего учителя. Изменения в структуре высшего педагогического образования России, появление средних школ разного профиля: лицеев, гимназий, колледжей и т.п., демократизация общественной жизни - имеют в своей основе коренной поворот к гуманистическим позициям функционирования современного образования. Способность и готовность учителя XXI века дать личности возможность получения образования необходимого уровня и глубины на любом отрезке ее жизнедеятельности становится теперь одной из основных тенденций развития современного образования. Современный этап развития образования выдвигает повышенные требования к профессиональной (особенно предметной) подготовке учителя, вооруженного новейшими методиками и технологиями обучения, творчески мыслящего создателя учебного процесса в школах XXI века.

В немалой степени эта тенденция коснулась содержания математического образования в среднем и высшем звене, равно как и теорий, концепций и методов обучения математике в естественнонаучной подготовке учителя. Индивидуализация и мотивация обучения, дифференцированный подход, использование новейших исследований в психологии, физиологии человека, педагогике для совершенствования процесса обучения, поиск оптимальных условий для усвоения сложного математического содержания требуют от будущего учителя физики не только высокой компетентности в предметной области, но и достаточной подготовленности к самообразованию, к проявлению творческой активности на основе профессиональной идентификации личности учителя и профессии.

Одной из ведущих задач педагогического процесса подготовки учителя физики средней (полной) школы является преобразование личности студента в учителя-профессионала, способного решать все многообразие задач, связанных с обучением и воспитанием школьников. Улучшение профессиональной подготовки учителя физики требует не только новых, более эффективных путей организации учебно-воспитательного процесса в педвузе, но и пересмотра структуры и содержания математической подготовки студентов-физиков, поднятия ее на технологический уровень. Поэтому рассмотрение педагогического процесса и математического образования будущих учителей физики, его задачи, планы, программы исходят из потребности поисков нового, оптимального в методах, средствах и формах обучения, способствующих формированию целостной системы научных знаний.

Проблема математического образования будущего учителя физики является многослойной и требует целостного и всестороннего рассмотрения. Это и вопросы предметной математической подготовки: структура, содержание, принципы, критерии, объем и т.п.; и вопросы общекультурной гуманитарной составляющей: развитие качеств мышления (анализ, синтез, конкретизация и т.д.), общеучебных умений, связанных с математической деятельностью, математического обеспечения физических теорий, охватывающего современные разделы математики, развитие творческой активности студентов в процессе восприятия физических теорий, в том числе через математическое моделирование.

Объективно значимость математической подготовки учителя физики в педвузе возрастает с каждым годом ввиду усиления профилизации школьного образования, гуманизации преподавания естественных дисциплин, объективизации процесса фундирования знаний на современном этапе развития образовательных процессов. При этом, однако, выявляется ряд негативных линий. Во-первых, это явная тенденция к минимизации использования математической деятельности в школьном физическом образовании (что особенно ярко проявляется в западных образовательных системах) и, во-вторых, существенное падение интереса к естественнонаучным дисциплинам, особенно в старших классах средней школы.

Анкетирование (проведенное Ю.П. Поваренковым в Ярославской области) более чем 1000 школьников дало следующие результаты

Экспериментальные исследования показывают, что учитель физики по окончании педагогического вуза имеет слабые практические навыки оперирования математическими понятиями: производной, интегралом, элементарными функциями, вероятностью, матрицами и т.п., к тому же усвоенными на формальном уровне. Математическое моделирование физических процессов понимается схоластически, с отсутствием вариативности, самостоятельности исследования и пониженным фоном творческой активности будущего учителя физики. В то же время содержание и объем математического образования не в полной мере обоснованы с методологических и с профессиональных позиций и к тому же перегружены второстепенными знаниями, применение которых в будущей профессиональной и социокультурной деятельности учителя физики неадекватно формируемой потребности.

Таким образом, если обратиться к фактическому состоянию дел в математическом образовании студента-физика, то можно обнаружить целый ряд противоречий.

Нами выделены следующие основные противоречия:

1) Между объективной целостностью математического блока знаний, умений, математических навыков и существующей структурой математической подготовки учителя физики.

Действительно, несколько десятилетий назад высшая математика в педвузах преподавалась физикам в виде отдельных математических дисциплин: математический анализ, геометрия, алгебра и теория чисел с общей трудоемкостью более 2000 часов. Ряд лет назад в соответствии с Государственным образовательном стандартом (требования к обязательному минимуму содержания и уровню подготовки по специальности "01.04.00 - физика" - 1995 год) был введен учебный предмет "высшая математика", объединяющий в себе содержание трех вышеперечисленных математических дисциплин с общей трудоемкостью около 1000 часов. Оставляя пока в стороне вопросы содержания учебной программы, заметим, что данный предмет составляет ядро математической подготовки и поэтому должен быть достойно представлен собственно математическими дисциплинами (т.е. предыдущий подход был более обоснованным).

Целостность (и интегративность) математических знаний при этом ни в коей мере не страдает, так как ее в последнем варианте (1995 г.) и не было (соответствующая учебная программа представляла собой формальный набор единиц учебного материала - далеко не полного и внутренне не взаимосвязанного). Отсутствие рядов Фурье, элементов функционального анализа и теории групп, интегральных уравнений и вариационного исчисления вряд ли положительно сказывалось на изучении таких разделов физики, как ядерная физика, оптика, механика, квантовая теория поля и др.

И вот в 2001 году выходит второе поколение ГОС по физике, где математика представлена с общей трудоемкостью 800 часов (с возможностью использования часов национально-регионального компонента - 195), при этом содержание требований к уровню математической подготовки выглядит, мягко говоря, странным. Дело в том, что не удовлетворены два важнейших принципа построения содержания образовательного стандарта: его объективизации и наличия универсального ядра. Дословно аннотация содержания выглядит так: математический анализ (в стандартной комплектации), далее функциональный анализ, вариационное исчисление, теория вероятностей и математическая статистика, исследование операций и т.д.

Но что отбирать в функциональном анализе? Теорию линейных самосопряженных операторов в гильбертовом пространстве или теорию пространств Соболева и обобщенных функций Шварца; спектральную теорию или гармонический анализ и преобразование Фурье медленно и быстро растущих обобщенных функций? А может быть, сильные и слабые сходимости в локально выпуклых пространствах или теорию диффузионных процессов? Все эти разделы функционального анализа имеют достаточно прочные физические корни и формально имеют право быть представленными в учебных планах. Однако беда в том, что для двух произвольно выбранных вузов пересечение содержания математической подготовки может оказаться пустым и в то же время не противоречащим стандарту. А как быть с вариационным исчислением: остановиться на формульных и геометрических вопросах или рассматривать глубокие разделы теории функций, вырожденных лагранжианов и континуальных интегралов Фейнмана. Можно ли успеть что-либо сказать о прямых методах вариацинного исчисления в решении краевых задач для дифференциальных уравнений в частных производных или о полях экстремалей и уравнении Гамильтона-Якоби?

Поэтому отсутствие обоснованных принципов отбора содержания математической подготовки будущих учителей физики, в том числе в методологическом плане, безусловно, может негативно сказываться на качестве их предметной подготовки.

2) Между возможностью моделирования физических явлений и процессов и формально-логическим стилем преподавания математических дисциплин.

Восприятие новых математических знаний студентами, в том числе будущими учителями физики, будет более осмысленным и устойчивым, если преподаватель воспользуется современными методами и подходами обучения математике, в частности, использованием "мягких" математических моделей по В.И. Арнольду [8] или метода наглядно-модельного обучения (технология этого метода активно разрабатывается на базе Ярославского педагогического университета).

3) Между естественным "формализмом" математического языка (и как следствие - формализмом знаний) и сущностью математических объектов (понятий, теорем, доказательств и т.п.), проявление которой в процессе обучения математике является важной методической проблемой.

Более того, в последние годы в преподавании физики заметно стала проявляться тенденция к "самообслуживанию". Речь идет о восполнении пробелов в содержании учебных программ (сознательно) по математике самими преподавателями физики в процессе изучения физических знаний. Например, при изучении квантовой электродинамики возникает необходимость обращения к понятию обобщенной функции и чисто математической задаче перемножения обобщенных функций. Конечно, преподаватель физики донесет формальную сторону вопроса до обучаемых, однако только специалист-математик сможет (имея на это достаточное время) проявить существо понятий, обращаясь к функционально-топологическим аспектам вопроса. Такое самодостаточное преподавание приводит к естественному "формализму" знаний, что наиболее выпукло проявляется на государственных экзаменах. Причем речь идет не только о таких понятиях, как спектр оператора, собственные значения, гильбертово пространство или самосопряженность атомных гамильтонианов, но и о таких базовых понятиях, как кратные и криволинейные интегралы, полный дифференциал и полная производная, градиент функции и т.п.

4) Между содержанием учебно-методического обеспечения математического образования физики в форме учебно-методических комплексов (УМК) (если таковые имеются, а фактически разрозненных компонентов УМК - методических указаний, пособий, учебников, программного обеспечения, рабочих программ и т.п.) и объективной необходимостью наличия целостной методической системы обучения будущих учителей физики.

Следует отметить, что вопросы математического образования будущих учителей физики неоднократно рассматривались в процессе подготовки ГОС в структуре Научно-методических советов России по физике и математике (1994-1996 гг.). Например, на совместном совещании НМС по физике и математике УМО ОППО Минобразования РФ и секции университетов и педвузов НМС по физике Госкомвуза РФ в сентябре 1995 года было принято решение о корректировке образовательного стандарта по математике для физиков и предложены конкретная структура и учебные программы по математике для будущих учителей физики. К сожалению, в Государственные требования к минимуму содержания и уровню подготовки выпускников по специальности "01.04.00 - физика" эти предложения не вошли, и до последнего времени мы работали с первоначальным вариантом 1994 года. О содержании последнего стандарта (2001) мы уже говорили.

5) Между ориентацией на построение содержания математического образования, исходя из его особенностей, и необходимостью учета психологических аспектов сенсорно-перцептивных процессов адекватного восприятия студентами-физиками математического содержания.

Физика и математика как учебные предметы, являясь основой естественнонаучного образования школьника и студента, несут в себе мощный гуманитарный потенциал, определяющий в том числе процессы социализации и адаптации личности к изменяющимся явлениям окружающего мира, равно как и стимулирующий развитие интеллектуальных сил и личностных качеств обучаемого.

Естественно, что физика всегда стремится решать свои задачи, опираясь на интуицию, аналогии и эксперимент, а математики хотят добиться логической завершенности модельности и целостности математических знаний, обслуживающих физические процессы и явления. Физическая наука на протяжение столетий стимулировала математические исследования. Так, механика Ньютона дала мощный толчок к развитию дифференциального и интегрального исчисления, механика упругих сред - тензорному анализу, термодинамика - гармоническому анализу, квантовая электродинамика - теории локально выпуклых пространств и обобщенных функций Л.Шварца и С.Л.Соболева, квантовая механика - теории неограниченных операторов в банаховом пространстве. Поэтому влияние физики и математики на формирование подструктур личности будет тем более весомым, если процесс их преподавания (равно как и отбор надлежащего содержания) будет максимально взаимообусловленным. При этом влияние физики на математику и математики на физику не является симметричным и имеет свои особенности в существе и форме проявления. Математика, объективно в высокой степени формализованная наука, требующая высокого уровня абстрагирования и отвлечения от реальностей действительного мира, нуждается в активизации конкретизационных, мотивационных и деятельностно-моделирующих процессов в ходе ее освоения. Это определяет следующие основные компоненты влияния физического содержания на освоение математики с развивающимся эффектом:

мотивационный (определяющий личностный смысл деятельности в направлении вектора цель - результат). Например, появление мотиваций, стимулированных физическим содержанием, может проявляться по следующим критериям: целостности (наличие антиципаций /предвосхищение будущего результата/ для проявления сущности целевого учебного элемента математики в ходе формирования когнитивного опыта школьника: антиципации могут актуализироваться как в репродуктивной, так и в продуктивной учебной деятельности; так, в первом случае таковыми могут быть физические задачи, явления, процессы, приводящие к мотивированному введению математических понятий и теорем; во втором случае возможна, например, квазиисследовательская деятельность школьников в малых группах по решению средствами математического аппарата физических задач); достижения (создание проблемных физических ситуаций, стимулирующих появление новой математической информации); фона (создание условий направленного восприятия активизацией ментальной /склад ума, мироощущение, мировосприятие/, перцептивной /непосредственное отражение действительности органами чувств/ и эмоционально-волевой сферы - исторические сведения, наглядность, эмоции и т.п.);

самоопределения (создание ситуативной /ограниченной определенными условиями/ доминанты /господствующий в данный момент очаг возбуждения в центральной нервной системе, обладающий повышенной восприимчивостью ко всем приходящим в нее раздражениям и способный оказывать тормозящее влияние на деятельность других нервных центров/ выбора социальной позиции школьника в процессе решения физических задач с максимальным использованием математических ресурсов);

прикладной (определяет приложение математических знаний к реальным процессам и способствует ориентации личности в окружающем мире);

практический (определяет процессы конкретизации математических абстракций физическими явлениями);

деятельностный (определяет процессы математического моделирования физических явлений и расчета физических процессов);

эвристический (способствует формированию и развитию математического знания, а также креативности /свойство мышления, характеризующееся способностью к преобразованию ментального опыта/ личности).

В то же время физика как педагогическая задача не может быть эффективно представлена лишь на феноменологической или полукачественной ступени абстракции (без достаточного математического осмысления), по крайней мере, в силу рассмотренного выше ее влияния на математику.

Может, однако, создаться впечатление, что математика (особенно в сфере образования) является средством для описания и объяснения физических явлений и процессов или средством для реализации алгоритмических процедур. "Существует широко распространенное заблуждение, что математика полезна для физиков лишь потому, что она дает средства для вычислений. На деле математика играет гораздо более тонкую роль, которая в конечном счете куда важнее. Когда создается удачная математическая модель физического явления, т.е. модель, которая позволяет делать точные вычисления и предсказания, то сама математическая структура модели открывает новые стороны этого явления" [2].

В более глубоком анализе влияние математического содержания на освоение физики типологизируется в следующих компонентах:

алгоритмико-вычислительном (определяющем возможность проведения алгоритмических процедур и численных расчетов физических явлений);

формализационном (определяющем степень формализации физических процессов и явлений): измерения, представления и преобразования величин, функциональные зависимости между физическими величинами, знаково-символическая формализация и графическая визуализация физических законов;

сущностном (определяющем возможность проникновения и вскрытия сущности физических явлений и процессов); это становится внешним агентом требований к математической подготовленности ввиду адекватности объяснения сути разнородных физических явлений и процессов информирования мыслительной культуры. Уровень математического образования должен удовлетворять объективные потребности в доказательности, логической завершенности формируемых математических знаний, устойчивости и прочности умений и навыков оперировать с математическими объектами в процессе обучения физике.

модельном (определяющем моделирование физических процессов и явлений), при этом, когда создается и анализируется удачная математическая модель физического явления, то создаются предпосылки для открытия новых сторон этого явления или процесса;

эвристическом (способствующем развитию физического знания и креативности личности).

Это становится важным аспектом математической подготовки студентов-физиков ввиду адекватности объяснения разнородных физических явлений и формирования математической культуры будущих учителей физики.

Концепция исследования представляет собой научные основы решения проблемы математического образования будущих учителей физики:

1. Педагогический процесс математического образования студента-физика определяется представлением о нем как о научно управляемом процессе,

имеющем целью достижение высокого уровня математической готовности выпускников педвузов к выполнению функций обучения, воспитания и развития обучаемых средствами математики,

связанном с реализацией общедидактических принципов: научности, доступности, гуманизации, дифференциации и т.д.,

организуемом с учетом современного состояния школьного образования: Федерального государственного стандарта полной (средней) школы, разнообразия форм средних учебных заведений, вариативности учебных программ и учебников, разработки новых педагогический технологий,

определяемом рядом системообразующих факторов: фундирования как процесса физической и углубления математической подготовки на основе базового школьного компонента, реализации технологии наглядно-модельного обучения математике, профессионально-педагогической направленности математического образования.

2. Эффективная организация учебно-методической деятельности студентов-физиков требует реализации для математической деятельности следующих структурообразующих принципов: фундирования, целостности, профессионально-педагогической направленности, наглядно-модельного обучения, оптимальности, развивающего обучения.

Реализация рассмотренных принципов в педагогической системе математического образования должна осуществляться в следующих компонентах содержания образования:

учебный план Предметного блока Государственного образовательного стандарта;

учебные программы (образовательные профессиональные программы) математических дисциплин;

теоретический и практический материал учебных дисциплин, отражающий содержание учебных программ;

методологическое и методическое обеспечение преподавания математики.

Данная типология согласуется с подходом к разработке теоретических основ содержания образования В.В.Краевского и И.Я.Лернера, которые различают три уровня проектируемого содержания: общетеоретический уровень (учебный план), уровень учебного предмета (программа) и уровень учебного материала (учебное пособие).

3. Педагогическая система математического образования учителя физики представляет собой целостный объект, имеющий следующие характеристики:

компоненты системы,

структура внутренних и внешних взаимосвязей,

функциональность,

интегративность,

обобщенность.

Анализ теоретических работ и реальная практика педагогической деятельности позволяют представить следующие основные компоненты педагогической системы:

мотивы,

целеполагание,

модели содержания и структуры математического образования,

средства, формы, условия,

результаты,

мониторинг функционирования системы.

Педагогическая система математического образования является важнейшей частью системы более высокого уровня профессиональной подготовки учителей физики - и функционирует в ее составе.

Целеполагающим компонентом системы математического образования будет выступать профессиограмма учителя физики, служащая ориентиром готовности будущего учителя физики к профессиональной деятельности.

4. В процессе обучения математике происходит развитие и трансформация мотивационной сферы студентов педвузов. Как указывает В.Д.Шадриков, "это развитие идет в двух направлениях: во-первых, общие мотивы личности трансформируются в трудовые; во-вторых, с изменением уровня профессионализации изменяется и система профессиональных мотивов" [4].

Поэтому предлагаются следующие принципы отбора содержания математической подготовки учителя физики в педвузе:

Социально-культурная и гуманитарная составляющая

Эта линия отражает сферу формирования элементов математического мышления студента-физика, математических навыков социокультурного уровня, внедрения активных методов обучения (наглядность, деловые игры, поисковые и т.п.), стимулирующих интерес к профессии и предмету обучения.

Прикладная составляющая

Содержание математического образования физика должно соответствовать потребности физических знаний в проявлении их сущности, необходима возможность конкретизации математических понятий на физических примерах, мотивация введения математических понятий рассмотрением реальных физических процессов.

Фундаментальная составляющая

Уровень математического образования должен удовлетворять объективной потребности, преемственности школьных и вузовских знаний, логической завершенности формируемых математических знаний, устойчивости и прочности формирования умений и навыков оперирования с математическими объектами.

Становление творческой активности

Математическое образование дает реальную возможность усилить влияние поисковых и эвристических методов обучения математике на формирование и становление творческой активности студентов-физиков.

Принцип наглядно-модельного обучения. Такому подходу к построению математического образования чужды формализм, начетничество, игнорирование или недостаточное внимание к субъекту восприятия сущности математики. Со времен великих педагогов (Я.А. Коменский, Т. Песталоцци, К.Д. Ушинский и др.) педагогическая мысль стремилась к такой организации учебного процесса, при которой достигается сознательное понимание смысла (сути) и содержания математических понятий. Один из таких путей - сделать процесс обучения математике наглядным, так как именно наглядное обучение позволяет учителю овладеть активными методами обучения и воспитания, способствует обеспечению принципов научности и доступности изложения материала, улучшению общекультурной подготовки учащихся, позволяет обеспечить разностороннее и полное формирование понятий, поддерживать интерес учащихся к предмету, к учебе, приводит к более высокому уровню развития математической культуры, в том числе математического языка и логического мышления, эстетического восприятия, творческого отношения к делу.

Основной задачей повышения эффективности применения наглядного метода обучения математике является отыскание и применение на практике активных методов формирования и организации учебной познавательной деятельности. Для решения поставленной проблемы следует выделить основные характерные черты изучаемого объекта, исходя из которых и дать определение наглядного обучения математике, указать средства его реализации в процессе учебной деятельности.

Наглядное обучение - это определенный вид деятельности как учителя, так и ученика [5]. Действие должно быть адекватно знанию, которое усваивается, при этом активная мыслительная деятельность обучаемых значительно обогащает процесс восприятия учебного материала. Таким образом, внешние действия учителя и внутренние действия обучаемых по выявлению содержания и формированию представлений являются неотъемлемыми элементами структуры наглядного обучения.

Следующий компонент концепции наглядного обучения - модельность, построение модели и ее усвоение. Наглядное обучение - это процесс создания "хорошо усваиваемых моделей" с опорой на нейро-физиологические и психологические механизмы восприятия. Моделирование является одним из составных компонентов наглядного обучения.

В процессе обучения мы формулируем модель существенных признаков объекта изучения, адекватных поставленной цели. Таким образом, наглядное обучение есть процесс, включающий в себя как построение модели, так и формирование адекватного результата внутренних действий обучаемых в процессе учебной деятельности. Предпочтение отдается "наглядной модели" в смысле опоры на устойчивые ассоциации, простые геометрические формы, психологические законы восприятия и нейро-физиологические механизмы памяти. Модель должна отражать суть понятия, формы или метода исследования.

В процессе формирования математических представлений о физических процессах приемами наглядного обучения существенную роль играет специфика математических знаний, умений, навыков и методов. Математика оперирует объектами, уже представляющими абстрагирование от действительного мира и, как правило, обобщающими разнообразные реальные и идеальные ситуации: интеграл как обобщение и абстрагирование понятий площади, длины, объема, но в то же время абсолютно непрерывная функция; производная как обобщение и абстрагирование понятий касательной, скорости, плотности, но в то же время переменная площадь, заключенная под непрерывной кривой. Эти идеальные объекты являются основными для формирования других абстракций: свертка функций, обобщенная производная - распределение, мера, преобразование Лапласа и т.д. Поэтому опоры для внутренних действий обучаемых в процессе наглядного обучения математике следует искать не только во внешних действиях учителя, но и среди остаточных фреймов - следов предыдущих знаний в памяти обучаемых.

В процессе выделения основных компонентов наглядного обучения мы пришли к следующему выводу: в процессе обучения математике студентов-физиков важно предварительно провести подготовку обучаемого к восприятию, четко поставить цель, затем не только предъявить объект изучения, но и организовать деятельность обучаемого при работе с объектом адекватно модели организованного набора математических знаний.

Применение наглядно-модельных методов обучения математике для студентов-физиков может выражаться как в специфических критериях отбора математического содержания, так и в технических единицах дидактического материала.

Принцип фундирования. Структурообразующим фактором проектируемых дидактических систем математического образования студентов-физиков в педвузе может являться концепция фундирования, предложенная академиком В.Д. Шадриковым. Фундирование школьных учебных элементов - это процесс создания условий (психологических, педагогических, организационно-методических) для актуализации базовых учебных элементов школьной и вузовской математики, адекватных физическому содержанию, с последующим теоретическим обобщением структурных единиц, раскрывающим их сущность, целостность и физическую обусловленность в направлении профессионализации знаний и формирования личности педагога. Принципиальным отличием формулируемой концепции фундирования является определение профессионально - ориентированной теоретической основы для спиралевидной схемы развертывания и моделирования базовых учебных элементов математики в направлении теоретического обобщения в системе математической подготовки студентов-физиков.

Принципы и критерии отбора учебного материала были обсуждены выше, приведем примеры технологических единиц в форме структурно-логических спиралей. Схема построения таких спиралей фундирования математического знания (умения, навыка, метода) дана на следующем рисунке.

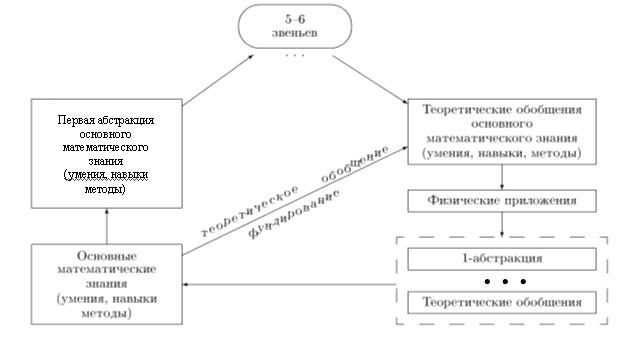
При этом желательно для n-ой абстракции основного математического знания (умения, навыка, метода) указывать и обсуждать не менее 2-х физических приложений (дидактически физические приложения могут предшествовать появлению n-ой абстракции, выполняя функции мотивационного блока). Более конкретно для основного понятия числа имеем структурно-логическую спираль:

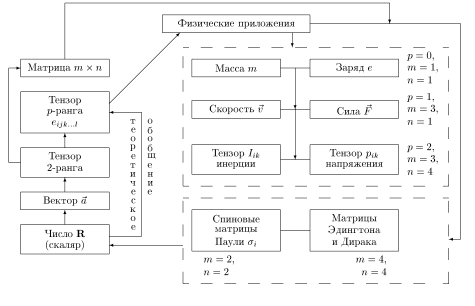
Выводы: математическое образование будущего учителя физики будет оптимальным, если:

Ввести раздельные математические дисциплины: математический анализ, геометрию, алгебру, теорию вероятностей и математическую статистику;

Ввести следующие дисциплины: вариационное исчисление (либо как часть математического анализа); теорию функций комплексного переменного, ряды Фурье (как часть математического анализа); теорию групп и тензорное исчисление (как часть алгебры); элементы функционального анализа (конкретизация разделов);

Определены общие и специальные принципы, определяющие направления развития системы математического образования физика в педвузе. К общим принципам относятся: принцип личностной ориентации, принцип профессионально-педагогической направленности, принцип целостности, принцип вариативности, принцип моделирования и принцип методологической определенности. К специальным принципам относятся принцип наглядного моделирования, принцип покрытия, принцип фундирования, принцип развивающего обучения.

Определена модель методической системы математического образования будущих учителей физики в единстве методологического, теоретического и общекультурного компонентов;

Дано теоретическое обоснование сущности математического образования будущего учителя физики как целостного процесса становления личности учителя, включающей систему математических знаний, систему общих интеллектуальных и практических умений и навыков, опыт творческой деятельности, опыт эмоционально-волевой деятельности;

Дана модель содержания математического образования будущих учителей физики, включающая общетеоретический уровень (учебный план), уровень учебного предмета (программы), уровень учебного материала (учебники, монографии, пособия, методические указания и т.п.), опыт творческой и эмоционально-волевой деятельности.

Конкретная проработка математического содержания подготовки учителя физики должна осуществляться вузами при содействии и контроле научно-методических советов России по физике и математике.

Список литературы

Джеффрис Г., Сквайрс Б. Методы математической физики. М.: Мир, 1970. 350 с.

Рид Е., Саймон Б. Методы современной математической физики. Функциональный анализ. М.: Мир, 1977. 354 с.

Афанасьев В.В. Формирование творческой активности студентов в процессе решения математических задач. Ярославль, 1996. 168 с.

Афанасьев В.В., Поваренков Ю.П., Смирнов Е.И., Шадриков В.Д. Подготовка учителя математики: Инновационные подходы. Учебное пособие. М.: Гардарики, 2001. 383 с.

Смирнов Е.И. Технология наглядно-модельного обучения математике. Ярославль, 1997. 283 c.

Анохин П.К. Философский смысл проблемы интеллекта // Вопросы философии. 1973. № 6.

Леонтьев А.Н. Деятельность, сознание, личность. М., 1975.

Арнольд В.И. "Жесткие" и "мягкие" математические модели. М.: МЦНМО, 2000.