Реферат: Многофункциональность упражнения и многофакторность умения
А.В. Ястребов, Ярославский государственный педагогический университет
В работе сформулированы два положения, связанные с процессом формирования математических умений. Проведено их обсуждение с точки зрения некоторых современных концепций преподавания математики.
Основные утверждения
Первое утверждение, которое мы назовём многофункциональностью упражнения, формулируется так: упражнение формирует, как правило, не одно умение, а целую группу умений.
Проиллюстрируем это на материале курса алгебры и теории чисел. Для этого рассмотрим следующую задачу.
Задача. Подкольцо Z кольца R порождает бинарное отношение T на R следующим образом:
![]()
![]()
![]()
![]() .
.
Является ли T отношением эквивалентности? Если да, то найдите фактор-множество R/T.
Прежде всего отметим, что появление такой задачи при изучении отношений эквивалентности вполне естественно. Действительно, при построении теории чисел в рамках базового курса алгебры и теории чисел мы вместо включения Z R используем включение Gm Z, где Gm - множество чисел, кратных m 0, 1, а вместо бинарного отношения T - отношение сравнения ≡ по модулю m ; сами же отношения T и ≡ определяются единообразно.
Доказательство того факта, что T - отношение эквивалентности, основано на свойствах операций над вещественными числами. Например, транзитивность доказывается следующим образом:
![]()
Переходя
к описанию фактор-множества нетрудно заметить, что любые различные числа
полусегмента [0, 1) попарно неэквивалентны, и что любое вещественное число
эвкивалентно одному из чисел данного полусегмента. Таким образом,
фактор-множество построено, однако результат построения недостаточно хорош,
поскольку с тем же основанием можно назвать фактор-множеством многие другие
объекты, например, полусегмент [a, a+1) при произвольном a, полуинтервал (а,
а+1], объединение сегмента и интервала ![]() и т.д. Для канонического описания
фактор-множества нужно вспомнить, что полусегмент [0, 1) находится во
взаимно-однозначном соответствии с полусегментом [0, 2 ), который, в
свою очередь, находится во взаимно-однозначном соответствии с окружностью S,
заданной стандартными параметрическими уравнениями. Образуя композицию этих
соответствий, мы можем получить каноническое отображение
и т.д. Для канонического описания
фактор-множества нужно вспомнить, что полусегмент [0, 1) находится во
взаимно-однозначном соответствии с полусегментом [0, 2 ), который, в
свою очередь, находится во взаимно-однозначном соответствии с окружностью S,
заданной стандартными параметрическими уравнениями. Образуя композицию этих
соответствий, мы можем получить каноническое отображение ![]() , определяемое
параметрическими уравнениями
, определяемое
параметрическими уравнениями
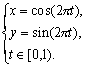
Итак, фактор-множество является окружностью: R/T=S.
Приведённая схема решения показывает, что задача по своему происхождению является алгебраической, результат формулируется на геометрическом языке, а значительная часть доказательства осуществляется с помощью техники, характерной для математического анализа. Действительно, данная задача формирует группу разнохарактерных умений.
Отступим от основной линии изложения и наметим развитие данной задачи в двух направлениях, геометрическом и алгебраическом.
Отношение
T на R порождает бинарное отношение T1![]() на множестве R2, которое
определяется следующим образом:
на множестве R2, которое
определяется следующим образом:
![]()
Другими словами, две точки из R2 находятся в бинарном отношении T1, если их первые координаты эквивалентны в смысле отношенияT.
Нетрудно доказать, что T1 - отношение эквивалентности. Из его определения вытекает, что для факторизации R2 = R R по T1 нужно профакторизировать по T первый множитель декартова произведения, откуда следует, что R2/T1=(R/T) R=S R. Очевидно, что декартово произведение окружности S на прямую R является цилиндром.
Аналогично, отношение T на R порождает бинарное отношение T2 на множестве R2, которое определяется следующим образом:
![]()
Другими словами, две точки из R2 находятся в бинарном отношении T2, если их соответственные координаты эквивалентны в смысле отношения T.
Нетрудно доказать, что T2 - отношение эквивалентности. Из его определения вытекает, что для факторизации R2 = R R по T2 нужно профакторизировать по T каждый множитель декартова произведения, откуда следует, что R2/T2 = (R/T) (R/T)=S S. Декартово произведение двух окружностей - это тор. Таким образом, исходная алгебраическая задача получила хорошее геометрическое продолжение.
Эту
же задачу можно рассматривать с точки зрения теории групп, поскольку (R, +) -
это группа. Каждое вещественное число a порождает класс эквивалентности ā
R/T. Если определить операцию сложения на R/T с помощью формулы ![]() то можно доказать, что
это определение корректно и что пара (R/T, +)образует группу.
то можно доказать, что
это определение корректно и что пара (R/T, +)образует группу.
Вспомним
теперь об отождествлении фактормножества с окружностью: классы эквивалентности
ā и ![]() из
фактормножества соответственно отождествляются с точками
из
фактормножества соответственно отождествляются с точками ![]()
![]() и
и ![]() на окружности. В силу этого
операция сложения классов индуцирует операцию сложения точек:
на окружности. В силу этого
операция сложения классов индуцирует операцию сложения точек: ![]() . Естественно поставить
вопрос о том, как найти положение точки C на окружности, зная положения точек A
и B. Совершенно аналогично можно построить операции над точками цилиндра и тора
и поставить задачу о выяснении геометрического смысла этих операций. Таким
образом, как исходная задача, так и её продолжение формирует целую группу
умений из различных разделов математики.
. Естественно поставить
вопрос о том, как найти положение точки C на окружности, зная положения точек A
и B. Совершенно аналогично можно построить операции над точками цилиндра и тора
и поставить задачу о выяснении геометрического смысла этих операций. Таким
образом, как исходная задача, так и её продолжение формирует целую группу
умений из различных разделов математики.
Второе из основных утверждений, которое мы назовём многофакторностью умения, формулируется так: умение формируется, как правило, под воздействием многих разнохарактерных упражнений.
Дело в том, что умение нельзя считать сформированным в момент сообщения студенту его формально-логической базы, т.е. формулы, теоремы, алгоритма и т.д. Для его полного формирования необходима как стадия пропедевтики, так и стадия применения. Последняя, в свою очередь, состоит из двух частей: непосредственного применения и вхождения умения в качестве составной части в более сложный комплекс умственных действий. Например, вряд ли можно считать, что учащийся овладел тригонометрическими формулами в тот момент, когда они были впервые выведены преподавателем или даже получены самостоятельно. Их полное освоение происходит в процессе решения тригонометрических уравнений и неравенств, доказательства тригонометрических тождеств, исследования тригонометрических функций, вычисления тригонометрических интегралов, действий с комплексными числами, записанными в тригонометрической форме, и.т.д. Умение приводить матрицу к ступенчатому виду оказывается полностью сформированным в результате решения систем линейных уравнений, исследования таких систем с параметрами, применения метода неопределённых коэффициентов в алгебое и математическом анализе, выполнения более чем полутора десятков алгоритмов линейной алгебры. Умение дифференцировать формируется не только при выполнении упражнений на технику дифференцирования, но также при исследовании функций и построении их графиков, при дифференцировании интегралов с переменным верхним пределом, при исследовании функций многих переменных, при изучении функций комплексного переменного.
Перечисленные и многие другие примеры выявляют одно объективное обстоятельство: многие математические умения и навыки, которые начали формироваться ещё в школе, доводятся до совершенства в вузе в процессе решения упражнений и задач самых разнообразных типов.
Основные утверждения в свете некоторых методических концепций
Рассмотрим сформулированные выше основные утверждения с точки зрения трёх методических концепций: авторской концепции обучения математике как модели научных исследований [5], теоретических основ подготовки преподавателей профильных школ О.А. Иванова [1] и технологии наглядно-модельного обучения Е.И. Смирнова [4].
Согласно первой из них обучение математике в педвузе должно быть моделью исследовательской работы в сфере математики и методики её преподавания [5. С.17]. При этом одним из свойств научной работы, подлежащих воспроизведению в учебном процессе, является современность ведущихся исследований. Моделирование этого свойства предполагает введение студентов в круг объектов, изучаемых наукой в настоящее введение студентов в круг объектов, изучаемых наукой в настоящее время, знакомство с типичными исследовательскими задачами [5. С.19-20]. Для педагогических вузов, в отличие от классических университетов, это чрезвычайно сложная задача, поскольку преподаватели вынуждены оставаться в рамках государственных образовательных стандартов, которые, к сожалению, достаточно бедны.
Покажем, что несмотря на свою простоту, задачи предыдущего раздела готовят студентов к восприятию таких современных математических понятий, как группы Ли и однородные пространства. В предыдущем разделе было показано, что на окружности, цилиндре и торе можно ввести алгебраические операции, удовлетворяющие аксиомам группы. Тем самым в поле зрения студентов возникает необычное явление, когда предмет изучения несёт на себе одновременно две разнотипные структуры, а именно, является и геометрическим объектом, и группой. Ретроспективный взгляд показывает, что эта ситуация встречалась достаточно часто, хотя ей быть может, и не уделялось должного внимания. Действительно, целый ряд хорошо знакомых геометрических объектов несёт на себе групповую структуру: прямая (группа R по сложению), прямая с выколотой точкой (группа R*=R\ 0 по умножению), открытый луч (группа положительных чисел по умножению), плоскость (группа R2 по сложению), плоскость с выколотой точкой (группа C*=C\ 0 по умножению). К этому списку из восьми примеров можно при желании добавить спирали на комплексной плоскости
![]()
![]()
каждая из которых образует мультипликативную группу. Их изучение естественно вписывается как в курс математического анализа, так и в курс дифференциальной геометрии. В перспективе, при изучении кватернионов, можно рассмотреть мультипликативную группу кватернионов с единичной нормой, или другими словами, трёхмерную сферу, несущую на себе групповую структуру. Отметим, что изучение кватернионов до недавнего времени включалось в программу педагогических вузов: см., например, [2. С. 299]. Таким образом, мы получаем достаточно богатую "зоологию" особых математических объектов, отталкиваясь от которой можно начать систематическое изучение групп Ли. Важно, что этот список примеров возник на базе весьма простой математической техники.
Для введения представлений об однородных пространствах наполним определение действия группы на множестве: группа G действует на множестве M, если задано отображение A:G M M, удовлетворяющее свойствам
Aghx=Ag(Ah)x, g, h G, x M.
Aex=x;
здесь
![]() - единица
группы.
- единица
группы.
Каждое действие A порождает отношение эквивалентности T' на множестве M заданное следующим образом:
![]()
Фактормножество M/T' называется однородным пространством относительно группы G.
Приведённая конструкция, несмотря на свою высокую абстрактность, имеет самое непосредственное отношение к курсу математики в педагогическом вузе. Действительно, в случае, когда G=Z, M=R, а действие задаётся равенством Ag(x)=g+x, простая проверка показывает, что T=T', и, следовательно, окружность является однородным пространством относительно группы Z. Естественно, что цилиндр и тор также оказываются однородными пространствами. В тезисах докладов [6] показано, что представление о трёх классических геометриях - евклидовой, сферической и Лобачевского - как об однородных пространствах может быть сформировано в базовом курсе геометрии для педагогического вуза; более полное изложение см. в [7. С.177-184]. Итак, мы вновь видим, что простые задачи позволяют приобщать студентов к первоначальным понятиям продвинутой математической теории.
Необходимость такого приобщения становится очевидной, если обратиться к теоретическим основам подготовки преподавателей математических школ. Определяя цели их подготовки, О.А. Иванов пишет: "Обучение на математических факультетах университетов должно быть направлено на подготовку специалиста - учителя высшей квалификации - с профессиональными навыками научного работника и учителя-методиста". При этом во главу угла ставятся так называемые интегративные курсы, которые характеризуются двумя особенностями: во-первых, изложение материала происходит не строго последовательно, а группируется вокруг определённых понятий, математических идей и утверждений; во-вторых, в этом изложении понятия и идеи элементарной математики связываются с общими математическими понятиями, идеями и утверждениями, известными студентам по базовым университетстким курсам [1. С.53]. Теоретико-методической основой соответствующего практикума по решению задач является понятие пучка задач, под которым понимается "такая их совокупность, определяющей характеристикой которой является наличие разнотипных взаимосвязей между отдельными составляющими эту совокупность задачами, обеспечивающее включение обратной связи в процесс их решения" [1. С. 58]. (Курсив мой - А.Я.)
Нетрудно видеть, что обсуждавшиеся выше математические задачи как раз и характеризуются наличием разнотипных взаимосвязей между рассматриваемыми объектами, группируясь при этом вокруг одного понятия - отношений эквивалентности. Таким образом, они могут рассматриваться и в качестве маленького фрагмента интегративного лекционного курса, и в качестве пучка задач из сопутствующего ему практикума.
Технология наглядно-модельного обучения уделяет значительное внимание процессу восприятия математических объектов. Так, Е.И. Смирнов пишет: "Процесс восприятия... предполагает наличие узловых, опорных, характерных, специфических свойств и качеств объекта восприятия, будь то приёмы деятельности, отражающие отдельное математическое знание, или организованный набор знаний.
... Актуальной является проблема такой организации процесса обучения математике, когда представления, возникающие в мышлении обучаемых, отражают основные, существенные, ключевые стороны предметов и явлений..." [4. С. 103].
Приведённые выше многофункциональные упражнения в полной мере учитывают указанную закономерность, поскольку формируют представления о фундаментальных приёмах деятельности математика: о факторизации и об отождествлении изоморфных объектов. Их узловой, опорный характер обусловлен, помимо прочего, их повторяемостью во времени. Действительно, к ним можно обращаться с различных точек зрения при изучении отношений эквивалентности, комплексных чисел, теории групп, теории функций комплексного переменного, оснований геометрии, поскольку окружность можно трактовать самыми разными способами: как множество комплексных чисел с единичным модулем, как мультипликативную подгруппу группы C*, как множество чисел вида eiφ, как однородное пространство.
Возможность многозначной трактовки одного и того же математического явления "формирует у будущих учителей важное профессиональное умение - видеть за единой формой разнообразное содержание, объединённое единой логической основой" [4. С. 209].
Мы видим, что многофункциональные упражнения, возникшие, казалось бы, из чисто математических соображений, оказываются полезными с точки зрения трёх различных педагогических концепций, возникших независимо друг от друга. Мы трактуем это обстоятельство как проявление закономерности, сформулированной А. Пуанкаре: "Размышлять о том, каким образом лучше всего внедрить понятия в девственный ум ребёнка, - значит в то же время размышлять о том, каким образом эти понятия были приобретены нашими предками; значит, следовательно, размышлять об их истинном происхождении, а это, по существу, значит размышлять об их истинной природе" [3. С. 286].
Список литературы
Иванов О.А. Теоретические основы построения специальной математической и методической подготовки преподавателей профильных школ. СПб.: Изд-во С.-Петерб. ун-та, 1997.
Куликов Л.Я. Алгебра и теория чисел. М.: Высшая школа, 1979.
Пуанкаре А. О науке. М.: Наука, 1983.
Смирнов Е.И. Технология наглядно-модельного обучения математике. Ярославль: Изд-во Ярославского гос. пед. ун-та, 1998.
Ястребов А.В. Научное мышление и учебный процесс - параллели и взаимосвязи. Ярославль: Изд-во Ярославского гос. пед. ун-та, 1997.
Ястребов А.В. Опыт изложения в задачах простейших фактов геометрии Лобачевского // Международная научная конференция "Лобачевский и современная геометрия. Казань, 18-22 августа 1992. Тезисы докладов Ч.II. Казань: Изд-во Казанского ун-та, С.83-84.
Ястребов А.В. Моделирование научных исследований как средство оптимизации обучения студента педагогического вуза: Дис. ... д-ра пед. наук. / Ярославск. гос. пед. ун-т им. К.Д. Ушинского. / Ярославль, 1997. 386 с.