Реферат: Преобразование Фурье
Анатолий Карташкин
В основе преобразования Фурье (ПФ) лежит чрезвычайно простая, но исключительно плодотворная идея – почти любую периодическую функцию можно представить суммой отдельных гармонических составляющих (синусоид и косинусоид с различными амплитудами A, периодами Т и, следовательно, частотами ω). Пример одной из таких функций S(t), состоящей из гармоник Сi(t), приведен на рис.1.
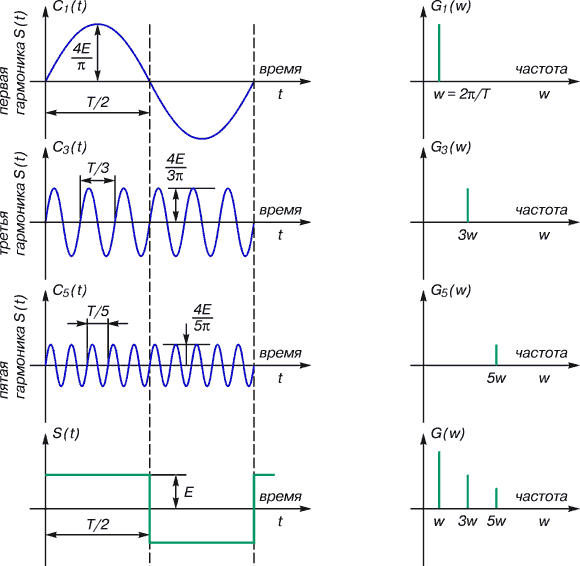
Рис. 1. Представление прямоугольного импульса суммой гармонических составляющих
Понятия «изобразить в частотной области некую функцию от времени» и «нарисовать спектр этой функции» – равнозначны. Если скользнуть по рис.1 взглядом по горизонтали слева направо, то свершится переход от какой-либо функции времени к ее спектру – благодаря «магическому стеклу» ПФ. А нижняя часть рисунка есть иллюстрация одного из основных принципов ПФ – спектр суммарной функции времени равен сумме спектров ее гармонических составляющих.
Неоспоримым достоинством ПФ является его гибкость – преобразование может использоваться как для непрерывных функций времени, так и для дискретных. В последнем случае оно называется дискретным ПФ – ДПФ.
Для получения дискретной функции времени надо подвергнуть процессу дискретизации непрерывную функцию времени. Это изображено на рис.2. Вырезаем отдельные значения из непрерывной функции, выстраивая дискретную функцию времени. Период одного цикла его работы Tд называется «периодом дискретизации», или «интервалом дискретности».
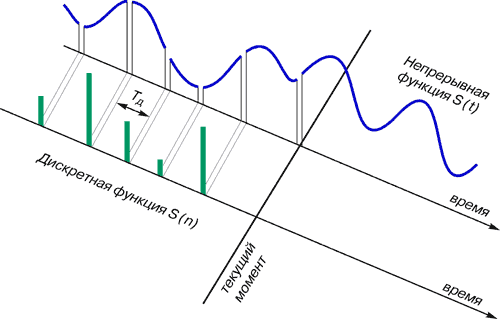
Рис. 2. Дискретное представление непрерывной функции
ПФ часто применяется при решении задач, возникающих в теории автоматического регулирования и управления, в теории фильтрации и т.д. Разберем один из примеров. Имеется некий линейный фильтр – изготовленный то ли в виде набора спаянных между собой резисторов, конденсаторов и катушек индуктивности, то ли в виде модульной конструкции интегральных микросхем. Известен также входной сигнал (на рис.3 в качестве входного сигнала изображена дельта-функция, то есть импульс исчезающе короткой длительности и бесконечно большой амплитуды). Необходимо определить, какой сигнал появится на выходе нашего фильтра.
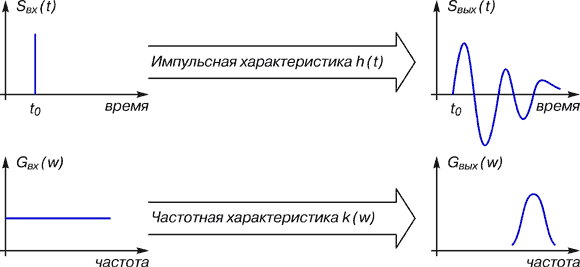
Рис. 3. Исследование линейного фильтра
Ход решения этой задачи зависит от того, какую позицию мы предпочтем. Выберем временной путь решения (верхняя половина рис.4) – придется входной сигнал записать как функцию времени SBX(t) и использовать импульсную характеристику фильтра h(t), то есть математическую запись его работы во времени. Отправимся по частотному пути (нижняя половина рис.4) – нужно будет оперировать уже не с самим входным сигналом, а с его спектром gbx(ω). Δа и алгоритм работы нашего фильтра потребуется представить в частотной области – в виде частотной характеристики K(ω). Δля этого воспользуемся помощью опять-таки «магического стекла» ПФ.
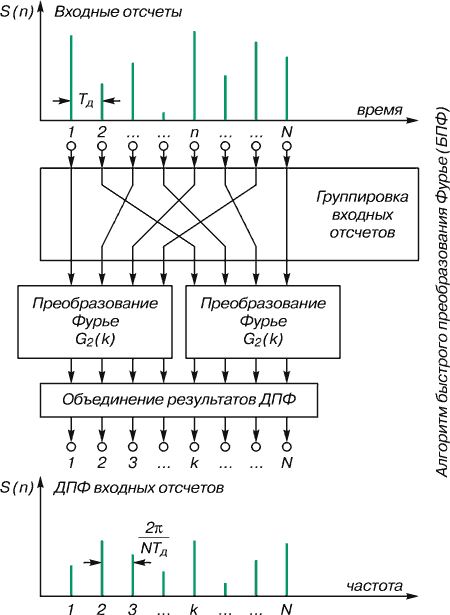
Рис. 4. Быстрое преобразование Фурье
Итак, два пути – какой из них избрать? По-видимому, тот, который проще. Во всяком случае, в большинстве практических задач предпочтение отдается частотному направлению.
Если выполнять ДПФ входной последовательности, так сказать, впрямую – строго по исходной формуле, то потребуется много времени (особенно если количество входных отсчетов велико). Конструктивнее использовать принцип «разделяй и властвуй», лежащий в основе алгоритма БПФ. Согласно ему входная последовательность делится на группы (например, четные и нечетные отсчеты), и для каждой из них выполняется ДПФ, а затем полученные результаты объединяются. В итоге получается ДПФ входной последовательности – и существенная экономия времени. Поэтому описанный алгоритм так и назвали – быстрое преобразование Фурье.
Список литературы
Лаврус В.С. Практика измерений в телевизионной технике. – К.: НиТ, 1996.
Карташкин А. Уйти, чтобы вернуться.
| Управление сложными системами | |
|
Лекция №1. 11.02.2003 Раздел 1. Основные понятия теории сложности 1.1. Сложность Сложность - свойство современных систем управления. Различают ... Импульсное устройство (ключ), замыкаясь в дискретные равноотстоящие моменты времени (t = i=T, i = 0, 1, 2, ., где i - период повторения, а T - период дискретности), преобразует ... По аналогии с непрерывными системами: (отношение Z-преобразования сигнала на выходе фильтра к Z-преобразованию входного сигнала при нулевых обратных условиях). |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Приборы для радиоизмерения | |
|
Московский Государственный Технический Университет Гражданской Авиации Кафедра теоретической радиотехники Контрольная работа по дисциплине ... Для сигнала u (t) вводят спектральную функцию (или спектральную плотность), определяемую прямым преобразованием Фурье. Тогда на выходе смесителя возникают колебания с комбинационными частотами, в том числе с разностной частотой fс - fг (t). Сигнал с разностной (и меняющейся во времени) частотой ... |
Раздел: Рефераты по коммуникации и связи Тип: контрольная работа |
| Моделирование схемы усилителя НЧ на МДП-транзисторах | |
|
Содержание 1. Задание 2. Технические характеристики усилителя НЧ 3. Теоретические сведенья 4. Описание схемы усилителя 4.1 Описание 4.2 Конструкция и ... При выполнении дискретных преобразований Фурье, используется только второй период собственной составляющей переходной характеристики (извлечённой из выходной цепи). Особенно заметны комбинационные частоты вида f1-f2, f1-2f2, 2f1-f2, так как они, как правило, не содержатся в спектре даже сложного входного сигнала. |
Раздел: Рефераты по коммуникации и связи Тип: курсовая работа |
| Методы позиционирования и сжатия звука | |
|
Современные звуковые карты. Аннотация В данной курсовой работе изучаются различные аспекты применения звуковых карт. Рассматриваются способы получения ... Выполняемые математические операции могут либо имитировать работу традиционных аналоговых средств обработки (микширование двух сигналов - сложение, усиление/ослабление сигнала ... DCT использует тот факт, что пиксели в блоке и сами блоки связаны между собой (т.е. коррелированны), поэтому происходит разбивка на частотные фурье компоненты (в итоге получается ... |
Раздел: Рефераты по информатике, программированию Тип: дипломная работа |
| Дискретизация и квантование изображений | |
|
ИСТОРИЧЕСКИЙ ОЧЕРК. Еще с середины 40-ых годов , специалисты по радиоэлектроники начали задумываться над возможностью применения специализированных ... Эта теорема утверждает , что если сигнал f(t) имеет преобразование Фурье Sf(w) отличное от нуля при частотах меньших 2pFm . На вход фильтра мы подаем сумму импульсов с амплитудами равными f(kDt) Разложение сигнала f(t) в ряд Котельникова указывает на технический способ передачи непрерывной функции ... |
Раздел: Рефераты по радиоэлектронике Тип: реферат |