Реферат: Использование цепей Маркова в моделировании социально-экономических процессов
Пусть {![]() ,
, ![]() , ...,
, ..., ![]() } - множество возможных состояний некоторой физической
системы. В любой момент времени система может находиться только в одном
состоянии. С течением времени система переходит последовательно из одного
состояния в другое. Каждый такой переход называется шагом процесса.
} - множество возможных состояний некоторой физической
системы. В любой момент времени система может находиться только в одном
состоянии. С течением времени система переходит последовательно из одного
состояния в другое. Каждый такой переход называется шагом процесса.
Для описания эволюции этой системы введем
последовательность дискретных случайных величин ![]() ,
, ![]() ,...,
,..., ![]() ,... Индекс n играет роль времени. Если в момент времени n
система находилась в состоянии
,... Индекс n играет роль времени. Если в момент времени n
система находилась в состоянии ![]() , то мы будем считать, что
, то мы будем считать, что ![]() = j. Таким образом, случайные величины являются номерами
состояний системы.
= j. Таким образом, случайные величины являются номерами
состояний системы.
Последовательность ![]() ,
, ![]() ,...,
,..., ![]() ,... образует цепь Маркова, если для любого n и любых
,... образует цепь Маркова, если для любого n и любых ![]() ,
, ![]() , ...,
, ..., ![]() ,...
,...
P(![]() =j /
=j / ![]() =
= ![]() , ...,
, ..., ![]() =i)=P(
=i)=P(![]() =j /
=j / ![]() =i).
=i).
Для цепей Маркова вероятность в момент времени n
попасть в состояние ![]() , если известна вся предыдущая история изучаемого процесса,
зависит только от того, в каком состоянии находился процесс в момент n-1. То
есть при фиксированном "настоящем" "будущее" не зависит от
"прошлого". Свойство независимости "будущего" от
"прошлого" при фиксированном "настоящем" называется марковским
свойством.
, если известна вся предыдущая история изучаемого процесса,
зависит только от того, в каком состоянии находился процесс в момент n-1. То
есть при фиксированном "настоящем" "будущее" не зависит от
"прошлого". Свойство независимости "будущего" от
"прошлого" при фиксированном "настоящем" называется марковским
свойством.
Вероятности ![]() (
( ![]() =j /
=j / ![]() =i), i, j=1,2,..., r называются вероятностями перехода из
состояния
=i), i, j=1,2,..., r называются вероятностями перехода из
состояния ![]() в состояние
в состояние ![]() за один шаг.
за один шаг.
Цепь Маркова называется однородной, если вероятности
перехода ![]() не зависят от n, т.е. если вероятности перехода не зависят от
номера шага, а зависят только от того, из какого состояния и в какое
осуществляется переход. Для однородных цепей Маркова вместо
не зависят от n, т.е. если вероятности перехода не зависят от
номера шага, а зависят только от того, из какого состояния и в какое
осуществляется переход. Для однородных цепей Маркова вместо ![]() будем писать
будем писать ![]() .
.
Вероятности перехода удобно располагать в виде квадратной матрицы
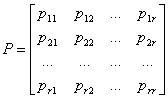
Матрица P называется матрицей вероятностей перехода однородной цепи Маркова за один шаг. Она обладает следующими свойствами:
а) ![]() ;
;
б) для всех i: ![]()
Квадратные матрицы, для которых выполняются условия а) и б), называются стохастическими.
Вектор ![]() , где
, где ![]() =P(
=P(![]() ), i=1,2...,r называется вектором начальных вероятностей.
), i=1,2...,r называется вектором начальных вероятностей.
Свойства однородных цепей Маркова полностью определяются вектором начальных вероятностей и матрицей вероятностей перехода.
Приведем пример: Завод выпускает телевизоры
определенного типа. В зависимости от того, находит ли данный тип телевизора спрос
у населения, завод в конце каждого года может находиться в одном из состояний:
состояние 1 – спрос есть, состояние 2 – спроса нет. Пусть вероятность сохранить
состояние 1 в в следующем году с учетом возможного изменения спроса равна ![]() , а вероятность изменить состояние 2 с учетом мероприятий по
улучшению выпускаемой модели равна
, а вероятность изменить состояние 2 с учетом мероприятий по
улучшению выпускаемой модели равна ![]() . Тогда процесс производства на данном заводе можно описать
цепью Маркова с матрицей переходов:
. Тогда процесс производства на данном заводе можно описать
цепью Маркова с матрицей переходов:
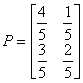
В конкретных случаях для описания эволюции цепи
Маркова вместо явного выписывания матрицы P используют граф, вершинами которого
являются состояния цепи, а стрелка, идущая из состояния ![]() в состояние
в состояние ![]() с числом
с числом ![]() над ней показывает, что из состояния
над ней показывает, что из состояния ![]() в состояние
в состояние ![]() возможен переход с вероятностью
возможен переход с вероятностью ![]() . В том случае, когда
. В том случае, когда ![]() , соответствующая стрелка не проводится.
, соответствующая стрелка не проводится.
Можно показать, что матрица вероятностей перехода цепи Маркова за n шагов равняется n-ой степени матрицы P вероятностей перехода за один шаг. Для однородной цепи Маркова при любом m выполняется равенство
P(![]() )=P(
)=P(![]() ).
).
Но последняя вероятность есть вероятность перехода из
состояния ![]() в состояние
в состояние ![]() за n шагов.
за n шагов.
§2. Теорема о предельных вероятностях.
В 1930 году Дж.Биркгофом и Дж.фон Нейманом была сформулирована и доказана одна из основных эргодических теорем – теорема о предельных вероятностях:
Если при некотором ![]() все элементы матрицы
все элементы матрицы ![]() =[
=[![]() ] положительны, то существуют пределы
] положительны, то существуют пределы
![]()
![]() , i,j =1,2,...,r.
, i,j =1,2,...,r.
Предельные вероятности ![]() не зависят от
начального состояния
не зависят от
начального состояния ![]() и являются единственным решением системы уравнений
и являются единственным решением системы уравнений
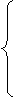
| (1) |
![]() , j=1, 2, ..., r.
, j=1, 2, ..., r.
Физический смысл этой теоремы заключается в том, что
вероятности нахождения системы в состоянии ![]() практически не зависят от того, в каком состоянии она
находилась в далеком прошлом.
практически не зависят от того, в каком состоянии она
находилась в далеком прошлом.
Цепь Маркова, для которой существуют пределы ![]() , называется эргодической. Решение (
, называется эргодической. Решение (![]() ,
,![]() ,...,
,...,![]() ) написанной выше системы (1) называется стационарным
распределением вероятностей для марковской цепи с матрицей перехода P = [
) написанной выше системы (1) называется стационарным
распределением вероятностей для марковской цепи с матрицей перехода P = [![]() ].
].
Если из состояния![]() система может перейти в состояние
система может перейти в состояние ![]() с положительной вероятностью за конечное число шагов, то
говорят, что
с положительной вероятностью за конечное число шагов, то
говорят, что ![]() достижимо из
достижимо из ![]() .
.
Состояние ![]() называется существенным, если для каждого состояния
называется существенным, если для каждого состояния ![]() , достижимого из
, достижимого из ![]() ,
, ![]() достижимо из
достижимо из ![]() . Если же для хотя бы одного j
. Если же для хотя бы одного j ![]() достижимо из
достижимо из ![]() , а
, а ![]() не достижимо из
не достижимо из ![]() , то
, то ![]() - несущественное состояние.
- несущественное состояние.
§3. Области применения цепей Маркова.
Цепи Маркова служат хорошим введением в теорию случайных процессов, т.е. теорию простых последовательностей семейств случайных величин, обычно зависящих от параметра, который в большинстве приложений играет роль времени. Она предназначена, главным образом, для полного описания как долговременного, так и локального поведения процесса. Приведем некоторые наиболее изученные в этом плане вопросы.
Броуновское движение и его обобщения – диффузионные процессы и процессы с независимыми приращениями. Теория случайных процессов способствовала углублению связи между теорией вероятностей, теорией операторов и теорией дифференциальных уравнений, что, помимо прочего, имело важное значение для физики и других приложений. К числу приложений относятся процессы, представляющие интерес для актуарной (страховой) математики, теории массового обслуживания, генетики, регулирования дорожного движения, теории электрических цепей, а также теории учета и накопления товаров.
Мартингалы. Эти процессы сохраняют достаточно свойств цепей Маркова, чтобы для них оставались в силе важные эргодические теоремы. От цепей Маркова мартингалы отличаются тем, что когда текущее состояние известно, только математическое ожидание будущего, но необязательно само распределение вероятностей, не зависит от прошлого. Помимо того, что теория мартингалов представляет собой важный инструмент для исследования, она обогатила новыми предельными теоремами теорию случайных процессов, возникающих в статистике, теории деления атомного ядра, генетике и теории информации.
Стационарные процессы. Самая старая из известных эргодических теорем, как отмечалось выше, может быть интерпретирована как результат, описывающий предельное поведение стационарного случайного процесса. Такой процесс обладает тем свойством, что все вероятностные законы, которым он удовлетворяет, остаются инвариантными относительно сдвигов по времени. Эргодическую теорему, впервые сформулированную физиками в качестве гипотезы, можно представить как утверждение о том, что при определенных условиях среднее по ансамблю совпадает со средним по времени. Это означает, что одну и ту же информацию можно получить из долговременного наблюдения за системой и из одновременного (и одномоментного) наблюдения многих независимых копий той же самой системы. Закон больших чисел есть не что иное, как частный случай эргодической теоремы Биркгофа. Интерполяция и предсказание поведения стационарных гауссовских процессов, понимаемых в широком смысле, служат важным обобщением классической теории наименьших квадратов. Теория стационарных процессов – необходимое орудие исследования во многих областях, например, в теории связи, которая занимается изучением и созданием систем, передающих сообщения при наличии шума или случайных помех.
Марковские процессы (процессы без последействия) играют огромную роль в моделировании систем массового обслуживания (СМО), а также в моделировании и выборе стратегии управления социально-экономическими процессами, происходящими в обществе. В качестве примера рассмотрим управляемые цепи Маркова.
§4. Управляемые цепи Маркова. Выбор стратегии.
Завод по изготовлению телевизоров, находясь в состоянии 1, может увеличить спрос путем организации рекламы. Это требует добавочных затрат и уменьшает доход. В состоянии 2 завод может увеличить вероятность перехода в состояние 1 путем увеличения затрат на исследования. Выделим две стратегии. Первая состоит в отказе от затрат на рекламу и исследования, а вторая - в согласии на них. Пусть матрицы переходных вероятностей и матрицы доходов для данных стратегий имеют вид:
![]()
![]()
![]()
![]()
В рассмотренной ситуации имеет место управляемая цепь Маркова. Управление соответствует выбору стратегии.
Пусть каждому состоянию ![]() соответствует конечное множество
соответствует конечное множество ![]() решений (или
альтернатив), элементы которого обозначим номерами
решений (или
альтернатив), элементы которого обозначим номерами ![]() . Пространством стратегий К называется прямое произведение
множеств решений
. Пространством стратегий К называется прямое произведение
множеств решений ![]() .
.
Пусть в i-м состоянии имеется не одно, а ![]() множеств переходных
вероятностей
множеств переходных
вероятностей ![]() . При
. При ![]() имеем случай
неуправляемой цепи Маркова. Если система находится в состоянии
имеем случай
неуправляемой цепи Маркова. Если система находится в состоянии ![]() и принимается решение
и принимается решение
![]() то
то
- она получает доход ![]() ;
;
- ее состояние в следующий момент времени определяется
вероятностью ![]() , где
, где ![]() - вероятность того,
что система из состояния
- вероятность того,
что система из состояния ![]() при выборе решения
при выборе решения ![]() перейдет в состояние
перейдет в состояние ![]() .
.
Таким образом, смысл ![]() -го решения в i-м состоянии заключается в выборе одного
набора переходных вероятностей
-го решения в i-м состоянии заключается в выборе одного
набора переходных вероятностей ![]() из
из ![]() возможных.
Предполагается, что доход
возможных.
Предполагается, что доход ![]() ограничен при всех
ограничен при всех ![]() и
и ![]() .
.
Кроме того,
![]() ,
, ![]() при всех
при всех ![]() и
и ![]() .
.
Управляемой цепью Маркова называется конструкция, задаваемая
параметрами ![]() , где К-решения, Р-вероятности переходов, r-доходы. Доход,
полученный за несколько шагов, является случайной величиной, зависящей от
начального состояния и принимаемых в каждый момент времени решений.
, где К-решения, Р-вероятности переходов, r-доходы. Доход,
полученный за несколько шагов, является случайной величиной, зависящей от
начального состояния и принимаемых в каждый момент времени решений.
Назовем решение, принимаемое в конкретный момент, частным управлением. Тогда управление есть последовательность решений в моменты n = 1, 2, ... Качество управления можно оценить средним суммарным доходом (при конечном времени) или среднем доходом в единицу времени (при бесконечном времени).
Пусть ![]() (2)
(2)
Стратегией ![]() называется
последовательность решений
называется
последовательность решений
![]()
![]()
где ![]() - вектор вида (2), i-я компонента которого, обозначаемая
через
- вектор вида (2), i-я компонента которого, обозначаемая
через ![]() , является решением, принимаемым в состоянии
, является решением, принимаемым в состоянии ![]() в момент п. Другими словами, задание стратегии означает полное
описание в каждый момент времени t =1, 2, ..., п, ... конкретных решений,
которые должны были бы приниматься в i-м состоянии , если бы система находилась
в нем в рассматриваемый момент.
в момент п. Другими словами, задание стратегии означает полное
описание в каждый момент времени t =1, 2, ..., п, ... конкретных решений,
которые должны были бы приниматься в i-м состоянии , если бы система находилась
в нем в рассматриваемый момент.
Стратегия ![]() обозначается через
обозначается через ![]() и называется стационарной. Стратегия
и называется стационарной. Стратегия ![]() называется марковской,
если решение
называется марковской,
если решение ![]() , принимаемое в каждом конкретном состоянии, не зависит от
предшествующих состояний и принимавшихся в них решений. В случае марковской
стратегии решения
, принимаемое в каждом конкретном состоянии, не зависит от
предшествующих состояний и принимавшихся в них решений. В случае марковской
стратегии решения ![]() могут зависеть только
от момента времени п.
могут зависеть только
от момента времени п.
Обозначим произвольную конечную часть стратегии через ![]() . Пусть зафиксированы произвольная стратегия
. Пусть зафиксированы произвольная стратегия ![]() некоторый момент времени п. Если в этот момент система
находилась в состоянии
некоторый момент времени п. Если в этот момент система
находилась в состоянии ![]() , то в следующий (п+1)-й момент времени она будет находиться
в состоянии
, то в следующий (п+1)-й момент времени она будет находиться
в состоянии ![]() с вероятностью
с вероятностью ![]() , где
, где ![]() . Тогда матрица переходных вероятностей в момент п имеет вид
. Тогда матрица переходных вероятностей в момент п имеет вид
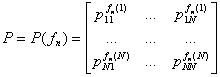
Таким образом, при фиксированной стратегии ![]() получаем цепь Маркова
с матрицами перехода
получаем цепь Маркова
с матрицами перехода ![]()
Обозначим ![]() - вектор суммарных средних доходов, полученных до любого
момента n включительно, для некоторой стратегии
- вектор суммарных средних доходов, полученных до любого
момента n включительно, для некоторой стратегии ![]() . Стратегия
. Стратегия ![]() максимизирующая
максимизирующая ![]() , то есть удовлетворяющая неравенству
, то есть удовлетворяющая неравенству
![]() ≥
≥![]() при любых
при любых ![]()
называется оптимальной
Верны следующее утверждения:
Утверждение 1. Для бесконечного времени существует оптимальная стационарная стратегия.
Утверждение 2. Для конечного времени существует оптимальная марковская стратегия.
Таким образом, решение (при бесконечном времени) зависит только от состояния, в котором находится система, и не зависит ни от момента времени, ни от всей предыдущей траектории последовательности состояний и принятых решений). В случае конечного времени оптимальная стратегия является марковской, т. е. может зависеть еще и от момента времени принятия решения.
Список литературы
1. «Теория выбора и принятия решений»: учебное пособие. И.М. Макаров, Т.М. Виноградская, А.А. Рубчинский, В.Б. Соколов. Москва, изд. «Наука», 1982.
2. «Теория вероятностей» Е.С. Вентцель. Москва, изд. «Наука», 1969.