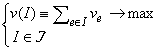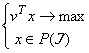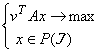Статья: Симметрии многогранника системы независимости

Пусть E = { e1,e2,,en} - некоторое множество мощности n. Системой независимости на множестве E называется непустое семейство J его подмножеств, удовлетворяющее условию: если Jи I, то I.

Множества семейства называется независимыми множествами. Максимальные по включению множества из называются базисами.

Автоморфизмом системы независимости называется такое взаимооднозначное отображение  множества E на себя, что (I){(e) | eI}для любого независимого множества I. Группу автоморфизмов системы независимости будем обозначать через Aut().

Пусть RE - евклидово пространство, ассоциированное с E посредством взаимоодназначного соответствия между множеством координатных осей пространства RE и множеством E. Иными словами, RE можно понимать как совокупность вектор-столбцов размерности n с вещественными компонентами, индексированными элементами множества E. Всякому S E сопоставим его вектор инциденций по правилу: xSe= 1 при eS , xSe= 0 при eS. Очевидно, что это правило задает взаимооднозначное соответствие между 2E и вершинами единичного куба в RE. Многогранник системы независимости определим как P() = Conv(xI | I). Ясно, что векторы инциденций независимых множеств системы независимости , и только они, являются вершинами многогранника P() [4].

Пусть PRE - произвольный многогранник. Симметрией многогранника P назовем такое невырожденное аффинное преобразование  пространства RE, что (P){(x) | xP}=P. Как известно, всякое невырожденное аффинное преобразование  определяется невырожденной (nn)-матрицей A и сдвигом hRE, то есть (x)=Ax+h при xRE [1]. Очевидно, что невырожденное аффинное преобразование  пространства RE является симметрией многогранника P() тогда и только тогда, когда для любого I существует такое J, что (xI) = xJ.

Симметрию с нулевым сдвигом будем называть линейной симметрией. Очевидно, что множество всех симметрий многогранника P является группой относительно суперпозиции отображений, а множество линейных симметрий - ее подгруппой. Группу симметрий многогранника P мы будем обозначать через S(), а ее подгруппу линейных симметрий - через L().

Ранее в [3] была доказана изоморфность групп L() и Aut() для матроида , в [2] - изоморфность группы линейных симметрий многогранника паросочетаний и группы автоморфизмов соответствующего графа. Пользуясь аналогичными методами, легко доказать изоморфность групп L() и Aut() для произвольной системы независимости .

В настоящей работе показано, что группа симметрий многогранника системы независимости выписывается с помощью подгруппы L() и семейства некоторых специальных преобразований пространства RE.

Рассмотрим задачу комбинаторной оптимизации на системе независимости с аддитивной целевой функцией:

где ve0 - вес элемента eE. Пусть имеется симметрия многогранника P со сдвигом xH. Тогда задача (1) сводится к задаче, размерность которой не больше, чем E-H.

Ниже приведены понятия и факты, необходимые для дальнейшего изложения.

Пусть H. H-отображением будем называть линейное невырожденное преобразование  пространства RE, удовлетворяющее условию: для любого I существует такое J, что (xI) = xJH, где под JH подразумевается симметрическая разность множеств J и H.

Без ограничения общности будем считать, что размерность многогранника P равна n, ибо в противном случае существует элемент eЕ, не содержащийся ни в каком независимом множестве и, следовательно, вместо E можно рассматривать множество E{e} .

2.  Структура группы симметрий системы независимости

Итак, будем считать, что у нас зафиксирована система независимости на множестве E={e1,e2,,en}; RE-пространство, ассоциированное с E; P-многогранник системы независимости .

Так как , то для всякой симметрии  со сдвигом h найдется такое H, что h=xH. Таким образом, группу S() можно разбить на непересекающиеся классы , где SH - класс симметрий многогранника P(), имеющих сдвиг xH. Это позволяет свести описание группы S() к описанию.

Лемма 1. Пусть SH, a 1 - аффинное невырожденное преобразование пространства RE. Тогда 1SH, если и только если существует такое 2L(), что 1 = jj2.

Доказательство. Так как L() и SH являются подмножествами группы S(), то j1 = jj2S(). Очевидно, что j1 имеет сдвиг xH. Обратно, если j1  SH, то j2 = j-1j1S(), причем с нулевым сдвигом. Следовательно, j2L().

Таким образом, наличие какой-либо (любой) симметрии из SH позволяет с помощью группы L() найти весь класс SH.

Лемма 2. Пусть j - невырожденное преобразование пространства RE. Преобразование jSH тогда и только тогда, когда j=j1j2, где

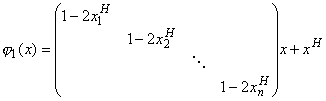
a j2 - H-отображение.

Доказательство. Прямыми вычислениями легко убедиться, что j1(xS) = xSH для любого SE, и j1-1=j1.

Если 2 - H-отображение, то для любого Iсуществует такой J, что 2(xI) = xJH. То есть 12(xI) = x(JH)H = xJ.

Следовательно,  = 12 - симметрия многогранника P и jSH.

Если же jSH, то для любого I существует такой J, что (xI)=xJ. Следовательно, 2(xI) =1-1(xI) = 1-1(xJ) = 1(xJ) = xJH

Значит, 2 - H-отображение. Данная лемма дает возможность свести поиск представителя класса SH к поиску одного H-отображения. Причем, если H-отображений для данного H не существует, то SH=.

Поиск H-отображения существенно упрощается с помощью следующего предложения.

Предложение 1. Матрица H-отображения  булева.

Доказательство. Так как {ej} для любого j{1n}, то ,по определению H-отображения, вектор (x{ej}), являющийся j-м столбцом матрицы отображения, булев, что и требовалось доказать.

3.  Понижение размерности задачи на системе независимости

Рассмотрим оптимизационную задачу (1) и перейдем к полиэдральной постановки этой задачи

где v - это вектор, компоненты которого - веса соответствующих элементов. Очевидно, что решение задачи (2), при условии "поиска по вершинам", будет являться вектором инциденций решения задачи (1). Кроме того, если существует симметрия многогранника P с матрицей A и сдвигом h, и x* решение задачи

то вектор x = Ax*+h - решение задачи (2).

Предложение 2. Пусть (x) = Ax+xH - симметрия многогранника P и v - произвольный вектор с положительными компонентами. Тогда вектор vTA имеет по крайней мере H неположительных компонент.

Доказательство. По лемме 2, симметрия  представима в виде суперпозиции отображений 1, описанного в лемме 2, и H-отображения 2. Матрица A является произведением матриц преобразований 1 и 2. Так как HH{H | J}, то существует такое множество I, что 2 (xI) = xH. Причем, так как любое подмножество H принадлежит H, то в силу линейности 2, IH. Следовательно, матрица преобразования 2 принимает вид

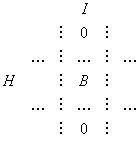
Здесь I и H - столбцы и строки, соответствующие элементам из этих множеств, а блок B - некоторая булевa матрица. При умножении матрицы преобразования 2 на матрицу преобразования 1 блок B заменяется на блок (-B). Затем, при умножении вектора vT на матрицу A, получается вектор, у которого компоненты, соответствующие элементам множества I, неположительные. Очевидно, что элементы, имеющие неположительные веса, не принадлежат оптимальному множеству задачи (3). Следовательно, исключая из рассмотрения эти элементы, переходим к задаче

где v* = vTA, D-совокупность элементов, у которых соответствующие компоненты вектора v* неположительные. Вектор инциденций решения этой задачи есть оптимальный вектор задачи (3). Причем, по предыдущему предложению, размерность задачи (4) не больше, чем E-H.

Пример 1. Пусть E = {1,2,3,4}, - система независимости, базисы которого являются множества {1,2,3} и {3,4}. Пусть H={1,3}. Тогда матрица H-отображения принимает вид

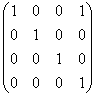
a симметрия многогранника системы независимости -

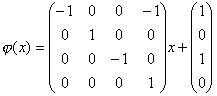
Пусть вектор весов v = (3,1,4,2), тогда вектор новых весов будет равен

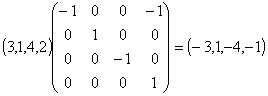
и после отбрасывания элементов c отрицательными весами получаем множество {2} , состоящее из одного элемента, которое и будет оптимальным для задачи с новыми весами. Следовательно вектор инциденций решения исходной задачи будет

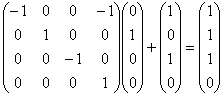
То есть оптимальное множество исходной задачи есть множество {1,2,3}.

Список литературы

Емеличев В.А., Ковалев М.М., Кравцов М.К. Многогранники, графы, оптимизация.- М.:Наука, 1981.

Симанчев Р.Ю. Линейные симметрии многогранника паросочетаний и автоморфизмы графа // Вестник Омского университета, 1996. N.1. C.18-20.

Червяков О.В. Линейные симметрии и автоморфизмы матроида //   Фундаментальная и прикладная математика. ОмГУ, 1994, с. 81- 89.

Conforti M., Laurent M. On the facial structure of independence system polyhedra // Math. of operations research. 1988. V.13. N. 4. P. 543 - 555.