Статья: Вычисление собственных чисел и собственных функций опрератора Штурма-Лиувилля на полуоси
Абзалимов Р.Р.
В
настоящей работе предлагается метод расчета приближенных собственных чисел и
собственных функций краевой задачи на полуоси для дифференциального уравнения
второго порядка. Для численного расчета собственных чисел интервал ![]() заменяется на
заменяется на ![]() , после чего
задача решается на конечном отрезке. Точность приближенных собственных чисел
будет зависеть от выбора граничного условия в точке R.
, после чего
задача решается на конечном отрезке. Точность приближенных собственных чисел
будет зависеть от выбора граничного условия в точке R.
I. Регулярная задача
Рассмотрим следующую краевую задачу:
![]() , (1.1)
, (1.1)
![]() , (1.2)
, (1.2)
![]() . (1.3)
. (1.3)
Здесь предполагается, что q(x) кусочно-непрерывна на [a, b]. Наряду с данной задачей рассмотрим дифференциальные операторы вида:
![]() , (1.4)
, (1.4)
![]()
с граничными условиями
![]() , (1.5)
, (1.5)
![]() , (1.6)
, (1.6)
где
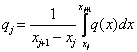 .
(1.7)
.
(1.7)
Под собственными функциями краевой задачи (1.4)-(1.6) будем понимать функцию y(x), удовлетворяющую следующим условиям (см. [1]):
![]() ;
;
![]() ;
;
![]() удовлетворяет граничным условиям (1.5) и
(1.6);
удовлетворяет граничным условиям (1.5) и
(1.6);
![]() удовлетворяет так называемым условиям
сопряжения
удовлетворяет так называемым условиям
сопряжения
![]() (1.8)
(1.8)
В
каждом интервале ![]() решения
решения ![]() уравнения
(1.4) имеют вид:
уравнения
(1.4) имеют вид:
![]() . (1.9)
. (1.9)
Из условий сопряжения (1.8) и (1.9) имеем:
 , (1.10)
, (1.10)
где
![]() ,
, ![]() выписываются явно (i=1,2; j=1,2; k=1..N).
Таким образом, получаем:
выписываются явно (i=1,2; j=1,2; k=1..N).
Таким образом, получаем:
 (1.11)
(1.11)
Из
первого краевого условия получаем зависимость ![]() от
от ![]() , затем,
подставляя во второе краевое условие (1.6), получаем уравнение для собственных
значений задачи (1.4)-(1.6):
, затем,
подставляя во второе краевое условие (1.6), получаем уравнение для собственных
значений задачи (1.4)-(1.6):
![]() ,
(1.12)
,
(1.12)
где
![]() выписывается явно.
выписывается явно.
Пусть
![]() - собственные значения и
- собственные значения и ![]() - соответствующие им собственные функции
задачи (1.4)-(1.6), где через h обозначено
- соответствующие им собственные функции
задачи (1.4)-(1.6), где через h обозначено
![]() ,
,
и
пусть![]() - собственные
значения задачи (1)-(3) и
- собственные
значения задачи (1)-(3) и ![]() соответствующие им собственные функции. Введем
обозначение:
соответствующие им собственные функции. Введем
обозначение:
![]() . (1.13)
. (1.13)
Заметим
прежде, что ![]() при
при ![]() .
.
Тогда имеет место следующая
ТЕОРЕМА 1.1 Справедливы равенства
![]() ,
(1.14)
,
(1.14)
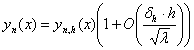 . (1.15)
. (1.15)
Доказательство.
Вначале докажем равенство (1.15). Для этого рассмотрим уравнение (1.1) на
интервале ![]() . Представим
ее в виде
. Представим
ее в виде
![]() , (1.16)
, (1.16)
где
![]() вычисляется по формуле (1.7). Для уравнения
(1.16) получаем интегральные уравнения:
вычисляется по формуле (1.7). Для уравнения
(1.16) получаем интегральные уравнения:
 ,
,
 .
.
Применяя метод последовательных приближений, получаем:
 , (1.17)
, (1.17)
где
![]() - решения уравнения (1.4).
- решения уравнения (1.4).
Следовательно, для всего промежутка [0,p] справедливо равенство (1.15).
Из (1.15) нетрудно установить неравенство:
![]() , (1.18)
, (1.18)
где
![]() при
при ![]() .
.
Тогда имеет место следующее равенство:
 (1.19)
(1.19)
при
![]() , где
, где ![]() - оператор Штурма-Лиувилля задачи (1.1)-(1.3),
а
- оператор Штурма-Лиувилля задачи (1.1)-(1.3),
а ![]() - оператор задачи (1.4)-(1.6). Из (1.18) и
(1.19) нетрудно показать справедливость оценки (1.14). Теорема доказана.
- оператор задачи (1.4)-(1.6). Из (1.18) и
(1.19) нетрудно показать справедливость оценки (1.14). Теорема доказана.
Следствие
1.1 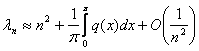 ,
,
 .
.
Следствие
1.2 ![]() , где
, где ![]() - характеристическое уравнение для собственных
значений задачи (1.4)-(1.6),
- характеристическое уравнение для собственных
значений задачи (1.4)-(1.6), ![]() - характеристическое уравнение для собственных
значений задачи (1.1)-(1.3).
- характеристическое уравнение для собственных
значений задачи (1.1)-(1.3).
Следствие
1.3 ![]() и
и ![]() совпадают со
всеми корнями уравнения
совпадают со
всеми корнями уравнения ![]() .
.
Следствие
1.4 ![]() образуют полную систему собственных функций.
образуют полную систему собственных функций.
II.
Сингулярная задача. Случай ![]() .
.
Будем рассматривать задачу
![]() , (2.1)
, (2.1)
![]() , (2.2)
, (2.2)
где
![]() монотонно, т.е. уравнение (2.1) имеет не более
одной точки поворота. Таким образом, для любого
монотонно, т.е. уравнение (2.1) имеет не более
одной точки поворота. Таким образом, для любого ![]() . В случае,
когда
. В случае,
когда ![]() , спектральная
задача имеет дискретный спектр. Из представленного метода решения регулярной
задачи следует, что
, спектральная
задача имеет дискретный спектр. Из представленного метода решения регулярной
задачи следует, что ![]() ; таким
образом, для каждого
; таким
образом, для каждого ![]() задачи на полуоси ставится в соответствие своя
регулярная задача на конечном отрезке
задачи на полуоси ставится в соответствие своя
регулярная задача на конечном отрезке ![]() . Если бы мы
знали все значения собственных функций
. Если бы мы
знали все значения собственных функций ![]() ,
соответствующие собственным числам
,
соответствующие собственным числам ![]() задачи на
полуоси, в точке
задачи на
полуоси, в точке ![]() , то, решая
задачи на конечном промежутке
, то, решая
задачи на конечном промежутке ![]() с дополнительным граничным условием
с дополнительным граничным условием ![]() , мы могли бы
вычислить все собственные числа задачи на
, мы могли бы
вычислить все собственные числа задачи на ![]() достаточно точно. Исходя из сказанного, можно
утверждать, что погрешность определения собственных чисел тем меньше, чем
точнее выбор второго краевого условия. В связи с этим рассмотрим два краевых
условия
достаточно точно. Исходя из сказанного, можно
утверждать, что погрешность определения собственных чисел тем меньше, чем
точнее выбор второго краевого условия. В связи с этим рассмотрим два краевых
условия ![]() (условие Дирихле) и
(условие Дирихле) и ![]() (условие Неймана). Пусть
(условие Неймана). Пусть ![]() - собственные числа задач на конечном
промежутке с дополнительными условиями Дирихле и Неймана соответственно. С
помощью метода решения регулярной задачи доказываются следующие утверждения:
- собственные числа задач на конечном
промежутке с дополнительными условиями Дирихле и Неймана соответственно. С
помощью метода решения регулярной задачи доказываются следующие утверждения:
ТЕОРЕМА 2.1 Справедлива асимптотическая формула собственных чисел задачи на полуоси
 , (2.3)
, (2.3)
где
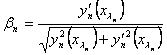 [1]
.
[1]
.
Справедливость теоремы 2.1 следует из следствия 1.1.
ТЕОРЕМА 2.2 Справедливо неравенство:
![]() .
(2.4)
.
(2.4)
Доказательство теоремы 2.2 можно провести с помощью функций распределения собственных чисел (см. [2]) или с помощью метода, предложенного в первой части работы, и следствия 1.1.
Замечание
В случае полуограниченного оператора (![]() ), данный
выбор краевых условий позволяет получать лишь верхнюю и нижнюю оценку
собственных чисел.
), данный
выбор краевых условий позволяет получать лишь верхнюю и нижнюю оценку
собственных чисел.
Следствие
2.1 ![]() , где
, где ![]() - длина промежутка
- длина промежутка ![]() .
.
Пример
 .
.
Известно,
что ![]() , где
, где ![]() вычисляется
явно. Из следствия 2.1 следует:
вычисляется
явно. Из следствия 2.1 следует:
 .
.
III.
Сингулярная задача. Случай ![]() .
.
Будем рассматривать задачу
![]() , (2.1)
, (2.1)
![]() . (2.2)
. (2.2)
Имеет место следующая (см. [3])
ТЕОРЕМА
3.1 Пусть потенциальная функция ![]() удовлетворяет
следующим условиям
удовлетворяет
следующим условиям
![]() ;
;
![]() , при
, при ![]() ;
;
![]() сохраняет знак для больших
сохраняет знак для больших ![]() ;
;
![]() , где
, где ![]() , при
, при ![]() ;
;
 .
.
Тогда
спектр оператора ![]() - чисто дискретный и состоит из двух серий
собственных чисел, уходящих на
- чисто дискретный и состоит из двух серий
собственных чисел, уходящих на ![]() и
и ![]() .
.
Аналогично
(как и для полуограниченного оператора) задача на полуоси для расчета
собственных чисел ![]() заменяется на регулярную задачу, т.е. интервал
заменяется на регулярную задачу, т.е. интервал
![]() заменяется на
заменяется на ![]() , где
, где ![]() - достаточно большое положительное число с
дополнительным краевым условием
- достаточно большое положительное число с
дополнительным краевым условием ![]() . Нетрудно
установить, что погрешность приближенных собственных чисел неполуограниченного
оператора (при
. Нетрудно
установить, что погрешность приближенных собственных чисел неполуограниченного
оператора (при ![]() ) стремится к
нулю при
) стремится к
нулю при ![]() . С помощью
решения регулярной задачи доказывается следующая
. С помощью
решения регулярной задачи доказывается следующая
ТЕОРЕМА
3.2 Пусть выполнены все условия теоремы 3.1. Тогда если ![]() - собственные числа задачи (2.1)-(2.2) на
конечном промежутке
- собственные числа задачи (2.1)-(2.2) на
конечном промежутке ![]() с дополнительным краевым условием
с дополнительным краевым условием ![]() , то
справедливо равенство
, то
справедливо равенство ![]() для всех
для всех ![]() .
.
Замечание 1 Известны более общие условия дискретности спектра задачи (2.1)-(2.2) (см. например [4]).
Замечание
2 Для расчета собственных чисел ![]() задачи (2.1)-(2.2), промежуток
задачи (2.1)-(2.2), промежуток ![]() заменяется на
заменяется на ![]() , где
, где ![]() - достаточно большое положительное число, с
краевыми условиями
- достаточно большое положительное число, с
краевыми условиями ![]() и
и ![]() .
.
IV.
Сингулярная задача. Случай ![]() .
.
Будем рассматривать задачу
![]() , (3.1)
, (3.1)
![]() (3.2)
(3.2)
с дополнительными условиями:
![]() ;
;
![]() голоморфна в точке
голоморфна в точке ![]() , причем
, причем ![]() ;
;
![]() при
при ![]() монотонно, и
монотонно, и ![]() , где
, где ![]() ;
;
![]() при
при ![]() ,
, ![]() .
.
Данная
задача рассматривалась в работе Е.ПЖидкова. и А.Г.Соловьева (см. [5]).
Известно, что задача имеет собственные числа и собственные функции такие, что
все ее собственные числа простые, отрицательные и образуют бесконечно
возрастающюю последовательность ![]() с единственной предельной точкой
с единственной предельной точкой ![]() , а
собственные функции
, а
собственные функции ![]() , отвечающие
собственным значениям
, отвечающие
собственным значениям ![]() , имеют в
интервале
, имеют в
интервале ![]() в точности
в точности ![]() нулей. В этом случае справедливы все
результаты, полученные для случая полуограниченного оператора.
нулей. В этом случае справедливы все
результаты, полученные для случая полуограниченного оператора.
Пример
 .
.
Известно
(см. [3]), что ![]() - собственные числа.
- собственные числа.
Введем
обозначения: ![]() - приближенные собственные числа, полученные
Е.П.Жидковым и А.Г.Соловьевым, а
- приближенные собственные числа, полученные
Е.П.Жидковым и А.Г.Соловьевым, а ![]() - приближенные собственные числа, полученные
методом, описанным выше. Были рассчитаны собственные числа, которые
представлены в таблице (см. ниже). Используя асимптотическую формулу (2.3),
можно показать (достаточно грубая оценка), что
- приближенные собственные числа, полученные
методом, описанным выше. Были рассчитаны собственные числа, которые
представлены в таблице (см. ниже). Используя асимптотическую формулу (2.3),
можно показать (достаточно грубая оценка), что
![]() ,
,
где
![]() вычисляется явно. Для более точной асимптотики
необходимо точно решить уравнение
вычисляется явно. Для более точной асимптотики
необходимо точно решить уравнение
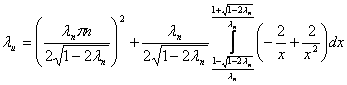 .
.
| n |
|
|
|
Промежуток | ||
|
|
|
|
||||
| 1 | 0.2500 | 0.25000… | 0.247… |
|
|
(1.16,6.82) |
| 2 | 0.1111 | 0.11107… | 0.111… |
|
|
(1.06,16.9) |
| 3 | 0.0625 | 0.06249… | 0.063… |
|
|
(1.03,30.9) |
| 4 | 0.0400 | 0.39995… | 0.041… |
|
|
(1.02,48.9) |
| 5 | 0.0277 | 0.0277715 | 0.028… |
|
|
(1.01,70.9) |
Список литературы
Митрохин С.И. // ДАН. 1997. Т. 356. № 1. С. 13-15.
Рид, Саймон. Методы современной математической физики. М.: Мир, 1977. Т. 1, 4
Титчмарш. Разложения по собственным функциям, связанные с дифференциальными уравнениями второго порядка. Т. 1. М.: Наука, 1960. 276 с.
Султанаев Я.Т. // ДАН. 1984. Т. 276. № 5. С. 1072-1074.
Жидков Е.П., Соловьев А.Г. // ЖВММФ. 1999. Т. 39. № 3. С. 1098-1118.