–°—В–∞—В—М—П: –Я–Њ–і—К–µ–Љ –Є–љ–≤–∞—А–Є–∞–љ—В–Њ–≤ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є—Е –≥—А—Г–њ–њ
–Р.–Э. –Ч—Г–±–Ї–Њ–≤, –Ю–Љ—Б–Ї–Є–є –≥–Њ—Б—Г–і–∞—А—Б—В–≤–µ–љ–љ—Л–є –њ–µ–і–∞–≥–Њ–≥–Є—З–µ—Б–Ї–Є–є —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В, –Ї–∞—Д–µ–і—А–∞ –∞–ї–≥–µ–±—А—Л
–Я—Г—Б—В—М
G –њ—А–Њ—Б—В–∞—П –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–∞—П –≥—А—Г–њ–њ–∞ –Њ–і–љ–Њ–≥–Њ –Є–Ј —В—А–µ—Е –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є—Е —В–Є–њ–Њ–≤ - B, C, D,
–љ–∞–і –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Є –Ј–∞–Љ–Ї–љ—Г—В—Л–Љ –њ–Њ–ї–µ–Љ K –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є. –У—А—Г–њ–њ–∞ G=G(n)
–Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Є –≤–ї–Њ–ґ–µ–љ–∞ –≤ GL(n) –і–ї—П –њ–Њ–і—Е–Њ–і—П—Й–µ–≥–Њ n [8]. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –і–Є–∞–≥–Њ–љ–∞–ї—М–љ–Њ–µ
–і–µ–є—Б—В–≤–Є–µ –≥—А—Г–њ–њ—Л G –љ–∞ ![]() - m
—Н–Ї–Ј–µ–Љ–њ–ї—П—А–∞—Е –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞
- m
—Н–Ї–Ј–µ–Љ–њ–ї—П—А–∞—Е –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ ![]() –Љ–∞—В—А–Є—Ж M(n)
—Б–Њ–њ—А—П–ґ–µ–љ–Є—П–Љ–Є. –Т–Њ–Ј–љ–Є–Ї–∞–µ—В –Є–љ—В–µ—А–µ—Б–љ–∞—П –Ј–∞–і–∞—З–∞ - –Њ–њ–Є—Б–∞—В—М –Ї–Њ–ї—М—Ж–Њ –Є–љ–≤–∞—А–Є–∞–љ—В–Њ–≤
In,m=K[M(n)m]G(n) . –Т –њ—А–µ–і–ї–∞–≥–∞–µ–Љ–Њ–є —А–∞–±–Њ—В–µ –±—Г–і–µ—В –і–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ
–µ—Б—В–µ—Б—В–≤–µ–љ–љ—Л–є —Н–њ–Є–Љ–Њ—А—Д–Є–Ј–Љ
–Љ–∞—В—А–Є—Ж M(n)
—Б–Њ–њ—А—П–ґ–µ–љ–Є—П–Љ–Є. –Т–Њ–Ј–љ–Є–Ї–∞–µ—В –Є–љ—В–µ—А–µ—Б–љ–∞—П –Ј–∞–і–∞—З–∞ - –Њ–њ–Є—Б–∞—В—М –Ї–Њ–ї—М—Ж–Њ –Є–љ–≤–∞—А–Є–∞–љ—В–Њ–≤
In,m=K[M(n)m]G(n) . –Т –њ—А–µ–і–ї–∞–≥–∞–µ–Љ–Њ–є —А–∞–±–Њ—В–µ –±—Г–і–µ—В –і–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ
–µ—Б—В–µ—Б—В–≤–µ–љ–љ—Л–є —Н–њ–Є–Љ–Њ—А—Д–Є–Ј–Љ ![]() , –Ї–Њ—В–Њ—А—Л–є
–Є–љ–і—Г—Ж–Є—А–Њ–≤–∞–љ –Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Є–Љ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ–Љ
, –Ї–Њ—В–Њ—А—Л–є
–Є–љ–і—Г—Ж–Є—А–Њ–≤–∞–љ –Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Є–Љ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ–Љ ![]() , –≥–і–µ
, –≥–і–µ ![]() —В–Њ–≥–і–∞ –Є —В–Њ–ї—М–Ї–Њ
—В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞
—В–Њ–≥–і–∞ –Є —В–Њ–ї—М–Ї–Њ
—В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ ![]() , –Є–ї–Є
, –Є–ї–Є ![]() (–і–ї—П
—Б–Є–Љ–њ–ї–µ–Ї—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–ї—Г—З–∞—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –і—А—Г–≥–Њ–µ, –Ј–і–µ—Б—М –Ј–∞–љ—Г–ї—П—О—В—Б—П –≤—Б–µ —Н–ї–µ–Љ–µ–љ—В—Л –≤–љ–µ
"—Ж–µ–љ—В—А–∞–ї—М–љ–Њ–≥–Њ"
(–і–ї—П
—Б–Є–Љ–њ–ї–µ–Ї—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–ї—Г—З–∞—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –і—А—Г–≥–Њ–µ, –Ј–і–µ—Б—М –Ј–∞–љ—Г–ї—П—О—В—Б—П –≤—Б–µ —Н–ї–µ–Љ–µ–љ—В—Л –≤–љ–µ
"—Ж–µ–љ—В—А–∞–ї—М–љ–Њ–≥–Њ" ![]() -–±–ї–Њ–Ї–∞). –Э–∞
–Њ—Б—В–∞–ї—М–љ—Л—Е –Љ–µ—Б—В–∞—Е –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ —В–Њ–ґ–і–µ—Б—В–≤–µ–љ–љ–Њ.
-–±–ї–Њ–Ї–∞). –Э–∞
–Њ—Б—В–∞–ї—М–љ—Л—Е –Љ–µ—Б—В–∞—Е –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ —В–Њ–ґ–і–µ—Б—В–≤–µ–љ–љ–Њ.
–Т—Б–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ—Л–µ —Б–≤–µ–і–µ–љ–Є—П –Њ –Љ–Њ–і—Г–ї—П—Е —Б —Е–Њ—А–Њ—И–µ–є —Д–Є–ї—М—В—А–∞—Ж–Є–µ–є (–Ї—А–∞—В–Ї–Њ –Љ–Њ–і—Г–ї–Є —Б –•–§), –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –≤ [5].
–Ь—Л
–±—Г–і–µ–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –Є–і–µ—О –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–∞ —В–µ–Њ—А–µ–Љ—Л 2 –Є–Ј [5]. –Я—Г—Б—В—М ![]() .
.
C–ї—Г—З–∞–є
B, D. –Ь—Л –±—Г–і–µ–Љ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—В—М, —З—В–Њ ![]() . –Я–Њ–і—Е–Њ–і—П—Й–Є–Љ
–Њ–±—А–∞–Ј–Њ–Љ –Є–Ј–Љ–µ–љ—П—П –±–∞–Ј–Є—Б, –Љ—Л –Љ–Њ–ґ–µ–Љ —Б—З–Є—В–∞—В—М, —З—В–Њ
. –Я–Њ–і—Е–Њ–і—П—Й–Є–Љ
–Њ–±—А–∞–Ј–Њ–Љ –Є–Ј–Љ–µ–љ—П—П –±–∞–Ј–Є—Б, –Љ—Л –Љ–Њ–ґ–µ–Љ —Б—З–Є—В–∞—В—М, —З—В–Њ ![]() . –С–Њ–ї–µ–µ —В–Њ–≥–Њ,
—В–∞–Ї –Ї–∞–Ї –і–µ–є—Б—В–≤–Є–µ —Б–Њ–њ—А—П–ґ–µ–љ–Є—П–Љ–Є, —В–Њ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї–∞–≥–∞—В—М –і–∞–ґ–µ, —З—В–Њ
. –С–Њ–ї–µ–µ —В–Њ–≥–Њ,
—В–∞–Ї –Ї–∞–Ї –і–µ–є—Б—В–≤–Є–µ —Б–Њ–њ—А—П–ґ–µ–љ–Є—П–Љ–Є, —В–Њ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї–∞–≥–∞—В—М –і–∞–ґ–µ, —З—В–Њ ![]() .
.
–Я–∞—А–∞
–∞—Д—Д–Є–љ–љ—Л—Е G-–Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–є ![]() (G -
–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–∞—П —А–µ–і—Г–Ї—В–Є–≤–љ–∞—П –≥—А—Г–њ–њ–∞) –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Е–Њ—А–Њ—И–µ–є, –µ—Б–ї–Є K[W] –Є IV - G- –Љ–Њ–і—Г–ї–Є
—Б –•–§. –Ч–і–µ—Б—М IV - —Н—В–Њ –Є–і–µ–∞–ї
(G -
–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–∞—П —А–µ–і—Г–Ї—В–Є–≤–љ–∞—П –≥—А—Г–њ–њ–∞) –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Е–Њ—А–Њ—И–µ–є, –µ—Б–ї–Є K[W] –Є IV - G- –Љ–Њ–і—Г–ї–Є
—Б –•–§. –Ч–і–µ—Б—М IV - —Н—В–Њ –Є–і–µ–∞–ї ![]() . –Я—Г—Б—В—М
W=M(n), V= C(A)=CG(A), –≥–і–µ
. –Я—Г—Б—В—М
W=M(n), V= C(A)=CG(A), –≥–і–µ ![]() . –Э–∞—И–∞ –Ј–∞–і–∞—З–∞
—Б–µ–є—З–∞—Б - –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ
. –Э–∞—И–∞ –Ј–∞–і–∞—З–∞
—Б–µ–є—З–∞—Б - –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ ![]() –Є, —З—В–Њ
–Є, —З—В–Њ ![]() - —Е–Њ—А–Њ—И–∞—П –њ–∞—А–∞.
- —Е–Њ—А–Њ—И–∞—П –њ–∞—А–∞.
–Э–µ—В—А—Г–і–љ–Њ
–њ—А–Њ–≤–µ—А–Є—В—М, —З—В–Њ ¬†g-1Ag = En + (a-1)(xij),
–≥–і–µ xij = g1ig1j, g=(gij), En - –µ–і–Є–љ–Є—З–љ–∞—П –Љ–∞—В—А–Є—Ж–∞. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —З–µ—А–µ–Ј M(n)r
–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –Љ–∞—В—А–Є—Ж —А–∞–љ–≥–∞ ![]() , –∞ —З–µ—А–µ–Ј S -
–њ–Њ–і–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ —Б–Є–Љ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –Љ–∞—В—А–Є—Ж –≤ M(n).
, –∞ —З–µ—А–µ–Ј S -
–њ–Њ–і–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ —Б–Є–Љ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –Љ–∞—В—А–Є—Ж –≤ M(n).
–Ы–µ–Љ–Љ–∞
1. –Ъ–ї–∞—Б—Б —Б–Њ–њ—А—П–ґ–µ–љ–љ–Њ—Б—В–Є V —Б–Њ–≤–њ–∞–і–∞–µ—В —Б ![]() , –≥–і–µ T - —Н—В–Њ
–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –≤—Б–µ—Е –Љ–∞—В—А–Є—Ж, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–Є—Е —Г—Б–ї–Њ–≤–Є—П–Љ
, –≥–і–µ T - —Н—В–Њ
–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –≤—Б–µ—Е –Љ–∞—В—А–Є—Ж, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–Є—Е —Г—Б–ї–Њ–≤–Є—П–Љ ![]() .
.
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ
–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ ![]() —З–µ—А–µ–Ј L
—З–µ—А–µ–Ј L
–Ф–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ.
–Ы–µ–≥–Ї–Њ –њ—А–Њ–≤–µ—А–Є—В—М –љ–µ–њ–Њ—Б—А–µ–і—Б—В–≤–µ–љ–љ–Њ, —З—В–Њ M(n)1 —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ–Љ –Љ–∞—В—А–Є—Ж –≤–Є–і–∞
(xiyj), –≥–і–µ ![]() –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ
–њ—А–Њ–±–µ–≥–∞—О—В –≤—Б–µ –≤–µ–Ї—В–Њ—А—Л –Є–Ј n-–Љ–µ—А–љ–Њ–≥–Њ –≤–µ–Ї—В–Њ—А–љ–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ E(n). –Я—Г—Б—В—М
–љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ
–њ—А–Њ–±–µ–≥–∞—О—В –≤—Б–µ –≤–µ–Ї—В–Њ—А—Л –Є–Ј n-–Љ–µ—А–љ–Њ–≥–Њ –≤–µ–Ї—В–Њ—А–љ–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ E(n). –Я—Г—Б—В—М ![]() –Є –ї–µ–ґ–Є—В –≤
–Є –ї–µ–ґ–Є—В –≤ ![]() . –Ґ–Њ–≥–і–∞ xiyj =
yixj. –Э–∞–є–і—Г—В—Б—П xi0 –Є yj0 –љ–µ —А–∞–≤–љ—Л–µ –љ—Г–ї—О, –≤–µ–і—М
. –Ґ–Њ–≥–і–∞ xiyj =
yixj. –Э–∞–є–і—Г—В—Б—П xi0 –Є yj0 –љ–µ —А–∞–≤–љ—Л–µ –љ—Г–ї—О, –≤–µ–і—М ![]() . –Ґ–Њ–≥–і–∞ –Є–Ј
xi0yj0 = yi0xj0 —Б–ї–µ–і—Г–µ—В, —З—В–Њ
. –Ґ–Њ–≥–і–∞ –Є–Ј
xi0yj0 = yi0xj0 —Б–ї–µ–і—Г–µ—В, —З—В–Њ ![]() . –Ф–∞–ї–µ–µ, –µ—Б–ї–Є
xi =0, —В–Њ–≥–і–∞ xi0yi= yi0xi =0, —В–Њ –µ—Б—В—М yi=0 –Є –љ–∞–Њ–±–Њ—А–Њ—В. –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, xi =0
—В–Њ–≥–і–∞ –Є —В–Њ–ї—М–Ї–Њ —В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ yi =0. –С–Њ–ї–µ–µ —В–Њ–≥–Њ, –і–ї—П –љ–µ–љ—Г–ї–µ–≤—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤
–Њ—В–љ–Њ—И–µ–љ–Є–µ xi/yi —П–≤–ї—П–µ—В—Б—П –Ї–Њ–љ—Б—В–∞–љ—В–Њ–є. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ –µ–µ t. –Я–µ—А–µ—Е–Њ–і—П –Ї –њ–∞—А–∞–Љ–µ—В—А–∞–Љ
xi'=t-1/2xi=yi'=t1/2yi, –Љ–Њ–ґ–љ–Њ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—В—М, —З—В–Њ xi=yi –і–ї—П –≤—Б–µ—Е i. –Я–Њ–і—Б—В–∞–≤–ї—П—П –≤
—Г—А–∞–≤–љ–µ–љ–Є—П –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є–µ T –Є –Є—Б–њ–Њ–ї—М–Ј—Г—П —В–Њ, —З—В–Њ
. –Ф–∞–ї–µ–µ, –µ—Б–ї–Є
xi =0, —В–Њ–≥–і–∞ xi0yi= yi0xi =0, —В–Њ –µ—Б—В—М yi=0 –Є –љ–∞–Њ–±–Њ—А–Њ—В. –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, xi =0
—В–Њ–≥–і–∞ –Є —В–Њ–ї—М–Ї–Њ —В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ yi =0. –С–Њ–ї–µ–µ —В–Њ–≥–Њ, –і–ї—П –љ–µ–љ—Г–ї–µ–≤—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤
–Њ—В–љ–Њ—И–µ–љ–Є–µ xi/yi —П–≤–ї—П–µ—В—Б—П –Ї–Њ–љ—Б—В–∞–љ—В–Њ–є. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ –µ–µ t. –Я–µ—А–µ—Е–Њ–і—П –Ї –њ–∞—А–∞–Љ–µ—В—А–∞–Љ
xi'=t-1/2xi=yi'=t1/2yi, –Љ–Њ–ґ–љ–Њ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—В—М, —З—В–Њ xi=yi –і–ї—П –≤—Б–µ—Е i. –Я–Њ–і—Б—В–∞–≤–ї—П—П –≤
—Г—А–∞–≤–љ–µ–љ–Є—П –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є–µ T –Є –Є—Б–њ–Њ–ї—М–Ј—Г—П —В–Њ, —З—В–Њ ![]() , –Љ—Л –њ–Њ–ї—Г—З–Є–Љ,
—З—В–Њ
, –Љ—Л –њ–Њ–ї—Г—З–Є–Љ,
—З—В–Њ ![]() . –Ф–Њ—Б—В—А–Њ–Є–Љ
c–Є—Б—В–µ–Љ—Г –Є–Ј –Њ–і–љ–Њ–≥–Њ –≤–µ–Ї—В–Њ—А–∞ x –і–Њ –Њ—А—В–Њ–љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ –±–∞–Ј–Є—Б–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ E(n) –Є
—А–∞—Б–њ–Њ–ї–Њ–ґ–Є–Љ –≤–µ–Ї—В–Њ—А—Л —Н—В–Њ–≥–Њ –±–∞–Ј–Є—Б–∞ —Б—В–Њ–ї–±—Ж–∞–Љ–Є (–њ—А–Є—З–µ–Љ x - –њ–µ—А–≤—Л–є) –≤ –Љ–∞—В—А–Є—Ж–µ g.
–ѓ—Б–љ–Њ, —З—В–Њ
. –Ф–Њ—Б—В—А–Њ–Є–Љ
c–Є—Б—В–µ–Љ—Г –Є–Ј –Њ–і–љ–Њ–≥–Њ –≤–µ–Ї—В–Њ—А–∞ x –і–Њ –Њ—А—В–Њ–љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ –±–∞–Ј–Є—Б–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ E(n) –Є
—А–∞—Б–њ–Њ–ї–Њ–ґ–Є–Љ –≤–µ–Ї—В–Њ—А—Л —Н—В–Њ–≥–Њ –±–∞–Ј–Є—Б–∞ —Б—В–Њ–ї–±—Ж–∞–Љ–Є (–њ—А–Є—З–µ–Љ x - –њ–µ—А–≤—Л–є) –≤ –Љ–∞—В—А–Є—Ж–µ g.
–ѓ—Б–љ–Њ, —З—В–Њ ![]() , –Є g-1Ag = En
+ (a-1)z. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ,
, –Є g-1Ag = En
+ (a-1)z. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, ![]() . –Ю–±—А–∞—В–љ–Њ–µ
–≤–Ї–ї—О—З–µ–љ–Є–µ –Њ—З–µ–≤–Є–і–љ–Њ.
. –Ю–±—А–∞—В–љ–Њ–µ
–≤–Ї–ї—О—З–µ–љ–Є–µ –Њ—З–µ–≤–Є–і–љ–Њ.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
![]() , —В–Њ –Љ—Л –Љ–Њ–ґ–µ–Љ
–≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –ї–µ–Љ–Љ–Њ–є 1 (
, —В–Њ –Љ—Л –Љ–Њ–ґ–µ–Љ
–≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –ї–µ–Љ–Љ–Њ–є 1 (![]() ) [7] –Є
–Ј–∞–Ї–ї—О—З–Є—В—М, —З—В–Њ
) [7] –Є
–Ј–∞–Ї–ї—О—З–Є—В—М, —З—В–Њ ![]() , –µ—Б–ї–Є
–і–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ
, –µ—Б–ї–Є
–і–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ ![]() –љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ
–Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ. C–і–≤–Є–≥ –Є —Г–Љ–љ–Њ–ґ–µ–љ–Є–µ –љ–∞ (–љ–µ–љ—Г–ї–µ–≤–Њ–є) —Б–Ї–∞–ї—П—А - –≥–Њ–Љ–µ–Њ–Љ–Њ—А—Д–Є–Ј–Љ—Л, –њ–Њ—Н—В–Њ–Љ—Г
–і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –љ–Њ—А–Љ–∞–ї—М–љ–Њ L. –Я—Г—Б—В—М Sn - –µ–і–Є–љ–Є—З–љ–∞—П —Б—Д–µ—А–∞ –≤ E(n). –Ш–Ј
—Б–Ї–∞–Ј–∞–љ–љ–Њ–≥–Њ –≤—Л—И–µ —П—Б–љ–Њ, —З—В–Њ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ –Є–Ј Sn –≤ L –њ–Њ –њ—А–∞–≤–Є–ї—Г
–љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ
–Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ. C–і–≤–Є–≥ –Є —Г–Љ–љ–Њ–ґ–µ–љ–Є–µ –љ–∞ (–љ–µ–љ—Г–ї–µ–≤–Њ–є) —Б–Ї–∞–ї—П—А - –≥–Њ–Љ–µ–Њ–Љ–Њ—А—Д–Є–Ј–Љ—Л, –њ–Њ—Н—В–Њ–Љ—Г
–і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –љ–Њ—А–Љ–∞–ї—М–љ–Њ L. –Я—Г—Б—В—М Sn - –µ–і–Є–љ–Є—З–љ–∞—П —Б—Д–µ—А–∞ –≤ E(n). –Ш–Ј
—Б–Ї–∞–Ј–∞–љ–љ–Њ–≥–Њ –≤—Л—И–µ —П—Б–љ–Њ, —З—В–Њ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ –Є–Ј Sn –≤ L –њ–Њ –њ—А–∞–≤–Є–ї—Г ![]() —П–≤–ї—П–µ—В—Б—П
–і–Њ–Љ–Є–љ–∞–љ—В–љ—Л–Љ. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, –Љ—Л –Є–Љ–µ–µ–Љ –≤–ї–Њ–ґ–µ–љ–Є–µ
—П–≤–ї—П–µ—В—Б—П
–і–Њ–Љ–Є–љ–∞–љ—В–љ—Л–Љ. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, –Љ—Л –Є–Љ–µ–µ–Љ –≤–ї–Њ–ґ–µ–љ–Є–µ ![]() . –Ю–±—А–∞–Ј —Н—В–Њ–≥–Њ
–≤–ї–Њ–ґ–µ–љ–Є—П –њ–Њ—А–Њ–ґ–і–µ–љ —Н–ї–µ–Љ–µ–љ—В–∞–Љ–Є xixj. –Р–ї–≥–µ–±—А–∞
. –Ю–±—А–∞–Ј —Н—В–Њ–≥–Њ
–≤–ї–Њ–ґ–µ–љ–Є—П –њ–Њ—А–Њ–ґ–і–µ–љ —Н–ї–µ–Љ–µ–љ—В–∞–Љ–Є xixj. –Р–ї–≥–µ–±—А–∞ ![]() –Є–Љ–µ–µ—В
–≥—А–∞–і—Г–Є—А–Њ–≤–Ї—Г
–Є–Љ–µ–µ—В
–≥—А–∞–і—Г–Є—А–Њ–≤–Ї—Г ![]() , –≥–і–µ R0 -
–њ–Њ–і–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ, –љ–∞—В—П–љ—Г—В–Њ–µ –љ–∞ –Љ–Њ–љ–Њ–Љ—Л —З–µ—В–љ–Њ–є —Б—В–µ–њ–µ–љ–Є, –∞ R1 - –љ–µ—З–µ—В–љ–Њ–є. –≠–ї–µ–Љ–µ–љ—В
, –≥–і–µ R0 -
–њ–Њ–і–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ, –љ–∞—В—П–љ—Г—В–Њ–µ –љ–∞ –Љ–Њ–љ–Њ–Љ—Л —З–µ—В–љ–Њ–є —Б—В–µ–њ–µ–љ–Є, –∞ R1 - –љ–µ—З–µ—В–љ–Њ–є. –≠–ї–µ–Љ–µ–љ—В ![]() –Њ–і–љ–Њ—А–Њ–і–µ–љ
–Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Н—В–Њ–є –≥—А–∞–і—Г–Є—А–Њ–≤–Ї–Є, –њ–Њ—Н—В–Њ–Љ—Г
–Њ–і–љ–Њ—А–Њ–і–µ–љ
–Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Н—В–Њ–є –≥—А–∞–і—Г–Є—А–Њ–≤–Ї–Є, –њ–Њ—Н—В–Њ–Љ—Г ![]() "–љ–∞—Б–ї–µ–і—Г–µ—В"
–≥—А–∞–і—Г–Є—А–Њ–≤–Ї—Г R. –С—Г–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–∞—В—М –µ–µ —В–µ–Љ–Є –ґ–µ —Б–Є–Љ–≤–Њ–ї–∞–Љ–Є. –Ч–∞–Љ–µ—В–Є–Љ –µ—Й–µ, —З—В–Њ K[L]=R0.
–†–∞–љ–≥ —П–Ї–Њ–±–Є–∞–љ–∞
"–љ–∞—Б–ї–µ–і—Г–µ—В"
–≥—А–∞–і—Г–Є—А–Њ–≤–Ї—Г R. –С—Г–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–∞—В—М –µ–µ —В–µ–Љ–Є –ґ–µ —Б–Є–Љ–≤–Њ–ї–∞–Љ–Є. –Ч–∞–Љ–µ—В–Є–Љ –µ—Й–µ, —З—В–Њ K[L]=R0.
–†–∞–љ–≥ —П–Ї–Њ–±–Є–∞–љ–∞ ![]() —А–∞–≤–µ–љ 1 –њ–Њ
–Ї—А–∞–є–љ–µ–є –Љ–µ—А–µ –љ–∞
—А–∞–≤–µ–љ 1 –њ–Њ
–Ї—А–∞–є–љ–µ–є –Љ–µ—А–µ –љ–∞ ![]() , –Є
, –Є ![]() . –Я–Њ –Ї—А–Є—В–µ—А–Є—О
–°–µ—А—А–∞ ([6]
. –Я–Њ –Ї—А–Є—В–µ—А–Є—О
–°–µ—А—А–∞ ([6] ![]() , —В–µ–Њ—А–µ–Љ–∞
5.8.6), K[Sn] –љ–Њ—А–Љ–∞–ї—М–љ–Њ (
, —В–µ–Њ—А–µ–Љ–∞
5.8.6), K[Sn] –љ–Њ—А–Љ–∞–ї—М–љ–Њ (![]() ). –Я—Г—Б—В—М
—В–µ–њ–µ—А—М
). –Я—Г—Б—В—М
—В–µ–њ–µ—А—М ![]() - —Ж–µ–ї—Л–є –љ–∞–і
R0. –Ґ–∞–Ї –Ї–∞–Ї
- —Ж–µ–ї—Л–є –љ–∞–і
R0. –Ґ–∞–Ї –Ї–∞–Ї ![]() , —В–Њ
, —В–Њ ![]() –Є
–Є ![]() .
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ,
.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, ![]() , —В–Њ –µ—Б—В—М
, —В–Њ –µ—Б—В—М ![]() , –Њ—В–Ї—Г–і–∞ z1=0.
, –Њ—В–Ї—Г–і–∞ z1=0.
–°–Њ–≥–ї–∞—Б–љ–Њ
–њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—О 6.7 [2], —З—В–Њ–±—Л –і–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ ![]() (
(![]() –Њ—В–Њ–ґ–і–µ—Б—В–≤–ї—П–µ—В—Б—П —Б
–Њ—В–Њ–ґ–і–µ—Б—В–≤–ї—П–µ—В—Б—П —Б ![]() , –≥–і–µ ZG(A) -
—Ж–µ–љ—В—А–∞–ї–Є–Ј–∞—В–Њ—А —Н–ї–µ–Љ–µ–љ—В–∞ A, –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ—А–Њ–≤–µ—А–Є—В—М, —З—В–Њ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї
, –≥–і–µ ZG(A) -
—Ж–µ–љ—В—А–∞–ї–Є–Ј–∞—В–Њ—А —Н–ї–µ–Љ–µ–љ—В–∞ A, –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ—А–Њ–≤–µ—А–Є—В—М, —З—В–Њ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї ![]() —Б—О—А—К–µ–Ї—В–Є–≤–µ–љ.
–Ю–і–љ–∞–Ї–Њ
—Б—О—А—К–µ–Ї—В–Є–≤–µ–љ.
–Ю–і–љ–∞–Ї–Њ ![]() . –Ш—Б–њ–Њ–ї—М–Ј—Г—П
—Д–Њ—А–Љ–∞–ї–Є–Ј–Љ —Б –і–≤–Њ–є–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є [8], –Є–Љ–µ–µ–Љ:
. –Ш—Б–њ–Њ–ї—М–Ј—Г—П
—Д–Њ—А–Љ–∞–ї–Є–Ј–Љ —Б –і–≤–Њ–є–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є [8], –Є–Љ–µ–µ–Љ: ![]() . –Ґ–∞–Ї–Є–Љ
–Њ–±—А–∞–Ј–Њ–Љ,
. –Ґ–∞–Ї–Є–Љ
–Њ–±—А–∞–Ј–Њ–Љ, ![]() . –Ю—В—Б—О–і–∞ —П—Б–љ–Њ,
—З—В–Њ –Њ–±—А–∞–Ј
. –Ю—В—Б—О–і–∞ —П—Б–љ–Њ,
—З—В–Њ –Њ–±—А–∞–Ј ![]() –Є–Љ–µ–µ—В —В—Г –ґ–µ
—А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М n-1. –Ш—В–∞–Ї,
–Є–Љ–µ–µ—В —В—Г –ґ–µ
—А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М n-1. –Ш—В–∞–Ї, ![]() . –Ю—В–Љ–µ—В–Є–Љ –µ—Й–µ
–і–ї—П –і–∞–ї—М–љ–µ–є—И–µ–≥–Њ, —З—В–Њ ZG(A) —Б–Њ—Б—В–Њ–Є—В –Є–Ј –Љ–∞—В—А–Є—Ж, —Г –Ї–Њ—В–Њ—А—Л—Е –њ—А–∞–≤—Л–є
"–љ–Є–ґ–љ–Є–є"
. –Ю—В–Љ–µ—В–Є–Љ –µ—Й–µ
–і–ї—П –і–∞–ї—М–љ–µ–є—И–µ–≥–Њ, —З—В–Њ ZG(A) —Б–Њ—Б—В–Њ–Є—В –Є–Ј –Љ–∞—В—А–Є—Ж, —Г –Ї–Њ—В–Њ—А—Л—Е –њ—А–∞–≤—Л–є
"–љ–Є–ґ–љ–Є–є" ![]() -—Г–≥–Њ–ї - —Н—В–Њ
–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–∞—П –Љ–∞—В—А–Є—Ж–∞ –Є–Ј G(n-1), –∞ –≤ –њ–µ—А–≤–Њ–Љ —Б—В–Њ–ї–±—Ж–µ –Є –њ–µ—А–≤–Њ–є —Б—В—А–Њ–Ї–µ –≤–µ–Ј–і–µ —Б—В–Њ—П—В
–љ—Г–ї–Є, –Ї—А–Њ–Љ–µ –љ–∞—З–∞–ї–∞, –≥–і–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В —А–∞–≤–µ–љ
-—Г–≥–Њ–ї - —Н—В–Њ
–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–∞—П –Љ–∞—В—А–Є—Ж–∞ –Є–Ј G(n-1), –∞ –≤ –њ–µ—А–≤–Њ–Љ —Б—В–Њ–ї–±—Ж–µ –Є –њ–µ—А–≤–Њ–є —Б—В—А–Њ–Ї–µ –≤–µ–Ј–і–µ —Б—В–Њ—П—В
–љ—Г–ї–Є, –Ї—А–Њ–Љ–µ –љ–∞—З–∞–ї–∞, –≥–і–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В —А–∞–≤–µ–љ ![]() .
.
–Я–Њ
—В–µ–Љ –ґ–µ —Б–Њ–Њ–±—А–∞–ґ–µ–љ–Є—П–Љ, —З—В–Њ –Є –≤—Л—И–µ, –Њ—Б—В–∞–ї–Њ—Б—М –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ (M(n), L) - —Е–Њ—А–Њ—И–∞—П
–њ–∞—А–∞. –°–Њ–≥–ї–∞—Б–љ–Њ –ї–µ–Љ–Љ–µ 1.3(a) [4], –Љ–Њ–ґ–љ–Њ —А–∞—Б—Б–Љ–Њ—В—А–µ—В—М "–±–∞—И–љ—О" ![]() –Є –њ—А–Њ–≤–µ—А–Є—В—М
–Ї–∞–ґ–і—Л–є "—Б–Ї–∞—З–Њ–Ї". –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–љ–∞—З–∞–ї–∞
–Є –њ—А–Њ–≤–µ—А–Є—В—М
–Ї–∞–ґ–і—Л–є "—Б–Ї–∞—З–Њ–Ї". –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–љ–∞—З–∞–ї–∞ ![]() . –Ь—Л –Є–Љ–µ–µ–Љ
–Ї–Њ–Љ–Љ—Г—В–∞—В–Є–≤–љ—Г—О (–≤—Б–µ –Љ–Њ—А—Д–Є–Ј–Љ—Л G-—Н–Ї–≤–Є–≤–∞—А–Є–∞–љ—В–љ—Л) –і–Є–∞–≥—А–∞–Љ–Љ—Г:
. –Ь—Л –Є–Љ–µ–µ–Љ
–Ї–Њ–Љ–Љ—Г—В–∞—В–Є–≤–љ—Г—О (–≤—Б–µ –Љ–Њ—А—Д–Є–Ј–Љ—Л G-—Н–Ї–≤–Є–≤–∞—А–Є–∞–љ—В–љ—Л) –і–Є–∞–≥—А–∞–Љ–Љ—Г:
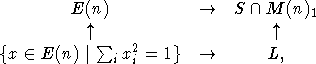 ¬†–≥–і–µ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–µ —Б—В—А–µ–ї–Ї–Є - —Н—В–Њ –њ—А–Њ—Б—В–Њ
–≤–Ї–ї—О—З–µ–љ–Є—П. –Я–µ—А–µ—Е–Њ–і—П –Ї –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–Љ –∞–ї–≥–µ–±—А–∞–Љ, –Љ—Л –њ–Њ–ї—Г—З–Є–Љ "–і—Г–∞–ї—М–љ—Г—О"
–і–Є–∞–≥—А–∞–Љ–Љ—Г:
¬†–≥–і–µ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–µ —Б—В—А–µ–ї–Ї–Є - —Н—В–Њ –њ—А–Њ—Б—В–Њ
–≤–Ї–ї—О—З–µ–љ–Є—П. –Я–µ—А–µ—Е–Њ–і—П –Ї –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–Љ –∞–ї–≥–µ–±—А–∞–Љ, –Љ—Л –њ–Њ–ї—Г—З–Є–Љ "–і—Г–∞–ї—М–љ—Г—О"
–і–Є–∞–≥—А–∞–Љ–Љ—Г:
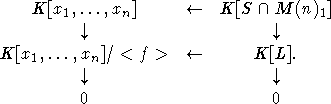
–Т
–њ–µ—А–≤–Њ–є –і–Є–∞–≥—А–∞–Љ–Љ–µ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л–µ —Б—В—А–µ–ї–Ї–Є - G-–і–Њ–Љ–Є–љ–∞–љ—В–љ—Л–µ –Љ–Њ—А—Д–Є–Ј–Љ—Л, –њ–Њ—Н—В–Њ–Љ—Г –≤–Њ –≤—В–Њ—А–Њ–є
- –≤–ї–Њ–ґ–µ–љ–Є—П. –Ю—В—Б—О–і–∞ —П—Б–љ–Њ, —З—В–Њ ![]() –Љ–Њ–ґ–љ–Њ
–Њ—В–Њ–ґ–і–µ—Б—В–≤–Є—В—М —Б
–Љ–Њ–ґ–љ–Њ
–Њ—В–Њ–ґ–і–µ—Б—В–≤–Є—В—М —Б ![]() (–≤ –њ—А–Є–љ—П—В—Л—Е
–≤—Л—И–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П—Е). –Ч–і–µ—Б—М I - –Є–і–µ–∞–ї, –њ–Њ—А–Њ–ґ–і–µ–љ–љ—Л–є —Н–ї–µ–Љ–µ–љ—В–Њ–Љ f. –Ш–Ј —В–µ—Е –ґ–µ
–≥—А–∞–і—Г–Є—А–Њ–≤–Њ—З–љ—Л—Е —Б–Њ–Њ–±—А–∞–ґ–µ–љ–Є–є —П—Б–љ–Њ, —З—В–Њ
(–≤ –њ—А–Є–љ—П—В—Л—Е
–≤—Л—И–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П—Е). –Ч–і–µ—Б—М I - –Є–і–µ–∞–ї, –њ–Њ—А–Њ–ґ–і–µ–љ–љ—Л–є —Н–ї–µ–Љ–µ–љ—В–Њ–Љ f. –Ш–Ј —В–µ—Е –ґ–µ
–≥—А–∞–і—Г–Є—А–Њ–≤–Њ—З–љ—Л—Е —Б–Њ–Њ–±—А–∞–ґ–µ–љ–Є–є —П—Б–љ–Њ, —З—В–Њ ![]() . –Ю—Б—В–∞–ї–Њ—Б—М
–Њ—В–Љ–µ—В–Є—В—М, —З—В–Њ f G-–Є–љ–≤–∞—А–Є–∞–љ—В –Є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, G-–Љ–Њ–і—Г–ї—М
. –Ю—Б—В–∞–ї–Њ—Б—М
–Њ—В–Љ–µ—В–Є—В—М, —З—В–Њ f G-–Є–љ–≤–∞—А–Є–∞–љ—В –Є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, G-–Љ–Њ–і—Г–ї—М ![]() –Є–Ј–Њ–Љ–Њ—А—Д–µ–љ R0.
–Ґ–Њ, —З—В–Њ R0 —Б –•–§, –±—Г–і–µ—В —Б–ї–µ–і–Њ–≤–∞—В—М –Є–Ј —В–Њ–≥–Њ, —З—В–Њ
–Є–Ј–Њ–Љ–Њ—А—Д–µ–љ R0.
–Ґ–Њ, —З—В–Њ R0 —Б –•–§, –±—Г–і–µ—В —Б–ї–µ–і–Њ–≤–∞—В—М –Є–Ј —В–Њ–≥–Њ, —З—В–Њ ![]() - —Е–Њ—А–Њ—И–∞—П
–њ–∞—А–∞.
- —Е–Њ—А–Њ—И–∞—П
–њ–∞—А–∞.
–Я—Г—Б—В—М
—В–µ–њ–µ—А—М ![]() –њ–Њ –њ—А–∞–≤–Є–ї—Г
–њ–Њ –њ—А–∞–≤–Є–ї—Г ![]() . –ѓ—Б–љ–Њ, —З—В–Њ
. –ѓ—Б–љ–Њ, —З—В–Њ ![]() -—Н–Ї–≤–Є–≤–∞—А–Є–∞–љ—В–љ–Њ–µ
–Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ, –≥–і–µ K* = GL(1) –і–µ–є—Б—В–≤—Г–µ—В –њ–Њ –њ—А–∞–≤–Є–ї—Г
-—Н–Ї–≤–Є–≤–∞—А–Є–∞–љ—В–љ–Њ–µ
–Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ, –≥–і–µ K* = GL(1) –і–µ–є—Б—В–≤—Г–µ—В –њ–Њ –њ—А–∞–≤–Є–ї—Г ![]() . –Э–∞–њ–Њ–Љ–љ–Є–Љ,
—З—В–Њ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ G-–Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–є
. –Э–∞–њ–Њ–Љ–љ–Є–Љ,
—З—В–Њ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ G-–Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–є ![]() –љ–∞–Ј—Л–≤–∞–µ—В—Б—П
—Д–∞–Ї—В–Њ—А–љ—Л–Љ, –µ—Б–ї–Є
–љ–∞–Ј—Л–≤–∞–µ—В—Б—П
—Д–∞–Ї—В–Њ—А–љ—Л–Љ, –µ—Б–ї–Є ![]() —Б—О—А—К–µ–Ї—В–Є–≤–љ–Њ –Є
—Б—О—А—К–µ–Ї—В–Є–≤–љ–Њ –Є ![]() . –•–Њ—А–Њ—И–Њ
–Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ
. –•–Њ—А–Њ—И–Њ
–Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ ![]() K*-—Д–∞–Ї—В–Њ—А–љ–Њ–µ
–Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ [4]. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —З–µ—А–µ–Ј
K*-—Д–∞–Ї—В–Њ—А–љ–Њ–µ
–Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ [4]. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —З–µ—А–µ–Ј ![]() . –Я–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ
(U, B) - —Е–Њ—А–Њ—И–∞—П –њ–∞—А–∞. –§—Г–љ–Ї—В–Њ—А –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П –њ–µ—А–µ–≤–Њ–і–Є—В GL(n)-–Љ–Њ–і—Г–ї–Є —Б –•–§ –≤
G-–Љ–Њ–і—Г–ї–Є —Б –•–§. –Р–ї–≥–µ–±—А–∞
. –Я–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ
(U, B) - —Е–Њ—А–Њ—И–∞—П –њ–∞—А–∞. –§—Г–љ–Ї—В–Њ—А –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П –њ–µ—А–µ–≤–Њ–і–Є—В GL(n)-–Љ–Њ–і—Г–ї–Є —Б –•–§ –≤
G-–Љ–Њ–і—Г–ї–Є —Б –•–§. –Р–ї–≥–µ–±—А–∞ ![]() –Є–Ј–Њ–Љ–Њ—А—Д–љ–∞
–Є–Ј–Њ–Љ–Њ—А—Д–љ–∞ ![]() –Ї–∞–Ї
–Ї–∞–Ї ![]() -–Љ–Њ–і—Г–ї—М (Kl -
—Н—В–Њ –Њ–і–љ–Њ–Љ–µ—А–љ—Л–є K*-–Љ–Њ–і—Г–ї—М —Б –≤–µ—Б–Њ–Љ l). –•–Њ—А–Њ—И–Њ –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ GL(n)-–Љ–Њ–і—Г–ї—М Sk(E(n))
—Б –•–§ [9]. –Я–Њ —В–µ–Њ—А–µ–Љ–µ –Ф–Њ–љ–Ї–Є–љ–∞-–Ь–∞—В—М–µ, K[U]
-–Љ–Њ–і—Г–ї—М (Kl -
—Н—В–Њ –Њ–і–љ–Њ–Љ–µ—А–љ—Л–є K*-–Љ–Њ–і—Г–ї—М —Б –≤–µ—Б–Њ–Љ l). –•–Њ—А–Њ—И–Њ –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ GL(n)-–Љ–Њ–і—Г–ї—М Sk(E(n))
—Б –•–§ [9]. –Я–Њ —В–µ–Њ—А–µ–Љ–µ –Ф–Њ–љ–Ї–Є–љ–∞-–Ь–∞—В—М–µ, K[U] ![]() -–Љ–Њ–і—Г–ї—М —Б –•–§.
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –і–Њ–Ї–∞–Ј—Л–≤–∞—В—М –љ–∞–ї–Є—З–Є–µ –•–§ —В–Њ–ї—М–Ї–Њ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ G. –Я—А–µ–і—Б—В–∞–≤–Є–Љ
–∞–ї–≥–µ–±—А—Г K[U] –≤ –≤–Є–і–µ
-–Љ–Њ–і—Г–ї—М —Б –•–§.
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –і–Њ–Ї–∞–Ј—Л–≤–∞—В—М –љ–∞–ї–Є—З–Є–µ –•–§ —В–Њ–ї—М–Ї–Њ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ G. –Я—А–µ–і—Б—В–∞–≤–Є–Љ
–∞–ї–≥–µ–±—А—Г K[U] –≤ –≤–Є–і–µ ![]() .
–Ю—В–Њ–ґ–і–µ—Б—В–≤–ї–µ–љ–Є–µ –њ—А–Њ–Є—Б—Е–Њ–і–Є—В –њ–Њ –њ—А–∞–≤–Є–ї—Г
.
–Ю—В–Њ–ґ–і–µ—Б—В–≤–ї–µ–љ–Є–µ –њ—А–Њ–Є—Б—Е–Њ–і–Є—В –њ–Њ –њ—А–∞–≤–Є–ї—Г ![]() , –≥–і–µ
, –≥–і–µ ![]() - —Б—В–∞–љ–і–∞—А—В–љ—Л–є
–±–∞–Ј–Є—Б E(n), –∞ f1,f2 - E(2). C–Њ–≥–ї–∞—Б–љ–Њ [1],
- —Б—В–∞–љ–і–∞—А—В–љ—Л–є
–±–∞–Ј–Є—Б E(n), –∞ f1,f2 - E(2). C–Њ–≥–ї–∞—Б–љ–Њ [1], ![]() –Є–Љ–µ–µ—В
–Є–Љ–µ–µ—В ![]() -—Д–Є–ї—М—В—А–∞—Ж–Є—О c
—Д–∞–Ї—В–Њ—А–∞–Љ–Є
-—Д–Є–ї—М—В—А–∞—Ж–Є—О c
—Д–∞–Ї—В–Њ—А–∞–Љ–Є ![]() , –≥–і–µ
, –≥–і–µ ![]() - —Д—Г–љ–Ї—В–Њ—А
–®—Г—А–∞,
- —Д—Г–љ–Ї—В–Њ—А
–®—Г—А–∞, ![]() –њ—А–Њ–±–µ–≥–∞–µ—В –≤—Б–µ
—А–∞–Ј–±–Є–µ–љ–Є—П —Б
–њ—А–Њ–±–µ–≥–∞–µ—В –≤—Б–µ
—А–∞–Ј–±–Є–µ–љ–Є—П —Б ![]() . –Э–µ—В—А—Г–і–љ–Њ
–Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –Є–і–µ–∞–ї, –њ–Њ—А–Њ–ґ–і–µ–љ–љ—Л–є xiyj-xjyi, —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —В–Њ–є —З–∞—Б—В—М—О —Д–Є–ї—М—В—А–∞—Ж–Є–Є,
–≥–і–µ
. –Э–µ—В—А—Г–і–љ–Њ
–Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –Є–і–µ–∞–ї, –њ–Њ—А–Њ–ґ–і–µ–љ–љ—Л–є xiyj-xjyi, —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —В–Њ–є —З–∞—Б—В—М—О —Д–Є–ї—М—В—А–∞—Ж–Є–Є,
–≥–і–µ ![]() . –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г ![]() –±–µ–Ј –Ї—А—Г—З–µ–љ–Є—П
[3], —В–Њ
–±–µ–Ј –Ї—А—Г—З–µ–љ–Є—П
[3], —В–Њ ![]() . –Т —З–∞—Б—В–љ–Њ—Б—В–Є,
IB —Б –•–§ –Ї–∞–Ї G-–Љ–Њ–і—Г–ї—М, –∞ –Ј–љ–∞—З–Є—В, –Є –Ї–∞–Ї
. –Т —З–∞—Б—В–љ–Њ—Б—В–Є,
IB —Б –•–§ –Ї–∞–Ї G-–Љ–Њ–і—Г–ї—М, –∞ –Ј–љ–∞—З–Є—В, –Є –Ї–∞–Ї ![]() -–Љ–Њ–і—Г–ї—М. –Т
–Є—В–Њ–≥–µ –Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є—П U, B, Z —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—В —Г—Б–ї–Њ–≤–Є—П–Љ –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П 1.4(a) –Є–Ј [4]. –Р
—Н—В–Њ –Ј–љ–∞—З–Є—В –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, —З—В–Њ
-–Љ–Њ–і—Г–ї—М. –Т
–Є—В–Њ–≥–µ –Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є—П U, B, Z —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—В —Г—Б–ї–Њ–≤–Є—П–Љ –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П 1.4(a) –Є–Ј [4]. –Р
—Н—В–Њ –Ј–љ–∞—З–Є—В –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, —З—В–Њ ![]() - —Е–Њ—А–Њ—И–∞—П
–њ–∞—А–∞. –Ю—Б—В–∞–ї–Њ—Б—М –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ (M(n), M(n)1) - —Е–Њ—А–Њ—И–∞—П GL(n)-–њ–∞—А–∞ –њ–Њ [4].
–°–Њ–≥–ї–∞—Б–љ–Њ —Б–Ї–∞–Ј–∞–љ–љ–Њ–Љ—Г –≤—Л—И–µ, —Н—В–Њ —В–∞–Ї–ґ–µ —Е–Њ—А–Њ—И–∞—П G-–њ–∞—А–∞. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, —Е–Њ—А–Њ—И–µ–є
G-–њ–∞—А–Њ–є –±—Г–і–µ—В
- —Е–Њ—А–Њ—И–∞—П
–њ–∞—А–∞. –Ю—Б—В–∞–ї–Њ—Б—М –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ (M(n), M(n)1) - —Е–Њ—А–Њ—И–∞—П GL(n)-–њ–∞—А–∞ –њ–Њ [4].
–°–Њ–≥–ї–∞—Б–љ–Њ —Б–Ї–∞–Ј–∞–љ–љ–Њ–Љ—Г –≤—Л—И–µ, —Н—В–Њ —В–∞–Ї–ґ–µ —Е–Њ—А–Њ—И–∞—П G-–њ–∞—А–∞. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, —Е–Њ—А–Њ—И–µ–є
G-–њ–∞—А–Њ–є –±—Г–і–µ—В ![]() , —З—В–Њ –Є
—В—А–µ–±—Г–µ—В—Б—П.
, —З—В–Њ –Є
—В—А–µ–±—Г–µ—В—Б—П.
–°–ї—Г—З–∞–є
C. –Ч–і–µ—Б—М –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ–Љ—Г —Б–ї—Г—З–∞—О. –Ь—Л —В–Њ–ї—М–Ї–Њ –≤–Ї—А–∞—В—Ж–µ
–њ–Њ–≤—В–Њ—А–Є–Љ –Њ—Б–љ–Њ–≤–љ—Л–µ –Љ–Њ–Љ–µ–љ—В—Л, —Г–Ї–∞–Ј–∞–≤ –Њ—В–ї–Є—З–Є–µ –Њ—В —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–љ–Њ–≥–Њ –≤—Л—И–µ. –Ь–∞—В—А–Є—Ж–∞ A
–Њ—Б—В–∞–µ—В—Б—П —В–Њ–є –ґ–µ —Б–∞–Љ–Њ–є. –Я—А–Є —Н—В–Њ–Љ —Г —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –≥—А—Г–њ–њ—Л ZG(A) –њ–µ—А–≤—Л–µ –Є –њ–Њ—Б–ї–µ–і–љ–Є–µ
—Б—В—А–Њ–Ї–Є –Є —Б—В–Њ–ї–±—Ж—Л –љ—Г–ї–µ–≤—Л–µ, –Ї—А–Њ–Љ–µ —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –љ–∞ –і–Є–∞–≥–Њ–љ–∞–ї–Є, –Ї–Њ—В–Њ—А—Л–µ –≤–Ј–∞–Є–Љ–љ–Њ –Њ–±—А–∞—В–љ—Л
–Є –њ—А–Њ–±–µ–≥–∞—О—В K*. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, "—Б–µ—А–µ–і–Є–љ–љ—Л–є" ![]() -–Ї–≤–∞–і—А–∞—В –ї–µ–ґ–Є—В
–≤ G(n-2)=Spn-2(K). –Ф–∞–ї–µ–µ, –ї–µ–≥–Ї–Њ –њ—А–Њ–≤–µ—А–Є—В—М, —З—В–Њ –Ї–ї–∞—Б—Б —Б–Њ–њ—А—П–ґ–µ–љ–љ–Њ—Б—В–Є C(A)
—Б–Њ–≤–њ–∞–і–∞–µ—В —Б En + (a-1)L, –≥–і–µ
-–Ї–≤–∞–і—А–∞—В –ї–µ–ґ–Є—В
–≤ G(n-2)=Spn-2(K). –Ф–∞–ї–µ–µ, –ї–µ–≥–Ї–Њ –њ—А–Њ–≤–µ—А–Є—В—М, —З—В–Њ –Ї–ї–∞—Б—Б —Б–Њ–њ—А—П–ґ–µ–љ–љ–Њ—Б—В–Є C(A)
—Б–Њ–≤–њ–∞–і–∞–µ—В —Б En + (a-1)L, –≥–і–µ ![]() . –Т —З–∞—Б—В–љ–Њ—Б—В–Є,
–Њ–љ —Г–ґ–µ –Ј–∞–Љ–Ї–љ—Г—В. –Я—А–Њ–≤–µ—А–Ї–∞ —В–Њ–≥–Њ, —З—В–Њ
. –Т —З–∞—Б—В–љ–Њ—Б—В–Є,
–Њ–љ —Г–ґ–µ –Ј–∞–Љ–Ї–љ—Г—В. –Я—А–Њ–≤–µ—А–Ї–∞ —В–Њ–≥–Њ, —З—В–Њ ![]() –Њ—В–Њ–ґ–і–µ—Б—В–≤–ї—П–µ—В—Б—П
—Б —Д–∞–Ї—В–Њ—А–љ—Л–Љ
–Њ—В–Њ–ґ–і–µ—Б—В–≤–ї—П–µ—В—Б—П
—Б —Д–∞–Ї—В–Њ—А–љ—Л–Љ ![]() —Б–Њ–≤–µ—А—И–µ–љ–љ–Њ
–∞–љ–∞–ї–Њ–≥–Є—З–љ–∞. –Ч–і–µ—Б—М
—Б–Њ–≤–µ—А—И–µ–љ–љ–Њ
–∞–љ–∞–ї–Њ–≥–Є—З–љ–∞. –Ч–і–µ—Б—М ![]() , –Њ–±—А–∞–Ј Lie(G)
—Б–Њ—Б—В–Њ–Є—В –Є–Ј –Љ–∞—В—А–Є—Ж —В–Њ–≥–Њ –ґ–µ –≤–Є–і–∞, —З—В–Њ –Є –≤ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ–Љ —Б–ї—Г—З–∞–µ, —В–Њ–ї—М–Ї–Њ
–Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –њ–µ—А–≤–Њ–є —Б—В—А–Њ–Ї–Є –Є –њ–µ—А–≤–Њ–≥–Њ —Б—В–Њ–ї–±—Ж–∞ –љ–Є–Ї–∞–Ї –љ–µ —Б–≤—П–Ј–∞–љ—Л –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ –Є
–њ–Њ—Н—В–Њ–Љ—Г —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М –Њ–±—А–∞–Ј–∞ —В–Њ–ґ–µ —А–∞–≤–љ–∞ 2n-2. –Э–∞–Ї–Њ–љ–µ—Ж, (M(n), L) - –Њ—З–µ–≤–Є–і–љ–Њ
—Е–Њ—А–Њ—И–∞—П –њ–∞—А–∞. –Ф–Њ—Б—В–∞—В–Њ—З–љ–Њ —А–∞—Б—Б–Љ–Њ—В—А–µ—В—М –±–∞—И–љ—О
, –Њ–±—А–∞–Ј Lie(G)
—Б–Њ—Б—В–Њ–Є—В –Є–Ј –Љ–∞—В—А–Є—Ж —В–Њ–≥–Њ –ґ–µ –≤–Є–і–∞, —З—В–Њ –Є –≤ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ–Љ —Б–ї—Г—З–∞–µ, —В–Њ–ї—М–Ї–Њ
–Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –њ–µ—А–≤–Њ–є —Б—В—А–Њ–Ї–Є –Є –њ–µ—А–≤–Њ–≥–Њ —Б—В–Њ–ї–±—Ж–∞ –љ–Є–Ї–∞–Ї –љ–µ —Б–≤—П–Ј–∞–љ—Л –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ –Є
–њ–Њ—Н—В–Њ–Љ—Г —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М –Њ–±—А–∞–Ј–∞ —В–Њ–ґ–µ —А–∞–≤–љ–∞ 2n-2. –Э–∞–Ї–Њ–љ–µ—Ж, (M(n), L) - –Њ—З–µ–≤–Є–і–љ–Њ
—Е–Њ—А–Њ—И–∞—П –њ–∞—А–∞. –Ф–Њ—Б—В–∞—В–Њ—З–љ–Њ —А–∞—Б—Б–Љ–Њ—В—А–µ—В—М –±–∞—И–љ—О ![]() –Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М
—В–Њ, —З—В–Њ tr(x)-1 - G-–Є–љ–≤–∞—А–Є–∞–љ—В! –Ч–∞–Љ–µ—В–Є–Љ –µ—Й–µ, —З—В–Њ –≤ —Б–Є–Љ–њ–ї–µ–Ї—В–Є—З–µ—Б–Ї–Њ–Љ —Б–ї—Г—З–∞–µ
—Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ –њ–Њ–ї—П –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–∞.
–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М
—В–Њ, —З—В–Њ tr(x)-1 - G-–Є–љ–≤–∞—А–Є–∞–љ—В! –Ч–∞–Љ–µ—В–Є–Љ –µ—Й–µ, —З—В–Њ –≤ —Б–Є–Љ–њ–ї–µ–Ї—В–Є—З–µ—Б–Ї–Њ–Љ —Б–ї—Г—З–∞–µ
—Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ –њ–Њ–ї—П –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–∞.
–Я—Г—Б—В—М
—В–µ–њ–µ—А—М G - –ї—О–±–∞—П –≥—А—Г–њ–њ–∞ —В–Є–њ–∞ B, D, C. –Ф–Њ—Б–ї–Њ–≤–љ–Њ –њ–Њ–≤—В–Њ—А—П—П –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ —В–µ–Њ—А–µ–Љ—Л
2 –Є–Ј [5], –Љ—Л –њ–Њ–ї—Г—З–Є–Љ —Н–њ–Є–Љ–Њ—А—Д–Є–Ј–Љ ![]() ,
–Є–љ–і—Г—Ж–Є—А–Њ–≤–∞–љ–љ—Л–є
,
–Є–љ–і—Г—Ж–Є—А–Њ–≤–∞–љ–љ—Л–є ![]() (–љ–∞ –Њ—Б—В–∞–ї—М–љ—Л—Е
–Њ–±—Й–Є—Е –Љ–∞—В—А–Є—Ж–∞—Е –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ —В–Њ–ґ–і–µ—Б—В–≤–µ–љ–љ–Њ). –†–∞–Ј–±–Є–≤ –Љ–∞—В—А–Є—Ж—Л –Є–Ј M(n) –љ–∞ –±–ї–Њ–Ї–Є –≤
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–Є —Б –±–ї–Њ—З–љ—Л–Љ "—Б—В—А–Њ–µ–љ–Є–µ–Љ" –≥—А—Г–њ–њ—Л ZG(A), –Љ—Л –≤–Є–і–Є–Љ, —З—В–Њ
–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ M(n) –Є–Ј–Њ–Љ–Њ—А—Д–љ–Њ (—В–∞–Ї –Ї–∞–Ї ZG(A)-–Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ)
(–љ–∞ –Њ—Б—В–∞–ї—М–љ—Л—Е
–Њ–±—Й–Є—Е –Љ–∞—В—А–Є—Ж–∞—Е –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ —В–Њ–ґ–і–µ—Б—В–≤–µ–љ–љ–Њ). –†–∞–Ј–±–Є–≤ –Љ–∞—В—А–Є—Ж—Л –Є–Ј M(n) –љ–∞ –±–ї–Њ–Ї–Є –≤
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–Є —Б –±–ї–Њ—З–љ—Л–Љ "—Б—В—А–Њ–µ–љ–Є–µ–Љ" –≥—А—Г–њ–њ—Л ZG(A), –Љ—Л –≤–Є–і–Є–Љ, —З—В–Њ
–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ M(n) –Є–Ј–Њ–Љ–Њ—А—Д–љ–Њ (—В–∞–Ї –Ї–∞–Ї ZG(A)-–Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ) ![]() –≤
–Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ–Љ —Б–ї—Г—З–∞–µ –Є
–≤
–Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ–Љ —Б–ї—Г—З–∞–µ –Є ![]() –≤
—Б–Є–Љ–њ–ї–µ–Ї—В–Є—З–µ—Б–Ї–Њ–Љ. –Ч–і–µ—Б—М K –Є K4 —В—А–Є–≤–Є–∞–ї—М–љ—Л–µ –Љ–Њ–і—Г–ї–Є, –∞ –љ–∞ En-1 (—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –љ–∞
En-2) ZG(A) –і–µ–є—Б—В–≤—Г–µ—В –Ї–∞–Ї G(n-1) (G(n-2)) c —В–Њ—З–љ–Њ—Б—В—М—О –і–Њ —Г–Љ–љ–Њ–ґ–µ–љ–Є—П –љ–∞ —Б–Ї–∞–ї—П—А.
–Ю—В—Б—О–і–∞ —П—Б–љ–Њ, —З—В–Њ –Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ
–≤
—Б–Є–Љ–њ–ї–µ–Ї—В–Є—З–µ—Б–Ї–Њ–Љ. –Ч–і–µ—Б—М K –Є K4 —В—А–Є–≤–Є–∞–ї—М–љ—Л–µ –Љ–Њ–і—Г–ї–Є, –∞ –љ–∞ En-1 (—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –љ–∞
En-2) ZG(A) –і–µ–є—Б—В–≤—Г–µ—В –Ї–∞–Ї G(n-1) (G(n-2)) c —В–Њ—З–љ–Њ—Б—В—М—О –і–Њ —Г–Љ–љ–Њ–ґ–µ–љ–Є—П –љ–∞ —Б–Ї–∞–ї—П—А.
–Ю—В—Б—О–і–∞ —П—Б–љ–Њ, —З—В–Њ –Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ ![]() (
(![]() ), –і–∞—Б—В
—Н–њ–Є–Љ–Њ—А—Д–Є–Ј–Љ
), –і–∞—Б—В
—Н–њ–Є–Љ–Њ—А—Д–Є–Ј–Љ ![]() (
(![]() ). –Я—Г—Б—В—М Rn,m
- Q-–∞–ї–≥–µ–±—А–∞, –њ–Њ—А–Њ–ґ–і–µ–љ–љ–∞—П —Б–ї–µ–і–∞–Љ–Є –Њ—В –≤—Б–µ–≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–є –Њ–±—Й–Є—Е –Љ–∞—В—А–Є—Ж, –Є–ї–Є
—В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–љ—Л—Е –Ї –љ–Є–Љ (–≤ —Б–ї—Г—З–∞–µ C - —Б–Є–Љ–њ–ї–µ–Ї—В–Є—З–µ—Б–Ї–Є —В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–љ—Л—Е).
). –Я—Г—Б—В—М Rn,m
- Q-–∞–ї–≥–µ–±—А–∞, –њ–Њ—А–Њ–ґ–і–µ–љ–љ–∞—П —Б–ї–µ–і–∞–Љ–Є –Њ—В –≤—Б–µ–≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–є –Њ–±—Й–Є—Е –Љ–∞—В—А–Є—Ж, –Є–ї–Є
—В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–љ—Л—Е –Ї –љ–Є–Љ (–≤ —Б–ї—Г—З–∞–µ C - —Б–Є–Љ–њ–ї–µ–Ї—В–Є—З–µ—Б–Ї–Є —В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–љ—Л—Е).
–Ы–µ–Љ–Љ–∞
2. –°—Г–њ–µ—А–њ–Њ–Ј–Є—Ж–Є—П –Њ–њ–Є—Б–∞–љ–љ—Л—Е –≤—Л—И–µ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–є - —Н—В–Њ –њ—А–Њ—Б—В–Њ ![]() –Є –Ј–∞—В–µ–Љ -
–Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ –љ–∞ –Њ—Б—В–∞–ї—М–љ—Л—Е –Љ–∞—В—А–Є—Ж–∞—Е.
–Є –Ј–∞—В–µ–Љ -
–Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ –љ–∞ –Њ—Б—В–∞–ї—М–љ—Л—Е –Љ–∞—В—А–Є—Ж–∞—Е.
–Ф–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ.
–Ъ —Б–Њ–ґ–∞–ї–µ–љ–Є—О, —А–∞–Ј–Љ–µ—А—Л —Б—В–∞—В—М–Є, –і–Њ–њ—Г—Б—В–Є–Љ—Л–µ –≤ –і–∞–љ–љ–Њ–Љ –ґ—Г—А–љ–∞–ї–µ, –љ–µ –њ–Њ–Ј–≤–Њ–ї—П—О—В –љ–∞–Љ
–њ—А–Є–≤–µ—Б—В–Є –њ–Њ–ї–љ–Њ–µ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ. –Я–Њ—Н—В–Њ–Љ—Г –Љ—Л –њ—А–Њ—Б—В–Њ –Њ—В–Љ–µ—В–Є–Љ –Ј–і–µ—Б—М, —З—В–Њ In,m
–њ–Њ—А–Њ–ґ–і–∞–µ—В—Б—П —Н–ї–µ–Љ–µ–љ—В–∞–Љ–Є –Є–Ј ![]() –Я–Њ—Б–ї–µ —Н—В–Њ–≥–Њ
—Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –ї–µ–Љ–Љ—Л –Њ—З–µ–≤–Є–і–љ–Њ, –≤–µ–і—М –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –Љ–∞—В—А–Є—Ж—Л A –љ–∞ –Љ–∞—В—А–Є—Ж—Л Xi(n), —Г
–Ї–Њ—В–Њ—А—Л—Е –њ—А–Є—А–∞–≤–љ–µ–љ—Л –љ—Г–ї—О –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –ї–µ–≤–Њ–≥–Њ –≤–µ—А—Е–љ–µ–≥–Њ "—Г–≥–ї–∞" (–Є–ї–Є
"–Њ–Ї–∞–є–Љ–ї–µ–љ–Є—П" –≤ —Б–ї—Г—З–∞–µ C), –і–∞–µ—В —В–Њ—В –ґ–µ —А–µ–Ј—Г–ї—М—В–∞—В, —З—В–Њ –Є –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ
–µ–і–Є–љ–Є—З–љ–Њ–є –Љ–∞—В—А–Є—Ж—Л.
–Я–Њ—Б–ї–µ —Н—В–Њ–≥–Њ
—Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –ї–µ–Љ–Љ—Л –Њ—З–µ–≤–Є–і–љ–Њ, –≤–µ–і—М –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –Љ–∞—В—А–Є—Ж—Л A –љ–∞ –Љ–∞—В—А–Є—Ж—Л Xi(n), —Г
–Ї–Њ—В–Њ—А—Л—Е –њ—А–Є—А–∞–≤–љ–µ–љ—Л –љ—Г–ї—О –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –ї–µ–≤–Њ–≥–Њ –≤–µ—А—Е–љ–µ–≥–Њ "—Г–≥–ї–∞" (–Є–ї–Є
"–Њ–Ї–∞–є–Љ–ї–µ–љ–Є—П" –≤ —Б–ї—Г—З–∞–µ C), –і–∞–µ—В —В–Њ—В –ґ–µ —А–µ–Ј—Г–ї—М—В–∞—В, —З—В–Њ –Є –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ
–µ–і–Є–љ–Є—З–љ–Њ–є –Љ–∞—В—А–Є—Ж—Л.
–Т
—Б–Є–ї—Г —Б–і–µ–ї–∞–љ–љ–Њ–≥–Њ –≤—Л—И–µ –Ј–∞–Љ–µ—З–∞–љ–Є—П –Њ –њ–Њ—А–Њ–ґ–і–∞—О—Й–Є—Е In,m —Б–њ–µ—Ж–Є–∞–ї–Є–Ј–∞—Ж–Є—П ![]() –Њ—В–Њ–±—А–∞–ґ–∞–µ—В
In,m+1 –≤ In,m. –Ю—В—Б—О–і–∞ —Г–ґ–µ –ї–µ–≥–Ї–Њ –њ–Њ–ї—Г—З–∞–µ—В—Б—П –Њ—Б–љ–Њ–≤–љ–∞—П —В–µ–Њ—А–µ–Љ–∞.
–Њ—В–Њ–±—А–∞–ґ–∞–µ—В
In,m+1 –≤ In,m. –Ю—В—Б—О–і–∞ —Г–ґ–µ –ї–µ–≥–Ї–Њ –њ–Њ–ї—Г—З–∞–µ—В—Б—П –Њ—Б–љ–Њ–≤–љ–∞—П —В–µ–Њ—А–µ–Љ–∞.
–Ґ–µ–Њ—А–µ–Љ–∞.
–Ъ–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ –∞–ї–≥–µ–±—А—Л K[M(n)m] –≤ K[M(n-1)m] (![]() –≤ —Б–ї—Г—З–∞–µ C)
–Є–љ–і—Г—Ж–Є—А—Г–µ—В —Н–њ–Є–Љ–Њ—А—Д–Є–Ј–Љ –Ї–Њ–ї–µ—Ж –Є–љ–≤–∞—А–Є–∞–љ—В–Њ–≤.
–≤ —Б–ї—Г—З–∞–µ C)
–Є–љ–і—Г—Ж–Є—А—Г–µ—В —Н–њ–Є–Љ–Њ—А—Д–Є–Ј–Љ –Ї–Њ–ї–µ—Ж –Є–љ–≤–∞—А–Є–∞–љ—В–Њ–≤.
–°–њ–Є—Б–Њ–Ї –ї–Є—В–µ—А–∞—В—Г—А—Л
Akin K., Buchsbaum D.A., Weyman J. Shur functors and Shur complexes// Adv. in Math. Vol.44. P.207-278 (1982).
–С–Њ—А–µ–ї—М –Р. –Ы–Є–љ–µ–є–љ—Л–µ –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Є–µ –≥—А—Г–њ–њ—Л. M.: –Ь–Є—А., 1972.
De Concini C., Procesi C. A characteristic free approach to invariant theory// Adv. in Math. 1976. Vol.21. P. 330-354.
Donkin S. The normality of conjugacy classes of matrices// Inv. Math., Vol.101. P.717-736 (1990).
Donkin S. Invariants of several matrices// Invent. Math. Vol.110. P.389-401 (1993).
Grotendick A., Dieudonne J. Elements de geometrie algebriques// Inst. Hautes Etudes Sci.Publ.Math. 4. 1960-1967.
Grosshans F. Observable subgroups and Hilbert's fourteenth problem// Am.J. Math. 95. P.229-253 (1973).
Humphreys J.E. Linear algebraic groups/ Springer Verlag. 1975.
Zubkov A.N. Endomorphisms of tensor products of exterior powers and Procesi hypothesis// Commun. in Algebra. 22(15). 6385-6399 (1994).