Реферат: Экспериментальные исследования электростатических полей с помощью электролитической ванны
Нижегородский Государственный Технический Университет.
Лабораторная работа по физике №2-24.
Экспериментальные исследования электростатических полей с помощью электролитической ванны
Выполнил студент
Группы 99 – ЭТУ
Наумов Антон Николаевич
Проверил:
Н. Новгород 2000г.
Цель работы: изучение метода моделирования электростатических полей в электролитической ванне и исследование их характеристик в пространстве между электродами различной формы.
Теоретическая часть.
Электростатическое поле - поле, создаваемое покоящимися электрическими зарядами.
Характеристиками этого поля являются напряженность
![]() и потенциал j, которые связаны между собой следующим соотношением:
и потенциал j, которые связаны между собой следующим соотношением: ![]() .
.
В декартовой системе координат: ![]() , где
, где ![]() единичные орты.
единичные орты.
Удобной моделью электрического поля является его изображение в виде силовых и эквипотенциальных линий.
Силовая линия - линия, в любой точке которой направление
касательной совпадает с направлением вектора напряженности ![]()
Эквипотенциальная поверхность - поверхность равного потенциала.
На практике электростатические поля в свободном пространстве создаются заданием на проводниках - электродах электрических потенциалов.
Потенциал в пространстве между проводниками
удовлетворяет уравнению Лапласа:![]() .
.
В декартовой системе координат оператор Лапласа: 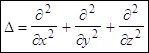 .
.
Решение уравнения Лапласа с граничными условиями на
проводниках![]() единственно и дает полную
информацию о структуре поля.
единственно и дает полную
информацию о структуре поля.
Экспериментальная часть.
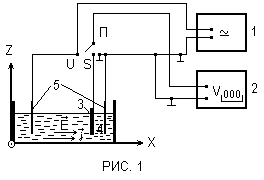
Схема экспериментальной установки.
|
Методика эксперимента:
|
В эксперименте используются следующие приборы: генератор сигналов Г3 (I), вольтметр универсальный B7 (2) c зондом (3), электролитическая ванна (4) с набором электродов различной формы (5).
Устанавливаем в ванну с дистилированной водой электроды. Собираем схему, изображенную на РИС. 1. Ставим переключатель П в положение “U”. Подготавливаем к работе и включаем приборы. Подаем с генератора сигнал частоты f=5 кГц и напряжением U=5 В, затем ставим переключатель П в положение “S”. Далее, помещаем в ванну электроды различной формы ( в зависимости от задания ) и затем, водя по ванне зондом, определяем 4 - эквипотенциальные линии: 1B, 2B, 3B, 4B. И так далее для каждого задания.
Задание №1. Исследование электростатического поля плоского конденсатора.
Таблица 1. Зависимость потенциала j от расстояния.
|
j = j (x),В |
x |
y |
j = j (x),В |
x |
y |
j = j (x),В |
x |
y |
j = j (x),В |
x |
y |
| 0 | -11 | 0 | 1,38 | -5 | 0 | 2,88 | 1 | 0 | 4,34 | 7 | 0 |
| 0,14 | -10 | 0 | 1,62 | -4 | 0 | 3,13 | 2 | 0 | 4,57 | 8 | 0 |
| 0,37 | -9 | 0 | 1,88 | -3 | 0 | 3,40 | 3 | 0 | 4,8 | 9 | 0 |
| 0,62 | -8 | 0 | 2,14 | -2 | 0 | 3,65 | 4 | 0 | 4,99 | 10 | 0 |
| 0,82 | -7 | 0 | 2,37 | -1 | 0 | 3,88 | 5 | 0 | 4,99 | 11 | 0 |
| 0,1 | -6 | 0 | 2,64 | 0 | 0 | 4,10 | 6 | 0 |
Таблица 2. Эквипотенциальные линии.
|
j = j (x),В |
x |
y |
j = j (x),В |
x |
y |
j = j (x),В |
x |
y |
j = j (x),В |
x |
y |
| 1 | -5,7 | 9 | 2 | -1,6 | 9 | 3 | 2,6 | 9 | 4 | 6,6 | 9 |
| 1 | -5,8 | 6 | 2 | -1,5 | 6 | 3 | 2,5 | 6 | 4 | 6,4 | 6 |
| 1 | -5,7 | 3 | 2 | -1,5 | 2 | 3 | 2,5 | 3 | 4 | 6,5 | 3 |
| 1 | -5,7 | 0 | 2 | -1,5 | 0 | 3 | 2,5 | 0 | 4 | 6,5 | 0 |
| 1 | -5,7 | -3 | 2 | -1,5 | -3 | 3 | 2,6 | -3 | 4 | 6,5 | -3 |
| 1 | -5,7 | -6 | 2 | -1,5 | -6 | 3 | 2,6 | -6 | 4 | 6,5 | -6 |
| 1 | -5,8 | -9 | 2 | -1,5 | -9 | 3 | 2,6 | -9 | 4 | 6,5 | -9 |
Обработка результатов измерений.
1). График зависимости ![]() .
.
2). Зависимость ![]() .
.
при x<0
![]()
при ![]()
![]()
при x>x2 ![]()
3). Погрешность измерения Е:
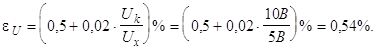
![]()
![]() .
.
![]()
![]()
Е = (Е ± dЕ) = (25 ± 0,15)![]()
4). Силовые и эквипотенциальные линии электростатического поля плоского конденсатора
5). Задача №1.
![]()
![]()
![]()
![]()
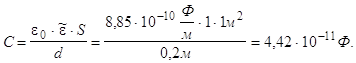
![]()
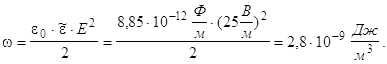
![]()
6). Задача №2.
![]() ;
; ![]()
![]()
Задание №2. Исследование электростатического поля цилиндрического конденсатора.
Радиусы цилиндров A =3,5 см, В=8,8см
Таблица
3. Зависимость ![]()
|
j=j(r),В |
r,см |
j=j(r),В |
r,см |
| 0,06 | 0 | 2,84 | 6 |
| 0,05 | 1 | 3,65 | 7 |
| 0,05 | 2 | 4,32 | 8 |
| 0,05 | 3 | 4,85 | 9 |
| 0,82 | 4 | 4,86 | 10 |
| 1,96 | 5 |
Таблица 4. Эквипотенциальные линии.
|
j=j(x,y) |
x |
y |
j=j(x,y) |
x |
y |
j=j(x,y) |
x |
y |
j=j(x,y) |
x |
y |
| 1 | 4 | 0 | 2 | 4,9 | 0 | 3 | 6,2 | 0 | 4 | 7,4 | 0 |
| 1 | 3,5 | 2 | 2 | 4,6 | 2 | 3 | 5,5 | 3 | 4 | 6,9 | 3 |
| 1 | 2,6 | 3 | 2 | 3 | 4 | 3 | 3,6 | 5 | 4 | 4,5 | 6 |
| 1 | 0 | 3,9 | 2 | 0 | 5 | 3 | 0 | 6,2 | 4 | 0 | 7,6 |
| 1 | -2,6 | 3 | 2 | -3,1 | 4 | 3 | -3,7 | 5 | 4 | -7 | 3 |
| 1 | -3,6 | 2 | 2 | -4,7 | 2 | 3 | -5,5 | 3 | 4 | -4,7 | 6 |
| 1 | -4,2 | 0 | 2 | -5,1 | 0 | 3 | -6,3 | 0 | 4 | -7,6 | 0 |
| 1 | -3,7 | -2 | 2 | -4,8 | -2 | 3 | -5,3 | -3 | 4 | -6,8 | -3 |
| 1 | -2,9 | -3 | 2 | -3,2 | -4 | 3 | -3,6 | -5 | 4 | -4 | -6 |
| 1 | 0 | -4 | 2 | 0 | -5,1 | 3 | 0 | -6,2 | 4 | 0 | -7,5 |
| 1 | 2,8 | -3 | 2 | -3 | -4 | 3 | 3,6 | -5 | 4 | 4,1 | -6 |
| 1 | 3,6 | -2 | 2 | -4,7 | -2 | 3 | 5,5 | -3 | 4 | 7 | -3 |
1). График зависимости j=j(r)
2). График зависимости j=j(ln r)
3). График зависимости E = E (r).
4). График зависимости E = E (1/r).
5). Эквипотенциальные линии.
6). Расчет линейной плотности t на электроде.
![]()
7). Задача №1.
L = 1м
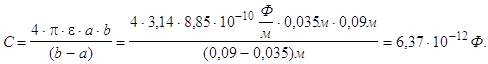
![]()
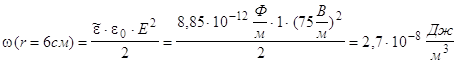
8). Задача №2.
r1 = 5см, r2 = 8см, l = 0,1м
![]()
![]()
Задание №3. Исследование электростатического поля вокруг проводников.
Таблица №5.
|
j=j(x,y) |
x |
y |
j=j(x,y) |
x |
y |
j=j(x,y) |
x |
y |
j=j(x,y) |
x |
y |
| 1 | -3,6 | 8 | 2 | 0,8 | 8 | 3 | 5,9 | 9 | 4 | 7,2 | 3 |
| 1 | -3,7 | 7 | 2 | 0,7 | 7 | 3 | 5,7 | 8 | 4 | 5,9 | 2 |
| 1 | -3,7 | 6 | 2 | 0,5 | 6 | 3 | 5,2 | 7 | 4 | 5,4 | 1 |
| 1 | -4 | 5 | 2 | 0,3 | 5 | 3 | 4,7 | 6 | 4 | 5,2 | 0 |
| 1 | -4,7 | 4 | 2 | 0,2 | 4 | 3 | 4,4 | 5 | 4 | 5,4 | -1 |
| 1 | -5 | 3 | 2 | 0,1 | 3 | 3 | 4,1 | 4 | 4 | 6,2 | -2 |
| 1 | -5,2 | 2 | 2 | 0,6 | -3 | 3 | 3,9 | 3 | 4 | 7,6 | -3 |
| 1 | -5,2 | 1 | 2 | 0,7 | -4 | 3 | 3,8 | 2 | |||
| 1 | -5 | 0 | 2 | 1 | -5 | 3 | 4,1 | -2 | |||
| 1 | -4,9 | -1 | 2 | 1,2 | -6 | 3 | 4,4 | -3 | |||
| 1 | -4,7 | -2 | 2 | 1,4 | -7 | 3 | 4,8 | -4 | |||
| 1 | -4,4 | -3 | 2 | 1,5 | -8 | 3 | 5,5 | -5 | |||
| 1 | -4,2 | -4 | 2 | 1,6 | -9 | 3 | 6 | -6 | |||
| 1 | -4 | -5 | 3 | 6,7 | -7 | ||||||
| 1 | -3,7 | -6 | 3 | 7,3 | -8 | ||||||
| 1 | -3,6 | -7 | 3 | 7,7 | -9 |
1). Потенциал на электродах: пластинке и втулке постоянен, то есть они являются эквипотенциальными поверхностями. Внутри полости потенциал также постоянен.
Таблица 6.
|
j=j(x,y) |
x |
y |
| 1,97 | -3 | 0 |
| 1,95 | 3 | 0 |
| 1,96 | 2 | -1 |
| 1,95 | -3 | -2 |
| 1,95 | 0 | 0 |
| 1,96 | -1 | 0 |
2). Распределение потенциала вдоль линии, охватывающей пластинку и расположенной на расстоянии
L = 3 мм от её края.
Таблица 7.
|
j=j(x,y) |
x |
y |
| 3,05 | 4 | 0 |
| 1,2 | -4,2 | 0 |
| 1,92 | 0 | -2,5 |
| 1,99 | 0 | 2 |
| 1,5 | -3 | 2,1 |
| 1,31 | -3 | -3 |
| 2,23 | 2 | -2 |
| 2,3 | 2 | 15 |
3). Эквипотенциальные линии.
4). Определение средней напряженности поля в нескольких точках вдоль силовой линии.
![]() .
.
а). 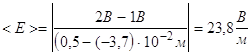
б). 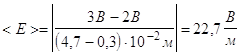
в). 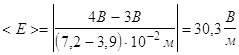
5).
![]() ,
, ![]() .
.
Таблица 8.
|
X, см |
y, см |
s, Кл/м2 |
E, В/м |
w, Дж/м3 |
| 4 | 0 |
3,24×10-9 |
366,6 |
5,95×10-7 |
| -4,2 | 0 |
2,21×10-9 |
250 |
2,77×10-7 |
| 0 | -5 |
8,85×10-11 |
10 |
4,43×10-10 |
| 0 | 2 |
1,18×10-10 |
13,3 |
7,82×10-10 |
| -3 | 2,7 |
1,33×10-9 |
150 |
9,96×10-8 |
| -3 | -3 |
1,9×10-9 |
213 |
2,00×10-7 |
| 2 | -2 |
8,23×10-10 |
93 |
3,80×10-8 |
| 2 | 1,5 |
1,02×10-9 |
116 |
5,95×10-8 |
Вывод. В ходе работы получены картины силовых и эквипотенциальных линий плоском и цилиндрическом конденсаторах, а также вокруг проводника, помещенного в электростатическое поле. Установлено, что проводники и полости внутри них в электростатическом поле являются эквипотенциальными поверхностями.
В плоском конденсаторе поле сосредоточено между пластинами, оно является однородным, а потенциал изменяется линейно.
В цилиндрическом конденсаторе поле также сосредоточено между пластинами, его напряженность обратно пропорциональна расстоянию от оси конденсатора до точки измерения. Потенциал изменяется логарифмически.
Поток вектора напряженности поля через коаксиальные с электродами цилиндрические поверхности постоянен, что совпадает с теоретическими предположениями (теорема Гаусса).