Реферат: Теорема вириала в преподавании физики и астрономии
А. И. Иванов, Л. П. Казанцева
Работа выполнена в предвидении изменения срока и содержания обучения в средней школе. В работе предлагается включить в программу обучения теорему вириала, что будет способствовать усилению связи в преподавании физики и астрономии, генерализации естественнонаучных знаний на основе общих закономерностей. Авторы приглашают к обсуждению целесообразности и возможности включения излагаемого фрагмента в содержание обучения физике и астрономии.
1. Теорема вириала утверждает, что для системы взаимодействующих частиц, находящихся в состоянии динамического равновесия, в том случае, когда все силы, действующие на частицы, являются внутренними по отношению к системе и обратно пропорциональны квадрату расстояния, средняя кинетическая энергия частиц равна половине среднего значения потенциальной энергии системы взаимодействующих тел, взятой с обратным знаком [1], т.е. выполняется равенство
![]() . . . . . . .
. . . (1)
. . . . . . .
. . . (1)
Потенциальная энергия взаимодействия тел в гравитационном поле также, как энергия взаимодействия электрических зарядов, является отрицательной [2], в отличие от кинетической, которая является всегда величиной положительной.
Строгое доказательство теоремы вириала достаточно сложно и связано с анализом дифференциальных уравнений, поэтому в условиях средней школы приходится иллюстрировать её на простых примерах.
Пусть
искусственный спутник массой m движется со скоростью ![]() по замкнутой
траектории на среднем расстоянии
по замкнутой
траектории на среднем расстоянии ![]() от центра
Земли, имеющей массу
от центра
Земли, имеющей массу ![]() . Кинетическая
энергия спутника равна
. Кинетическая
энергия спутника равна
![]() =
=![]() ,
,
а его потенциальная энергия
![]() = -
= - ![]() ,
,
где
![]()
![]()
![]()
![]()
![]() -
гравитационная постоянная.
-
гравитационная постоянная.
При движении спутника в гравитационном поле Земли на него действует центростремительная сила
![]() =
=![]()
Центростремительной силой, удерживающей спутник около Земли, является сила тяготения, обусловленная гравитационным взаимодействием между Землёй и спутником. По абсолютной величине она равна:
![]() =
=![]()
Следовательно, имеет место равенство
![]() =
=![]() . . . . . . .
. . . . .(2)
. . . . . . .
. . . . .(2)
Умножив
обе части этого равенства на ![]() , получим
, получим
![]() =
=![]() . . . . . . .
. . . . (3)
. . . . . . .
. . . . (3)
Таким образом, для энергетического состояния системы "Земля - спутник" справедлива теорема вириала.
В работе [3] применена теорема вириала при исследовании энергетического состояния лёгких атомов и их ионов. Результаты вычисления при этом хорошо согласуются с экспериментальными данными.
2. "Висячий" спутник Земли.
Для осуществления устойчивой межконтинентальной радио- и телевизионной связи в настоящее время широко используется искусственный спутник Земли.
Поставим
себе задачу: на какую высоту ![]() следует
"забросить" над экватором искусственный спутник Земли, чтобы он
неподвижно висел для наблюдателя, находящегося на Земле? Конечно, в этом случае
спутник и точка его запуска на экваторе должны двигаться в пространстве с
одинаковой угловой скоростью.
следует
"забросить" над экватором искусственный спутник Земли, чтобы он
неподвижно висел для наблюдателя, находящегося на Земле? Конечно, в этом случае
спутник и точка его запуска на экваторе должны двигаться в пространстве с
одинаковой угловой скоростью.
Теорема вириала в этом случае будет иметь вид
![]() =
=![]() ,
,
где: m - масса спутника,
![]() - масса Земли,
равная
- масса Земли,
равная ![]()
![]() -
гравитационная постоянная
-
гравитационная постоянная ![]()
![]() - расстояние
от центра Земли до спутника,
- расстояние
от центра Земли до спутника,
![]() - экваториальный
радиус Земли, равный 6378 км.
- экваториальный
радиус Земли, равный 6378 км.
Из теоремы вириала следует
![]() v
v![]()
При
этом v![]() - квадрат
линейной скорости спутника.
- квадрат
линейной скорости спутника.
Следовательно,
![]()
Подставив в полученную формулу числовые значения величин, получим
![]()
Расстояние
![]() от поверхности
Земли до спутника оказывается равным
от поверхности
Земли до спутника оказывается равным
![]()
![]()
На такую высоту надо поднять искусственный спутник над экватором. Это расстояние велико, но много меньше расстояния от Земли до Луны. Поэтому силой гравитационного взаимодействия между спутником и Луной можно пренебречь по сравнению с силой взаимодействия между спутником и Землёй. Следовательно, система Земля и её искусственный спутник представляет собой замкнутую систему и применение к ней теоремы вириала допустимо.
Представляет не меньший интерес определение положения искусственного спутника над любой точкой поверхности Земного шара. Подобные задачи можно предложить учащимся для самостоятельного решения и сравнения с действительными данными, что будет содействовать развитию творческих способностей обучаемых.
3.
Применение теоремы вириала к анализу энергетического состояния звёзд. В
современном понимании учёных-физиков звезда представляет собой громадный
газовый шар. Под действием гравитационных сил взаимодействия газ уплотняется,
температура его при этом увеличивается, и вследствие этого роста увеличивается
кинетическая энергия частиц. Электроны атома отрываются от поля ядра,
образуются свободные электроны и ионы водорода [4]. Некоторая часть протонов
объединяется по четыре, образуя ионы гелия. Молекулярная масса иона водорода
равна 0,5 атомных единиц, а для иона гелия она равна 2. С.А. Каплан считает [5]
обоснованным предположение, что в звёздных образованиях в средней ступени
эволюции, в которой находится в настоящее время наше Солнце, среднее значение
молекулярной массы частиц равно 0,6 или, что то же самое, ![]() атомных
единиц. Следовательно, среднее значение потенциальной энергии так называемой
водородной или "холодной" звезды оказывается равным
атомных
единиц. Следовательно, среднее значение потенциальной энергии так называемой
водородной или "холодной" звезды оказывается равным
![]()
![]()
![]() . . . . . . .
. . . . . (4)
. . . . . . .
. . . . . (4)
Из курса физики учащимся известно, что кинетическая энергия частицы газового шара равна
![]() =
=![]() , . . . . . .
. . . . . . (5)
, . . . . . .
. . . . . . (5)
где
![]()
![]()
![]() - постоянная
Больцмана.
- постоянная
Больцмана.
Число
всех частиц звёздного вещества (электронов и ионов) обозначим символом ![]() . Тогда,
считая плотность звёздного вещества одинаковой по всему объёму, кинетическую
энергию частиц звёздного образования выразим следующим образом:
. Тогда,
считая плотность звёздного вещества одинаковой по всему объёму, кинетическую
энергию частиц звёздного образования выразим следующим образом:
![]() =
=![]() =
=![]() . . . . . . .
. . . .(6)
. . . . . . .
. . . .(6)
Подставив известные значения потенциальной и кинетической энергий в формулу теоремы вириала, получим зависимость между радиусом и температурой звезды
![]()
![]()
Отсюда легко видеть, что при неизменной массе уменьшение радиуса звезды сопровождается соответствующим увеличением её температуры.
Для
удобства пользования полученной формулой в дальнейшем введём среднее расстояние
![]() между
соседними частицами из условия, что каждая пара частиц (протон и электрон)
находится внутри сферы диаметра
между
соседними частицами из условия, что каждая пара частиц (протон и электрон)
находится внутри сферы диаметра ![]() . Тогда объём
звезды определяется формулой
. Тогда объём
звезды определяется формулой
![]()
![]() ,
,
отсюда радиус звезды оказывается равным
![]()
![]()
![]() .
.![]()
Положив далее для массы звезды
![]() m
m![]()
![]() m
m![]()
![]() m
m![]()
(поскольку
масса протона m![]() много больше
массы электрона m
много больше
массы электрона m![]() ), теорему
вириала можно привести к виду
), теорему
вириала можно привести к виду
![]() =
=![]()
или
![]() =
=![]()
Эволюция
"холодной" звезды. Полученный результат полезно использовать для
описания пути звёздной эволюции. Вначале, когда звезда только формируется из
конденсирующего водородного облака, расстояние между частицами ![]() очень велико,
а температура
очень велико,
а температура ![]() - очень низка.
По мере того, как это облако под действием сил гравитационного притяжения
частиц сжимается,
- очень низка.
По мере того, как это облако под действием сил гравитационного притяжения
частиц сжимается, ![]() уменьшается, а
температура
уменьшается, а
температура ![]() возрастает.
При этом энергия частиц увеличивается, вследствие чего звезда начинает сильно
излучать.
возрастает.
При этом энергия частиц увеличивается, вследствие чего звезда начинает сильно
излучать.
Следует
при этом обратить внимание на то, что уменьшение расстояния ![]() между
взаимодействующими частицами сопровождается уменьшением их потенциальной
энергии гравитационного взаимодействия (от нуля в сторону отрицательных
значений). Следовательно, здесь имеет место переход потенциальной энергии
гравитационного притяжения в кинетическую энергию частиц и частично в энергию
излучения.
между
взаимодействующими частицами сопровождается уменьшением их потенциальной
энергии гравитационного взаимодействия (от нуля в сторону отрицательных
значений). Следовательно, здесь имеет место переход потенциальной энергии
гравитационного притяжения в кинетическую энергию частиц и частично в энергию
излучения.
Итак, путём элементарных рассуждений мы проследили эволюцию "холодной" звезды. Но ясно, что такой процесс не может продолжаться до бесконечности. Предел этому процессу ставит предел сжимаемости вещества, в свою очередь объяснимый конечностью размеров протона и электрона. Минимальное возможное расстояние между частицами звёздного вещества имеет порядок радиуса протона.
Мысль о том, что протон, электрон и нейтрон суть твёрдые непроницаемые шарики, конечно, ошибочная. Но в рамках современной теории и эксперимента, которые использует квантовая механика, электрон, протон и нейтрон в самом деле ведут себя так, словно обладают некоторым радиусом. Однако этот радиус зависит от импульса частицы и, следовательно, от её кинетической энергии. Чем выше импульс, тем меньше тот радиус, за которым частица становится как бы непроницаемой. Применяя эти соображения к протонам и электронам, можно принять минимальный диаметр элементарной сферы, внутри которой может находиться пара частиц (протон и электрон), равным учетверённому радиусу протона:
![]()
![]()
![]()
![]()
![]() .
.
Минимальная
масса звёзд. Звёзды излучают энергию в виде электромагнитных волн миллиарды
лет. Этот процесс поддерживается термоядерными реакциями, которые выделяют
энергию, достаточную для того, чтобы непрерывно пополнять (компенсировать) потерю
энергии вследствие излучения. Но чтобы внутри звезды могли идти термоядерные
реакции, необходимо, чтобы энергия реагирующих частиц составляла по порядку
величины не менее 0,1 Мэв, что соответствует средней температуре звезды порядка
![]()
![]() .
.
Имея
в виду это обстоятельство, можно легко подсчитать, какова должна быть
минимальная масса ![]() звезды, чтобы
в ней могли идти термоядерные реакции.
звезды, чтобы
в ней могли идти термоядерные реакции.
Из полученного выше соотношения
![]() =
=![]()
имеем
![]() =
=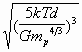
Подставим численные значения входящих в эту формулу величин
![]()
![]()
![]()
![]()
![]()
![]()
![]()
m![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
находим
![]()
![]()
![]() .
.
Эту величину полезно сопоставить с массой Солнца. Она равна
М☼![]()
![]()
![]() .
.
Следовательно,
самые маленькие звёзды должны иметь массы, равные приблизительно ![]() массы Солнца.
В звёздах, меньших по массе, термоядерные реакции не могут идти, и поэтому они
не могут длительное время излучать. Такие небесные объекты нельзя называть
звёздами.
массы Солнца.
В звёздах, меньших по массе, термоядерные реакции не могут идти, и поэтому они
не могут длительное время излучать. Такие небесные объекты нельзя называть
звёздами.
Максимальная
масса звезды. Звёзды, имеющие массу большую, чем масса Солнца, в процессе
эволюции сжимаются и становятся ещё более горячими. При достижении определённой
температуры (порядка ![]()
![]() ) в звёздном
образовании начинается термоядерная реакция, которая длительное время -
миллиарды лет - поддерживает излучающую способность звезды.
) в звёздном
образовании начинается термоядерная реакция, которая длительное время -
миллиарды лет - поддерживает излучающую способность звезды.
Для
горячих звёзд, где нельзя не учитывать энергию излучения, теорема вириала уже
не выполняется, поскольку излучение энергии приводит к тому, что звезда как
система частиц становится незамкнутой. Она через посредство поля излучения
взаимодействует с окружающей средой. Полная энергия ![]() звезды в этом
случае равна
звезды в этом
случае равна
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Если
энергия излучения звезды имеет порядок величины кинетической энергии звёздного
вещества (![]()
![]()
![]() ), то полная
энергия стремится к нулю, и достаточно незначительного увеличения энергии
излучения, чтобы звезда разлетелась на куски.
), то полная
энергия стремится к нулю, и достаточно незначительного увеличения энергии
излучения, чтобы звезда разлетелась на куски.
Следовательно, слишком горячие большие звёзды неустойчивы. Физическая причина этой неустойчивости состоит в том, что сила давления излучения и сила давления звёздного вещества внутри звезды превышает силу гравитационного сжатия звезды.
Максимальная масса звезды определяется из условия
![]()
![]()
![]()
Анализ
формулы ![]()
![]()
![]() мы не
приводим.
мы не
приводим.
Подробный расчёт показывает, что максимальная масса звёзд составляет 70 масс Солнца.
Большинство известных в настоящее время звёзд имеют массы приблизительно от 0,3 до 3,0 масс Солнца [6].
Таким образом, применение теоремы вириала в преподавании физики и астрономии позволяет проводить количественные исследования в самых интересных областях современной физики и астрофизики.
Список литературы
Слэтер Дж. Электронная структура молекул. М.: Мир, 1955. С.47-52, 77-80.
Фейнмановские лекции по физике. М.: Мир, 1967. Т. 1. С. 255.
Иванов А.И. Потенциалы ионизации легких атомов // Ярославский педагогический вестник. 2000. № 1. С.116-121.
Вайскопф В. Наука и удивительное. М.: Наука, 1965. С.189-196.
Каплан С.А. Физика звёзд. М.: Наука, 1965.
Физика космоса. Маленькая энциклопедия. М.: Советская энциклопедия, 1970. С.353.