Шпаргалка: Пример решения задачи по разделу «Переходные процессы»
Задача. Дана электрическая цепь, в которой происходит коммутация (Рис. 1). В цепи действует постоянная ЭДС Е. Требуется определить закон изменения во времени токов и напряжений после коммутации в ветвях схемы.
Задачу
следует решить двумя методами: классическим и операторным. На основании
полученного аналитического выражения построить график изменения искомой
величины в функции времени в интервале от t = 0 до t = ![]() , где
, где ![]() – меньший по
модулю корень характеристического уравнения.
– меньший по
модулю корень характеристического уравнения.
Параметры цепи: R1 = 15 Ом; R2 = 10 Ом; С = 10 мкФ; L = 10 мГ; Е = 100 В.
Решение.
Классический метод.
Решение задачи получается в виде суммы принужденного и свободного параметра:
i(t) = iпр(t) + iсв(t); u(t) = uпр(t)+ uсв(t), (1)
где
![]() , а
, а ![]() .
.
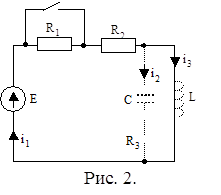 1. Находим токи и напряжения
докоммутационного режима для момента времени t = (0–). Так как сопротивление индуктивности постоянному току
равно нулю, а емкости – бесконечности, то расчетная схема будет выглядеть так,
как это изображено на рис. 2. Индуктивность закорочена, ветвь с емкостью
исключена. Так как в схеме только одна ветвь, то ток i1(0–)
равен току i3(0–), ток i2(0–) равен нулю, и в схеме всего один
контур.
1. Находим токи и напряжения
докоммутационного режима для момента времени t = (0–). Так как сопротивление индуктивности постоянному току
равно нулю, а емкости – бесконечности, то расчетная схема будет выглядеть так,
как это изображено на рис. 2. Индуктивность закорочена, ветвь с емкостью
исключена. Так как в схеме только одна ветвь, то ток i1(0–)
равен току i3(0–), ток i2(0–) равен нулю, и в схеме всего один
контур.
Составляем уравнение по второму закону Кирхгофа для этого контура:
![]() ,
,
откуда
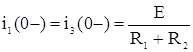 = 4 А.
= 4 А.
Напряжение на емкости равно нулю [uC(0–) = 0].
2. Определим токи и напряжения непосредственно после коммутации для момента времени t = 0+. Расчетная схема приведена на рис. 3. По первому закону коммутации iL(0–) = iL(0+), т.е. ток i3(0+) = 4 А. По второму закону коммутации uC(0–) = uC(0+) = 0.
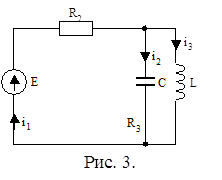 Для контура, образованного ЭДС Е,
сопротивлением R2 и емкостью С, согласно второго закона Кирхгофа имеем:
Для контура, образованного ЭДС Е,
сопротивлением R2 и емкостью С, согласно второго закона Кирхгофа имеем:
![]()
или
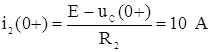 ;
;
i1(0+) = i2(0+) + i3(0+) = 14 А.
Напряжение на сопротивлении R2 равно Е – uC(0+) = 100 В, напряжение на индуктивности равно напряжению на емкости.
 3. Рассчитываем принужденные составляющие
токов и напряжений для
3. Рассчитываем принужденные составляющие
токов и напряжений для ![]() . Как и для докоммутационного режима
индуктивность закорачивается, ветвь с емкостью исключается. Схема приведена на
рис. 4. и аналогична схеме для расчета параметров докоммутационого режима.
. Как и для докоммутационного режима
индуктивность закорачивается, ветвь с емкостью исключается. Схема приведена на
рис. 4. и аналогична схеме для расчета параметров докоммутационого режима.
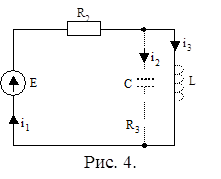
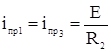 = 10 А;
= 10 А;
![]() = 100 В;
= 100 В; ![]() ;
; ![]()
4. Определяем свободные составляющие токов и напряжений для момента времени t = 0+, исходя из выражений i(0+) = iпр(0+) + iсв(0+) и u(0+) = uпр(0+) + uсв(0+).
iсв1(0+) = 4 А; iсв2(0+) =
10 А; iсв3(0+) = –6 А; uсвL(0+) = uсвС(0+) =
0; ![]() .
.
5. Определяем производные свободных токов и напряжений в момент времени непосредственно после коммутации (t = 0+), для чего составим систему уравнений, используя законы Кирхгофа для схемы, изображенной на рис. 3, положив Е = 0.
![]() ;
;
![]() (2)
(2)
![]()
Производную
тока через индуктивность можно найти, используя выражение: ![]() , а производную напряжения
на емкости – из уравнения
, а производную напряжения
на емкости – из уравнения ![]() . Т.е.
. Т.е.
![]() и
и ![]() ,
,
откуда
![]() ;
; ![]() (3)
(3)
Подставляя (3) в (2), после решения получаем:
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Все полученные результаты заносим в таблицу.
|
i1 |
i2 |
i3 |
uL |
uC |
uR2 |
|
| t = 0+ | 14 | 10 | 4 | 0 | 0 | 100 |
|
|
10 | 0 | 10 | 0 | 0 | 100 |
|
|
4 | 10 | –6 | 0 | 0 | 0 |
|
|
–105 |
–105 |
0 |
106 |
106 |
–106 |
6.
Составляем характеристическое уравнение. Для этого исключим в
послекоммутационной схеме источник ЭДС, разорвем любую ветвь и относительно
разрыва запишем входное сопротивление для синусоидального тока ![]() . Например, разорвем ветвь с сопротивлением R2:
. Например, разорвем ветвь с сопротивлением R2:
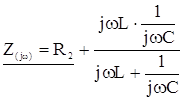 .
.
Заменим j на р и приравняем полученное уравнение нулю. Получим:
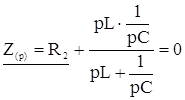
или
R2CLp2 + pL + R2 = 0.
Откуда находим корни р1 и р2.
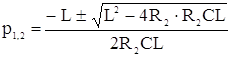 р1 = –1127,
р2 = –8873.
р1 = –1127,
р2 = –8873.
7. Определим постоянные интегрирования А1 и А2. Для чего составим систему уравнений:
![]() ;
;
![]()
или
![]() ;
;
![]()
Например, определим постоянные интегрирования для тока i1 и напряжения uL. Для тока i1 уравнения запишутся в следующем виде:
4 = А1i + А2i;
![]() .
.
После решения: А1i = –8,328 А, А2i = 12,328 А.
для напряжения uL:
![]() ;
;
![]() .
.
После
решения: ![]() = 129,1 В,
= 129,1 В, ![]() = –129,1 В.
= –129,1 В.
8. Ток i1 cогласно (1) изменяется во времени по закону:
i1(t) = 10 – 8,328е–1127t + 12,328e–8873t,
а напряжение uL:
uL(t) = 129,1e–1127t – 129,1 e–8873t.
| Электрические аппараты | |
|
Раздел 1. Основы теории электрических аппаратов Лекция № 1 Электрический аппарат - это электротехническое устройство, которое используется для ... При коротком замыкании величина тока в цепи не зависит от незначительных деформаций токоведущих контуров или от изменения расстояния между ними, возникающих под действием э. д. у ... Разъединители применяются для коммутации обесточенных с помощью выключателей участков токоведущих систем, для переключения присоединений распределительных устройств с одной ветви ... |
Раздел: Рефераты по физике Тип: учебное пособие |
| Энергосбережение на современном этапе | |
|
Введение Интерес к энергосбережению при освещении возобновился в условиях мирового экономического кризиса в 2008 г, заставившего обратить внимание на ... В уравнение, описывающее мгновенные значения сетевого напряжения uc необходимо ввести фазовый угол определяющий угол сдвига гармоник, представляющих напряжение на лампе ... Видно, что напряжение на балласте в момент перезажигания лампы зависит только от величины индуктивности балласта и характеристик лампы, и не зависит от Uc. |
Раздел: Рефераты по физике Тип: курсовая работа |
| Лекции по твердотельной электронике | |
|
Московский энергетический институт (технический университет) ТВЕРДОТЕЛЬНАЯ ЭЛЕКТРОНИКА Конспект лекций Москва, 2002 г. Содержание Лекция 1 5 1 ... Как видно из графика емкость pn перехода может изменяться в значительных пределах, что позволило использовать это свойство в управляемых напряжение полупроводниковых емкостях ... h12=u1/u2 - коэффициент обратной связи по напряжению, измеренный в режиме i1 = 0 - холостого хода по переменному току во входной цепи. |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| Проект электрокотельной ИГТУ | |
|
Содержание 1. Введение 1.1 Энергетика Иркутской области, перспективы развития 2. Общая часть 2.1 Краткая характеристика объекта и источников ... 3.7.2 Выбор схемы первичной коммутации на напряжение 220 кВ Важной характеристикой трансформатора тока является коэффициент трансформации К, равный отношению первичного тока I1 к вторичному I2 . |
Раздел: Рефераты по физике Тип: дипломная работа |
| Электричество и магнетизм | |
|
ОБЩИЙ ФИЗИЧЕСКИЙ ПРАКТИКУМ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ Ставрополь 2005 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ... Чтобы напряжение, подаваемое на вертикальный вход осциллографа, было пропорционально индукции магнитного поля В, между вторичной обмоткой и осциллографом ставят интегрирующую ... 5. Каков сдвиг фаз между током и напряжением, если в цепи есть только индуктивность или емкость; покажите это с помощью векторной диаграммы. |
Раздел: Рефераты по физике Тип: книга |