Дипломная работа: Ортогональные полиномы и кривые распределения вероятностей
Карпова Наталия Анатольевна
Санкт-Петербургский государственный университет
Санкт Петербург 2003
Введение.
Математическая статистика является наукой, которая изучает соотношения, столь глубоко проникающие в суть вещей, что их можно встретить при самых различных обстоятельствах. Результаты исследований, полученные с помощью аппарата математической статистики, используются в самых различных областях науки и техники, таких как биология, медицина, анатомия, геология, экология, экономика, и т.д.
Данная дипломная работа посвящена рассмотрению двух основных задач математической статистики:
получению кривой распределения вероятностей по имеющейся выборке;
нахождению зависимости между двумя случайными величинами, заданными своими выборками.
Для решения первой задачи используются различные методы. В данной работе рассмотрен метод Карла Пирсона, представителя английской школы статистики. Им было получено дифференциальное уравнение
![]() ,
,
а так же введен критерий æ (каппа Пирсона), с помощью которого Пирсон классифицировал решения этого дифференциального уравнения и представил их в виде двенадцати типов.
Позже в своих теоретических исследованиях Колмогоров А. Н. и Марков А. А. доказали, что любой закон распределения может быть записан в виде одного из двенадцати типов кривых Пирсона, поэтому для решения данной задачи используется метод Пирсона нахождения кривой распределения.
Для решения второй задачи используется метод П.Л. Чебышева, создателя Санкт – Петербургской математической школы. В статистике имя знаменитого русского математика П. Л. Чебышева (1821-1894) известно главным образом по так называемому неравенству Чебышева, которое он предложил для распределения вероятностей, и которое имеет силу для любого статистического распределения численностей.
Однако за последнее время в статистике всё большее значение приобретают ортогональные полиномы Чебышева, которые имеют особое значение при определении множественной и криволинейной регрессии и при вычислении коэффициентов обобщённой функции нормального распределения вероятностей.
Чебышев предложил общую интерполяционную формулу, при которой возможно интерполирование в самых разнообразных случаях. Эта интерполяционная формула удовлетворяет условиям метода наименьших квадратов и выражена при помощи его ортогональных полиномов. Общая интерполяционная формула, или, иначе ряд Чебышева, предложен Чебышевым в 1855 году. Она имеет вид
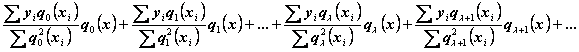 .
.
Таким образом в дипломной работе рассматриваются два метода:
метод Пирсона нахождения кривых распределения вероятностей,
метод Чебышева получения ортогональных полиномов,
которые были положены в основу обобщенного метода Грамма – Шарлье нахождения кривой распределения вероятностей.
Глава 1. Система кривых Пирсона.
В данной главе ставится задача нахождения закона распределения случайной величины в удобном для практического использования виде. Для ее решения рассматривается подход К. Пирсона, который является выдающимся представителем английской статистической школы.
§ 1. Дифференциальное уравнение Пирсона.
Рассмотрим
случайную величину, заданную своей выборкой ![]() , таким образом, можем записать
, таким образом, можем записать ![]() - статистической
распределение. Ставится задача нахождения закона распределения случайной
величины в удобном для практического использования виде.
- статистической
распределение. Ставится задача нахождения закона распределения случайной
величины в удобном для практического использования виде.
Метод Пирсона заключается в том, что мы рассматриваем дифференциальное уравнение Пирсона:
![]() (1)
(1)
и исследуем, какие решения можно получить при различных значениях параметров уравнения (1).
Общий интеграл этого уравнения представим в виде:
![]()
где
![]() .
.
Значение этого неопределенного интеграла зависит от корней уравнения
![]() (2),
(2),
следовательно, от его дискриминанта
![]()
который можно написать в виде
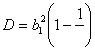 ,
,
вводя параметр
æ![]() .
.
Или иначе, величину æ можно представить в виде:
æ![]() ,
,
где
величины ![]() представимы через
центральные моменты статистических распределений
представимы через
центральные моменты статистических распределений ![]() к-го порядка, которые
определяются по формуле
к-го порядка, которые
определяются по формуле
![]() ,
,
где
![]() есть
есть
![]() .
.
Тогда
![]() ,
, ![]() .
.
Через
величины ![]() можно представить и
величины
можно представить и
величины ![]() следующим образом [5]:
следующим образом [5]:
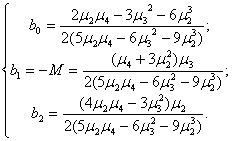
Величина æ называется критерием Пирсона (каппа Пирсона) и различные значения ее дают нам следующие выводы о корнях уравнения:
А.
Если æ![]() , то
, то ![]() и уравнение (1) имеет
вещественные корни различных знаков.
и уравнение (1) имеет
вещественные корни различных знаков.
В.
Если 0< æ<1, то ![]() и уравнение (1) имеет
комплексные корни.
и уравнение (1) имеет
комплексные корни.
С.
Если æ>1, то ![]() и уравнение (1) имеет
вещественные корни одного знака.
и уравнение (1) имеет
вещественные корни одного знака.
Соответственно
этим случаям Пирсон различает три главных типа своих кривых, которые он назвал
соответственно типами I, IV и VI. Затем æ может равняться ![]() , что дает переходные типы кривых. Наконец, присоединяя
некоторые дополнительные условия, мы можем увеличить число переходных типов.
Всего система кривых Пирсона заключает 12 типов и нормальную кривую.
, что дает переходные типы кривых. Наконец, присоединяя
некоторые дополнительные условия, мы можем увеличить число переходных типов.
Всего система кривых Пирсона заключает 12 типов и нормальную кривую.
В своих разработках Колмогоров А. Н. и Марков А. А. доказали, что любой закон распределения может быть записан в виде одного из двенадцати типов кривых Пирсона, поэтому для решения задачи идентификации используется метод Пирсона.
§ 2. Основные типы кривых Пирсона.
В этом параграфе будут рассмотрены основные типы кривых распределения вероятностей, предложенные и классифицированные Пирсоном.
Тип I.
Пусть æ<0. Тогда
![]()
и
уравнение (2) имеет вещественные корни различных знаков: ![]() , так что можем записать
, так что можем записать
![]() .
.
Тогда правая часть уравнения (1) может быть представлена в виде:
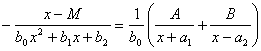 ,
,
где
![]() .
.
Пусть еще
![]() .
.
Тогда уравнение (1) перепишется в виде
![]()
и общий интеграл его можно представим в виде
![]() ,
,
где
![]() и значения
и значения ![]() и
и ![]() должны удовлетворять условиям
должны удовлетворять условиям
![]() .
.
Тип
I получается, если ![]() заключается в интервале
заключается в интервале ![]() . Тогда
. Тогда
![]() и
и ![]()
или, как обычно пишут
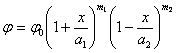 .
.
Так
как ![]() выражаются определенным образом через моменты
выражаются определенным образом через моменты ![]() , то,
очевидно, и
, то,
очевидно, и ![]() также выражаются через те же моменты. Для
этого введем число
также выражаются через те же моменты. Для
этого введем число
![]() .
.
Тогда простое преобразование дает следующие формулы:
 .
.
Эти формулы используются вообще при вычислении параметров и других кривых Пирсона.
Далее, пользуясь этими же формулами,
![]() ,
,
следовательно,
![]() .
.
Затем
![]() ,
,
или, после простых подсчетов,
![]() ,
,
где
![]() .
.
Таким
образом, ![]() и
и ![]() представляют корни уравнения
представляют корни уравнения
![]() ,
,
Когда
найдены ![]() и
и ![]() ,
, ![]() и
и ![]() находятся по формулам
находятся по формулам
![]() ,
,
в которых
![]() ,
, ![]() .
.
Здесь использовано равенство
![]() ,
,
которое получается, так мы имеем
![]() ,
,
и
![]() ,
,
следовательно,
![]() ,
,
откуда
![]()
(так
как ![]() ), нужно брать
), нужно брать
![]() .
.
Таким
образам, ![]() и
и ![]() есть корни уравнения
есть корни уравнения
![]()
и
![]() и
и ![]() по формулам
по формулам
![]() ,
,
в которых
![]() ,
,
где
![]() находится из равенства
находится из равенства
![]() .
.
Остается
найти ![]() . Оно
находится по равенству
. Оно
находится по равенству
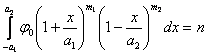 .
.
При помощи подстановки
![]()
мы находим:
 .
.
Следовательно,
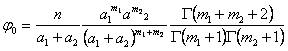 .
.
Тип IV.
Второй главный тип кривых Пирсона, соответствующий значениям
0< æ<1, когда уравнение (1) имеет комплексные корни.
Пусть эти корни равны
![]() ,
,
где
![]() .
.
Тогда уравнение (1) будет
![]() ,
,
откуда
![]() ,
,
и
![]() ,
,
или
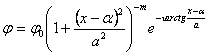 ,(3)
,(3)
причем
![]() .
.
Параметры
кривой (3), выражаются следующим образом через моменты ![]() и константы
и константы ![]() :
:
![]()
(здесь
![]() , и
, и ![]() ),
),
![]() ,
,
где
![]() - функция Пирсона, определяемая равенством
- функция Пирсона, определяемая равенством
 .
.
Интеграл в правой части можно привести к другому виду:
подстановка
![]()
приводит его к виду
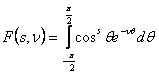 .
.
Обычно, полагая
![]() ,
,
пишут
![]() в виде
в виде
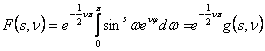 ,
,
где
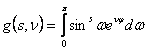 .
.
Тип VI.
Третий главный тип кривых Пирсона, соответствующий значениям критерия æ>1 . В этом случае уравнение (2) имеет вещественные корни одного знака. Не приводя вывода уравнения кривой типа VI, аналогичного выводу уравнения кривой типа I [5], прямо приведем уравнение, отнесенное к средней выравниваемого распределения, как началу координат:
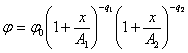
(в
нем ![]() ). Его
параметры вычисляются по формулам:
). Его
параметры вычисляются по формулам:
![]() ,
,
причем
берется ![]() , если
, если ![]() и
и ![]() , если
, если ![]() ;
; ![]() и
и ![]() дают выражения:
дают выражения:
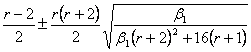 ,
,
причем
должно быть ![]() ;
;
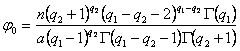 ,
,
и
![]() .
.
Уравнение кривой типа VI пишут также в виде:
![]()
беря за начало координат точку
![]() .
.
Параметры
![]() вычисляются как выше, а
вычисляются как выше, а ![]() имеет теперь такое выражение:
имеет теперь такое выражение:
![]() .
.
Кривая
простирается от ![]() до
до ![]() , если
, если ![]() , и от
, и от ![]() до
до ![]() , если
, если ![]() .
.
§ 3. Переходные типы кривых Пирсона.
Переходные
типы кривых Пирсона получаются при специальных значениях критерия æ и при
некоторых условиях, налагаемых на ![]() и
и ![]() .
.
Тип II.
Получается
при æ=0,![]() и имеет
уравнение
и имеет
уравнение
![]() ,
,
отнесенное к моде, которая теперь равна средней (кривая симметрична относительно начала). Ее параметры вычисляются по формулам
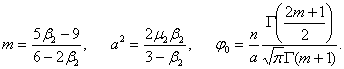
Кривая
простирается от -а до а. На концах распределения ![]() , если
, если ![]() и
и ![]() , если
, если ![]() . Эта кривая
имеет так называемую U-образную форму с антимодой вместо моды.
. Эта кривая
имеет так называемую U-образную форму с антимодой вместо моды.
Тип VII.
Имеет уравнение
![]() ,
,
получается
при æ=0,![]() и имеет
параметры
и имеет
параметры
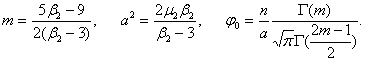
Нчало координат в средней (средняя равна моде).
Тип III.
Имеет уравнение
![]()
с началом координат в моде и с параметрами
![]()
![]() .
.
Получается
при æ![]()
Тип V.
Имеет уравнение
![]()
с параметрами
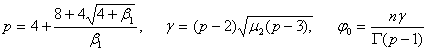
кривая получается при æ=1 и бесконечна в одном направлении.
Тип VIII.
Имеет уравнение
![]() ,
,
простирается от –а до 0, получается при
æ![]() ,
,
причем
![]() зависит от
зависит от ![]() , а параметр т
получается как решение уравнения
, а параметр т
получается как решение уравнения
![]()
и он не должен быть больше 1 или меньше 0.
Тогда
![]() ,
,
а начало в точке
![]()
Тип IX.
Имеет уравнение
![]() ,
,
простирается от –а до 0, получается при
æ![]()
Параметр т определяется как решение уравнения
![]()
Тогда
![]() ,
,
а начало будет в точке
![]()
Тип X.
Имеет уравнение
![]()
с
началом координат в точке ![]() ; получается
как специальный случай кривой типа III при
; получается
как специальный случай кривой типа III при ![]() .
.
Тип XI
Имеет уравнение
![]() ,
,
получается при
æ![]()
и
простирается от ![]() до
до ![]() , а т
находится из уравнения
, а т
находится из уравнения
![]()
и b зависит от m.
Тогда
![]() ,
,
а начало координат в точке
![]() .
.
Тип XII.
Имеет уравнение
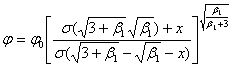 ,
,
получается при
æ![]() .
.
Кривая
простирается от ![]() до
до ![]() , начало
координат в точке
, начало
координат в точке ![]() и
и
![]() .
.
Тип N.
Тринадцатый тип кривых распределения Пирсона – нормальная кривая с уравнением
![]() ,
,
которая получается при условиях
æ![]() .
.
Типы II, VI, VII, VIII, IX представляют специальные случаи кривой типа I, тип X – специальный случай типа III, а тип XI - типа VI. [5] (См. приложение 1.)
Глава 2. Применение ортогональных полиномов Чебышева при нахождении кривых распределения вероятностей.
В этой главе рассмотрено получение ортогональных полиномов способом, который разработал П. Л. Чебышев. А именно, через разложение в непрерывную дробь суммы
![]()
и рассмотрение знаменателей подходящих дробей полученной непрерывной дроби. Причем показано, что полученные таким образом ортогональные полиномы отвечают условиям метода наименьших квадратов, а так же показано их применение для нахождения кривых распределения вероятностей.
§ 1. Получение ортогональных полиномов по способу Чебышева.
Пусть
даны значения интерполируемой функции![]()
![]()
![]() ,
,
соответствующие
значения аргумента ![]()
![]() . Каждому
значению аргумента
. Каждому
значению аргумента ![]() ставится в соответствие частота
ставится в соответствие частота ![]() .
.
Требуется найти такую целую функцию
![]() ,
,
где
![]() , которая
удовлетворяла бы условию наименьшего значения суммы
, которая
удовлетворяла бы условию наименьшего значения суммы
![]() .
.
В
данной задаче в качестве веса ![]() предлагается рассмотреть [8]
предлагается рассмотреть [8]
![]() ,
,
где n есть
![]()
или
иначе говоря n - сумма всех испытаний.
Для
решения нашей задачи находим коэффициенты ![]() , которые
определяются из следующих уравнений
, которые
определяются из следующих уравнений
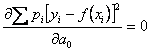 ;
;
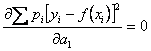 ;
;
……………………
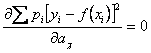 ;
;
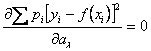 ;
;
После
преобразований получаем следующую систему уравнений для нахождения
коэффициентов ![]()
![]() ;
;
![]() ;
;
……………………
……………………
![]() ;
;
……………………
![]() ;
;
где
![]()
![]()
Такой подход к нахождению коэффициентов имеет существенный недостаток – при повышении степени полинома хотя бы на единицу приходится переписывать все уравнения и решать систему заново.
Есть другой вариант построения искомого полинома [8].
Пусть
будет ![]() целая функция от
целая функция от ![]() степени
степени ![]() , которая
обращается в
, которая
обращается в ![]() при
при ![]() . Положим
. Положим
![]() ,
,
где
![]() - целые функции степеней
- целые функции степеней ![]() , а
, а ![]() - коэффициенты.
- коэффициенты.
Пусть
теперь сумма ![]() первых членов выражения
первых членов выражения ![]()
![]()
равняется
![]() ,
,
т.е.
![]() .
.
Каковы
в этом случае условия относительно ![]() и
и ![]() при которых сумма
при которых сумма
![]()
имеет наименьшее значение?
Обозначим
эту сумму через ![]() :
:
![]() ,
,
и, подставляя в нее
![]() ,
,
составляем обычным способом дифференцирования следующие уравнения:
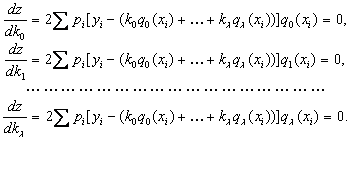
Отсюда следует:
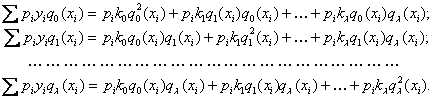
Так
как ![]() есть ортогональные полиномы по построению,
следовательно все слагаемые вида
есть ортогональные полиномы по построению,
следовательно все слагаемые вида ![]() будут равняться 0.
будут равняться 0.
В
результате преобразований получим выражения для коэффициентов ![]() :
:
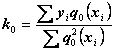 ;
;
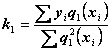 ;
;
………………
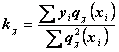 ;
;
………………
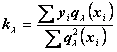 .
.
Теперь можно представить функцию
![]()
в таком виде
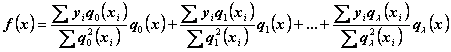 .
.
Легко
убедиться, что для перехода от найденного выражения интерполируемой функции к
целой функции степени ![]() , достаточно к
левой части полученной функции приписать один новый член
, достаточно к
левой части полученной функции приписать один новый член
 .
.
Для
дальнейшего перехода к целой функции степени ![]() , также
удовлетворяющей условию наименьшего значения суммы
, также
удовлетворяющей условию наименьшего значения суммы
![]() ,
,
достаточно
прибавить к найденному выражению функции степени ![]() , такой новый
член
, такой новый
член
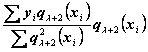 .
.
Таким образом, решение задачи параболического интерполирования по способу наименьших квадратов приводится к нахождению ряда
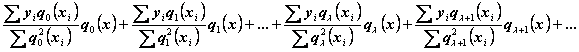
Этот
ряд, обладающий свойством давать посредством суммы своих ![]() первых членов
приближенное представление интерполируемой функции в виде целой функции степени
первых членов
приближенное представление интерполируемой функции в виде целой функции степени
![]() ,
удовлетворяющей требованию наименьших квадратов, называется интерполяционным
рядом Чебышева.
,
удовлетворяющей требованию наименьших квадратов, называется интерполяционным
рядом Чебышева.
Теперь
для полного решения задачи остается еще узнать, что представляют собой функции ![]() , определив
через данные величины
, определив
через данные величины ![]() и
и ![]() коэффициенты при
коэффициенты при ![]() в выражении этих функций.
в выражении этих функций.
Далее, с помощью разложения дроби
![]()
по
нисходящим степеням ![]() получим, что дробь
получим, что дробь
![]() ,
,
где
![]() ,
,
дает приближенное представление функции [7]
![]()
с точностью до членов степени
![]()
включительно.
Здесь ![]() есть весовая функция, найденная ранее по
методу Пирсона. Но эта дробь, у которой степень числителя на единицу меньше
степени знаменателя, при разложении в непрерывную дробь всегда будет в своих
неполных частных содержать переменную
есть весовая функция, найденная ранее по
методу Пирсона. Но эта дробь, у которой степень числителя на единицу меньше
степени знаменателя, при разложении в непрерывную дробь всегда будет в своих
неполных частных содержать переменную ![]() в первой степени. Следовательно, знаменатели
ее подходящих дробей
в первой степени. Следовательно, знаменатели
ее подходящих дробей ![]() есть функции
степеней
есть функции
степеней ![]() ; поэтому
можно положить
; поэтому
можно положить
![]() .
.
Что
касается ![]() , то его можно
приравнять
, то его можно
приравнять ![]() .
.
Разлагая
![]()
в непрерывную дробь вида
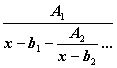 ,
,
где
![]() и
и ![]() - некоторые постоянные, используем найденные
выше свойства функции
- некоторые постоянные, используем найденные
выше свойства функции ![]() для определения этих постоянных через данные
значения
для определения этих постоянных через данные
значения ![]() .
.
Выражения
для ![]() будет иметь вид:
будет иметь вид:
![]() .
.
Выражения
для коэффициентов ![]() будут следующими:
будут следующими:
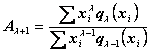 .
.
Вводя для сокращения обозначение
![]()
через
![]() , запишем
выражение для
, запишем
выражение для ![]() в таком виде:
в таком виде:
![]() .
.
Для
![]() выражение будет иметь вид
выражение будет иметь вид
![]() .
.
Что
касается величин ![]() и
и ![]() , то они равны
соответственно
, то они равны
соответственно
![]() и
и ![]() .
.
Теперь
перейдем к определению коэффициентов ![]() в выражении
в выражении
![]() .
.
Для
![]() получим
выражение
получим
выражение
![]() .
.
Это
выражение весьма упростится, если ![]() мы будем считать отклонениями данных значений
аргумента от его средней арифметической так, что
мы будем считать отклонениями данных значений
аргумента от его средней арифметической так, что ![]() . Тогда
. Тогда ![]() , а выражение
для
, а выражение
для ![]() будет иметь вид
будет иметь вид
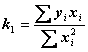 .
.
Также упростятся выражения для
![]() и
и 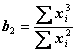 .
.
Функция
![]() станет равной
станет равной ![]() , функции
, функции ![]() определяются путем последовательных
подстановок выражений
определяются путем последовательных
подстановок выражений ![]() в формулы
в формулы
![]() .
.
При помощи этих формул можно вычислить какой угодно член ряда Чебышева
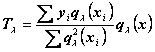 .
.
Оценка результатов интерполирования производится при помощи среднего квадратического отклонения данных значений интерполируемой функции от вычисленных по найденному уравнению параболы.
Обозначим
сумму квадратов отклонений через ![]() . Тогда можно
написать
. Тогда можно
написать
![]() .
.
![]() будет
равняться
будет
равняться
![]() ,
,
а
![]() выражать
рекуррентно через
выражать
рекуррентно через ![]() по формуле
по формуле
![]() .
.
Итак,
![]() ,
, ![]() ,
, ![]() ,
,
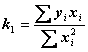 ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Мы
видим, что в зависимости от нашей весовой функции ![]() в разложении мы получим разные системы
ортогональных полиномов.
в разложении мы получим разные системы
ортогональных полиномов.
§ 2. Обобщение Грамма - Шарлье.
Пусть
по методу Пирсона найден вид кривой распределения вероятностей ![]() на соответствующем интервале. Теперь, для
представления в удобном для практического использования виде, запишем
полученную кривую в несколько иной форме. Для этого используем обобщение Грамма
– Шарлье, которое основывается на применении ортогональных полиномов Чебышева и
состоит в том, что кривая распределения вероятностей представима в виде
следующего разложения:
на соответствующем интервале. Теперь, для
представления в удобном для практического использования виде, запишем
полученную кривую в несколько иной форме. Для этого используем обобщение Грамма
– Шарлье, которое основывается на применении ортогональных полиномов Чебышева и
состоит в том, что кривая распределения вероятностей представима в виде
следующего разложения:
![]() (4)
(4)
где
![]() - есть к–ая производная функции
- есть к–ая производная функции ![]() . Здесь
полагаем, что
. Здесь
полагаем, что
![]() .
.
Таким
образом, мы получаем кривую распределения вероятностей теперь уже в виде ![]() .
.
Производные
функции ![]() мы можем представить в виде [3]
мы можем представить в виде [3]
![]() ,
,
тогда можем записать
![]()
где
функции ![]() должны удовлетворять следующему свойству:
должны удовлетворять следующему свойству:
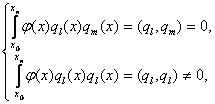 если
если ![]() (5)
(5)
А
коэффициенты ![]() получаются из равенства (4) с помощью
домножения на любой из ортогональных полиномов
получаются из равенства (4) с помощью
домножения на любой из ортогональных полиномов ![]() и, интегрирования полученного равенства:
и, интегрирования полученного равенства:
![]() =
=
![]()
=![]()
Отсюда следует, что
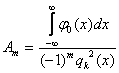 .
.
На практике в этом разложении мы используем только четыре первых члена, и коэффициенты перед ними есть:
![]()
![]()
![]()
Коэффициенты
![]() имеют четкий статистический смысл, а именно:
коэффициент
имеют четкий статистический смысл, а именно:
коэффициент ![]() , выраженный
через
, выраженный
через ![]() , отвечает за
асимметрию закона распределения, и коэффициент
, отвечает за
асимметрию закона распределения, и коэффициент ![]() выраженный через
выраженный через ![]() - за эксцесс или дефект кривой распределения.
- за эксцесс или дефект кривой распределения.
Свойство
(5) есть свойство ортогональности полиномов, т. е. ![]() по определению является системой ортогональных
полиномов, которая получена по способу Чебышева в предыдущем параграфе [3],
[5].
по определению является системой ортогональных
полиномов, которая получена по способу Чебышева в предыдущем параграфе [3],
[5].
§ 3. Весовые функции и системы ортогональных полиномов.
В общей теории ортогональных полиномов известно, что система ортогональных полиномов называется классической, если она ортогональна относительно весовой функции, которая является решением дифференциального уравнения Пирсона [2], [6]. То есть, здесь прослеживается связь между теорией классических ортогональных полиномов и задачами математической статистики (нахождением закона распределения вероятностей).
Полиномы Чебышева - Эрмита.
Пусть многочлен (2) не имеет корней, тогда уравнение Пирсона (1) после переноса начала координат запишется в виде
![]() ,
,
тогда решение этого уравнения запишется в виде
![]() (6).
(6).
Линейным преобразованием независимого переменного
![]()
эта
функция приводится с точностью до постоянного множителя ![]() к весовой функции многочленов Чебышева –
Эрмита, которая имеет вид
к весовой функции многочленов Чебышева –
Эрмита, которая имеет вид
![]() .
.
Поскольку
умножение весовой функции на постоянную практически не изменяет ортогональные
многочлены, то в формуле (6), как и в аналогичных нижеследующих формулах, не
нарушая общности, можно полагать ![]() . В данном
случае ортогональные многочлены с весом (6) выражаются через ортогональные
многочлены Чебышева – Эрмита
. В данном
случае ортогональные многочлены с весом (6) выражаются через ортогональные
многочлены Чебышева – Эрмита ![]() по формуле
по формуле
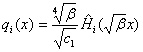 .
.
В этом случае условие ортогональности запишется в виде:
 если
если ![]()
Полиномы Чебышева - Лагерра.
Пусть теперь многочлен (2) имеет один корень. Тогда уравнение (1) представимо в виде
![]() .
.
Тогда его решение запишется в виде
![]() .
.
Многочлены, ортогональные с таким весом, можно рассматривать как обобщение многочленов Чебышева – Лагерра, ортогональных с весом
![]() .
.
Причем
и здесь можно выразить эти многочлены через многочлены Чебышева – Лагерра ![]() , а условие
ортогональности будет:
, а условие
ортогональности будет:
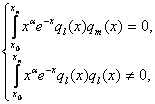 если
если ![]()
Полиномы Якоби.
Предположим,
что многочлен (2) имеет два различных действительных нуля. Тогда ![]() , и уравнение
Пирсона (1) представимо в виде
, и уравнение
Пирсона (1) представимо в виде
![]() ,
,
где
![]() и
и ![]() - некоторые постоянные и
- некоторые постоянные и ![]() . Тогда
решение уравнения (1)
. Тогда
решение уравнения (1)
представимо в виде
![]()
и
определяет некоторую систему ортогональных многочленов, которая линейным
преобразованием независимого переменного и умножением на постоянную сводится к
системе многочленов Якоби ![]() . Так как
весовая функция многочленов Якоби имеет вид
. Так как
весовая функция многочленов Якоби имеет вид
![]() .
.
И соответственно условие ортогональности будет иметь вид:
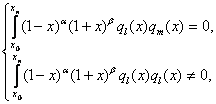 если
если ![]()
Многочлены Чебышева I рода являются частным случаем многочленов Якоби, так как весовая функция, относительно которой ортогональны эти многочлены, имеет вид:
![]()
и
получается при подстановке в весовую функцию многочленов Якоби параметров ![]() .
.
Многочлены Чебышева II рода так же являются частным случаем многочленов Якоби, так как весовая функция многочленов Чебышева II рода имеет вид
![]()
и
получается при подстановке в весовую функцию многочленов Якоби параметров ![]() .
.
Следует так же отметить, что многочлены Лежандра являются частным случаем многочленов Якоби, так как весовая функция многочленов Лежандра
![]()
и
есть частный случай весовой функции многочленов Якоби при ![]() .
.
Глава 3. Примеры нахождения кривых распределения вероятностей и программное обеспечение.
В этой главе рассматриваются примеры нахождения кривых распределения по методу кривых Пирсона с использованием теоретических исследований, рассмотренных в первой и второй главах дипломной работы. Было написано программное обеспечение, с помощью которого были получены и проинтерпретированы численные результаты.
§ 1. Примеры нахождения кривых распределения вероятностей.
Рассмотрение примеров заключалось в том, что было рассмотрено пятьдесят случайных выборок, а далее были рассмотрены примеры выборок с заданным законом распределения. Согласно рассмотренному ниже алгоритму были произведены соответствующие вычисления, и по каждой выборке была построена кривая распределения вероятностей. При проведении испытаний было получено, что кривая распределения сорока семи из пятидесяти рассмотренных выборок есть кривая Пирсона первого типа, которая определяется следующей формулой:
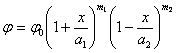 .
.
Здесь
нужно отметить разнообразие кривых Пирсона, делающее их применение очень
гибким. Это означает, что кривые распределения вероятностей первого типа при
различных значениях параметров ![]() и
и ![]() могут иметь различную форму.
могут иметь различную форму.
Ниже рассмотрено несколько примеров наиболее часто встретившихся форм кривой распределения I типа.
Пример 1.
Рассмотрим выборку:
|
|
|
|
|
| 1 | 10,55233622 | 2 | Кривая распределения вероятностей первого типа. |
| 2 | 13,44763172 | 2 | |
| 3 | 17,80800986 | 1 | |
| 4 | 4,963081479 | 2 | Параметры кривой: |
| 5 | 14,66424847 | 2 | |
| 6 | 12,436602 | 1 |
|
| 7 | 9,36697793 | 2 |
|
| 8 | 15,20854056 | 1 |
|
| 9 | 15,66078138 | 2 |
|
| 10 | 8,748272777 | 2 |
|
| 11 | 9,028156996 | 1 | |
| 12 | 18,93642914 | 2 | |
| 13 | 18,84283829 | 1 | |
| 14 | 14,6049341 | 1 |
Следовательно,
кривая распределения вероятностей будет определена на промежутке ![]()
![]() и будет иметь вид:
и будет иметь вид:
![]()
 1
1
![]()
![]() 0
0 ![]()
Рис.1
Из
чего следует, что если параметры кривой распределения первого типа будут
находиться в пределах ![]() , то мы будем
получать форму кривой распределения, изображенную на рис.1.
, то мы будем
получать форму кривой распределения, изображенную на рис.1.
Из пятидесяти рассмотренных выборок двадцать четыре имеют такую форму кривой распределения вероятностей.
Пример 2.
Рассмотрим другую выборку:
|
|
|
|
|
| 1 | 8,460199654 | 2 | Кривая распределения вероятностей первого типа. |
| 2 | 45,34087276 | 8 | |
| 3 | 18,07745451 | 5 | |
| 4 | 5,419406056 | 8 | Параметры кривой: |
| 5 | 18,67596108 | 6 | |
| 6 | 23,24656701 | 9 |
|
| 7 | 18,95143622 | 1 |
|
| 8 | 53,27426755 | 3 |
|
| 9 | 54,93095666 | 1 |
|
| 10 | 24,27284002 | 2 |
|
| 11 | 17,74883789 | 4 |
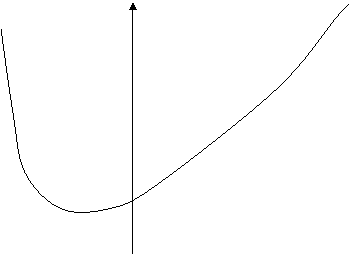
Кривая распределения вероятностей имеет в этом случае форму, показанную на рис. 2.
![]()
 1
1
![]() 0
0 ![]()
Рис.2
В
этом случае параметры кривой распределения будут: ![]() . И если
параметры кривой распределения другой выборки будут удовлетворять этим
неравенствам, то форма кривой распределения этой выборки будет похожа на рис.
2.
. И если
параметры кривой распределения другой выборки будут удовлетворять этим
неравенствам, то форма кривой распределения этой выборки будет похожа на рис.
2.
Этот случай встретился нам семь раз из пятидесяти.
Пример 3
|
|
|
|
|
| 1 | 3,881268442 | 7 | Кривая распределения вероятностей первого типа. |
| 2 | 1,343869925 | 17 | |
| 3 | 3,770335495 | 11 | |
| 4 | 2,860628724 | 9 | Параметры кривой: |
| 5 | 2,043179214 | 4 | |
| 6 | 1,447737217 | 10 |
|
| 7 | 2,43993476 | 13 |
|
| 8 | 1,658227324 | 8 |
|
| 9 | 3,98119396 | 16 |
|
| 10 | 1,391261339 | 5 |
|
Кривая распределения вероятностей имеет вид:
 |
1
![]()
![]() 0
0 ![]()
Рис. 3
Такой
будет форма кривой распределения вероятностей, если параметры ![]() . Эта форма
кривой встречается шестнадцать раз из пятидесяти.
. Эта форма
кривой встречается шестнадцать раз из пятидесяти.
§2. Алгоритм вычислений.
![]()
![]()

![]()
| Тип кривой распределения вероятностей |


|
Проверка условий для |
| æ Пирсона |

| Исходные данные |
|
|
|
|


| i |
 |
Заключение.
В дипломной работе были рассмотрены вопросы нахождения распределения вероятностей по заданным выборочным значениям случайной величины. В первой главе было рассмотрено решение дифференциального уравнения Пирсона, проклассифицированы с помощью æ критерия Пирсона, найдены типы кривых распределения вероятностей и параметры, соответствующие каждому типу.
Во второй главе был рассмотрен подход Чебышева к получению систем ортогональных полиномов, которые обладают свойством метода наименьших квадратов. Было рассмотрено применение способа Чебышева для нахождения кривой распределения вероятностей по обобщенному методу Грамма – Шарлье.
В третьей главе описывается алгоритмическое обеспечение нахождения кривых распределения вероятностей по методу Пирсона.
Результаты дипломной работы могут представлять большое значение для решения многих практических задач, так как часто возникает необходимость по экспериментальным данным оценить распределение вероятностей измеренной случайной величины.
Список литературы
Гмурман В.Е. Теория вероятности и математическая статистика. Учебное пособие для вузов. М.: Высшая школа, 1999
Джексон Д. Ряды Фурье и ортогональные полиномы. М.: Государственное издательство иностранной литературы, 1948
Митропольский А.К. Техника статистических распределений. М.: издательство “Наука”, 1971
Немчинов В.С. Полиномы Чебышева и математическая статистика. М.: издание Московской ордена Ленина сельскохозяйственной академии имени К.А. Тимирязева, 1946
Романовский В. И. Математическая статистика. Издательство Академии Наук УзССР, 1961
Суетин П.К. Классические ортогональные многочлены. М.: издательство “Наука”, 1976
Хинчин А. Я. Цепные дроби. М.: Государственное издательство физико-математической литературы, 1961
Хотимский В. И. Выравнивание статистических рядов по методу наименьших квадратов (способ Чебышева). М.: Государственное статистическое издательство, 1959