Реферат: Перспективные аспекты развития физико-топологических представлений о времени

И.В. Злобин, Член Финляндской Астрономической Ассоциации,Хельсинки, Финляндия

Время, как форма движения материи представляет собой детерминированную систему с жесткими причинно-следственными связями. Эти связи характеризуются устойчивой консеквентной сменой таких хронологических параметров, как - Прошлое, Настоящее и Будущее.

К разряду общих фундаментальных свойств Времени, принятых сегодня в физике, наиболее точно установленными являются: гомогенность и изотропность [1] .

Здесь и везде, термины: Время, Прошлое, Настоящее и Будущее, будем записывать с заглавной буквы там, где о них говорится, как о реальных физических факторах.

С точки зрения существующей реальности, разумно допустить, что Прошлое, Настоящее и Будущее могут коррелировать с понятием -спектральных параметров Времени. На "стреле" Времени [2] эти критерии группируются следующим образом: Будущему принадлежат точки Времени лежащие над Настоящим и Прошлым, Настоящее занимает промежуточное положение между областями Прошлого и Будущего, а Прошлое проецируется на ту часть на "стреле" Времени, которая располагается ниже зоны включающей точки Времени Настоящего и тем более точки Времени Будущего ( Рис. 1 ). Такая картина естественно непротиворечива, как в отношении континууальности Времени, так и с точки зрения наших оценок хронологических этапов, т.е., что есть - "вчера", "сегодня", "завтра".

С физической точки зрения целесообразно отметить, что в данном анализе не проводится разделение Будущего и Прошлого на хронологическое и каузальное. Специфика принятия такого решения заключается в том, что Хокинг и Эллис [2] показали: "... в физически реалистических решениях условие причинности и хронологическое условие эквивалентны". Таким образом, в данном исследовании оперируем моделью максимально приближенной к реальным макрофизическим процессам, т.е. начальные условия задаются базисом, основывающимся на необратимости Времени реального Мира [3].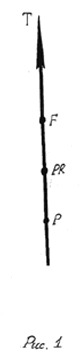

Для ясности понимания квинтэссенции предлагаемых ниже понятий и предложений необходимо ввести ряд обозначений. Необходимость этого шага продиктована тем, что в настоящее время трудно найти достаточно координальную программу иллюстрирующую физическую концепцию Времени.

Обозначим через Время n-измерений, т.е. множество всевозможных наборов п чисел с обычной топологией. Пусть  означает "нижнюю половину", т.е. область, в которой t < 0 (область  Прошлого - Р ). И пусть означает "верхнюю половину", которой t > 0 (область Будущего - F ). Тогда можно задать отображение Ф некоторого открытого множества на открытое множество  если координаты точки в Q' ^ является образом координат точки k в Q . Говоря об n-измерении Времени Т в начале абзаца мы естественным образом однозначно ожидаем, что на макро - и мегамасштабах окружающей нас физической реальности Время имеет одно измерение, т.е. n = 1 . И как следствие будет наблюдаться свертывание координат к виду a. Правда, пока открытым остается вопрос относительно существования многомерности у Времени на планковском уровне [4].

Зададим, так называемое универсальное множество Времени - множество, состоящее из всех элементов рассматриваемых в данной проблеме. В нашем случае тождественно Времен. Вместе с универсальным множеством имеет место набор, где - биективное отображение F и Р соответсвенно на такие открытые множества в Т1 , что

1) F, Р образуют покрытие, т.е.;

2) если не пусто ( заметим, что это условие выполняется, потому что пересечение множества Будущего и множества Прошлого формирует множество Настоящего - PR, т.е. = PR), то компазиция

,есть отображение некоторого открытого подмножества Т1 на открытое подмножество Т ( Рис. 2,3).

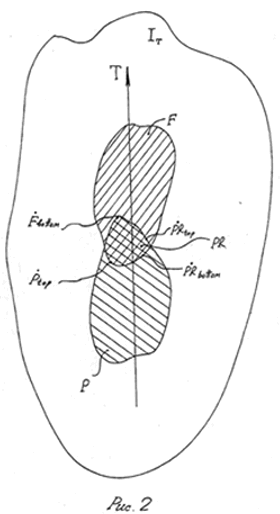
Здесь и всюду, примем такие сокращенные условные обозначения для Будущего - F (future), для Настоящего - PR (present), для Прогплого - Р (past). Следуя общепринятым математическим принципам введения понятия топологии, сформулируем критерии образующие конструкцию топологического Времени.

На универсальном множестве Времени группируется структура топологического Времени, если задано собрание вида { F, PR, Р } ее подмножеств, обладающее следующими свойствами:

1) собрание {F, PR, P} и пустое множество принадлежат; , 2) объединение любого числа множеств собрания { F, PR, Р } и пересечение любого конечного числа множеств собрания { F, PR, Р } принадлежат {F, PR, Р } .

Собрание {F, PR, Р }, удовлетворяющее условиям 1)и 2), называется топологией на универсальном множестве Времени. А значит, дублет - и { F, PR, Р } образуют топологическое Время .

Таким образом, можно сказать, что на универсальном множестве Времени доминируют множества: Будущего, Настоящего, Прошлого и пустое множество. В [2] мы находим определение Будущего и Прошлого, которое оценивается с точки зрения разделения их на хронологическое и причинное. Ниже сформулируем определения, касающиеся Прошлого, Настоящего и Будущего, в которых будут содержаться более расширенные сведения об этих Временных структурах.Определение 1.

Множество Будущего (F) - это множество всех точек принадлежащих этому множеству и лежащих на временной оси так, что они образуют открытое множество каждая точка, которого является внутренней (причем, где - точки множества); приэтом множество F имеет минорант, т.е. оно ограничено снизу. Тогда данное множество содержит минимальный элемент. В связи с этим, возможно указать нижнюю границу этого множества:

, где форма представляет собой множество всех граничных точек множества Будущего, являющихся элементами частично упорядочного множества, КОТОРЫЕ предшествуют любому элементу данного множества, ( Рис. 1,2).

Определение 2.

Множество Прошлого ( Р ) - это множество всех точек принадлежащих этому множеству и лежащих на временной оси так, что они образуют открытое множество каждая точка, которого является внутренней (причем

, где - точки множества); при этом множество Р имеет мажорант, I

т.е. оно ограничено сверху. Тогда согласно лемме Цорна [5] данное множетсво содержит максимальный элемент. В связи с этим, возможно указать верхнюю границу этого множества:, где форма представляет собой множество всех граничных точек множества Прошлого, являющихся элементами частично упорядочного множества, КОТОРОМУ предшествует любой элемент данного множества, (Рис. 1,2).

Определение 3.

Множество Настоящего ( PR ) - это множество всех точек С; принадлежащих тому множеству и полученных путем пересечения множеств Будущего и Прошлого,. Эти точки лежат на временной оси так, что образуют открытое множество каждая точка, которой является внутренней (причем, где - точки множества); приэтом множество PR - есть ограниченное множество, т. е. множество ограниченное сверху и снизу. В связи с этим, возможно указать мажорант и минорант для PR , т. е. два вида границ:

верхнию и нижнию, (Рис. 1,2).

На ( Рис.2 ) показана Венна ( J. Venn ) [5] диаграмма (графический способ изображения формул алгебры множеств), которая наглядно демонстрирует физический смысл выше указанных дефиниций. На этой диаграмме уверенно просматривается калибровка между границами множеств Прошлого, Настоящего и Будущего. Эта калибровка сведена в систему тождеств

 ( 1 )

Определение 4.

Минорант Настоящего накладывается на мажорант Прошлого и мажорант Настоящего соединяется с минорантом Будущего. Эти границы гладко сшиваются между собой, без разрывов.

Определившись по некоторым общим ключевым вопросам топологической интерпритации конструкции Времени [3], перейдем к анализу двух частных положений, которые тесным образом связаны с топологическим Временем.

Поскольку, с одной стороны, при задании топологического Времени мы руководствовались строгими принципами топологии, как одной из основных математических структур, а с другой стороны - оперируя реальной спецификой хронологической изменчивости в сложных и масштабных системах, то в связи с этим необходимо выяснить физическую сущность таких составных частей Временной топологии, как пустое множество и множество Настоящего PR .

Запишем следующие две формулировки.

Первая: показать условность существования на универсальном множестве Времени пустого множества и физически обосновать элиминировку этой категории на.

Вторая: представить аргументы в пользу существования переменного характера у Настоящего, которое выражается в том, что при общих физических оценках PR не входит в в явном виде.

Наиболее полное на наш взгляд, решение поставленных выше частных задач можно получить в том случае, если к ним применить алгоритмы алгебры Буля (G. Boole) [5], т.е. алгебры производящей теоретико-множественные операции над множествами. Эта алгебра имеет своеобразные законы действия, которые существенно отличаются от законов действия над числами.

Сформулируем такое предложение.

Предложение 1.

В физически реалистических условиях на универсальном множестве Времени не просматриваются области индетифицирующиеся с пустым множеством .

Дано:.Доказать:.

Доказательство:

1) Перепишем общее выражение для универсального множества Времени

 ( 2 )

2) В теории множеств всякое пустое множество можно представить, как пересечение некоторого множества и его дополнения. Под дополнением множества в алгебре Буля понимается множество всех элементов универсального множества не принадлежащих исходному множеству. Таким образом, легко записать тремя способами

 (3)

Вообще - то, запись пустого множества в виде триплета ( 3 ) не лишена целесообразности, поскольку мы должны, в силу существования топологии Времени, учитывать все три спектральных компаненты Времени и их дополнения.

3) Учитывая ( 3 ) перепишем ( 2 ) в виде

, (4.1)

, (4.2 )

, ( 4.3)

Здесь, весьма важным являтся тот факт, что в булевой алгебре при правилах действия над множествами, сведенных в равенства, необходимо строго соблюдать чередование, слева и справа, членов в этих выражениях.

4) Проанализируем формулу ( 4.1 )

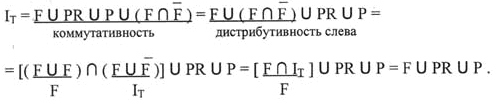
Что и требовалось доказать, т.е..

5) Рассмотрим равенство (4.2 )

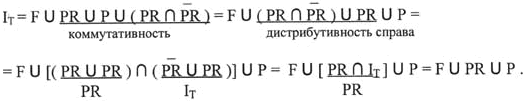
Доказали существование равенства вида

6) И, в заключении, проверим выражение (4.3 )

Получили финитный результат типа.

Проведем экспликацию полученных выше результатов применительно к реальным физическим условиям. Для этого, сначала, обратимся к определению; пустое множество - это множество, не содержащее ни одного элемента. Такого рода ситуация приводит к тому, что на универсальном множестве Времени пустое множество - вырезано. А это значит, что на оси Времени Т1 трудно выделить точки для подобных областей, которые имели бы конкретные координаты. Кроме этого, в алгебре множеств за пустым множеством закреплена функция нуля алгебры чисел, т.е. аддитивная операция с любым произвольно выбранным множеством не меняет этого множества. Таким образом, для процессов связанных с концепцией физического Времени, пустое множество выступает как нуль-момент Времени, т.е. соответствует такой точке, в которой отсчет Времени равен нулю. Существование такой точки можно, вероятно, прогнозировать только в системе координат коррелирующей с точкой начала раздувания Вселенной. На данном же этапе развития представлений о физических процессах окружающего нас Мира, начиная с уровня фундаментальных взаимодействий и кончая масштабами видимой части Вселенной, не возможно найти такую область, где бы реализовывалось выше указанное физическое явление.

Значит, достоверно и однозначно указать в естественном Времени точку (точки) эквивалентные не представляется возможным. Одноко, все же, мы должны сознавать, что условия топологического Времени способствуют тому, чтобы фигурировало бы в общей топологии Времени, как составная часть общего решения. Ведь, по сути дела, пустое множество вводится для того,чтобы мы могли говорить о множествах, как о системах априори существующих. Сформулируем такое предложение.

Предложение 2.

Универсальное множество Времени адекватно двум классам Временных множеств, которые пропорциональны только множеству Будущего F множеству Прошлого Р , а на множество Настоящего PR накладывается принцип переменности.

Проведем верификацию этого предложения.

Дано:.

Доказать: .

Доказательство: доказательство будем проводить для общего решения 1Т.

1) Поскольку и учитывая выражение ( 3 ) представим универсальное множество Времени в виде триады:

, (5.2)

, (5.2)

(5.3)

2) Исследуем вариант ( 5.1 )

Таким образом доказано, что выражение - существует .

3) Анализ записи ( 5.2 )

Перед доказательством, целесообразно сделать следующее замечание. Так как, Настоящее PR образовано пересечением Будущего и Прошлого, то легко представить, что дополнение множества Настоящего есть дополнение пересечений множеств Будущего и Прошлого, т.е..

Здесь доказанно, что универсальное множество Времени свободно от пустого множества и от множества Настоящего. 4) Разберем случай ( 5.3 )

Имеет место конечный результат, в котором отражено, что только объединение Будущего и Прошлого формирует универсальное множество Времени.

Заметим, что при доказательстве Предложений 1 и 2 сознательно приводятся полные записи алгебраических преобразований. Это необходимо делать, по-скольку нужна полная ясность при использовании методики Булевой алгебры применительно к композиции существующей между Прошлым, Настоящим и Будущим.

Представленная выше серия доказательств, естественно, требует самой прямой увязки с физической реальностью окружающего нас мира. И поэтому посмотрим каким образом можно использовать полученные результаты.

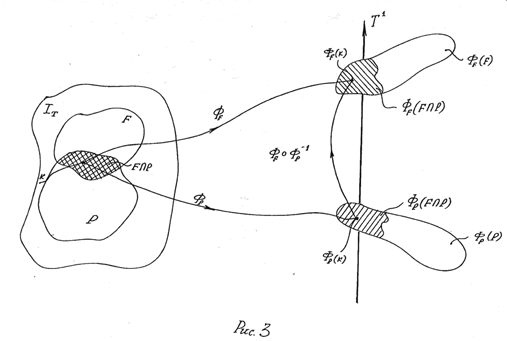
Для начала обратимся к Рис. 3 . Эта диаграмма схожа по своей форме с той, которая дается Хокингом и Эллисом в [2] . Но между ними есть принципиальное различие. Если в [2] диаграмма создается главным образом для пространства, то здесь схема стротся в ракурсе Временных отношений.

Итак, на Рис. 3 , в левой части фигурирует универсальное множество Времени. В иньективны множества Будущего, Настоящего и Прошлого, которые являются подмножествами При этом должен соблюдаться принцип каузальности и условие пересечения F и Р . Выберем на множестве Настоящего PR произвольную точку k , где . В связи с тем, что пересечение множеств Будущего и Прошлого приводит к возникновению множества Настоящего, то если.

В правой же части схемы показано Время n= 1 -измерений. Посмотрим, каким образом трансформируется левая часть при отображении на.

Первый шаг: за счет существования оператора взаимо-однозначного отображения происходит выделение множества и области. К тому же, теперь, координатой точки k является координата . Причем.

Второй шаг: при действии оператора взаимно-однозначного отображения наблюдается образование множества и области;. При этом, координатой точки k является координата. Где.

Третий шаг: композиция обеспечивает последовательную транспозицию координаты на координату, области на область и множества на множество, где -есть обратное отображение.

Мы видим, что на преобладают только два полных множества и, т.е. множества Будущего и Прошлого. Множество Настоящего PR , как оно представлено на универсальном множестве Времени в левой части Рис. 3, в явной форме на не экстраполируется. Действительно, одна часть PR принадлежит F , т.е. область, а другая принадлежит Р , т.е. область. Другими словами, множество Настоящего распадается на две составные части. Эти части ассоциируются, как подмножества множеств Прошлого и Будущего. Наблюдается, своего рода, переменность, т.е. реально мы можем говорить об условно заданной Временной характеристике.

В связи с этим, весьма проблематично однозначно указать в реальном физическом Времени область эквивалентную Настоящему, и которая, к тому же была бы принята за точную копию системы отсчета, относительно которой эвентуально было бы указать жестко детерминированные области Прошлого и Будущего. В условиях окружающей нас действительности не представляется возможным отождествить такое решение. Хорошим примером в подтверждение выше сказанному служит принцип задания Настоящего методом хронологической градации. Где под хронологической градацией подразумеваются известные шкалы времени, например: секундная, минутная, часовая и т.д.. В зависимости от того, какие задаются начальные условия (шкалы) для, где - шкала Времени, таким будет и выбор условия существования Р и F . Причем, выбор для PR весьма неоднозначен и зависит от масштаба физических систем.

Отметим так же, что в силу переменной аппроксимации PR , данный спектральный параметр Времени будет иметь нечеткую фиксацию границ и на.

Таким образом, универсальное множенство Времени (, Время n-измерений) в физически реалистических решениях должно строго оставаться в качестве формы, трансформирующйся в аддитивность двух доминирующих во Времени совокупностей - Прошлого и Будущего.

И все же, хотя Настоящее и имеет тендентность к неопределенной структуре, в нынешних условиях физика достаточно успешно работает с этими параметром. И на уровне сегодняшних физических представлений мы не подходим строго к описанию этой Временной области.

Основная задача данного исследования, с одной стороны, заключается в том, чтобы хотя бы в первом приближении разобраться в физической сущности тех известных характеристик, которые однозначно связаны с хронологией; а с другой - опробывать вероятный математический аппарат, который мог бы быть использован в качестве инструмента для описания действительных Временных процессов.

Кратко, резюмируем полученные в работе выводы: 1) выдвинуты аргументы в пользу того, что Время, как физическая система, имеет определенный набор спектральных параметров - это Будущее, Настоящее и Прошлое; 2) вводится понятие топологического Времени; 3) даются расширенные определения Прошлому, Настоящему и Будущему; 4) выделено, что Временные спектральные параметры имеют границы и устанавливается их взаимное соответствие по отношению друг к другу; 5) используя алгоритмы алебры Буля производится доказательство предложений, в которых предусматривается, что сводится к унитарности только Будущего и Прошлого, а Настоящее попадает под действие принципа переменности. А так же, что не может существовать на универсальном множестве Времени в явном виде.

В заключение, хотелось бы отметить, что сегодня на повестку дня остро встает вопрос о необходимости самого серьезного обращения фундаментальной физике к конструктивной разработке физических основ Времени. В будущем, мы можем столкнуться с тем, что у нас не найдется нужных физических наработок в отношении понимания природы Времени. Это может привести к определенного рода затруднениям в некоторых областях фундаментальной физики.

Список литературы

1. Л.Д.Ландау, Е. М. Лифшиц, Механика, Изд. 3, М, Наука, 1973.

2. С. Хокинг, Дж. Эллис, Крупномасштабная структура пространства времени, Мир, М., 1977.

3. С. М. Коротаев, Земля и Вселенная, 2,1989, с. 53.

4. А.Д.Сахаров, - ЖЭТФ, 1984, т. 87, с. 375.

5. Ю. Я. Каазик, Математический словарь, Валгус, Таллин, 1985 .