Курсовая работа: Спиральная антенна
СОДЕРЖАНИЕ.
1.Режимы излучения спиральной антенны 2
2.Расчетные соотношения для цилиндрической спиральной антенны 5
3.Плоская арифметическая спиральная антенна 8
4.Равноугольная (логарифмическая) спиральная антенна 11
5.Пример расчета цилиндрической спиральной антенны 14
Список использованной литературы 16
 1. Режимы излучения спиральной антенны.
1. Режимы излучения спиральной антенны.
1.1. Спиральная антенна представляет собой свернутый в спираль провод (1), который питается через коаксиальный фидер (2) (рис. 1, а). Внутренний провод фидера соединяется со спиралью, а внешняя оболочка фидера — с металлическим диском (3). Последний служит рефлектором, а также препятствует проникновению токов с внутренней на наружную поверхность оболочки фидера. Спираль может быть не только цилиндрической, как на рис. 1, а, но и конической (рис. 1, в) и плоской (рис. 7) или выпуклой.
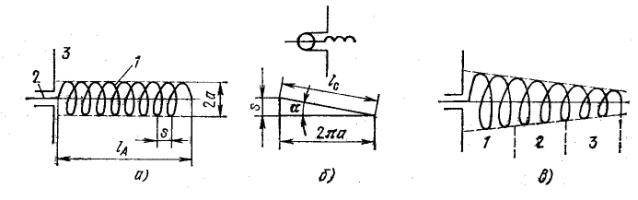
Рис.1. Спиральные антенны:
а - цилиндрическая; б – развёрнутый виток; в – коническая.
Цилиндрическая спиральная антенна характеризуется следующими геометрическими размерами: радиусом а,
шагом s, длиной одного витка![]() , числом витков p,
длиной по оси
, числом витков p,
длиной по оси ![]() , углом подъема
, углом подъема .
Как видно из схемы антенны и изображения развернутого витка спирали (рис. 1, б), между размерами антенны имеются следующие зависимости:
![]() ,
, ,
![]()
1.2. Спиральные антенны используются на УКВ в режиме бегущих волн с осевым излучением и вращающейся поляризацией. Такой режим требует определенных соотношений между размерами антенны и длиной волны. Выявим эти соотношения.
 Ток высокой частоты, проходя но спирали, вызывает
излучение электромагнитных волн. Достаточно десяти-одиннадцати витков, чтобы вся подводимая к антенне энергия излучалась в пространство и не происходило
отражения волн от конца спирали. Такая бегущая волна тока распространяется вдоль провода спирали с фазовой скоростью
Ток высокой частоты, проходя но спирали, вызывает
излучение электромагнитных волн. Достаточно десяти-одиннадцати витков, чтобы вся подводимая к антенне энергия излучалась в пространство и не происходило
отражения волн от конца спирали. Такая бегущая волна тока распространяется вдоль провода спирали с фазовой скоростью , т. е., с замедлением
![]() .
.
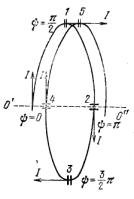
Рис.2.Виток спиральной антенны
Волна проходит один виток (от сечения 1 к сечению5 на рис. 2) за время.Электромагнитные волны, возбуждаемые током спирали, распространяются в воздухе со скоростью с и
длиной волны
![]() .
.
Если бы все витки сливались, то достаточно было установить время, равным периоду колебаний
![]() , т.
е.
, т.
е.![]() , чтобы поля любой пары противоположных элементов (1-3,2-4)
спирали совпадали по фазе и полностью складывались в точках оси 0'0", которая равноудалена от контура витка. Это объясняется тем, что в пределах
одного витка амплитуды тока практически одинаковая, а различие в фазе на угол
, чтобы поля любой пары противоположных элементов (1-3,2-4)
спирали совпадали по фазе и полностью складывались в точках оси 0'0", которая равноудалена от контура витка. Это объясняется тем, что в пределах
одного витка амплитуды тока практически одинаковая, а различие в фазе на угол в диаметрально противоположных сечениях витка (1-3, 2-4) компенсируется противоположным
направлением токов в них.
В случае спирали цилиндрической формы с шагом s условие максимального осевого излучения
формулируется несколько иначе: за время прохождения тока по витку электромагнитная волна должна пройти в воздухе расстояние большее, чем длина волны, на шаг s:
![]() ; соответственно
; соответственно
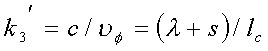 (1)
(1)
При таком коэффициенте замедления токи в любых двух сечениях, расположенных под углом 90° (например, в 1 и 2, 2 и 3, 3 и 4, 4 и 5), вызывают на оси О'О" поля, которые сдвинуты по фазе на 90°, и волны, которые поляризованы под углом 90°. В результате сложения этих линейно-поляризованных волн получаются волны с круговой поляризацией.
1.3. Опытным путем установлено, что с увеличением длины волны фазовая скорость
![]() уменьшается, а коэффициент замедления
уменьшается, а коэффициент замедления увеличивается во столько же раз. Благодаря этому условие осевого излучения (1) поддерживается в широком диапазоне волн:
|
|
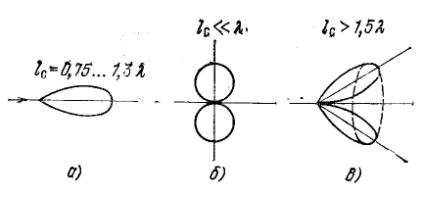
Рис.3.ДН цилиндрической спиральной антенны
при различной длине витка спирали
При длине витка ![]() набег фазы в 360°
происходит при прохождении волной тока нескольких витков спирали. При этом антенна уподобляется электрически малой рамке из N витков провода, которая имеет ДН в виде восьмерки с
максимумами излучения в плоскости, перпендикулярной оси спирали (рис. 3, б). Если
набег фазы в 360°
происходит при прохождении волной тока нескольких витков спирали. При этом антенна уподобляется электрически малой рамке из N витков провода, которая имеет ДН в виде восьмерки с
максимумами излучения в плоскости, перпендикулярной оси спирали (рис. 3, б). Если, то на одном витке спирали укладывается две, три и более волн, а это приводит к наклонному излучению и конусной форме пространственной
ДН (рис. 3, в).
1.4. Наиболее выгодный режим — осевого излучения, который, как известно, требует длины витка и обеспечивает полосу пропускания
. Эта полоса может быть значительно расширена путем перехода к конической антенне (рис, 1, б),
в которой участок (2) со средней длиной витка
![]() удовлетворяет условию
удовлетворяет условию, а крайние участки (1, 3) с большими (
) и меньшими (
![]() ) длинами витков удовлетворяют аналогичным условиям, но для
максимальной
) длинами витков удовлетворяют аналогичным условиям, но для
максимальной ![]() и минимальной
и минимальной длин волн рабочего диапазона:
![]() ,
,. В зависимости от рабочей длины волны
интенсивно излучает только одна из зон спирали и только этой активной зоной определяется острота ДН.
2. Расчетные соотношения для цилиндрической спиральной антенны.
2.1. Чтобы получить максимальный КНД, нужно установить оптимальный коэффициент замедления, при котором в направлении оси спирали 0'0" (рис. 2) поля первого и последнего витков находятся в противофазе. Иначе говоря,
необходимо дополнить условие (1) задержкой волны тока спирали на полупериод Т/2, а в каждом витке ее — на
:
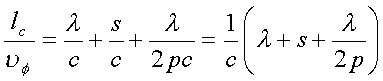 .
.
Отсюда находим оптимальный коэффициент замедления вдоль провода спирали:
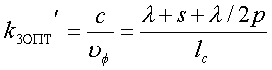 , (2)
, (2)
При этом, правда, получается эллиптическая поляризация, но так как, то коэффициент
![]() весьма незначительно отличается
от
весьма незначительно отличается
от 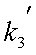 и полученную поляризацию можно считать круговой. Полагая
и полученную поляризацию можно считать круговой. Полагая = 1,2 ... 1,3, определим из выражения (2) угол подъема спирали, соответствующий оптимальным условиям работы антенны
 :
:
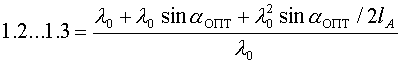
Отсюда
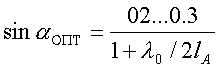 , (3)
, (3)
Длина спирали ![]() подбирается в соответствии с оптимальным коэффициентом
замедления вдоль оси спирали
подбирается в соответствии с оптимальным коэффициентом
замедления вдоль оси спирали![]() . При
. При =1,2…1,3 имеем
![]() , что соответствует углу подъема спирали
, что соответствует углу подъема спирали =12 ... 16° и числу витков р = 5 ... 14.
2.2. Рассматривая каждый виток спирали как элементарный излучатель с фазовым центром на оси 0'0",
определяем функцию направленности антенны ![]() как произведение функции
направленности одного витка
как произведение функции
направленности одного витка ![]() на множитель решетки
из р элементов
на множитель решетки
из р элементов![]() . Так как р велико, а направленность одного витка
мала, то принимаем
. Так как р велико, а направленность одного витка
мала, то принимаем![]() . В результате имеем
. В результате имеем
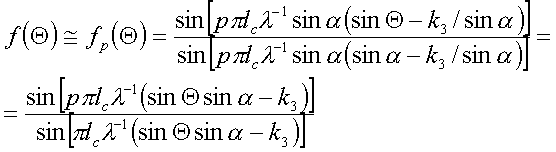 (4)
(4)
Угол ![]() , как и прежде, отсчитывается от перпендикуляра к оси линейной
решетки.
, как и прежде, отсчитывается от перпендикуляра к оси линейной
решетки.
2.3. Для спиральных антенн оптимальных размеров опытным путем установлены следующие формулы:
ширина диаграммы направленности
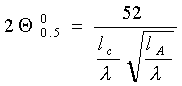 , (5)
, (5)
коэффициент направленного действия
![]() , (6)
, (6)
входное сопротивление
![]() , (7)
, (7)
2.4. Итак, цилиндрические и конические спиральные антенны широкополосные с осевым излучением волн круговой поляризации. Направленность цилиндрических спиралей средняя, а конических — ниже средней (не вся спираль участвует в излучении на данной частоте), но последние обладают большей диапазонностью. Применяются и те и другие как самостоятельные антенны в диапазонах дециметровых а метровых волн, а также как облучатели антенн сантиметровых волн.
3. Плоская арифметическая спиральная антенна.
3.1. В процессе развития радиотехники все больше требуются антенно-фидерные устройства, рассчитанные на работу в очень широком диапазоне частот и притом без всякой перестройки. Частотная независимость таких антенно-фидерных устройств основана на принципе электродинамического подобия.
Этот принцип состоит в том, что основные параметры антенны (ДН и входное сопротивление) остаются
неизменными, если изменение длины волны ![]() сопровождается прямо
пропорциональным изменением линейных размеров активной области антенны. При соблюдении данного условия антенна может быть частотно-независимой в
неограниченном диапазоне волн. Однако размеры излучающей структуры конечны и рабочий диапазон волн любой антенны тоже ограничен.
сопровождается прямо
пропорциональным изменением линейных размеров активной области антенны. При соблюдении данного условия антенна может быть частотно-независимой в
неограниченном диапазоне волн. Однако размеры излучающей структуры конечны и рабочий диапазон волн любой антенны тоже ограничен.
 Из этой группы антенн рассмотрим плоские
арифметические и равноугольные спирали и логарифмически-периодические антенны.
Из этой группы антенн рассмотрим плоские
арифметические и равноугольные спирали и логарифмически-периодические антенны.
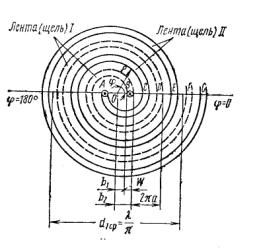
Рис.4. Арифметическая спираль
3.2. Арифметическая спираль выполняется в виде плоских металлических лент или щелей в металлическом экране (рис. 4). Уравнение этой спирали в полярных координатах
![]()
где ![]() — радиус-вектор,
отсчитываемый от полюса О; а — коэффициент, характеризующий приращение радиус-вектора на каждую единицу приращения полярного угла
— радиус-вектор,
отсчитываемый от полюса О; а — коэффициент, характеризующий приращение радиус-вектора на каждую единицу приращения полярного угла ; b — начальное значение радиус- вектора.
Спираль может быть двухзаходной, четырёхзаходной и т. д. Если спираль двухзаходная, то для ленты
(щели) /, показанной штриховыми линиями, угол ![]() отсчитывается от
нуля, а для ленты //, показанной сплошными линиями, — от 180°, т. е. спираль образована совершенно идентичными лентами, повернутыми на 180° друг относительно друга.
отсчитывается от
нуля, а для ленты //, показанной сплошными линиями, — от 180°, т. е. спираль образована совершенно идентичными лентами, повернутыми на 180° друг относительно друга.
Начальные точки ленты / соответствуют радиус-векторам, которые обозначим
![]() и
и . Следовательно, ширина ленты
![]() . Описав один оборот
. Описав один оборот, лента занимает положение D, в котором радиус-вектор больше начального на
. На этом отрезке ВD размещаются две ленты и два зазора, и если ширина их одинаковая, то
, Отсюда определяем коэффициент
![]() .
.
3.3. Питание спирали может быть противофазным, как на рис. 4, или синфазным. В первом случае токи через
зажимы А, В, соединяющие ленты с фидером, имеют противоположные фазы. Путь тока в ленте / больше, чем в ленте //, на полвитка. Например, в сечении СD лента // попадает, описав полвитка, а лента / — один
виток, в сечение ЕF—соответственно полтора и два витка и т. д. Поскольку длина витка по мере развертывания спирали возрастает,
увеличивается расхождение фазы токов в лентах. Обозначив средний диаметр витка находим сдвиг по фазе, соответствующий длине полувитка:
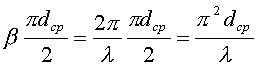
Если к этому прибавить начальный сдвиг, равный ![]() , то получим результирующее расхождение по фазе токов в
смежных элементах двухпроводной линии
, то получим результирующее расхождение по фазе токов в
смежных элементах двухпроводной линии
![]()
За счет второго слагаемого угол ![]() отличен от
отличен от , а в таких условиях электромагнитные волны излучаются, даже если зазор между лентами мал по сравнению с длиной волны.
Интенсивно излучает только та часть спирали, в которой токи смежных элементов обеих лент совпадают по фазе:
![]()
Подставляя ![]() , находим, что средний диаметр первого «резонансного» кольца
, находим, что средний диаметр первого «резонансного» кольца
![]() , а периметр этого кольца
, а периметр этого кольца .Средний диаметр и периметр второго (k=2), третьего (k=3) и т. д. «резонансных» колец соответственно в три, пять,
... раз больше. Так как излучение радиоволн спиралью вызывает большое затухание тока от ее начала к концу, то интенсивно излучает только первое резонансное
кольцо, а остальная, внешняя часть спирали как бы «отсекается» {явление отсечки излучающих токов}.
3.4. Активная часть спирали представляет наибольший интерес и по другой причине. Затухание тока, вызванное
излучением, настолько велико, что отражение от конца спирали практически отсутствует, т. е. ток в спирали распределяется по закону бегущих волн. К тому
же периметр первого резонансного кольца равен длине волны ![]() . В таких условиях, как показано в п. 1, происходит осевое
излучение с вращающейся поляризацией, которое в данном случае наиболее желательно.
. В таких условиях, как показано в п. 1, происходит осевое
излучение с вращающейся поляризацией, которое в данном случае наиболее желательно.
Диаметр спирали должен быть достаточно велик, чтобы на максимальной волне диапазона сохранилось первое «резонансное» кольцо (
),а с уменьшением длины волны это кольцо должно сжиматься до тех пор (
) , пока оно еще может полностью разместиться вокруг узла питания. Тогда в пределах
отношение среднего периметра первого «резонансного» кольца
к длине волны
![]() остается постоянным и
тем самым выполняется основное условие сохранения направленных свойств антенны в широком диапазоне волн
остается постоянным и
тем самым выполняется основное условие сохранения направленных свойств антенны в широком диапазоне волн Правда, направленность арифметической спирали невелика (
60 ... 80°), поскольку в излучении волн участвует, по существу, только та часть спирали, которая имеет средний периметр, равный
.
Второе условие получения диапазонной антенны—постоянство входного сопротивления — достигается здесь тем,
что спираль работает в режиме бегущей волны тока. Это сопротивление активное (100—200 Ом). При питании от коаксиального фидера ( Ом) согласование производят ступенчатым или плавным трансформатором.
3.5. Спираль излучает по обе стороны своей оси. Чтобы сделать антенну однонаправленной, ленточную спираль
помещают на диэлектрической пластине толщиной ![]() , другую сторону которой металлизируют. Если же спираль
щелевая, то ее вырезают на стенке металлического короба; тогда противоположная стенка короба играет роль отражающего экрана, а сам короб является
резонатором. Чтобы уменьшить его глубину, короб заполняют диэлектриком.
, другую сторону которой металлизируют. Если же спираль
щелевая, то ее вырезают на стенке металлического короба; тогда противоположная стенка короба играет роль отражающего экрана, а сам короб является
резонатором. Чтобы уменьшить его глубину, короб заполняют диэлектриком.
Одна из типовых спиралей имеет диаметр 76 мм, выполнена на пластине из эпоксидного диэлектрика, снабжена
резонатором глубиной 26 мм, работает в диапазоне волн ![]() 7.5 ... 15 см при
7.5 ... 15 см при , ширине диаграммы направленности 2
' = 60... 80° и коэффициенте эллиптичности в направлении максимума главного лепестка менее 3 дБ, т. е. практически поляризацию можно
считать круговой. Плоские спиральные антенны удобно изготовлять печатным способом на тонких листах диэлектрика с малыми потерями на высоких частотах.
4. Равноугольная (логарифмическая) спиральная антенна.
4.1. Широкодиапазонность антенн такого вида основана на том, что если отношение линейных размеров излучателя к длине волны остается постоянным и излучающая структура полностью определяется ее полярными углами, то направленность антенны оказывается абсолютно независимой от частоты.
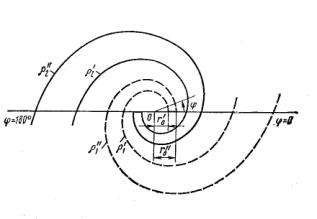
Рис.5. Логарифмическая спираль
Равноугольная спираль (рис. 5) строится в полярных координатах по уравнению
![]()
где ![]() — радиус-вектор в
начале спирали (
— радиус-вектор в
начале спирали (![]() ); а — коэффициент,
); а — коэффициент,
определяющий степень увеличения радиус-вектора с увеличением полярного угла .
Двухзаходная спираль образуется двумя проводниками или щелями, но в отличие от архимедовой
спиральной антенны толщина их непостоянна и возрастает с увеличением угла . Пусть начальный радиус-вектор на внутренней границе 1-го проводника равен
и на внешней
![]() . Тогда уравнениями граничных спиралей являются
. Тогда уравнениями граничных спиралей являются
![]() (8)
(8)
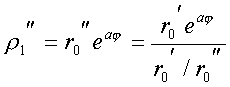 . (9)
. (9)
4.2. Для оценки диапазонности логарифмической спирали исследуем зависимость отношения от угла
![]() . Числитель дроби
. Числитель дроби ,а так как
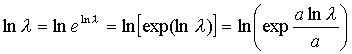 ,
,
то знаменатель дроби и искомое отношение 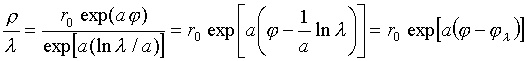 ,(10)
,(10)
где  . Следовательно, изменение длины волны вызывает только
смещение активной области спирали на некоторый угол
. Следовательно, изменение длины волны вызывает только
смещение активной области спирали на некоторый угол ![]() , а отношение
, а отношение и направленное действие антенны от этого не меняются. Если бы спираль была бесконечной, то
диапазонность антенны была безграничной, но реальная антенна имеет конечную
длину и эффективно работает в ограниченном, хотя и очень широком диапазоне волн
![]() ,причем
,причем определяется максимальной длиной спирали, а
— минимальными размерами узла питания.
 4.3. Логарифмическая спираль работает в режиме бегущих
волн (вследствие излучения ток затухает к концу спирали), и ее входное сопротивление
4.3. Логарифмическая спираль работает в режиме бегущих
волн (вследствие излучения ток затухает к концу спирали), и ее входное сопротивление Ом.
 Рис.6. Щелевая плоская логарифмическая
спиральная
Рис.6. Щелевая плоская логарифмическая
спиральная
антенна
Типовая щелевая логарифмическая спираль (рис. 6) имеет максимальную длину ветви 42,3 см, начальный
радиус 0,51 см и коэффициент ![]() = 0,303. Антенна
излучает волны с вращающейся поляризацией в диапазоне
= 0,303. Антенна
излучает волны с вращающейся поляризацией в диапазоне ![]() см и
см и не превышает двух при питании спирали от 50-Ом коаксиального кабеля. Параметры антенны находятся в
допустимых пределах даже при двадцатикратном изменении длины волны.
5.Пример расчета спиральной цилиндрической антенны.
Для построения диаграммы направленности антенны, пользуясь экспериментальными данными исследования спиральных антенн [1.Рис.1.3.XXV.], вычисляю по формулам (4) – (7) функцию направленности антенны.
![]()
Учитывая:
подставим все значения в формулу (4):
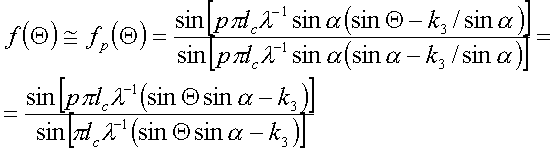 .
.
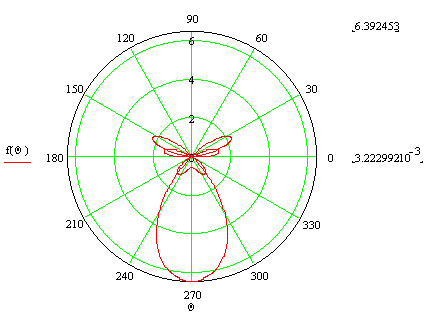 |
Используя приложение ”MathCAD 7 professional” получил следующий вид диаграммы направленности антенны:
.
По формуле 5 рассчитываю ширину диаграммы направленности:
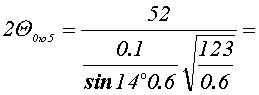 21.586.
21.586.
Коэффициент направленного действия :
 70.768.
70.768.
Входное сопротивление:
![]()
Итак, цилиндрические и конические спиральные антенны широкополосные с осевым излучением волн круговой поляризации. Направленность цилиндрических спиралей средняя, а конических — ниже средней (не вся спираль участвует в излучении на данной частоте), но последние обладают большей диапазонностью. Применяются и те и другие как самостоятельные антенны в диапазонах дециметровых и метровых волн, а также как облучатели антенн сантиметровых волн.
Список использованной литературы.
1.Айзенберг Г.З. Антенны ультракоротких волн . «Связьиздат»,М.1957.700 с
2.Лавров А.С.,Резников Г.Б. Антенно-фидерные устройства. «Сов.радио»,М.,1974,368 с.
3.Белоцерковский Г.Б. Основы радиотехники и антенны.В 2-х ч.
Ч. 2.Антенны-М.:Радио и связь,1983-296с.