Доклад: Теория отображений

Отобразить верхнюю половину плоскости с разрезами по отрезкам 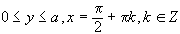на верхнюю полуплоскость.

Решение:

Отображение

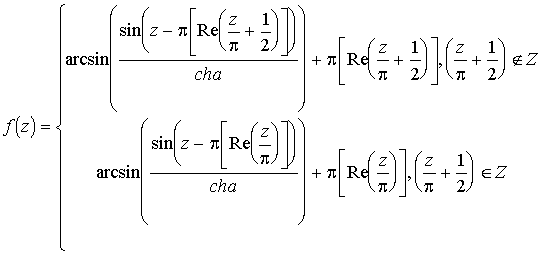
отображает верхнюю полуплоскость с разрезами на верхнюю полуплоскость без разрезов (под операцией взятия в квадратные скобки надо пономать взятие целой части от числа). Докажем это:

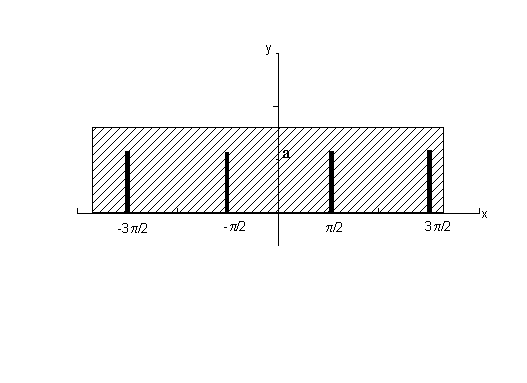
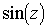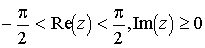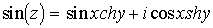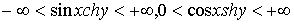Рассмотрим отображение из полосы полуплоскости сразрезами в полуплоскость без разрезов. (*) совершенно очевидно ,что в нашем случае . То есть, мы получаем верхнюю полуплоскость без действительной оси. Рассмотрим образ луча .

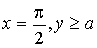Подставляя в формулу (*) значения z на луче мы получим в образе луч, лежащий на действительной оси 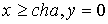. В результате мы получили, что образом полосы 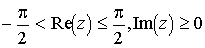(1) является .

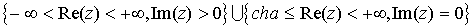Если на полосу 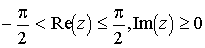плоскости без разреза подействовать отображением sin(Z) то в образе получим такое множество 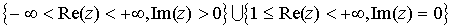(2). Применив отображение 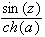к полосе(1) с разрезом в образе получим множество (2).

Поэтому функция 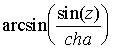отображает полосу 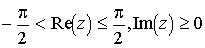с разрезом в полосу 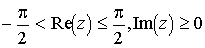без разреза.

Продолжим эту функцию на всю полуплоскость с разрезами. Рассмотрим функцию 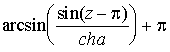заданную в полосе 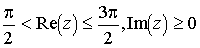с разрезом.

Функция отображает эту полосу на полосу 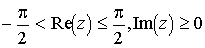без разреза.

И тогда отображение 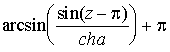отображает полосу 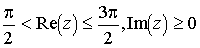без разреза.

Проверим является ли функция 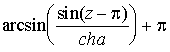аналитическим продолжением функции 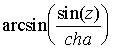. Для этого применим теорему:

Пусть функция 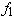аналитична в области и функция аналитична в области 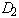. И области и 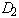имеют общий фрагмент граници 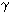. Если функции на 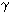совпадают то функция является аналитическим продолжением функции 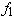в область .

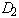Естественно функци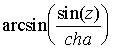и и 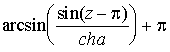совпадают на луче .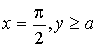

Поэтому функция 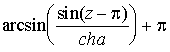является аналитическом продолжением функции 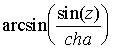на полосу .

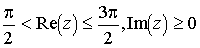Совершенно аналогично мы можем продолжмть функцию на всю верхнюю полуплоскость с вырезами. И в результате получим функцию: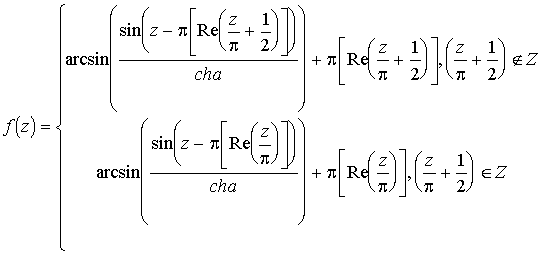

отображающую верхнюю полуплоскость с вырезами на верхнюю полуплоскость без вырезов.