Реферат: Экстремумы функций многих переменных
Министерство общего и высшего образования Российской Федерации
Иркутский Государственный Технический Университет
Кафедра ВЫСШЕЙ МАТЕМАТИКИ
Реферат
На тему: “Экстремумы функций многих переменных”
Выполнил:
Студент группы ТЭ-97-1
Мартынов Ф.О.
Проверила:
Преподаватель кафедры
Седых Е.И.
Иркутск 1998
План реферата:
1. Понятие экстремума........................... 2
2. Необходимые условия экстремума.. 3
3. Достаточные условия экстремума... 6
4. Локальные экстремумы.................... 8
5. Условные экстремумы...................... 9
Экстремумы функций многих переменных.
Для начала рассмотрим необходимые условия экстремума функции, также определим понятие экстремума. Начнем с понятия экстремума:
Положим, что имеется некоторая функция с двумя переменными 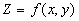
Определение: Точка 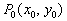 называется точкой экстремума (максимума или минимума)
называется точкой экстремума (максимума или минимума)
функции 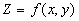 , если
, если 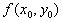 есть соответственно наибольшее или наименьшее значение функции
есть соответственно наибольшее или наименьшее значение функции 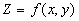 в некоторой окрестности точки
в некоторой окрестности точки 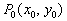 .
.
При этом значение 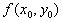 называется экстремальным значением функции (соответственно максимальным или минимальным). Говорят также, что функция
называется экстремальным значением функции (соответственно максимальным или минимальным). Говорят также, что функция 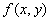 имеет в точке
имеет в точке 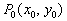 экстремум (или достигает в точке
экстремум (или достигает в точке 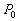 экстремума).
экстремума).
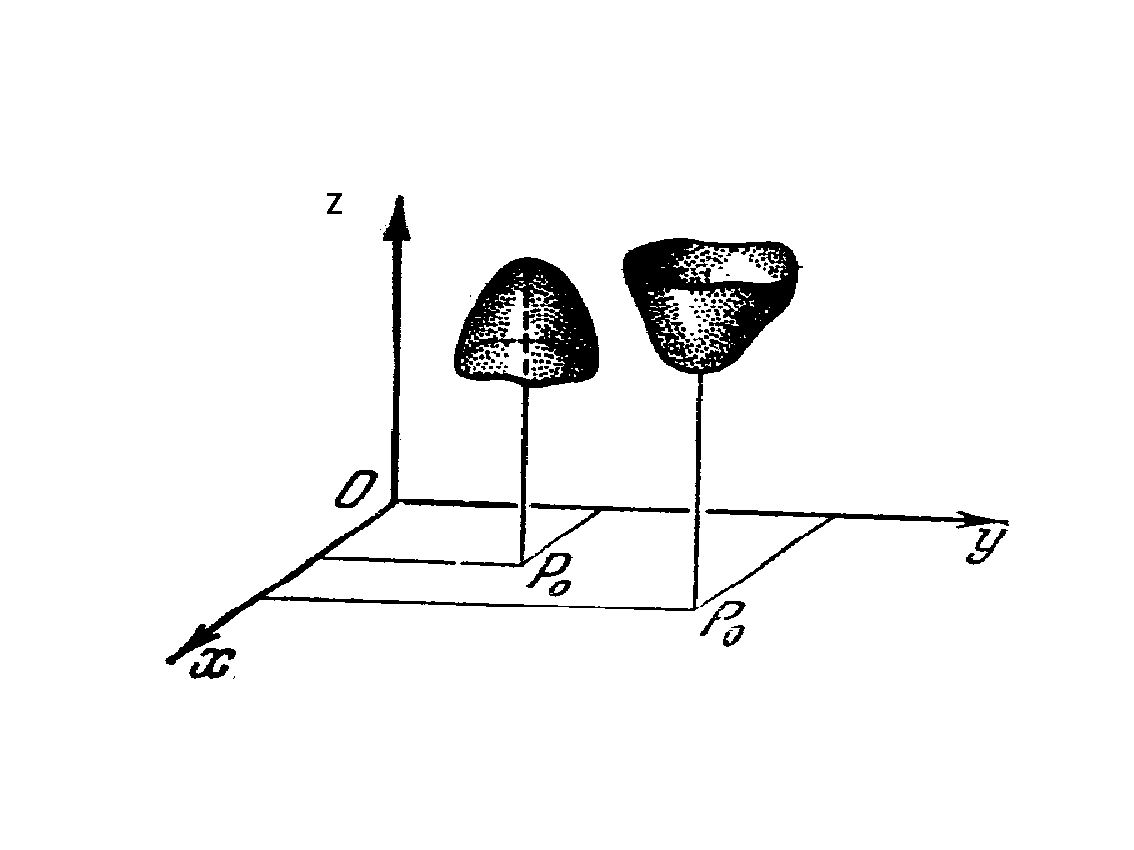
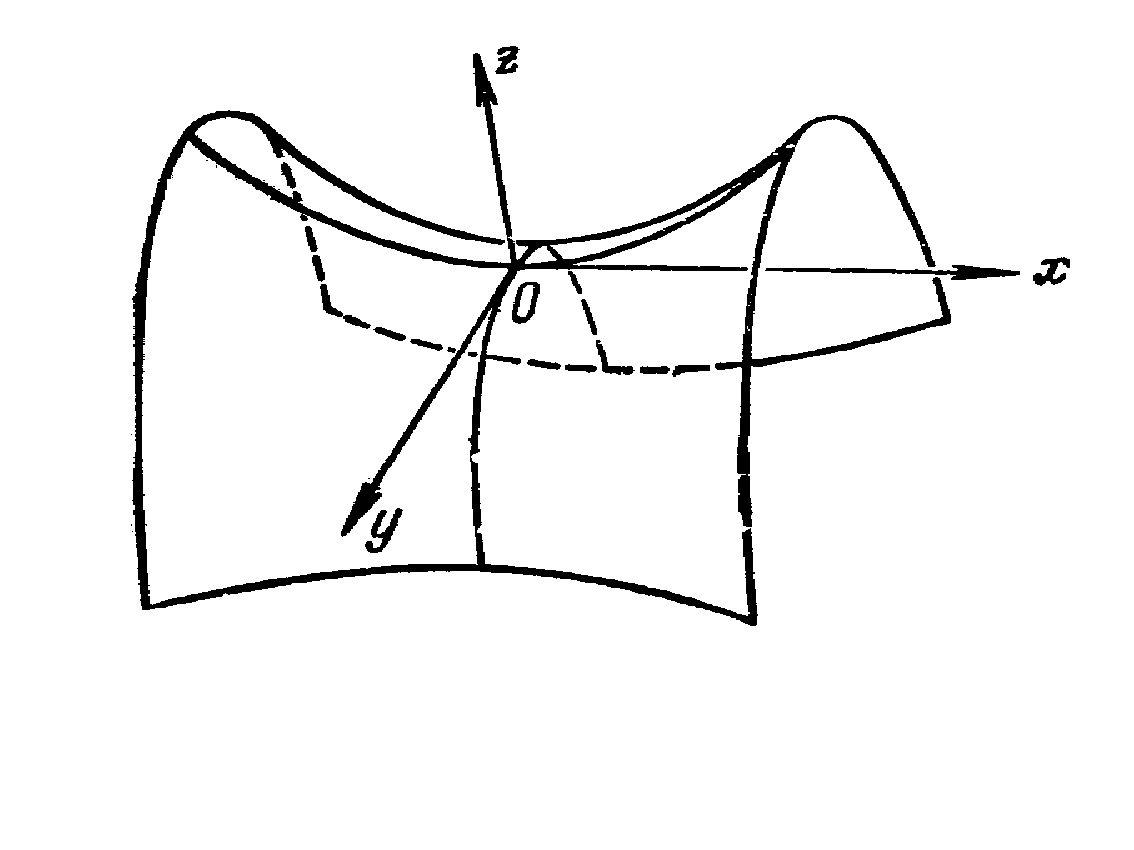
Заметим, что в силу определения точка экстремума функции лежит внутри области определения функции, так что функция определена в некоторой (хотя бы и малой) области, содержащей эту точку. Вид поверхностей, изображающих поверхности функций в окрестности точек экстремума показан на рис. 1.
Теперь установим необходимые условия, при которых функция 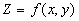 достигает в точке
достигает в точке 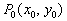 экстремума; для начала будем рассматривать только дифференцируемые функции.
экстремума; для начала будем рассматривать только дифференцируемые функции.
Необходимый признак экстремума: Если в точке 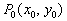 дифференцируемая функция
дифференцируемая функция 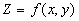 имеет экстремум, то ее частные производные в этой точке равны
имеет экстремум, то ее частные производные в этой точке равны
нулю:
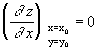 ,
, 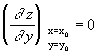 .
.
Доказательство: Допустим, что функция 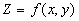 имеет в точке
имеет в точке 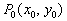 экстремум.
экстремум.
Согласно определению экстремума функция 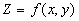 при постоянном
при постоянном 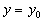 , как функция одного
, как функция одного 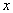 достигает экстремума при
достигает экстремума при 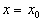 . Как известно, необходимым условием для этого является обращение в нуль производной от функции
. Как известно, необходимым условием для этого является обращение в нуль производной от функции 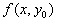 при
при 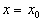 ,
,
т. е.
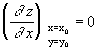 .
.
Аналогично функция 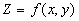 при постоянном
при постоянном 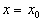 , как функция одного
, как функция одного 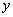 , достигает экстремума при
, достигает экстремума при 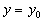 . Значит,
. Значит,
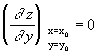
Что и требовалось доказать.
Точка 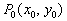 , координаты которой обращают в нуль обе частные производные функции
, координаты которой обращают в нуль обе частные производные функции 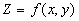 , называется стационарной точкой функции
, называется стационарной точкой функции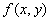 .
.
Уравнение касательной плоскости к поверхности 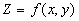 :
:
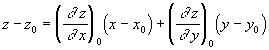
для стационарной точки 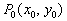 принимает вид
принимает вид 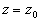 .
.
Следовательно, необходимое условие достижения дифференцируемой функцией 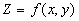 экстремума в точке
экстремума в точке 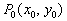 геометрически выражается в том, что касательная плоскость к поверхности - графику функции в соответствующей ее точке параллельна плоскости независимых переменных.
геометрически выражается в том, что касательная плоскость к поверхности - графику функции в соответствующей ее точке параллельна плоскости независимых переменных.
Для отыскания стационарных точек функции 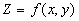 нужно приравнять нулю обе ее частные производные
нужно приравнять нулю обе ее частные производные
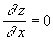 ,
, 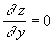 . (*)
. (*)
и решить полученную систему двух уравнений с двумя неизвестными.
Пример 1: Найдем стационарные точки функции
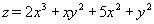
Система уравнений (*) имеет вид:
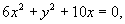
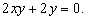
Из второго уравнения следует, что или 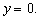 , или
, или 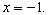 .
.
Подставляя по очереди эти значения в первое уравнение, найдем четыре стационарные точки:
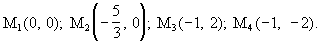
Какие из найденных точек действительно являются точками экстремума, мы установим после приведения достаточного условия экстремума.
Иногда удается, и, не прибегая к достаточным условиям, выяснить характер стационарной точки функции. Так, если из условия задачи непосредственно следует, что рассматриваемая функция имеет где- то максимум или минимум и пи этом системе уравнений (*) удовлетворяет только одна точка (т. е. Одна пара значений x и y), то ясно, что эта пара и будет искомой точкой экстремума функции.
Заметим, наконец, что точками экстремума непрерывной функции двух переменных могут быть точки, в которых функция недифференцируема (им соответствуют острия поверхности - графика функции).
Так, например, функция 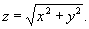 имеет, очевидно, в начале координат минимум, равный нулю, но в этой точке функция недифференцируема; график этой функции есть круглый конус с вершиной в начале координат и осью, совпадающей с осью
имеет, очевидно, в начале координат минимум, равный нулю, но в этой точке функция недифференцируема; график этой функции есть круглый конус с вершиной в начале координат и осью, совпадающей с осью 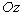 .
.
Следовательно, если иметь в виду не только дифференцируемые, но и вообще непрерывные функции, то нужно сказать, что точками экстремума могут быть стационарные точки и точки, в которых функция недифференцируема.
Вполне аналогично определяется понятие экстремума функции любого числа независимых переменных.
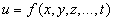
и устанавливаются необходимые условия экстремума. Именно: Дифференцируемая функция n переменных может иметь экстремумы только при тех значениях x, y, z,..., t, при которых равны нулю все ее n частных производных первого порядка:


Эти равенства образуют систему n уравнений с n неизвестными.
Теперь определим достаточные условия для экстремума функции двух переменных. Так же как и для функции одной переменной, необходимый признак экстремума в случае многих переменных не является достаточным. Это значит, что из равенства нулю частных производных в данной точке вовсе не следует, что эта точка обязательно является точкой экстремума. Возьмем функцию 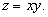 Ее частные производные
Ее частные производные 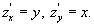 равны нулю в начале координат,
равны нулю в начале координат,
однако функция экстремума не достигает. В самом деле, функция 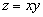 , будучи равной нулю в начале координат, имеет в любой близости к началу координат как положительные значения (в первом и третьем координатных углах), так и отрицательные (во втором и четвертом координатных углах), и значит, нуль не является ни наибольшим, ни наименьшим значением этой функции.
, будучи равной нулю в начале координат, имеет в любой близости к началу координат как положительные значения (в первом и третьем координатных углах), так и отрицательные (во втором и четвертом координатных углах), и значит, нуль не является ни наибольшим, ни наименьшим значением этой функции.
Достаточные условия экстремума для функции нескольких переменных носят значительно более сложный характер, чем для функции одной переменной. Мы рассмотрим эти условия без доказательства только для функции двух переменных.
Пусть точка 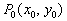 является стационарной точкой функции
является стационарной точкой функции 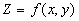 , т. е.
, т. е. 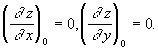
Вычислим в точке 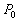 значение вторых частных производных функции
значение вторых частных производных функции 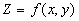 и обозначим их для краткости буквами A, B и C:
и обозначим их для краткости буквами A, B и C:
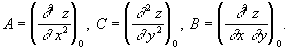
Если 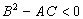 , то функция
, то функция 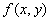 имеет в точке
имеет в точке 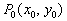 экстремум: при A<0 и C<0 и минимум при A>0 и C>0 (Из условия
экстремум: при A<0 и C<0 и минимум при A>0 и C>0 (Из условия 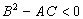 следует, что A и C обязательно имеют одинаковые знаки).
следует, что A и C обязательно имеют одинаковые знаки).
Если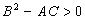 , то точка
, то точка 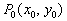 не является точкой экстремума.
не является точкой экстремума.
Если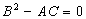 , то неясно, является ли точка
, то неясно, является ли точка 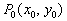 точкой экстремума и требуется дополнительное исследование.
точкой экстремума и требуется дополнительное исследование.
Пример:
1) Ранее в примере было установлено, что функция
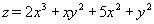
имеет четыре стационарные точки:
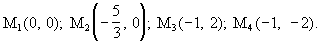
Вторые частные производные данной функции равны
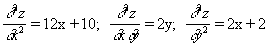
В точке 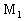 имеем: A=10, B=0, C=2. Здесь
имеем: A=10, B=0, C=2. Здесь 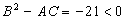 ; значит, точка
; значит, точка 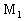 является точкой экстремума, и так как A и C положительны, то этот экстремум - минимум.
является точкой экстремума, и так как A и C положительны, то этот экстремум - минимум.
В точке 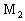 соответственно будет A=-10, B=0, C=-4/3; .
соответственно будет A=-10, B=0, C=-4/3; .
Это точка максимума. Точки 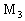 и
и 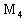 не являются экстремумами функции (т.к. в них
не являются экстремумами функции (т.к. в них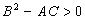 ).
).
2) Найдем точки экстремума функции 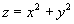 ;
;
Приравнивая частные производные нулю:
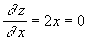 ,
, 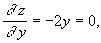
находим одну стационарную точку - начало координат. Здесь A=2, B=0, C= -2. Cледовательно, 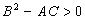 и точка (0, 0)
и точка (0, 0)
не является точкой экстремума. Уравнение 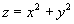 есть уравнение гиперболического параболоида (см. Рис. 2.) по рисунку видно, что точка (0, 0) не является точкой экстремума.
есть уравнение гиперболического параболоида (см. Рис. 2.) по рисунку видно, что точка (0, 0) не является точкой экстремума.
Локальные Экстремумы
Определение1: Говорят, что функция 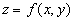 имеет в точке
имеет в точке 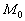 локальный максимум, если существует такая окрестность точки
локальный максимум, если существует такая окрестность точки 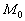 , для которой для всякой точки M с координатами (x, y) выполняется неравенство:
, для которой для всякой точки M с координатами (x, y) выполняется неравенство: 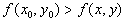 . При этом,
. При этом, 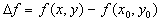 т. е. приращение функции < 0.
т. е. приращение функции < 0.
Определение2: Говорят, что функция 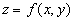 имеет в точке
имеет в точке 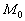 локальный минимум, если существует такая окрестность точки
локальный минимум, если существует такая окрестность точки 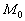 , для которой для всякой точки M с координатами (x, y) выполняется неравенство:
, для которой для всякой точки M с координатами (x, y) выполняется неравенство: 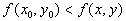 . При этом,
. При этом, 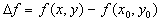 т. е. приращение функции > 0.
т. е. приращение функции > 0.
Определение 3: Точки локальных минимума и максимума называются точками экстремума.
Условные Экстремумы
При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных.
Пусть заданы функция 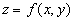 и линия L на плоскости 0xy. Задача состоит в том, чтобы на линии L найти такую точку P(x, y), в которой значение функции
и линия L на плоскости 0xy. Задача состоит в том, чтобы на линии L найти такую точку P(x, y), в которой значение функции 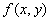 является наибольшим или наименьшим по сравнению со значениями этой функции в точках линии L, находящихся вблизи точки P. Такие точки P называются точками условного экстремума функции
является наибольшим или наименьшим по сравнению со значениями этой функции в точках линии L, находящихся вблизи точки P. Такие точки P называются точками условного экстремума функции 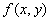 на линии L. В отличие от обычной точки экстремума значение функции в точке условного экстремума сравнивается со значениями функции не во всех точках некоторой ее окрестности, а только в тех, которые лежат на линии L.
на линии L. В отличие от обычной точки экстремума значение функции в точке условного экстремума сравнивается со значениями функции не во всех точках некоторой ее окрестности, а только в тех, которые лежат на линии L.
Совершенно ясно, что точка обычного экстремума (говорят также безусловного экстремума) является и точкой условного экстремума для любой линии, проходящей через эту точку. Обратное же, разумеется, неверно: точка условного экстремума может и не быть точкой обычного экстремума. Поясню сказанное обычным примером. Графиком функции
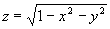 является верхняя полусфера (Рис 3).
является верхняя полусфера (Рис 3).
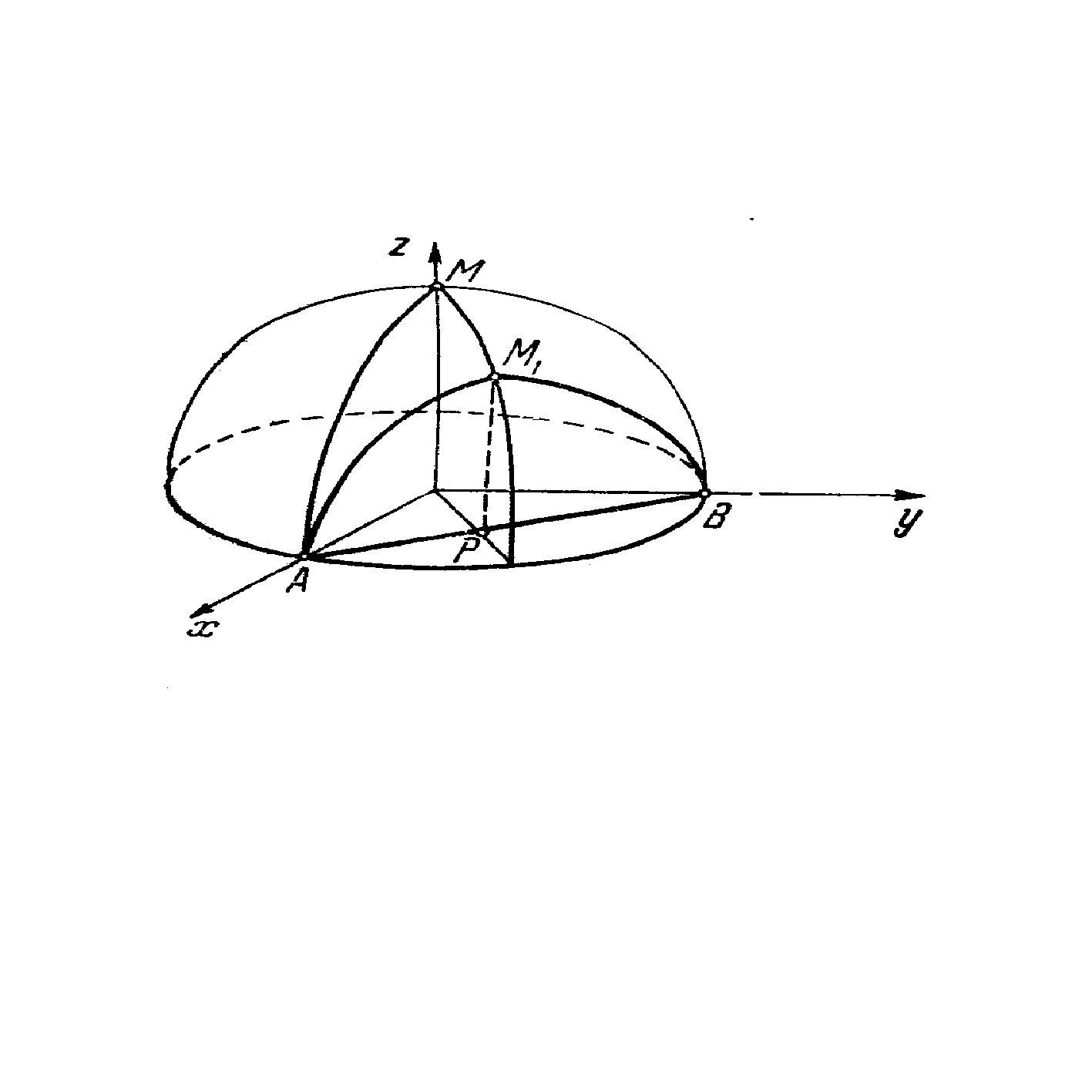
Эта функция имеет максимум в начале координат; ему соответствует вершина M полусферы. Если линия L есть прямая, проходящая через точки А и В (ее уравнение x+y-1=0), то геометрически ясно, что для точек этой линии наибольшее значение функции достигается в точке 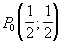 , лежащей посередине между точками А и В. Это и есть точка условного экстремума (максимума) функции
, лежащей посередине между точками А и В. Это и есть точка условного экстремума (максимума) функции 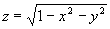 на данной линии; ей соответствует точка M1 на полусфере, и из рисунка видно, что ни о каком обычном экстремуме здесь не может быть речи.
на данной линии; ей соответствует точка M1 на полусфере, и из рисунка видно, что ни о каком обычном экстремуме здесь не может быть речи.
Отметим, что в заключительной части задачи об отыскании наибольшего и наименьшего значений функции в замкнутой области нам приходится находить экстремальные значения функции на границе этой области, т.е. на какой-то линии, и тем самым решать задачу на условный экстремум.
Приступим теперь к практическому отысканию точек условного экстремума функции Z= f(x, y) при условии, что переменные x и y связаны уравнением j (x, y) = 0. Это соотношение будем называть уравнение связи. Если из уравнения связи y можно выразить явно через х: y=j (x), мы получим функцию одной переменной Z= f(x, j (x)) = Ф(х).
Найдя значение х, при которых эта функция достигает экстремума, и определив затем из уравнения связи соответствующие им значения у, мы и получим искомые точки условного экстремума.
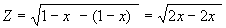 Так, в вышеприведенном примере из уравнения связи x+y-1=0 имеем y=1-х. Отсюда
Так, в вышеприведенном примере из уравнения связи x+y-1=0 имеем y=1-х. Отсюда
Легко проверить, что z достигает максимума при х = 0,5; но тогда из уравнения связи y=0,5, и мы получаем как раз точку P, найденную из геометрических соображений.
Очень просто решается задача на условный экстремум и тогда, когда уравнение связи можно представить параметрическими уравнениями х=х(t), y=y(t). Подставляя выражения для х и у в данную функцию, снова приходим к задаче отыскания экстремума функции одной переменной.
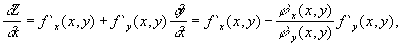 Если уравнение связи имеет более сложный вид и нам не удается ни явно выразить одну переменную через другую, ни заменить его параметрическими уравнениями, то задача отыскания условного экстремума становится более трудной. Будем по-прежнему считать, что в выражении функции z= f(x, y) переменная j
(x, y) = 0. Полная производная от функции z= f(x, y) равна:
Если уравнение связи имеет более сложный вид и нам не удается ни явно выразить одну переменную через другую, ни заменить его параметрическими уравнениями, то задача отыскания условного экстремума становится более трудной. Будем по-прежнему считать, что в выражении функции z= f(x, y) переменная j
(x, y) = 0. Полная производная от функции z= f(x, y) равна:
Где производная y`, найдена по правилу дифференцирования неявной функции. В точках условного экстремума найденная полная производная должна ровняться нулю; это дает одно уравнение, связывающее х и у. Так как они должны удовлетворять еще и уравнению связи, то мы получаем систему двух уравнений с двумя неизвестными
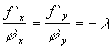
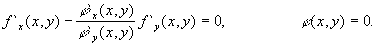 Преобразуем эту систему к гораздо более удобной, записав первое уравнение в виде пропорции и введя новую вспомогательную неизвестную l
:
Преобразуем эту систему к гораздо более удобной, записав первое уравнение в виде пропорции и введя новую вспомогательную неизвестную l
:
(знак минус перед l поставлен для удобства). От этих равенств легко перейти к следующей системе:
f`x=(x,y)+l j `x(x,y)=0, f`y(x,y)+l j `y(x,y)=0 (*),
которая вместе с уравнением связи j (x, y) = 0 образует систему трех уравнений с неизвестными х, у и l .
Эти уравнения (*) легче всего запомнить при помощи следующего правила: для того, чтобы найти точки, которые могут быть точками условного экстремума функции
Z= f(x, y) при уравнении связи j (x, y) = 0, нужно образовать вспомогательную функцию
Ф(х,у)=f(x,y)+l j (x,y)
Где l -некоторая постоянная, и составить уравнения для отыскания точек экстремума этой функции.
Указаная система уравнений доставляет, как правило, только необходимые условия, т.е. не всякая пара значений х и у, удовлетворяющая этой системе, обязательно является точкой условного экстремума. Достаточные условия для точек условного экстремума я приводить не стану; очень часто конкретное содержание задачи само подсказывает, чем является найденная точка. Описанный прием решения задач на условный экстремум называется методом множителей Лагранжа.
Метод множителей Лагранжа имеет наглядный геометрический смысл, который я сейчас поясню.
Предположим, что на рис 4. Изображены линии уровня функции Z= f(x, y) и линия L, на которой отыскиваются точки условного экстремума.
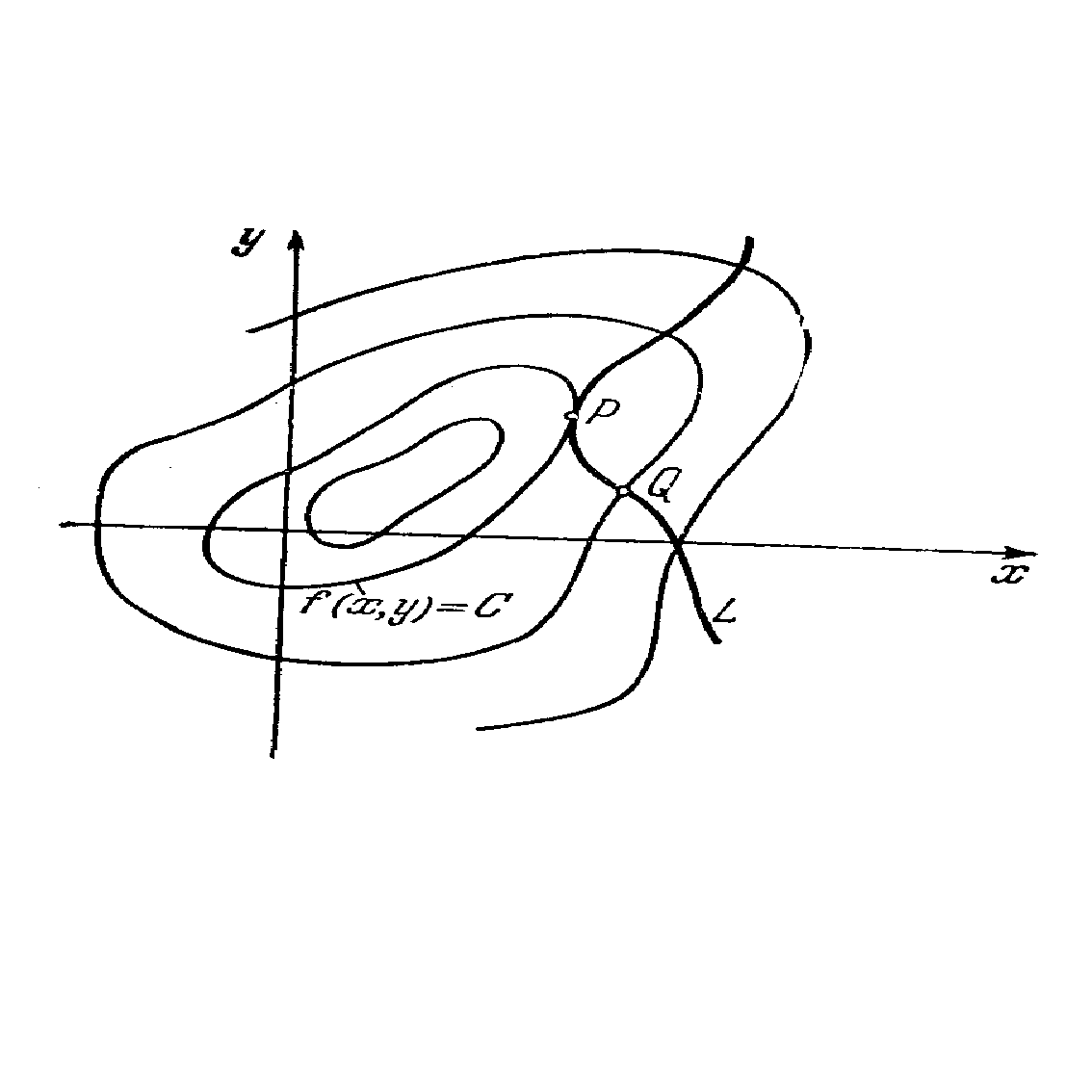
Если в точке Q линия L пересекает линию уровня, то эта точка не может быть точкой условного экстремума т.к. по одну сторону от линии уровня функция Z= f(x, y) принимает большие значения, а по другую - меньшие. Если же в точке P линия L не пересекает соответствующую линию уровня и, значит, в некоторой окрестности этой точки лежит по одну сторону от линии уровня, то точка P будет как раз являться точкой
условного экстремума. В такой точке линия L и линия уровня Z= f(x, y) =С касаются друг друга (предполагается, что линии гладкие). И угловые коэффициенты касательных к ним должны быть равны. Из уравнения связи j (x, y) = 0 имеем
y`=-j `x/j `y, а из уравнения линии уровня y`=-fx`/fy`. Приравнивая производные и произведя простейшее преобразование мы получим уравнение
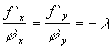 Приведенное рассуждение теряет силу, если линия уровня такова, что во всех ее точках fx`=0, fy`=0. Можно рассмотреть, например, функцию z = 4-x2 и линию уровня x=0, соответствующую значению z = 4.
Приведенное рассуждение теряет силу, если линия уровня такова, что во всех ее точках fx`=0, fy`=0. Можно рассмотреть, например, функцию z = 4-x2 и линию уровня x=0, соответствующую значению z = 4.
Можно искать условный экстремум функции f(x,y,z) при двух уравнениях связи: j 1(x, y, z) = 0 и j 2(x, y, z) = 0
Эти уравнения определяют линию в пространстве. Таким образом задача сводится к отысканию такой точки линии, в которой функция принимает экстремальное значение, причем сравниваются значения функции только в точках рассматриваемой линии.
Метод множителей Лагранжа в этом случае принимается следующим образом: строим вспомогательную функцию
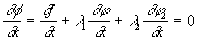
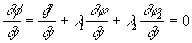 Ф(x, y, z) = f(x, y, z)+l
1j
1(x, y, z) +l
2j
2(x, y, z), где l
1 и l
2- новые дополнительные неизвестные, и состовляем систему уравнений для отыскания экстремумов этой функции.
Ф(x, y, z) = f(x, y, z)+l
1j
1(x, y, z) +l
2j
2(x, y, z), где l
1 и l
2- новые дополнительные неизвестные, и состовляем систему уравнений для отыскания экстремумов этой функции.
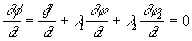 Добавляя сюда два уравнения связи получаем систему уравнений с пятью неизвестными x, y, z, l
1, l
2. Искомыми точками условного экстремума могут быть только те, координаты х, у, z которых являются решением этой системы.
Добавляя сюда два уравнения связи получаем систему уравнений с пятью неизвестными x, y, z, l
1, l
2. Искомыми точками условного экстремума могут быть только те, координаты х, у, z которых являются решением этой системы.
Список использованной литературы:
А.Ф. Бермант, И.Г. Абрамович. Краткий курс математического анализа.
Шипачев Учебник высшей математики