–†–µ—Д–µ—А–∞—В: –Э–∞—Е–Њ–ґ–і–µ–љ–Є–µ –Њ–њ—В–Є–Љ–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –і–ї—П –њ–Њ–ї–µ—В–∞ —В–µ–ї–∞ —З–µ—А–µ–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Г—О –њ—А–µ–≥—А–∞–і—Г
–Т—Л–њ–Њ–ї–љ–Є–ї: —Г—З–µ–љ–Є–Ї 11 –С –Ї–ї–∞—Б—Б–∞ –Э–∞–Ј–∞—А–Ї–Є–љ –Я–∞–≤–µ–ї –Ф–Љ–Є—В—А–Є–µ–≤–Є—З
–Ь—Г–љ–Є—Ж–Є–њ–∞–ї—М–љ–Њ–µ –Њ–±—Й–µ–Њ–±—А–∞–Ј–Њ–≤–∞—В–µ–ї—М–љ–Њ–µ —Г—З—А–µ–ґ–і–µ–љ–Є–µ¬† ¬Ђ–Ы–Є—Ж–µ–є вДЦ43¬ї
–°–∞—А–∞–љ—Б–Ї, 2004
–Я–Њ—Б—В–∞–љ–Њ–≤–Ї–∞ –Ј–∞–і–∞—З–Є.
–Я—А–Њ–Є–Ј–≤–µ—Б—В–Є –љ–µ–Њ–±—Е–Њ–і–Є–Љ—Л–µ —А–∞—Б—З–µ—В—Л –і–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Љ–Є–љ–Є–Љ–∞–ї—М–љ–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є —В–µ–ї–∞, –±—А–Њ—И–µ–љ–љ–Њ–≥–Њ —З–µ—А–µ–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–µ –њ—А–µ–њ—П—В—Б—В–≤–Є–µ.
–Ь–µ—В–Њ–і—Л –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П —А–∞–±–Њ—В—Л.
–Ф–ї—П –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П –і–∞–љ–љ–Њ–є —А–∞–±–Њ—В—Л –њ—А–Њ–і–µ–ї–∞–µ–Љ —А—П–і –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—Е –≤—Л—З–Є—Б–ї–µ–љ–Є–є –Є –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ —Д–Є–Ј–Є—З–µ—Б–Ї–Є—Е —Д–Њ—А–Љ—Г–ї.
–Ч–љ–∞—П,
—З—В–Њ —В—А–∞–µ–Ї—В–Њ—А–Є–µ–є –і–≤–Є–ґ–µ–љ–Є—П —В–µ–ї–∞, —П–≤–ї—П–µ—В—Б—П –њ–∞—А–∞–±–Њ–ї–∞, –∞ —В–∞–Ї–ґ–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї—Г—О
—Д–Њ—А–Љ—Г–ї—Г –Ј–∞–њ–Є—Б–Є –і–∞–љ–љ–Њ–є –ї–Є–љ–Є–Є, –±—Г–і–µ–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ –њ–∞—А–∞–±–Њ–ї—Л –Њ–±—Й–µ–≥–Њ –≤–Є–і–∞
–≤ –Ї–∞—З–µ—Б—В–≤–µ –љ–∞—З–∞–ї—М–љ—Л—Е –і–∞–љ–љ—Л—Е –њ–Њ—Б—В–∞–≤–ї–µ–љ–љ–Њ–є –Ј–∞–і–∞—З–Є. –Т –≤—Л–±—А–∞–љ–љ–Њ–є –љ–∞–Љ–Є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–є
—Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В –Ј–∞–њ–Є—И–µ–Љ –і–∞–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П –і–≤—Г—Е —В–Њ—З–µ–Ї, –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—Й–Є—Е –ї–Є–љ–Є–Є
–і–≤–Є–ґ–µ–љ–Є—П вАУ –љ–∞—З–∞–ї—М–љ–Њ–є —В–Њ—З–Ї–µ –Р –Є —В–Њ—З–Ї–µ –Т, –≤ –Ї–Њ—В–Њ—А–Њ–є —В–µ–ї–Њ –Њ–Ї–∞–ґ–µ—В—Б—П —З–µ—А–µ–Ј –љ–µ–Ї–Њ—В–Њ—А—Л–є
–њ—А–Њ–Љ–µ–ґ—Г—В–Њ–Ї –≤—А–µ–Љ–µ–љ–Є t. –†–µ—И–∞—П —Б–Є—Б—В–µ–Љ—Г –њ–Њ–ї—Г—З–µ–љ–љ—Л—Е –њ—А–Є —Н—В–Њ–Љ —Г—А–∞–≤–љ–µ–љ–Є–є, –њ—Г—В–µ–Љ
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—Е –Ј–∞–Љ–µ–љ –Є –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є –≤—Л–≤–µ–і–µ–Љ —Д–Њ—А–Љ—Г–ї—Г –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –і–≤–Є–ґ–µ–љ–Є—П —В–µ–ї–∞
–Њ—В –Њ–і–љ–Њ–є –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є L, —В.–µ. –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л k –Є b, —Г—З–∞—Б—В–≤—Г—О—Й–Є–µ –≤ –Њ–±—Й–µ–Љ –≤–Є–і–µ
—Г—А–∞–≤–љ–µ–љ–Є—П –њ–∞—А–∞–±–Њ–ї—Л, –≤—Л—А–∞–Ј–Є–Љ —З–µ—А–µ–Ј L. –Ч–∞—В–µ–Љ, –Є—Б–њ–Њ–ї—М–Ј—Г—П —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є –Ј–∞–Ї–Њ–љ –і–≤–Є–ґ–µ–љ–Є—П
—В–µ–ї–∞, –±—А–Њ—И–µ–љ–љ–Њ–≥–Њ –њ–Њ–і —Г–≥–ї–Њ–Љ –Ї –≥–Њ—А–Є–Ј–Њ–љ—В—Г, –≤—Л—А–∞–Ј–Є–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Г—О L —З–µ—А–µ–Ј ![]() ¬†–Є V . –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –њ–Њ–ї—Г—З–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–≤–Є–ґ–µ–љ–Є—П,
–≤ –Ї–∞—З–µ—Б—В–≤–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –≤ –Ї–Њ—В–Њ—А–Њ–Љ –±—Г–і—Г—В –≤—Л—Б—В—Г–њ–∞—В—М –њ–µ—А–µ–Љ–µ–љ–љ—Л–µ
¬†–Є V . –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –њ–Њ–ї—Г—З–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–≤–Є–ґ–µ–љ–Є—П,
–≤ –Ї–∞—З–µ—Б—В–≤–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –≤ –Ї–Њ—В–Њ—А–Њ–Љ –±—Г–і—Г—В –≤—Л—Б—В—Г–њ–∞—В—М –њ–µ—А–µ–Љ–µ–љ–љ—Л–µ ![]() ¬†–Є V. –Ч–∞—В–µ–Љ —Б–Њ—Б—В–∞–≤–Є–Љ —Б–Є—Б—В–µ–Љ—Г –і–≤—Г—Е —Г—А–∞–≤–љ–µ–љ–Є–є,
–њ–Њ–ї—Г—З–µ–љ–љ—Л—Е –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В —В–Њ—З–µ–Ї –Р –Є –Т –≤ –њ–Њ—Б–ї–µ–і–љ–µ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–≤–Є–ґ–µ–љ–Є—П.
–†–µ—И–∞—П –і–∞–љ–љ—Г—О —Б–Є—Б—В–µ–Љ—Г, –Љ—Л –љ–∞–є–і–µ–Љ –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л–µ –љ–∞–Љ –≤–µ–ї–Є—З–Є–љ—Л
¬†–Є V. –Ч–∞—В–µ–Љ —Б–Њ—Б—В–∞–≤–Є–Љ —Б–Є—Б—В–µ–Љ—Г –і–≤—Г—Е —Г—А–∞–≤–љ–µ–љ–Є–є,
–њ–Њ–ї—Г—З–µ–љ–љ—Л—Е –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В —В–Њ—З–µ–Ї –Р –Є –Т –≤ –њ–Њ—Б–ї–µ–і–љ–µ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–≤–Є–ґ–µ–љ–Є—П.
–†–µ—И–∞—П –і–∞–љ–љ—Г—О —Б–Є—Б—В–µ–Љ—Г, –Љ—Л –љ–∞–є–і–µ–Љ –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л–µ –љ–∞–Љ –≤–µ–ї–Є—З–Є–љ—Л ![]() ¬†–Є V, –≤—Л—А–∞–Ј–Є–≤ –Є—Е —З–µ—А–µ–Ј –Є–Љ–µ—О—Й–Є–µ—Б—П –Є–Ј–≤–µ—Б—В–љ—Л–µ –љ–∞–Љ
–њ–∞—А–∞–Љ–µ—В—А—Л вАУ —И–Є—А–Є–љ—Г –Є –≤—Л—Б–Њ—В—Г –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ –њ—А–µ–њ—П—В—Б—В–≤–Є—П. –Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П Vmin
–≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є.
¬†–Є V, –≤—Л—А–∞–Ј–Є–≤ –Є—Е —З–µ—А–µ–Ј –Є–Љ–µ—О—Й–Є–µ—Б—П –Є–Ј–≤–µ—Б—В–љ—Л–µ –љ–∞–Љ
–њ–∞—А–∞–Љ–µ—В—А—Л вАУ —И–Є—А–Є–љ—Г –Є –≤—Л—Б–Њ—В—Г –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ –њ—А–µ–њ—П—В—Б—В–≤–Є—П. –Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П Vmin
–≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є.
–†–µ—И–µ–љ–Є–µ.
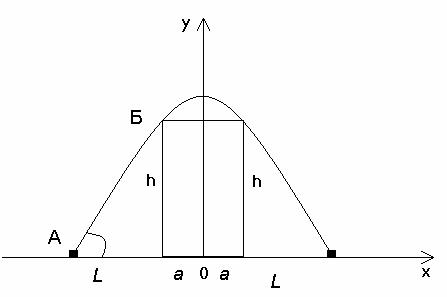
–£—А–∞–≤–љ–µ–љ–Є–µ–Љ –ї–Є–љ–Є–Є –і–≤–Є–ґ–µ–љ–Є—П —В–µ–ї–∞, –±—А–Њ—И–µ–љ–љ–Њ–≥–Њ —З–µ—А–µ–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–µ –њ—А–µ–њ—П—В—Б—В–≤–Є–µ, –≤ –Њ–±—Й–µ–Љ –≤–Є–і–µ —П–≤–ї—П–µ—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є–µ –њ–∞—А–∞–±–Њ–ї—Л :
y=-kx2+b
–Т–≤–µ–і–µ–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Г—О —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В –Є —Б–≤—П–ґ–µ–Љ –µ–µ —Б –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–Љ –њ—А–µ–њ—П—В—Б—В–≤–Є–µ–Љ, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Т –і–∞–љ–љ–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В —Г—А–∞–≤–љ–µ–љ–Є–µ –і–≤–Є–ґ–µ–љ–Є—П —В–µ–ї–∞ –≤ —В–Њ—З–Ї–∞—Е –Р –Є –С –њ—А–Є–Љ–µ—В –≤–Є–і:
![]()  0=-k(a+L)2+b,
 0=-k(a+L)2+b,
h=-ka2+b.
–Т—Л—А–∞–Ј–Є–Љ k –Є b —З–µ—А–µ–Ј –Њ–і–љ—Г –љ–µ–Є–Ј–≤–µ—Б—В–љ—Г—О L:
–Т—Л—З–Є—В–∞–µ–Љ 1)-–Њ–µ –Є–Ј 2)-–Њ–≥–Њ:
h=k(a2+2aL+L2-a2),
h=k(2aL+L2) ,![]() (*);
(*);
![]()
![]() h=b-ka2+b b=h+ka2
h=b-ka2+b b=h+ka2 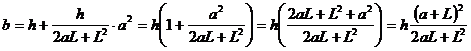 . (*)
. (*)
–Я–Њ–ї—Г—З–Є–ї–Њ—Б—М, —З—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–≤–Є–ґ–µ–љ–Є—П –Ј–∞–≤–Є—Б–Є—В —В–Њ–ї—М–Ї–Њ –Њ—В L:
y=-kx2+b, –≥–і–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л k –Є b –Є–Љ–µ—О—В –≤–Є–і (*).
–Э–∞–є–і–µ–Љ
–Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М L –Њ—В![]() –Є V.
–Є V.
–Ш–Ј –Ї—Г—А—Б–∞ —Д–Є–Ј–Є–Ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ: —З—В–Њ –і–≤–Є–ґ–µ–љ–Є–µ —В–µ–ї–∞, –±—А–Њ—И–µ–љ–љ–Њ–≥–Њ –њ–Њ–і —Г–≥–ї–Њ–Љ –≥–Њ—А–Є–Ј–Њ–љ—В–∞ –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є—П–Љ–Є
![]()
![]()
![]()  x=Vxt L=Vxt L=Vcos
 x=Vxt L=Vxt L=Vcos![]() t
t
![]()
![]()  y=Vyt+gt2/2 h=Vyt-gy t2/2 gt2-2Vyt+2h=0.
 y=Vyt+gt2/2 h=Vyt-gy t2/2 gt2-2Vyt+2h=0.
gt2-2Vyt+2h=0.
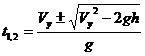 .
.
–Ь—Л —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ –≤—А–µ–Љ—П –і–≤–Є–ґ–µ–љ–Є—П –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ –С, –Ј–љ–∞—З–Є—В
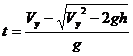 , –≥–і–µ Vy=Vsin
, –≥–і–µ Vy=Vsin![]() .
.
–Ш—В–∞–Ї,
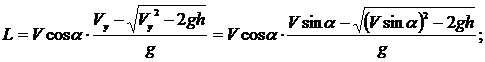 ¬†
 
–£–Љ–љ–Њ–ґ–Є–≤ –Њ–±–µ —З–∞—Б—В–Є —Г—А–∞–≤–љ–µ–љ–Є—П –љ–∞ g, –њ–Њ–ї—Г—З–Є–Љ:
![]()  (1)
 (1)
–Ш–Ј–≤–µ—Б—В–љ–Њ,
—З—В–Њ 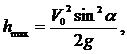 ¬†—В.–µ.
¬†—В.–µ. ![]()
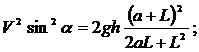 ¬†(2)
 (2)
–°
–і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л tg![]() =yвАЩ –≤ —В–Њ—З–Ї–µ –Р,
—В.–µ. tg
=yвАЩ –≤ —В–Њ—З–Ї–µ –Р,
—В.–µ. tg![]() =yвАЩ(-a-L);
=yвАЩ(-a-L);
![]()
–Я–Њ–і—Б—В–∞–≤–Є–≤
–Ј–љ–∞—З–µ–љ–Є–µ tg![]() –≤ (2),
–њ–Њ–ї—Г—З–Є–Љ:
–≤ (2),
–њ–Њ–ї—Г—З–Є–Љ:
V2sin2![]() =g(a+L) tg
=g(a+L) tg ![]()
![]()
![]() V2sin
V2sin![]() cos
cos![]() =g(a+L)
Lg=V2sin
=g(a+L)
Lg=V2sin![]() cos
cos![]() -ga (3)
-ga (3)
–°—А–∞–≤–љ–Є–≤ (1) –Є (3) –њ–Њ–ї—Г—З–∞–µ–Љ, —З—В–Њ:
![]()
![]() .
.
–Я–Њ–ї—Г—З–Є–ї–Є
—Г—А–∞–≤–љ–µ–љ–Є–µ —Б –і–≤—Г–Љ—П –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л–Љ–Є V –Є![]() : –≤—Л—А–∞–Ј–Є–≤ V —З–µ—А–µ–Ј
: –≤—Л—А–∞–Ј–Є–≤ V —З–µ—А–µ–Ј
![]() , –Љ—Л –њ–Њ–ї—Г—З–Є–Љ
—В—Г —Б–∞–Љ—Г—О —Д—Г–љ–Ї—Ж–Є—О, –Ї–Њ—В–Њ—А—Г—О –Љ—Л –і–Њ–ї–ґ–љ—Л –±—Л–ї–Є –љ–∞–є—В–Є:
, –Љ—Л –њ–Њ–ї—Г—З–Є–Љ
—В—Г —Б–∞–Љ—Г—О —Д—Г–љ–Ї—Ж–Є—О, –Ї–Њ—В–Њ—А—Г—О –Љ—Л –і–Њ–ї–ґ–љ—Л –±—Л–ї–Є –љ–∞–є—В–Є:
–Я—Г—Б—В—М
z=V2, —В–Њ–≥–і–∞ z cos2![]() (z sin2
(z sin2![]() -2gh)=g2a2;
-2gh)=g2a2;
z2 cos2![]() sin2
sin2![]() - z cos2
- z cos2![]() 2gh-g2a2=0;
2gh-g2a2=0;
–Я–Њ–ї—Г—З–Є–ї–Є –Ї–≤–∞–і—А–∞—В–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ z
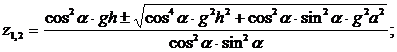
–Ю—З–µ–≤–Є–і–љ–Њ,
![]() ¬†–Ј–љ–∞—З–Є—В, —В.–Ї. z=V2>0, —В–Њ
¬†–Ј–љ–∞—З–Є—В, —В.–Ї. z=V2>0, —В–Њ 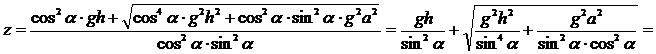
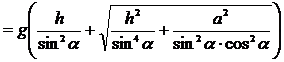 .
.
–Т–Љ–µ—Б—В–Њ
–Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є V –Њ—В ![]() —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ
–Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М z –Њ—В
—А–∞—Б—Б–Љ–Њ—В—А–Є–Љ
–Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М z –Њ—В ![]() , –Є –Њ–±–Њ–Ј–љ–∞—З–Є–≤
, –Є –Њ–±–Њ–Ј–љ–∞—З–Є–≤ ![]() ¬†–њ–Њ–ї—Г—З–Є–Љ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М z –Њ—В t.
¬†–њ–Њ–ї—Г—З–Є–Љ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М z –Њ—В t.
–Я–Њ–ї—Г—З–Є–Љ
![]() , –≥–і–µ z=V2,
, –≥–і–µ z=V2, ![]() .
.
–Т—Л—А–∞–Ј–Є–Љ
![]() ¬†—З–µ—А–µ–Ј t, –µ—Б–ї–Є
¬†—З–µ—А–µ–Ј t, –µ—Б–ї–Є ![]() ;
; ![]()  
 ![]()
–Ч–љ–∞—З–Є—В,
![]()
–Ґ.–µ.
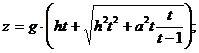 ¬†
 
![]()
–Ґ–∞–Ї–Є–Љ
–Њ–±—А–∞–Ј–Њ–Љ, —З—В–Њ–±—Л –љ–∞–є—В–Є Vmin –Є ![]() , –љ–∞–Љ –љ—Г–ґ–љ–Њ
–≤–Њ-–њ–µ—А–≤—Л—Е, –љ–∞–є—В–Є fmin –Є t.
, –љ–∞–Љ –љ—Г–ґ–љ–Њ
–≤–Њ-–њ–µ—А–≤—Л—Е, –љ–∞–є—В–Є fmin –Є t.
![]()  
¬†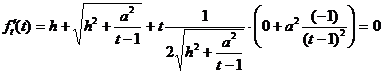 .
.
–£–Љ–љ–Њ–ґ–Є–≤
–Њ–±–µ —З–∞—Б—В–Є —Г—А–∞–≤–љ–µ–љ–Є—П –љ–∞ ![]() , –њ–Њ–ї—Г—З–Є–Љ
, –њ–Њ–ї—Г—З–Є–Љ
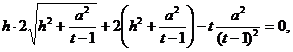
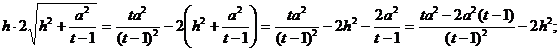
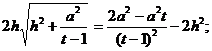
–Я—А–µ–ґ–і–µ
—З–µ–Љ –≤–Њ–Ј–≤–µ—Б—В–Є –Њ–±–µ —З–∞—Б—В–Є –≤ –Ї–≤–∞–і—А–∞—В, —Б–і–µ–ї–∞–µ–Љ –њ—А–µ–і–≤–∞—А–Є—В–µ–ї—М–љ—Л–є –∞–љ–∞–ї–Є–Ј –њ–Њ–ї—Г—З–Є–≤—И–µ–≥–Њ—Б—П
—Г—А–∞–≤–љ–µ–љ–Є—П: —В.–Ї. ![]()
—В–Њ
–Є ![]()
—В.–µ.
![]() ¬†–Є
¬†–Є ![]()
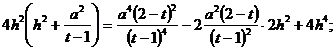
![]()
![]()
![]()
–£–Љ–љ–Њ–ґ–Є–≤ –Њ–±–µ —З–∞—Б—В–Є —Г—А–∞–≤–љ–µ–љ–Є—П –љ–∞ (t-1)2, –њ–Њ–ї—Г—З–Є–Љ
![]()
![]()
![]() ¬†–Ґ.–Ї t<2 –Є t>1 (—В.–Ї.
¬†–Ґ.–Ї t<2 –Є t>1 (—В.–Ї. ![]() ), —В–Њ –Љ–Њ–ґ–љ–Њ
–Є–Ј–≤–ї–µ—З—М –Ї–Њ—А–µ–љ—М.
), —В–Њ –Љ–Њ–ґ–љ–Њ
–Є–Ј–≤–ї–µ—З—М –Ї–Њ—А–µ–љ—М.
![]()  
 ![]()
![]()  
 
![]()  
 ![]()
![]()
![]() ; (4)
; (4)
![]()
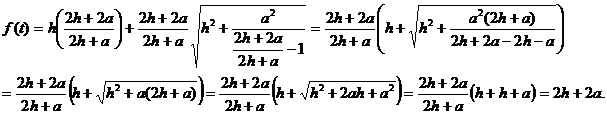
 –Ш—В–∞–Ї,
f(t)=2h+2a, –Ј–љ–∞—З–Є—В
–Ш—В–∞–Ї,
f(t)=2h+2a, –Ј–љ–∞—З–Є—В ![]() .
.
–Ґ.–Ї.
z=V2, —В–Њ ![]() ¬†—В.–µ.
¬†—В.–µ. ![]() ¬†(5)
 (5)
–Ю—Б—В–∞–ї–Њ—Б—М –љ–∞–є—В–Є L:
–Х–≥–Њ –љ–∞–є–і–µ–Љ –Є—Б–њ–Њ–ї—М–Ј—Г—П (3).
![]()
![]()

![]()
![]()

![]()
![]()
–†–µ–Ј—Г–ї—М—В–∞—В—Л —А–∞–±–Њ—В—Л.
–Я—А–Њ–і–µ–ї–∞–љ–љ—Л–Љ —А–∞—Б—З–µ—В–Њ–Љ –Љ—Л –љ–∞—И–ї–Є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М —Б–Ї–Њ—А–Њ—Б—В–Є, –і–≤–Є–ґ–µ–љ–Є—П –±—А–Њ—И–µ–љ–љ–Њ–≥–Њ —З–µ—А–µ–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–µ –њ—А–µ–њ—П—В—Б—В–≤–Є–µ —В–µ–ї–∞, —В–∞–Ї —З—В–Њ–±—Л –Њ–љ–∞ –±—Л–ї–∞ –Љ–Є–љ–Є–Љ–∞–ї—М–љ–Њ–є, –Њ—В –і–ї–Є–љ—Л –Є –≤—Л—Б–Њ—В—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ –њ—А–µ–њ—П—В—Б—В–≤–Є—П. –Ґ–Њ –µ—Б—В—М, –Ј–љ–∞—П –і–∞–љ–љ—Л–µ –њ—А–µ–њ—П—В—Б—В–≤–Є—П, - –µ–≥–Њ –і–ї–Є–љ—Г –Є —И–Є—А–Є–љ—Г вАУ –∞ —В–∞–Ї –ґ–µ —Д–Њ—А–Љ—Г–ї—Л, –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –≤ –і–∞–љ–љ–Њ–є —А–∞–±–Њ—В–µ, –Љ—Л –Љ–Њ–ґ–µ–Љ –Њ–њ—А–µ–і–µ–ї–Є—В—М –љ–∞ –Ї–∞–Ї–Њ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є–Є –Њ—В –њ—А–µ–њ—П—В—Б—В–≤–Є—П, –њ–Њ–і –Ї–∞–Ї–Є–Љ —Г–≥–ї–Њ–Љ –Є —Б –Ї–∞–Ї–Њ–є –Љ–Є–љ–Є–Љ–∞–ї—М–љ–Њ–є —Б–Ї–Њ—А–Њ—Б—В—М—О –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –±—А–Њ—Б–Є—В—М —В–µ–ї–Њ, —З—В–Њ–±—Л –Њ–љ–Њ –њ–µ—А–µ–ї–µ—В–µ–ї–Њ —З–µ—А–µ–Ј —Н—В–Њ –њ—А–µ–њ—П—В—Б—В–≤–Є–µ.
–Р–Ї—В—Г–∞–ї—М–љ–Њ—Б—В—М —В–µ–Љ—Л.
–Ф–∞–љ–љ—Л–µ —А–∞—Б—З–µ—В—Л –Є –≤—Л–≤–µ–і–µ–љ–љ—Л–µ —Д–Њ—А–Љ—Г–ї—Л –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П –≤ —А–∞–Ј–ї–Є—З–љ—Л—Е —Б—Д–µ—А–∞—Е –і–µ—П—В–µ–ї—М–љ–Њ—Б—В–Є —З–µ–ї–Њ–≤–µ–Ї–∞. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, –≤ –≤–Њ–µ–љ–љ–Њ–є –њ—А–∞–Ї—В–Є–Ї–µ, –і–ї—П –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ —А–∞—Б—З–µ—В–∞ –і–≤–Є–ґ–µ–љ–Є—П —В—А–∞–µ–Ї—В–Њ—А–Є–Є —Б–љ–∞—А—П–і–Њ–≤.
–Я—А–Є–ї–Њ–ґ–µ–љ–Є–µ.
–Ъ —А–∞–±–Њ—В–µ –њ—А–Є–ї–∞–≥–∞–µ—В—Б—П –њ—А–Њ–≥—А–∞–Љ–Љ–∞, —А–µ–Ј—Г–ї—М—В–∞—В–Њ–Љ –Ї–Њ—В–Њ—А–Њ–є —П–≤–ї—П–µ—В—Б—П –≤—Л–≤–Њ–і –љ–∞ —Н–Ї—А–∞–љ —В—А–∞–µ–Ї—В–Њ—А–Є–Є –і–≤–Є–ґ–µ–љ–Є—П —В–µ–ї–∞, –±—А–Њ—И–µ–љ–љ–Њ–≥–Њ —З–µ—А–µ–Ј –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–µ –њ—А–µ–њ—П—В—Б—В–≤–Є–µ. –Т—Е–Њ–і–љ—Л–Љ–Є –њ–∞—А–∞–Љ–µ—В—А–∞–Љ–Є –њ—А–Њ–≥—А–∞–Љ–Љ—Л —П–≤–ї—П—О—В—Б—П –і–∞–љ–љ—Л–µ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ –њ—А–µ–њ—П—В—Б—В–≤–Є—П вАУ –µ–≥–Њ –і–ї–Є–љ–∞ –Є –≤—Л—Б–Њ—В–∞. –Я—А–Њ–≥—А–∞–Љ–Љ–∞ –љ–∞–њ–Є—Б–∞–љ–∞ –љ–∞ —П–Ј—Л–Ї–µ –њ—А–Њ–≥—А–∞–Љ–Љ–Є—А–Њ–≤–∞–љ–Є—П Delphi.