–°—В–∞—В—М—П: –Ю—Б–љ–Њ–≤–љ—Л–µ –њ–Њ–ї–Њ–ґ–µ–љ–Є—П –њ—А–Њ—З–љ–Њ—Б—В–љ–Њ–є —В–µ–Њ—А–Є–Є –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П
–Х–ї—М—Ж–Њ–≤ –Ѓ.–Р.
–Ш–ґ–µ–≤—Б–Ї–Є–є –≥–Њ—Б—Г–і–∞—А—Б—В–≤–µ–љ–љ—Л–є —В–µ—Е–љ–Є—З–µ—Б–Ї–Є–є —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В
–°—В–∞—В—М—П –њ–Њ—Б–≤—П—Й–µ–љ–∞ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–Љ—Г –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е –Є –Ї–∞—Б–∞—В–µ–ї—М–љ—Л—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є –≤ –≥—А—Г–љ—В–∞—Е. –Т —Б—В–∞—В—М–µ –і–∞—О—В—Б—П –Њ—Б–љ–Њ–≤–љ—Л–µ –њ—А–µ–і–њ–Њ—Б—Л–ї–Ї–Є —А–∞—Б—З–µ—В–∞. –Т –Є–Ј–≤–µ—Б—В–љ—Л–µ —В–µ–Њ—А–Є–Є –њ—А–Њ—З–љ–Њ—Б—В–Є –≤–љ–Њ—Б—П—В—Б—П –њ–Њ–њ—А–∞–≤–Ї–Є, –Ї–Њ—В–Њ—А—Л–µ —Б —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –∞–≤—В–Њ—А–∞ –і–∞—О—В –±–Њ–ї–µ–µ –Њ–±—К–µ–Ї—В–Є–≤–љ—Л–µ —А–µ–Ј—Г–ї—М—В–∞—В—Л —А–∞—Б—З–µ—В–Њ–≤, –њ–Њ–і—В–≤–µ—А–ґ–і–∞–µ–Љ—Л–µ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ–Є –Ј–∞–Љ–µ—А–∞–Љ–Є.
–Т –Є–Ј–≤–µ—Б—В–љ—Л—Е —В–µ–Њ—А–Є—П—Е –њ—А–Њ—З–љ–Њ—Б—В–Є –Є—Б—Е–Њ–і—П—В –Є–Ј —Б–ї–µ–і—Г—О—Й–Є—Е –Њ—Б–љ–Њ–≤–Њ–њ–Њ–ї–∞–≥–∞—О—Й–Є—Е –≥–Є–њ–Њ—В–µ–Ј: —Б–њ–ї–Њ—И–љ–Њ—Б—В–Є —Б—А–µ–і—Л –Є —А–∞–≤–µ–љ—Б—В–≤–∞ –љ—Г–ї—О –љ–∞—З–∞–ї—М–љ—Л—Е (–≤–љ—Г—В—А–µ–љ–љ–Є—Е) –љ–∞–њ—А—П–ґ–µ–љ–Є–є. –Ш—Б–Ї–ї—О—З–µ–љ–Є–µ –≤–љ—Г—В—А–µ–љ–љ–Є—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є –Є–Ј —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є—П –љ–µ –і–∞–µ—В –њ–Њ–ї–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Њ –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ–Љ –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є –Є –і–Є–љ–∞–Љ–Є–Ї–µ –µ–≥–Њ —А–∞–Ј–≤–Є—В–Є—П.
–Ш—Б—Е–Њ–і–љ–Њ–µ (–љ–∞—З–∞–ї—М–љ–Њ–µ) –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ - —Н—В–Њ —Б–Є—Б—В–µ–Љ–∞ –њ—А–Є—А–Њ–і–љ—Л—Е (–µ—Б—В–µ—Б—В–≤–µ–љ–љ—Л—Е) –≤–љ—Г—В—А–µ–љ–љ–µ —Г—А–∞–≤–љ–Њ–≤–µ—И–µ–љ–љ—Л—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є –≤ —В–≤–µ—А–і–Њ–Љ —В–µ–ї–µ (—Б—А–µ–і–µ).
–Э–∞–њ—А—П–ґ–µ–љ–љ–Њ-–і–Є—Б–ї–Њ—Ж–Є—А—Г–µ–Љ–Њ–µ (–≤–Њ–Ј–±—Г–ґ–і–µ–љ–љ–Њ–µ) —Б–Њ—Б—В–Њ—П–љ–Є–µ, —Б–Њ–Ј–і–∞–љ–љ–Њ–µ —Б–ї–Њ–ґ–µ–љ–Є–µ–Љ –≤–љ–µ—И–љ–Є—Е —Б–Є–ї–Њ–≤—Л—Е –≤–Њ–Ј–і–µ–є—Б—В–≤–Є–є –Є –≤–љ—Г—В—А–µ–љ–љ–Є—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є –Њ—В —В–µ–Љ–њ–µ—А–∞—В—Г—А–љ—Л—Е, —Е–Є–Љ–Є—З–µ—Б–Ї–Є—Е –Є —Б–Є–ї–Њ–≤—Л—Е —Д–∞–Ї—В–Њ—А–Њ–≤.
–Ш–Ј–Љ–µ–љ–µ–љ–љ–Њ–µ (–Њ—Б—В–∞—В–Њ—З–љ–Њ–µ) –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ, –≤–Њ–Ј–љ–Є–Ї—И–µ–µ –њ–Њ—Б–ї–µ –Є—Б–Ї–ї—О—З–µ–љ–Є—П –Є–ї–Є –Њ—Б–ї–∞–±–ї–µ–љ–Є—П —Б–Є–ї–Њ–≤–Њ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П (—А–∞–Ј–≥—А—Г–Ј–Ї–Є).
–Я—А–Є–Њ–±—А–µ—В–µ–љ–љ–Њ–µ (–Њ—Б—В–∞—В–Њ—З–љ–Њ–µ) –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ, —Б—Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–Њ–µ –њ–Њ–і –≤–ї–Є—П–љ–Є–µ–Љ –≥–µ–Њ—Е–Є–Љ–Є—З–µ—Б–Ї–Є—Е, –≥–µ–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є—Е –Є –≥–µ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є—Е —А–µ–ї–∞–Ї—Б–∞—Ж–Є–Њ–љ–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤.
–Ґ–µ–Њ—А–Є—П –њ—А–Њ—З–љ–Њ—Б—В–Є –Ъ—Г–ї–Њ–љ–∞-–Ь–Њ—А–∞, —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–∞—П —Г—Б–ї–Њ–≤–Є—П –њ—А–µ–і–µ–ї—М–љ–Њ–≥–Њ –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П –Є—Б—Е–Њ–і—П –Є–Ј –њ—А–Є–љ—П—В—Л—Е –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –њ–Њ—Б—В—А–Њ–µ–љ–Є–є, –≤ –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П –њ–Њ–і–≤–µ—А–≥–∞–µ—В—Б—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ–є –Ї—А–Є—В–Є–Ї–µ, —В.–Ї. —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В —Б–ї–Њ–ґ–љ—Л–є —Е–∞—А–∞–Ї—В–µ—А –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В –љ–∞–њ—А—П–ґ–µ–љ–Є–є –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –њ—А–Њ—З–љ–Њ—Б—В–Є.
–Т –њ—А–Њ—З–љ–Њ—Б—В–љ–Њ–є —В–µ–Њ—А–Є–Є –љ–∞–њ—А—П–ґ–µ–љ–Є–є –Њ—Б–љ–Њ–≤–љ—Л–Љ —Г—Б–ї–Њ–≤–Є–µ–Љ —П–≤–ї—П–µ—В—Б—П –њ–Њ–ї—Г—З–µ–љ–Є–µ –њ—А–Њ—Б—В—Л—Е –њ—А—П–Љ–Њ–ї–Є–љ–µ–є–љ—Л—Е –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–µ–є, —Б–Њ–≥–ї–∞—Б—Г—О—Й–Є—Е—Б—П —Б —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ–Є. –≠—В–Њ –і–Њ—Б—В–Є–≥–∞–µ—В—Б—П –љ–Њ–≤—Л–Љ–Є –њ—А–Є–µ–Љ–∞–Љ–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –њ–Њ—Б—В—А–Њ–µ–љ–Є–є –њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —Б–і–≤–Є–≥–∞ –Є –Ї—А—Г–≥–Њ–≤ –љ–∞–њ—А—П–ґ–µ–љ–Є–є.
–Я—А–Є
—Б–ї–Њ–ґ–љ–Њ–Љ –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є (![]() ) –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ –Ї—А—Г–≥–Њ–≤ –љ–∞–њ—А—П–ґ–µ–љ–Є–є –Є
–њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —Б–і–≤–Є–≥–∞ –≤–µ–і–µ—В—Б—П –њ–Њ —Б—Е–µ–Љ–µ —А–Є—Б. 1.–С., –Ї–Њ–≥–і–∞ –Ј–љ–∞—З–µ–љ–Є—П
) –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ –Ї—А—Г–≥–Њ–≤ –љ–∞–њ—А—П–ґ–µ–љ–Є–є –Є
–њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —Б–і–≤–Є–≥–∞ –≤–µ–і–µ—В—Б—П –њ–Њ —Б—Е–µ–Љ–µ —А–Є—Б. 1.–С., –Ї–Њ–≥–і–∞ –Ј–љ–∞—З–µ–љ–Є—П![]() , –Њ—В–Ї–ї–∞–і—Л–≤–∞—О—В—Б—П
–Њ—В –Ї–Њ–љ—Ж–∞ –Њ—В—А–µ–Ј–Ї–∞
, –Њ—В–Ї–ї–∞–і—Л–≤–∞—О—В—Б—П
–Њ—В –Ї–Њ–љ—Ж–∞ –Њ—В—А–µ–Ј–Ї–∞![]() , —А–∞–≤–љ–Њ–≥–Њ –њ–Њ–ї—Г—Б—Г–Љ–Љ–µ –њ–Њ–њ–µ—А–µ—З–љ—Л—Е
–љ–∞–њ—А—П–ґ–µ–љ–Є–є
, —А–∞–≤–љ–Њ–≥–Њ –њ–Њ–ї—Г—Б—Г–Љ–Љ–µ –њ–Њ–њ–µ—А–µ—З–љ—Л—Е
–љ–∞–њ—А—П–ґ–µ–љ–Є–є ![]() –Є
–Є
![]() —Б –њ–Њ–њ—А–∞–≤–Ї–Њ–є
–љ–∞ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ —Ж–µ–љ—В—А–∞ –љ–∞ —Г–≥–Њ–ї φ, —В–Њ–≥–і–∞
—Б –њ–Њ–њ—А–∞–≤–Ї–Њ–є
–љ–∞ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ —Ж–µ–љ—В—А–∞ –љ–∞ —Г–≥–Њ–ї φ, —В–Њ–≥–і–∞
![]()
![]() ;  (1)
;  (1)
–≥–і–µ![]() .
.
–Т
—Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –њ—А–µ–і–µ–ї—М–љ–∞—П –ї–Є–љ–Є—П —Б–і–≤–Є–≥–∞, —Б–µ–Ї—Г—Й–∞—П –Ї—А—Г–≥–Є –љ–∞–њ—А—П–ґ–µ–љ–Є–є, –≤ —В–Њ—З–Ї–∞—Е —Б
τmax, –±—Г–і–µ—В –њ—А—П–Љ–Њ–є –≤ –њ—А–µ–і–µ–ї–∞—Е ![]() ≤
≤ ![]() (–Њ–і–љ–Њ–Њ—Б–љ–Њ–≥–Њ —Б–ґ–∞—В–Є—П). –£—А–∞–≤–љ–µ–љ–Є–µ —Н—В–Њ–є
–њ—А—П–Љ–Њ–є, –њ—А–Є –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–µ
(–Њ–і–љ–Њ–Њ—Б–љ–Њ–≥–Њ —Б–ґ–∞—В–Є—П). –£—А–∞–≤–љ–µ–љ–Є–µ —Н—В–Њ–є
–њ—А—П–Љ–Њ–є, –њ—А–Є –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–µ ![]() –Є
–Є ![]() –Є–Ј (I) –≤ —Д–Њ—А–Љ—Г–ї—Г –Ъ—Г–ї–Њ–љ–∞
–Є–Ј (I) –≤ —Д–Њ—А–Љ—Г–ї—Г –Ъ—Г–ї–Њ–љ–∞
![]()  (2)
 (2)
–±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і:
![]() ,  (3)
,  (3)
–≥–і–µ tg φ - –Љ–Њ–і—Г–ї—М —В—А–µ–љ–Є—П; —Б v —Б—Ж–µ–њ–ї–µ–љ–Є–µ —Б–≤—П–Ј–љ–Њ—Б—В–Є, —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–µ–µ –љ–∞—З–∞–ї—М–љ–Њ–µ —В—А–µ–љ–Є–µ —Б–Ї–Њ–ї—М–ґ–µ–љ–Є–µ.
–Т
—Г—Б–ї–Њ–≤–Є—П—Е –Њ—Б–µ–≤–Њ–є —Б–Є–Љ–Љ–µ—В—А–Є–Є (![]() ) —Г—А–∞–≤–љ–µ–љ–Є—П (1) –њ—А–Є–Њ–±—А–µ—В–∞—О—В –≤–Є–і:
) —Г—А–∞–≤–љ–µ–љ–Є—П (1) –њ—А–Є–Њ–±—А–µ—В–∞—О—В –≤–Є–і:
![]() ,
,
![]() . (4)
. (4)
–Ю—В—Б—О–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —Б–і–≤–Є–≥–∞ –Ј–∞–њ–Є—И–µ—В—Б—П:
![]() .  (5)
.  (5)
–Я—А–Є –Њ–і–љ–Њ–Њ—Б–љ–Њ–Љ —Б–ґ–∞—В–Є–Є –Є–Љ–µ–µ–Љ:
![]() .  (6)
.  (6)
–Я—А–Є —А–µ–ґ–Є–Љ–µ –њ—А–µ–Њ–і–Њ–ї–µ–љ–Є—П "—Г–њ—А—Г–≥–Є—Е" —Б–≤—П–Ј–µ–є, –њ—А–Є –Њ–і–љ–Њ–Њ—Б–љ–Њ–Љ —Б–ґ–∞—В–Є–Є,
![]()  (7)
 (7)
–∞
–њ—А–Є —Б–ї–Њ–ґ–љ–Њ–Љ –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є, –≥–і–µ ![]() —А–µ–ґ–Є–Љ –њ—А–µ–Њ–і–Њ–ї–µ–љ–Є—П —Б—В—А—Г–Ї—В—Г—А–љ—Л—Е —Б–≤—П–Ј–µ–є
–±—Г–і–µ—В –њ—А–Њ–Є—Б—Е–Њ–і–Є—В—М –Ї–Њ–≥–і–∞:
—А–µ–ґ–Є–Љ –њ—А–µ–Њ–і–Њ–ї–µ–љ–Є—П —Б—В—А—Г–Ї—В—Г—А–љ—Л—Е —Б–≤—П–Ј–µ–є
–±—Г–і–µ—В –њ—А–Њ–Є—Б—Е–Њ–і–Є—В—М –Ї–Њ–≥–і–∞:
![]()  (8)
 (8)
–Т–љ—Г—В—А–µ–љ–љ–µ
—Г—А–∞–≤–љ–Њ–≤–µ—И–µ–љ–љ–Њ–µ –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ (–Њ—Б—В–∞—В–Њ—З–љ—Л–µ –љ–∞–њ—А—П–ґ–µ–љ–Є—П), –≤ —Г—Б–ї–Њ–≤–Є—П—Е ![]() —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г–µ—В—Б—П
–љ–∞–њ—А—П–ґ–µ–љ–Є—П–Љ–Є –Њ—В–Ї–ї–∞–і—Л–≤–∞–µ–Љ—Л–Љ–Є –љ–∞ –Њ—В—А–µ–Ј–Ї–µ "–і–∞–≤–ї–µ–љ–Є–µ —Б–≤—П–Ј–љ–Њ—Б—В–Є" (–С–Ю –њ–Њ
—Б—Е–µ–Љ–µ —А–Є—Б.1.–С.)
—Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г–µ—В—Б—П
–љ–∞–њ—А—П–ґ–µ–љ–Є—П–Љ–Є –Њ—В–Ї–ї–∞–і—Л–≤–∞–µ–Љ—Л–Љ–Є –љ–∞ –Њ—В—А–µ–Ј–Ї–µ "–і–∞–≤–ї–µ–љ–Є–µ —Б–≤—П–Ј–љ–Њ—Б—В–Є" (–С–Ю –њ–Њ
—Б—Е–µ–Љ–µ —А–Є—Б.1.–С.)
![]()
![]()  (9)
 (9)
–†–∞—Б—В—П–ґ–µ–љ–Є–µ
—А–µ–∞–ї–Є–Ј—Г–µ—В—Б—П –љ–∞ –њ—А–µ–Њ–і–Њ–ї–µ–љ–Є–µ —Б–Є–ї —Б–≤—П–Ј–љ–Њ—Б—В–Є –Є –≤–µ–і–µ—В –Ї –Њ—Б–ї–∞–±–ї–µ–љ–Є—О —Б—Ж–µ–њ–ї–µ–љ–Є—П
—Б–≤—П–Ј–љ–Њ—Б—В–Є. –†–∞—Б—В—П–≥–Є–≤–∞—О—Й–µ–µ –љ–∞–њ—А—П–ґ–µ–љ–Є–µ ![]() –Њ—В–Ї–ї–∞–і—Л–≤–∞–µ—В—Б—П –њ–Њ –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–Њ–Љ—Г
–љ–∞–њ—А–∞–≤–ї–µ–љ–Є—О –Њ—Б–Є
–Њ—В–Ї–ї–∞–і—Л–≤–∞–µ—В—Б—П –њ–Њ –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–Њ–Љ—Г
–љ–∞–њ—А–∞–≤–ї–µ–љ–Є—О –Њ—Б–Є![]() , —Б –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–Љ –њ–µ—А–µ–љ–Њ—Б–Њ–Љ –љ–∞ –Њ—Б—М
, —Б –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–Љ –њ–µ—А–µ–љ–Њ—Б–Њ–Љ –љ–∞ –Њ—Б—М ![]() (—Б–Љ. —Б—Е–µ–Љ—Г —А–Є—Б.1
.–Р.). –°–Њ–≥–ї–∞—Б–љ–Њ –њ—А–Є–љ—П—В–Њ–Љ—Г –њ–Њ—Б—В—А–Њ–µ–љ–Є—О
(—Б–Љ. —Б—Е–µ–Љ—Г —А–Є—Б.1
.–Р.). –°–Њ–≥–ї–∞—Б–љ–Њ –њ—А–Є–љ—П—В–Њ–Љ—Г –њ–Њ—Б—В—А–Њ–µ–љ–Є—О
![]() .  (10)
.  (10)
–Є–ї–Є
![]() .
.
–Я—А–Њ–Є–Ј–≤–µ–і–µ–љ–Њ
—Г—В–Њ—З–љ–µ–љ–Є–µ –Є—Б—Е–Њ–і–љ—Л—Е —Г—Б–ї–Њ–≤–Є–є –Њ—Б–µ–≤–Њ–≥–Њ —А–∞—Б—В—П–ґ–µ–љ–Є—П ![]() —В—А—Г–±—З–∞—В—Л—Е –Њ–±—А–∞–Ј—Ж–Њ–≤, –љ–∞—Е–Њ–і—П—Й–Є—Е—Б—П –њ–Њ–і
–≤–љ—Г—В—А–µ–љ–љ–Є–Љ –і–∞–≤–ї–µ–љ–Є–µ–Љ
—В—А—Г–±—З–∞—В—Л—Е –Њ–±—А–∞–Ј—Ж–Њ–≤, –љ–∞—Е–Њ–і—П—Й–Є—Е—Б—П –њ–Њ–і
–≤–љ—Г—В—А–µ–љ–љ–Є–Љ –і–∞–≤–ї–µ–љ–Є–µ–Љ![]() :
:
![]() ,  (11)
,  (11)
![]() ,
,
–≥–і–µ![]() ,
, ![]() —Б–Љ. (1), –Ј–і–µ—Б—М –Ј–љ–∞–Ї
—Б–Љ. (1), –Ј–і–µ—Б—М –Ј–љ–∞–Ї
–Љ–Є–љ—Г—Б
–Њ–њ—Г—Й–µ–љ –њ—А–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–Њ–≥–Њ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П –Њ—Б–Є ![]() –і–ї—П —Г–і–Њ–±—Б—В–≤–∞ –љ–∞–њ–Є—Б–∞–љ–Є—П –Є
—А–∞—Б—З–µ—В–Њ–≤.
–і–ї—П —Г–і–Њ–±—Б—В–≤–∞ –љ–∞–њ–Є—Б–∞–љ–Є—П –Є
—А–∞—Б—З–µ—В–Њ–≤.
–Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —А–∞—Б—В—П–ґ–µ–љ–Є—П, –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ (3), –±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і
![]() .  (12)
.  (12)
–≥–і–µ
![]() –Є
–Є![]() - –њ–∞—А–∞–Љ–µ—В—А—Л
–њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —А–∞—Б—В—П–ґ–µ–љ–Є—П –≤ —Г—Б–ї–Њ–≤–Є—П—Е —Б–ї–Њ–ґ–љ–Њ–≥–Њ –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П,
–∞–љ–∞–ї–Њ–≥–Є—З–љ—Л–µ —Б—Ж–µ–њ–ї–µ–љ–Є—О –Є —Г–≥–ї—Г –≤–љ—Г—В—А–µ–љ–љ–µ–≥–Њ —В—А–µ–љ–Є—П.
- –њ–∞—А–∞–Љ–µ—В—А—Л
–њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —А–∞—Б—В—П–ґ–µ–љ–Є—П –≤ —Г—Б–ї–Њ–≤–Є—П—Е —Б–ї–Њ–ґ–љ–Њ–≥–Њ –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П,
–∞–љ–∞–ї–Њ–≥–Є—З–љ—Л–µ —Б—Ж–µ–њ–ї–µ–љ–Є—О –Є —Г–≥–ї—Г –≤–љ—Г—В—А–µ–љ–љ–µ–≥–Њ —В—А–µ–љ–Є—П.
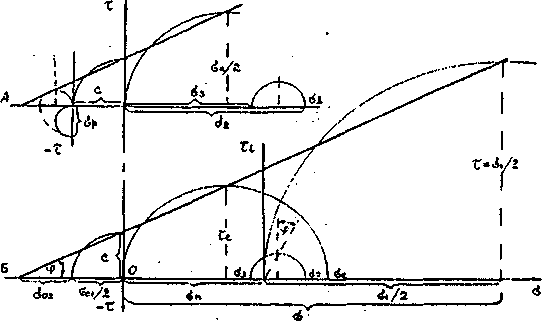
–†–Є—Б. 1. –°—Е–µ–Љ—Л –њ–Њ—Б—В—А–Њ–µ–љ–Є–є –Ї—А—Г–≥–Њ–≤ –љ–∞–њ—А—П–ґ–µ–љ–Є–є –Є –њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —Б–і–≤–Є–≥–∞.
–Р - –≤ —А–µ–ґ–Є–Љ–µ —А–∞—Б—В—П–ґ–µ–љ–Є—П: –С - –њ—А–Є —Б–ї–Њ–ґ–љ–Њ–Љ –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є.
–Т—Л—А–∞–Ј–Є–≤
–≤–љ—Г—В—А–µ–љ–љ–µ–µ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–µ cp —З–µ—А–µ–Ј —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–µ –Њ–і–љ–Њ–Њ—Б–љ–Њ–≥–Њ —А–∞—Б—В—П–ґ–µ–љ–Є—П![]() , –њ–Њ–і–Њ–±–љ–Њ (6),
–Є–Љ–µ–µ–Љ:
, –њ–Њ–і–Њ–±–љ–Њ (6),
–Є–Љ–µ–µ–Љ:
![]() ,  (13)
,  (13)
–Њ—В–Ї—Г–і–∞
![]()  (14)
 (14)
–Я—А–Є–љ—П—В—Л–µ —Б—Е–µ–Љ—Л –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —Б–і–≤–Є–≥–∞ –Є –Ї—А—Г–≥–Њ–≤ –љ–∞–њ—А—П–ґ–µ–љ–Є–є –њ–Њ–Ј–≤–Њ–ї–Є–ї–Є —Г—Б—В–∞–љ–Њ–≤–Є—В—М —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї—М–љ—Л–µ —Б–≤—П–Ј–Є –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В –љ–∞–њ—А—П–ґ–µ–љ–Є–є –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –њ—А–Њ—З–љ–Њ—Б—В–Є —Б –Є φ –≤ —А–∞–Ј–љ—Л—Е —Б—В–∞–і–Є—П—Е –Є —А–µ–ґ–Є–Љ–∞—Е –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П: –≤ –Є—Б—Е–Њ–і–љ–Њ–Љ, –≤–љ—Г—В—А–µ–љ–љ–µ —Г—А–∞–≤–љ–Њ–≤–µ—И–µ–љ–љ–Њ–Љ; –њ—А–Є –њ—А–µ–Њ–і–Њ–ї–µ–љ–Є–Є —Г–њ—А—Г–≥–Є—Е –Є –њ—А–µ–і–µ–ї—М–љ—Л—Е —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–є –Њ—В –≤–љ–µ—И–љ–Є—Е –≤–Њ–Ј–і–µ–є—Б—В–≤–Є–є; –≤ —А–µ–ґ–Є–Љ–∞—Е –Њ–і–љ–Њ–Њ—Б–љ–Њ–≥–Њ —Б–ґ–∞—В–Є—П –Є —А–∞—Б—В—П–ґ–µ–љ–Є—П. –Т—Б–µ –Њ—Б–љ–Њ–≤–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П –њ—А–Њ–≤–µ—А–µ–љ—Л –њ–Њ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ –Є—Б–њ—Л—В–∞–љ–Є–є —А–∞–Ј–љ–Њ—А–Њ–і–љ—Л—Е –Љ–∞—В–µ—А–Є–∞–ї–Њ–≤ –Є –њ–Њ–Ї–∞–Ј–∞–ї–Є —Г–і–Њ–≤–ї–µ—В–≤–Њ—А–Є—В–µ–ї—М–љ—Г—О –і–ї—П –њ—А–∞–Ї—В–Є–Ї–Є —Б—В–µ–њ–µ–љ—М —Б—Е–Њ–і–Є–Љ–Њ—Б—В–Є –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –Є–Ј–≤–µ—Б—В–љ—Л–Љ–Є —А–µ—И–µ–љ–Є—П–Љ–Є.
–Т–∞–ґ–љ—Л–Љ –і–Њ—Б—В–Є–ґ–µ–љ–Є–µ–Љ, –њ–Њ–і–Ї—А–µ–њ–ї–µ–љ–љ—Л–Љ –Њ–њ—Л—В–љ—Л–Љ–Є –і–∞–љ–љ—Л–Љ–Є, —П–≤–ї—П–µ—В—Б—П –њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –Њ —В–Њ–Љ, —З—В–Њ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –љ–∞–њ—А—П–ґ–µ–љ–Є—П —Б–Њ—Б—В–∞–≤–ї—П—О—В –њ–Њ–ї–Њ–≤–Є–љ—Г –Њ—В –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ—Л—Е –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є. –Ш–Ј–≤–µ—Б—В–љ–Њ–µ –ґ–µ –Є—Е —А–∞–≤–µ–љ—Б—В–≤–Њ –њ–Њ–ї—Г—А–∞–Ј–љ–Њ—Б—В–Є –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є –≤–µ–і–µ—В –Ї –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В–Є –њ—А–µ–і–µ–ї—М–љ–Њ–є –ї–Є–љ–Є–Є —Б–і–≤–Є–≥–∞ –Є –Ј–∞—В—А—Г–і–љ—П–µ—В —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ–Є–µ —Б–≤—П–Ј–µ–є –Љ–µ–ґ–і—Г —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л–Љ–Є –њ–∞—А–∞–Љ–µ—В—А–∞–Љ–Є –љ–∞–њ—А—П–ґ–µ–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П.
–°–Њ–њ–Њ—Б—В–∞–≤–ї–µ–љ–Є–µ —А–∞–Ј–ї–Є—З–љ—Л—Е —В–µ–Њ—А–Є–є
| –Я–Њ —Г—Б–ї–Њ–≤–Є—О –њ—А–Њ—З–љ–Њ—Б—В–Є –∞–≤—В–Њ—А–∞ | –Я–Њ –Ъ—Г–ї–Њ–љ—Г-–Ь–Њ—А—Г-–•–Є–ї–ї—Г |
|
1. –У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ –њ—А–µ–і–µ–ї—М–љ—Л—Е
–ї–Є–љ–Є–є —Б–і–≤–Є–≥–∞ (–Я–Ы–°) –љ–µ –Љ–µ–љ–µ–µ —З–µ–Љ –њ–Њ 2-3 —В–Њ—З–Ї–∞–Љ –њ—А–Є |
|
|
1.1. –†–∞–Ј–Љ–µ—А—Л 1.2. –Ъ–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–µ–Ї –Я–Ы–° –љ–∞—Е–Њ–і—П—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–∞–Љ: |
1.1. –Т—Б–µ —А–∞–Ј–Љ–µ—А—Л 1.2. |
|
2. –Т–Є–і –Я–Ы–° –њ–Њ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ
–Ј–љ–∞—З–µ–љ–Є—П–Љ |
|
|
2.1. –Я—А—П–Љ–∞—П –≤ –њ—А–µ–і–µ–ї–∞—Е |
2.1. –Я—А—П–Љ–∞—П –≤ –њ—А–µ–і–µ–ї–∞—Е |
|
3. –У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ –Я–Ы–° –љ–µ
–Љ–µ–љ–µ–µ —З–µ–Љ –њ–Њ 2-3 —В–Њ—З–Ї–∞–Љ –њ—А–Є |
|
|
3.1. –Я–Њ—Б—В—А–Њ–µ–љ–Є–µ –њ—А–Є 3.2.
|
3.1. –Э–µ—В. 3.2. –Э–µ—В —А–µ—И–µ–љ–Є—П. |
|
4. –Т–Є–і –Я–Ы–° –њ–Њ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ
–Ј–љ–∞—З–µ–љ–Є—П–Љ |
|
|
4. 1. –Я—А—П–Љ–∞—П –≤ –њ—А–µ–і–µ–ї–∞—Е |
4.1. –Э–µ—В. |
| 5. –†–µ—И–µ–љ–Є—П –Є –њ—А–Њ–≥–љ–Њ–Ј—Л | |
|
5.1. –Ю–і–љ–Њ–Ј–љ–∞—З–љ–Њ–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –њ—А–Њ—З–љ–Њ—Б—В–Є
(–њ–∞—А–∞–Љ–µ—В—А–Њ–≤ 5.2. –Ю—Б—В–∞—В–Њ—З–љ—Л–µ –љ–∞–њ—А—П–ґ–µ–љ–Є—П
–Њ—В–Њ–ґ–і–µ—Б—В–≤–ї—П—О—В—Б—П —Б L–і–∞–≤–ї–µ–љ–Є–µ–Љ —Б–≤—П–Ј–љ–Њ—Б—В–Є¬¶ 5.3. –°–≤—П–Ј—М –Љ–µ–ґ–і—Г –Њ–і–љ–Њ–Њ—Б–љ—Л–Љ —Б–ґ–∞—В–Є–µ–Љ 5.4. –Я—А–Њ–≥–љ–Њ–Ј–Є—А—Г–µ—В—Б—П –њ—А–µ–і—И–µ—Б—В–≤—Г—О—Й–µ–µ –і–∞–≤–ї–µ–љ–Є–µ –Є—Б–њ—Л—В–∞–љ–љ–Њ–µ –Љ–∞—В–µ—А–Є–∞–ї–Њ–Љ –Є —Б—В–µ–њ–µ–љ—М –µ–≥–Њ —А–µ–ї–∞–Ї—Б–∞—Ж–Є–Є. 5.5. –Э–∞–њ—А—П–ґ–µ–љ–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ –Ј–µ–Љ–љ–Њ–є –Ї–Њ—А—Л –Њ–±—Г—Б–ї–Њ–≤–ї–µ–љ–Њ –Њ—Б—В–∞—В–Њ—З–љ—Л–Љ–Є –љ–∞–њ—А—П–ґ–µ–љ–Є—П–Љ–Є –Є –њ—А–Є–≥—А—Г–Ј–Ї–Њ–є –≤—Л—И–µ–ї–µ–ґ–∞—Й–Є—Е –њ–Њ—А–Њ–і. 5.6. –Ю–њ—А–µ–і–µ–ї—П–µ–Љ—Л–µ –њ–∞—А–∞–Љ–µ—В—А—Л –њ—А–Њ—З–љ–Њ—Б—В–Є 5.7. –Ю–і–љ–Њ–Ј–љ–∞—З–љ–Њ–µ –њ—А–Њ–≥–љ–Њ–Ј–Є—А–Њ–≤–∞–љ–Є–µ –Њ–њ–Њ–ї–Ј–љ–µ–≤—Л—Е —Б–Ї–ї–Њ–љ–Њ–≤ –≤ —Б–Њ—Б—В–Њ—П–љ–Є–Є –і–ї–Є—В–µ–ї—М–љ–Њ–є –Є –њ—А–µ–і–µ–ї—М–љ–Њ–є —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є. |
5.1. –£–≥–Њ–ї 5.2. –Э–µ —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞—О—В—Б—П. 5.3. –Э–µ —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В—Б—П. 5.4. –Э–µ —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В—Б—П. 5.5. –Ю—В–Љ–µ—З–∞–µ—В—Б—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ–µ —А–∞—Б—Е–Њ–ґ–і–µ–љ–Є–µ –≤ –Ј–љ–∞—З–µ–љ–Є—П—Е –Ї–∞—Б–∞—В–µ–ї—М–љ—Л—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є. 5.6. –°—В–µ–њ–µ–љ—М —Б–Њ–њ–Њ—Б—В–∞–≤–Є–Љ–Њ—Б—В–Є –±–Њ–ї–µ–µ –љ–Є–Ј–Ї–∞—П. 5.7. –Т–∞—А–Є–∞–љ—В–љ–Њ–µ –њ—А–Њ–≥–љ–Њ–Ј–Є—А–Њ–≤–∞–љ–Є–µ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є. |
–°–њ–Є—Б–Њ–Ї –ї–Є—В–µ—А–∞—В—Г—А—Л