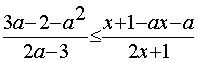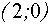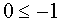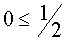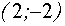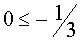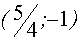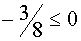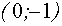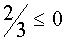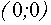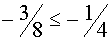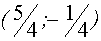Реферат: Графическое решение уравнений, неравенств, систем с параметром
I. Введение
II. Уравнения с параметрами.
§ 1. Определения.
§ 2. Алгоритм решения.
§ 3. Примеры.
III. Неравенства с параметрами.
§ 1. Определения.
§ 2. Алгоритм решения.
§ 3. Примеры.
IV. Список литературы.
ВведениеИзучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Некоторые Вузы также включают в экзаменационные билеты уравнения, неравенства и их системы, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. В школе же этот один из наиболее трудных разделов школьного курса математики рассматривается только на немногочисленных факультативных занятиях.
Готовя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. На мой взгляд графический метод является удобным и быстрым способом решения уравнений и неравенств с параметрами.
В моём реферате рассмотрены часто встречающиеся типы уравнений, неравенств и их систем, и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов и при поступлении а ВУЗ.
§ 1. Основные определенияРассмотрим уравнение
¦ (a, b, c, …, k , x)=j (a, b, c, …, k , x), (1)
где a, b, c, …, k , x -переменные величины.
Любая система значений переменных
а = а0, b = b0, c = c0, …, k = k0, x = x0,
при которой и левая и правая части этого уравнения принимают действительные значения, называется системой допустимых значений переменных a, b, c, …, k , x. Пусть А – множество всех допустимых значений а, B – множество всех допустимых значений b, и т.д., Х – множество всех допустимых значений х, т.е. аÎ А, bÎ B, …, xÎ X. Если у каждого из множеств A, B, C, …, K выбрать и зафиксировать соответственно по одному значению a, b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным.
Переменные a, b, c, …, k , которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры.
Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k , l, m, n а неизвестные – буквами x, y,z.
Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.
Два уравнения, содержащие одни и те же параметры, называются равносильными, если:
а) они имеют смысл при одних и тех же значениях параметров;
б) каждое решение первого уравнения является решением второго и наоборот.
§ 2. Алгоритм решения. Находим область определения уравнения. Выражаем a как функцию от х. В системе координат хОа строим график функции а=¦ (х) для тех значений х, которые входят в область определения данного уравнения.Находим точки пересечения прямой а=с, где сÎ (-¥ ;+¥ ) с графиком функции а=¦ (х).Если прямая а=с пересекает график а=¦ (х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а=¦ (х) относительно х.
Записываем ответ. § 3. ПримерыI. Решить уравнение
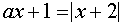 (1)
(1)
Решение.
Поскольку х=0 не является корнем уравнения, то можно разрешить уравнение относительно а :
 или
или 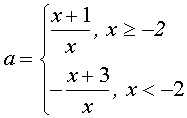
График функции – две “склеенных” гиперболы. Количество решений исходного уравнения определяется количеством точек пересечения построенной линии и прямой у=а.
Если а Î
(-¥
;-1]È
(1;+¥
)È
 , то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения
, то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения  относительно х.
относительно х.
Таким образом, на этом промежутке уравнение (1) имеет решение 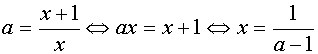 .
.
Если а Î
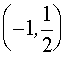 , то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений
, то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений 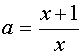 и
и 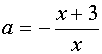 , получаем
, получаем
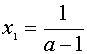 и
и 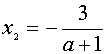 .
.
Если а Î
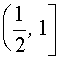 , то прямая у=а не пересекает график уравнения (1), следовательно решений нет.
, то прямая у=а не пересекает график уравнения (1), следовательно решений нет.
Ответ:
Если а Î
(-¥
;-1]È
(1;+¥
)È
 , то
, то 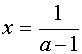 ;
;
Если а Î 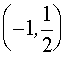 ,
то
,
то 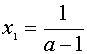 ,
, 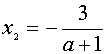 ;
;
Если а Î
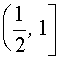 , то решений нет.
, то решений нет.
II. Найти все значения параметра а, при которых уравнение 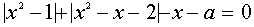 имеет три различных корня.
имеет три различных корня.
Решение.
Переписав уравнение в виде 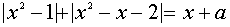 и рассмотрев пару функций
и рассмотрев пару функций  , можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции
, можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции 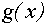 , при которых он имеет точно три точки пересечения с графиком функции
, при которых он имеет точно три точки пересечения с графиком функции 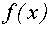 .
.
В системе координат хОу построим график функции 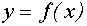 ). Для этого можно представить её в виде
). Для этого можно представить её в виде 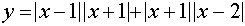 и, рассмотрев четыре возникающих случая, запишем эту функцию в виде
и, рассмотрев четыре возникающих случая, запишем эту функцию в виде
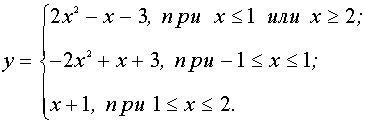
Поскольку график функции 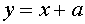 – это прямая, имеющая угол наклона к оси Ох, равный
– это прямая, имеющая угол наклона к оси Ох, равный  , и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции
, и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции 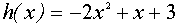 . Поэтому находим производную
. Поэтому находим производную 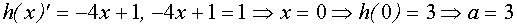
Ответ: 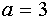 .
.
III. Найти все значения параметра а, при каждом из которых система уравнений
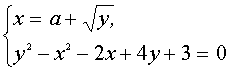
имеет решения.
Решение.
Из первого уравнения системы получим 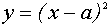 при
при 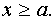 Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы
Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы 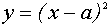 “скользят” вершинами по оси абсцисс.
“скользят” вершинами по оси абсцисс.
Выделим в левой части второго уравнения полные квадраты и разложим её на множители
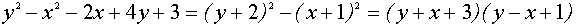
Множеством точек плоскости 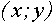 , удовлетворяющих второму уравнению, являются две прямые
, удовлетворяющих второму уравнению, являются две прямые
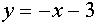 и
и 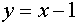
Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.
Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается
прямой 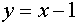 ), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то
), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то 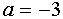 .
.
Случай касания “полупараболы” с прямой 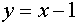 определим из условия существования единственного решения системы
определим из условия существования единственного решения системы
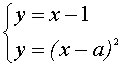
В этом случае уравнение
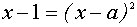
имеет один корень, откуда находим :
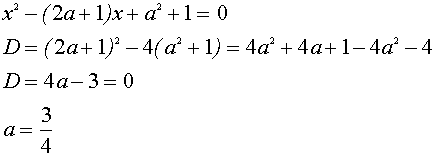
Следовательно, исходная система не имеет решений при  , а при
, а при 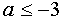 или
или 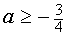 имеет хотя бы одно решение.
имеет хотя бы одно решение.
Ответ: а Î
(-¥
;-3] È
(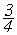 ;+¥
).
;+¥
).
IV. Решить уравнение
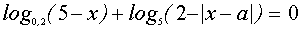
Решение.
Использовав равенство  , заданное уравнение перепишем в виде
, заданное уравнение перепишем в виде
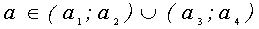
Это уравнение равносильно системе
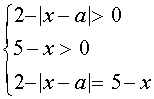
Уравнение 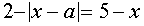 перепишем в виде
перепишем в виде
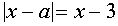 . (*)
. (*)
Последнее уравнение проще всего решить, используя геометрические соображения. Построим графики функций  и
и  Из графика следует, что при
Из графика следует, что при 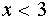 графики не пересекаются и, следовательно, уравнение не имеет решений.
графики не пересекаются и, следовательно, уравнение не имеет решений.
Если 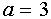 , то при
, то при 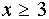 графики функций совпадают и, следовательно, все значения
графики функций совпадают и, следовательно, все значения 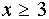 являются решениями уравнения (*).
являются решениями уравнения (*).
При 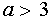 графики пересекаются в одной точке, абсцисса которой
графики пересекаются в одной точке, абсцисса которой 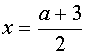 . Таким образом, при
. Таким образом, при 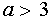 уравнение (*) имеет единственное решение -
уравнение (*) имеет единственное решение - 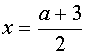 .
.
Исследуем теперь, при каких значениях а найденные решения уравнения (*) будут удовлетворять условиям
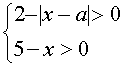
Пусть 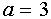 , тогда
, тогда 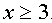 . Система примет вид
. Система примет вид
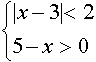
Её решением будет промежуток хÎ (1;5). Учитывая,
что 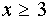 , можно заключить, что при
, можно заключить, что при
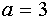 исходному уравнению удовлетворяют
все значения х из промежутка [3; 5).
исходному уравнению удовлетворяют
все значения х из промежутка [3; 5).
Рассмотрим случай, когда  . Система неравенств примет вид
. Система неравенств примет вид
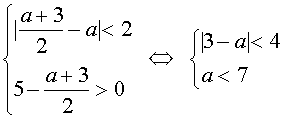
Решив эту систему, найдем аÎ
(-1;7). Но 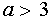 , поэтому при аÎ
(3;7) исходное уравнение имеет единственное решение
, поэтому при аÎ
(3;7) исходное уравнение имеет единственное решение 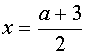 .
.
Ответ:
если аÎ (-¥ ;3), то решений нет;
если а=3, то хÎ [3;5);
если aÎ
(3;7), то 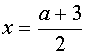 ;
;
если aÎ [7;+ ¥ ), то решений нет.
V. Решить уравнение
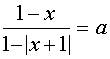 , где а - параметр. (5)
, где а - параметр. (5)
Решение.
При любом а :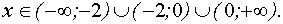 Если
Если 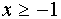 , то
, то 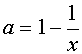 ;
;
если 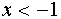 , то
, то 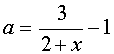 .
.
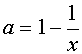 , выделяем ту его часть , которая соответствует
, выделяем ту его часть , которая соответствует  . Затем отметим ту часть графика функции
. Затем отметим ту часть графика функции 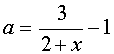 , которая соответствует
, которая соответствует 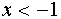 .
По графику определяем, при каких значениях а уравнение (5) имеет решение и при каких – не имеет решения.
.
По графику определяем, при каких значениях а уравнение (5) имеет решение и при каких – не имеет решения.
Ответ:
если 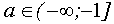 , то
, то 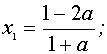
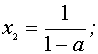
если  , то
, то  ;
;
если 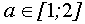 , то решений нет;
, то решений нет;
если 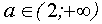 , то
, то 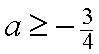 ,
, 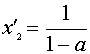 .
.
VI. Каким условиям должны удовлетворять те значения параметров 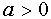 и
и 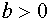 , при которых системы
, при которых системы
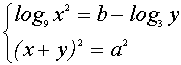 (1)
(1)
и
 (2)
(2)
имеют одинаковое число решений ?
Решение.
С учетом того, что 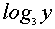 имеет смысл только при
имеет смысл только при 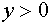 , получаем после преобразований систему
, получаем после преобразований систему
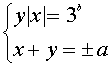 (3)
(3)
равносильную системе (1).
Система (2) равносильна системе
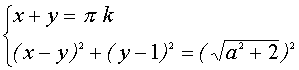 (4)
(4)
Первое уравнение системы (4) задает в плоскости хОу семейство прямых, второе уравнение задает семейство концентрических окружностей с центром в точке А(1;1) и радиусом 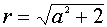
Поскольку 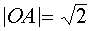 , а
, а 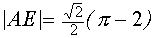 , то
, то 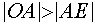 , и, следовательно, система (4) имеет не менее четырех решений. При
, и, следовательно, система (4) имеет не менее четырех решений. При 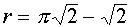 окружность касается прямой
окружность касается прямой 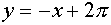 и система (4) имеет пять решений.
и система (4) имеет пять решений.
Таким образом, если 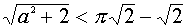 , то система (4) имеет четыре решения, если
, то система (4) имеет четыре решения, если 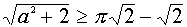 , то таких решений будет больше, чем четыре.
, то таких решений будет больше, чем четыре.
Если же иметь в виду не радиусы окружностей, а сам параметр а, то система (4) имеет четыре решения в случае, когда 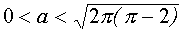 , и больше четырех решений, если
, и больше четырех решений, если 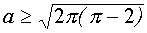 .
.
Обратимся теперь к рассмотрению системы (3). Первое уравнение этой системы задаёт в плоскости хОу семейство гипербол, расположенных в первом и втором квадрантах. Второе уравнение системы (3) задает в плоскости хОу семейство прямых.
При фиксированных положительных а и b система (3) может иметь два, три, или четыре решения. Число же решений зависит от того, будет ли прямая, заданная уравнением 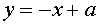 , иметь общие точки с гиперболой
, иметь общие точки с гиперболой 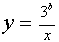 при
при 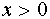 (прямая
(прямая 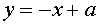 всегда имеет одну точку пересечения с графиком функции
всегда имеет одну точку пересечения с графиком функции 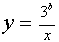 ).
).
Для решения этого рассмотрим уравнение
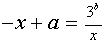 ,
,
которое удобнее переписать в виде

Теперь решение задачи сводится к рассмотрению дискриминанта D последнего уравнения:
если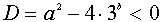 , т.е. если
, т.е. если 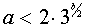 , то система (3) имеет два решения;
если
, то система (3) имеет два решения;
если 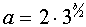 , то система (3) имеет три решения;
если
, то система (3) имеет три решения;
если 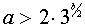 , то система (3) имеет четыре решения.
, то система (3) имеет четыре решения.
Таким образом, одинаковое число решений у систем (1) и (2) – это четыре. И это имеет место, когда 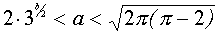 .
.
Ответ: 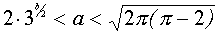
Неравенство
¦ (a, b, c, …, k , x)>j (a, b, c, …, k , x), (1)
где a, b, c, …, k – параметры, а x – действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.
Любая система значений параметров а = а0, b = b0, c = c0, …, k = k0, при некоторой функции
¦ (a, b, c, …, k , x) и
j (a, b, c, …, k , x
имеют смысл в области действительных чисел, называется системой допустимых значений параметров.
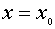 называется допустимым значением х, если
называется допустимым значением х, если
¦ (a, b, c, …, k , x) и
j (a, b, c, …, k , x
принимают действительные значения при любой допустимой системе значений параметров.
Множество всех допустимых значений х называется областью определения неравенства (1).
Действительное число х0 называется частным решением неравенства (1), если неравенство
¦ (a, b, c, …, k , x0)>j (a, b, c, …, k , x0)
верно при любой системе допустимых значений параметров.
Совокупность всех частных решений неравенства (1) называется общим решением этого неравенства.
Решить неравенство (1) – значит указать, при каких значениях параметров существует общее решение и каково оно.
Два неравенства
¦ (a, b, c, …, k , x)>j (a, b, c, …, k , x) и (1)
z (a, b, c, …, k , x)>y (a, b, c, …, k , x) (2)
называются равносильными, если они имеют одинаковые общие решения при одном и том же множестве систем допустимых значений параметров.
§ 2. Алгоритм решения. Находим область определения данного неравенства. Сводим неравенство к уравнению. Выражаем а как функцию от х. В системе координат хОа строим графики функций а =¦ (х) для тех значений х, которые входят в область определения данного неравенства. Находим множества точек, удовлетворяющих данному неравенству. Исследуем влияние параметра на результат. найдём абсциссы точек пересечения графиков. зададим прямую а=соnst и будем сдвигать её от -¥ до+¥ Записываем ответ.Это всего лишь один из алгоритмов решения неравенств с параметрами, с использованием системы координат хОа. Возможны и другие методы решения, с использованием стандартной системы координат хОy.
§ 3. ПримерыI. Для всех допустимых значений параметра а решить неравенство
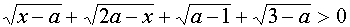
Решение.
В области определения параметра а, определённого системой неравенств

данное неравенство равносильно системе неравенств
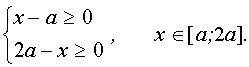
Если 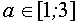 , то решения исходного неравенства заполняют отрезок
, то решения исходного неравенства заполняют отрезок 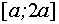 .
.
Ответ: 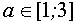 ,
, 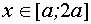 .
.
II. При каких значениях параметра а имеет решение система
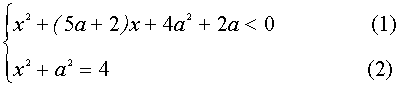
Решение.
Найдем корни трехчлена левой части неравенства –
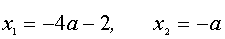 (*)
(*)
Прямые, заданные равенствами (*), разбивают координатную плоскость аОх на четыре области, в каждой из которых квадратный трехчлен
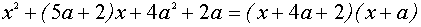
сохраняет постоянный знак. Уравнение (2) задает окружность радиуса 2 с центром в начале координат. Тогда решением исходной системы будет пересечение заштрихован
ной области с окружностью, где 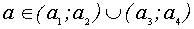 , а значения
, а значения 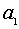 и
и 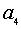 находятся из системы
находятся из системы

а значения 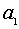 и
и 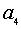 находятся из системы
находятся из системы
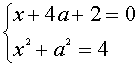
Решая эти системы, получаем, что
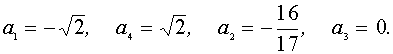
Ответ: 
III. Решить неравенство 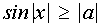 на
на 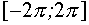 в зависимости от значений параметра а.
в зависимости от значений параметра а.
Решение.
Находим область допустимых значений –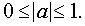 Построим график функции в системе координат хОу.
при
Построим график функции в системе координат хОу.
при 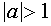 неравенство решений не имеет.
при
неравенство решений не имеет.
при 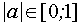 для
для 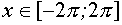 решение х удовлетворяет соотношению
решение х удовлетворяет соотношению 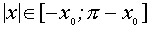 , где
, где 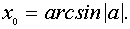
Ответ: Решения неравенства существуют при 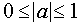
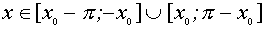 , где
, где  , причем при
, причем при  решения
решения 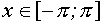 ; при
; при 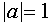 решения
решения 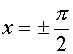 .
.
IV. Решить неравенство
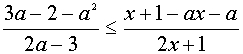
Решение.
Находим ОДЗ или линии разрыва (асимптоты)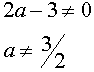
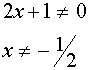
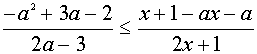
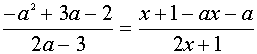
Разложим числитель на множители.
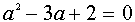
т. к. 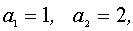 то
то
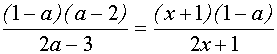
Разделим обе части равенства на 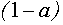 при
при 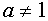 . Но
. Но 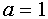 является решением : левая часть уравнения равна правой части и равна нулю при
является решением : левая часть уравнения равна правой части и равна нулю при
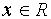 .
.
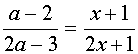
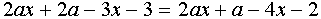
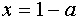
3. Строим в ПСК хОа графики функций
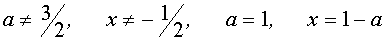
и нумеруем образовавшиеся области (оси роли не играют). Получилось девять областей.
4. Ищем, какая из областей подходит для данного неравенства, для чего берем точку из области и подставляем в неравенство.
Для наглядности составим таблицу.
|
? |
точка |
неравенство: |
вывод |
|
1 |
|
|
- |
|
2 |
|
|
+ |
|
3 |
|
|
- |
|
4 |
|
|
+ |
|
5 |
|
|
- |
|
6 |
|
|
+ |
|
7 |
|
|
- |
|
8 |
|
|
+ |
|
9 |
|
|
- |
5. Найдем точки пересечения графиков
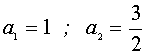
6. Зададим прямую а=сonst и будем сдвигать её от -¥ до +¥ .
Ответ.
при 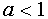
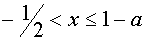
при 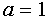
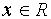
при 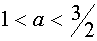
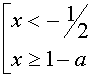
при 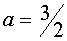 решений нет
решений нет
при 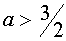
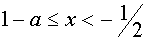
| Самостоятельная работа как средство обучения решению уравнений в 5-9 ... | |
|
... РФ Светлоградский педагогический колледж Дипломная работа Самостоятельная работа как средство обучения решению уравнений в 5 - 9 классах Выполнила: Кроме того, требуется усвоить факт: график линейного уравнения ах + bу= с, где а 0 или b 0, есть прямая линия, а также научиться строить график конкретных линейных уравнений с ... Значит, абсцисса точки пересечения графиков функций y=x2 и y=6/x является корнем уравнения (x2=6/x). Из рисунка видно, что приближенное значение корня равно 1,8. Примененный способ ... |
Раздел: Рефераты по педагогике Тип: реферат |
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... Т: Каковы бы нибыла прямая а и не лежащая на ней точка А , через точку А проходит не меньше двух прямых не пересекающих прямую а. Т: Если у треугольников АВС и А"B"C" равны ... Точкой будема называть любую упорядоченную пару вещ. чисел(х,у). Прямой назовем множество всех точек координаты которых удавлетворяют линейному уравнению ах+by+c=0, (1) a,b R a2+b2 ... |
Раздел: Рефераты по математике Тип: реферат |
| Основы макроэкономики | |
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ... c) пересекает ось объемов реального ВВП; Если кривые IS и LM пересекаются (IS=LM), то в точке их пересечения имеет место совместное равновесие на товарном и денежном рынках. |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Анализ методов определения минимального, максимального значения ... | |
|
Федеральное агентство по образованию Московский государственный открытый университет Чебоксарский политехнический институт Курсовой проект по ... Допустимая точка x* называется условным минимумом функции f0 при ограничениях fi(x) = 0, i = 1, ..., k (или решением задачи (3.1)-(3.2)), если при всех допустимых точках x f0(x ... В самом деле, для нахождения точки (x*, m*) I Rm+k+1, т. е. для нахождения m + k + 1 неизвестных, мы имеем m + k уравнений |
Раздел: Рефераты по информатике, программированию Тип: курсовая работа |
| Кинематический анализ механизма транспортирования ткани | |
|
Кинематический анализ механизма верхней и нижней реек швейной машины 131-42+3 класса. Реферат Отчет с., 1 ч., 46 рис., 3 табл., 88 источников, 1 прил ... Если же , то координата XA определяется, как координата пересечения прямой Y = Н и прямой проведенной через точки с координатами и методом линейного интерполирования: 1.3.12,б. В этой подпрограмме организован цикл по параметру i (номеру положения входного звена механизма) от 1 до N. В зависимости от того поиск какой точки задан в блоке 3 ... |
Раздел: Рефераты по технологии Тип: реферат |