Статья: Папп Александрийский. Теоремы Паппа-Гульдена

Ткаченко А.Е., студент, Казакова Е.И., д.т.н., проф.

Донецкий национальный технический университет

В данной работе мы рассмотрим то немногое из биографии Паппа Алекасндрийского, что было нам приоткрыто из-за завесы веков и докажем одну из важнейших теорем интегрального исчисления – теорему Паппа-Гульдена.

Благодаря счастливой случайности мы узнали, когда жил Папп : 18 октября 320 н. э. он наблюдал солнечное затмение и поведал об этом в своем комментарии к «Альмагесту».

Его главным произведением является « Математическое собрание» - восьмитомное произведение. В этом сочинении Папп собрал все, что он нашел интересного в трудах своих предшественников: касательно высших кривых, о квадратуре круга, об удвоении куба и трисекции угла, методе анализа и т.д. Когда он считал необходимым что-нибудь пояснить или добавить к трудам великих геометров он излагал это в виде лемм (содержание утраченных произведений Евклида и Аполлония).

Но, кроме этого, Папп в некоторых случаях дополнил и расширил труды своих предшественников.Так, например, в своей третьей книге он дает новое построение для пяти правильных многогранников, вписанных в шар.Помимо этого она содержит историю задачи по удвоению куба и делению угла на три равные части, причем Папп привел весьма оригинальное решение первой из них. Там же Папп приводит построение треугольников и параллелограммов со сторонами большими, чем стороны данных фигур, но меньшими по площади.

Первая и вторая книги «Математического собрания» (обе утеряны) были посвящены греческой арифметике.

Четвертая книга содержит интересное обобщение теоремы Пифагора и ряд изящных предложений относительно кругов, вписанных в «арбелос» Архимеда. В той же книге Папп определяет некоторую спираль на поверхности шара и находит площадь поверхности, ограниченной этой спиралью и дугой круга (метод заимствован у Архимеда). Он показывает, каким образом, построение для neusis, примененное Архимедом в книге «О спиралях», может быть сведено к пересечению двух конических сечений.

В пятой книге излагается работа Зенодора об изопериметрических фигурах (т.е. фигурах с равными периметрами) с дополнением нескольких предложений, найденных самим Паппом .Так Папп утверждает, что из всех фигур на плоскости имеющих равные периметры, наибольшей площадью обладают фигуры с наибольшим числом углов, причем из всех фигур, наибольшее число углов вписанного многоугольника и наибольшую площадь имеет круг. В той же книге Папп отмечает, что мир по форме является шаром, «великолепнейшим» и наибольшим телом с равновеликой площадью, но философам еще не удалось доказать, что объем шара всегда больше объема любого многогранника с равновеликой площадью сторон.

В шестой книге Папп определяет центр эллипса, заданного как перспективное преобразование круга . Эта книга содержит комментарии Паппа к так называемому «Малому астроному» – сочинениям, которые читались после «Начал» Евклида и до «Альмагеста» Птоломея. Это были труды Аристарха , Автолика и «Сферика» Феодосия триполийского.

Седьмая книга имеет очень важное историческое значение, так как в ней дается обзор содержания довольно большого числа сочинений о геометрическом анализе и геометрических местах, которые почти все утеряны. Много места отведено обсуждению методов (анализу и синтезу) применявшихся древними учеными при исследованиях. В качестве собственного открытия Папп формулирует теорему относительно объемов тел вращения, которая, в сущности, есть не что иное как известная теперь «терема Паппа – Гульдена». Там же содержаться комментарии к работам Аполлония Пергского, в частности к его «Коническим сечениям».

Восьмая книга посвящена в большей своей части механике, но содержит, кроме того, и построение конического сечения, проходящего через пять данных точек . Поводом для этого послужила задача: определить диаметр цилиндрической колонны по произвольному ее обломку . Затем книга дает способ построения главных осей эллипса по двум сопряженным диаметрам.

Помимо того Папп написал и ряд других трудов, в частности, трактат «Хронография математики», в котором положил начало алгебраическим знакам, что было немаловажным достижением, если учитывать те трудности, которые возникали при письменной передаче математических достижений. К сожалению труды эти были безвозвратно утеряны.

Высокий уровень произведений обусловил интерес к их автору . Многие леммы Паппа содержат идеи уже настоящей проективной геометрии . И когда спустя много веков люди это осознали, Папп был назван последним великим геометром древности.

Но помимо достижений в геометрии Папп Александрийский достиг достаточно высокого уровня и в разработке практического применения интегрального исчисления . Одни из важнейших теорем высшей математики были сформулированы им, а через много веков над ними работал Гульден. Теперь она известны как 1-я и 2-я теоремы Паппа-Гульдена.

1-я теорема Паппа-Гульдена

Ордината центра тяжести дуги плоской кривой:

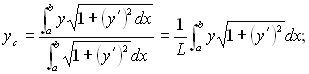
где 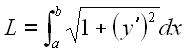- длина дуги кривой.

Преобразуем:

, (1)

Площадь поверхности тела вращения:

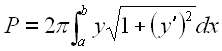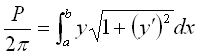или, (2)

Сравнивая уравнения (1) и (2) получаем ( если правые части уравнений равны, то равны и левые части):

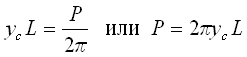, (3)

Полученное выражение (3) составляет содержание 1-й Теоремы Паппа-Гульдена:

Площадь поверхности тела вращения равна произведению длины окружности, описываемой центром тяжести кривой, на длину этой кривой.

2-я теорема Паппа-Гульдена

Ордината центра тяжести плоской фигуры:

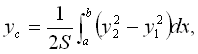
где - площадь фигуры

или

, (4)

Объем тела вращения:

или

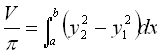, (5)

Сравнивая уравнения (4) и (5) получаем:

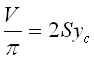
или

, (6)

Полученное выражение (6) составляет содержание 2-й Теоремы Паппа-Гульдена:

Объем тела вращения равен произведению длины окружности, описываемой центром тяжести фигуры на ее площадь.

Эти теоремы используют в инженерной практике, особенно, если кривая или фигура сложной формы. При этом центр тяжести кривой или фигуры (точнее, их моделей, выполненных из однородного материала) определяют экспериментально с помощью двух подвесов: модель подвешивают за две разные точки ее периметра и находят пересечение двух вертикальных линий, проходящих через точки подвеса. Это и есть центр тяжести. Длина дуги или площадь фигуры определяется путем взвешивания моделей и сравнивания их массы с массой эталона.

Список литературы

Ван-дер-Варден Б.Л. Пробуждающаяся наука: математика древнего Египта, Вавилона и Греции: - М.: Госиздат, 1959. – 459 с.

Крыситский В. Шеренга великих математиков: - Варшава: Наша Ксенгарня, 1981.- с.31-34.

Казакова Е.И. Интегрирование. Учебное пособие. – Донецк,: ДГТУ, 1999.-58 с.

Пак В.В., Носенко Ю.Л.Высшая математика: Учебник.-Д.:Сталкер, 2997.-560с.