Статья: Кинетика кипения воды в поле силы тяжести

Е. В. Николаева

Кипение представляет собой переход жидкости в пар, характеризующийся непрерывным образованием и ростом в жидкой фазе пузырьков насыщенного пара, внутрь которых происходит испарение жидкости [1].

Рассмотрим детально кипение воды, обратив особое внимание на роль растворенного в воде газа (воздуха) и наличие гравитации. При нагревании воды, растворенный в ней газ выделяется на дне и стенках сосуда, образуя воздушные пузырьки (ВП). В эти же пузырьки испаряется вода. Пузырек, наполненный насыщенным паром, при достаточно высокой температуре начинает раздуваться и превращается в пузырек пара (ПП). Достигнув определенных размеров, ПП отрывается от дна, поднимается к поверхности воды и лопается. При этом пар покидает жидкость. Если вода прогрета недостаточно, то ПП, поднимаясь в холодные слои, схлопывается. Возникающие при этом колебания воды приводят к появлению во всем объеме воды огромного количества мелких пузырьков воздуха: так называемый "белый ключ". Можно выделить основные стадии эволюции пузырьков при кипении:

появление и рост ВП на дне сосуда (у нагреваемой поверхности), превращение их в ПП и отрыв от дна;

подъем ПП в объеме воды и исчезновение на поверхности или в объеме;

появление ВП в объеме воды ("белый ключ") и подъем их к поверхности.

Эволюция воздушных и паровых пузырьков на дне сосуда

Рассмотрим кипение воды в плоскодонном сосуде при атмосферном давлении. Пусть дно сосуда нагревается равномерно и существует вертикальный температурный градиент. В исходном состоянии вода насыщена воздухом и имеет комнатную температуру. При нагревании воды ВП начинают появляться задолго до кипения. Они могут образовываться на дне и стенках сосуда (играя существенную роль в кипении) или в объеме при наличии полостей в воде, создаваемых внешними воздействиями.

Рис.1: Форма воздушных пузырьков, образующихся в объеме и на дне сосуда

С увеличением температуры растворимость газа в воде уменьшается [3] и воздух может выделяться в виде пузырьков при выполнении условия:

Dp і p = p0 + rв g(H - h) +2s/r, (1)

где Dp - избыточное давление растворенного газа, p - давление на поверхность пузырька, p0 - внешнее давление, rв - плотность воды, g - ускорение свободного падения, H - высота воды в сосуде, h - высота подъема пузырька, 2s/r - капиллярное давление, s - коэффициент поверхностного натяжения, r - радиус пузырька. Пузырьку легче образоваться на стенках и дне сосуда, чем в объеме, так как для равного объема (рис.1) в первом случае критическое Dp значительно меньше. На воздушный пузырек объемом V на дне сосуда действует подъемная сила:

Fпод = FA - FT = Vg(rв-rг) , (2)

где FA - сила Архимеда, FT - сила тяжести, rг - плотность газа.

Если пренебречь плотностью газа, то:

Fпод = V g rв. (3)

Пузырек прижат ко дну, поскольку на нижнюю поверхность силы давления не действуют. При малой высоте сосуда величина прижимающей силы Fпр для пузырька радиусом больше 0,1 мм определяется внешним давлением:

Fпр = p0 S = pp0 r2осн, (4)

где S - площадь соприкосновения пузырька с дном, rосн - радиус основания пузырька. Размеры пузырька определяются объемом газа, пока давление насыщенного пара в нем меньше p. При нагреве пузырек увеличивается за счет выделения в него газа и отрывается от дна, когда подъемная сила будет немного больше прижимающей [2]:

Vgrв > pp0 r2осн. (5)

Радиус пузырька, способного оторваться от дна, зависит от его формы.

Форма пузырьков

Форма пузырьков на дне определяется смачиваемостью дна сосуда [3]. При хорошей смачиваемости пузырек представляет собой усеченный шар, радиус которого много больше радиуса его несмоченного основания (рис.2).

Рис.2: Форма воздушных пузырьков на дне сосуда при различной смачиваемости

Перед тем, как оторваться от дна, пузырек поднимается на конической "ножке" (рис.3а). Поэтому толщина ножки в месте "перетяжки" (согласно нашим наблюдениям около 20 мкм), а не радиус основания определяет размеры отрывающегося пузырька. Зависимость радиуса отрывающегося пузырька от радиуса перетяжки rper:

rkp(rper) = (0.75p0/rв g)1/3 rper2/3 (6)

Диаметр всплывающих пузырьков по расчетам должен быть порядка миллиметра. Наблюдаемые размеры пузырьков были близки к расчетным. Неоднородность смачивания и слияние пузырьков на дне приводили только к увеличению их размеров.

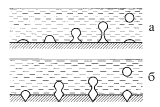
Рис.3: Эволюция пузырька пара на дне: (а) гладкое дно, (б) влияние дефектов

Пузырьки пара

Пузырьки пара образуются, когда температура придонных слоев воды достигает Tkp, при котором давление насыщенных паров в пузырьке больше p [см. (1)]. При T > Tkp пузырьки за счет пара увеличиваются в объеме в десятки раз, и отрывающиеся пузырьки можно считать состоящими только из пара. ПП, как правило, раздуваются в одних и тех же точках дна или поверхности нагревателя, связанных с дефектами (трещинками), ширина которых настолько мала, что в них не попадает вода и постоянно находится воздух (рис.3б) [2]. Эволюция ПП на дне подобна эволюции ВП, но происходит значительно быстрее и скачками.

Подъем пузырьков пара в воде

Скорость подъема оторвавшихся от дна ПП определяется их размерами, видом обтекания и вязкостью воды [2, 3]. Возможны два варианта изменения размеров ПП при всплытии:

1) если вода достаточно прогрета (T > Tkp во всем объеме), то пузырек поднимается с непрерывным увеличением размеров, достигает поверхности и лопается;

2) если T > Tkp только в придонном слое, то увеличение размеров на определенной высоте сменяется уменьшением, и пузырек схлопывается в объеме.

Подъем пузырька с увеличением радиуса

Пусть сферический пузырек поднимается под действием силы Архимеда [2]. Сила сопротивление воды при этом зависит от характера обтекания пузырька водой (рис.4).

При малых размерах наблюдается ламинарное течение: вода течет спокойно, послойно (рис.4а). Для скорости всплытия vлам выполняется формула Стокса:

vлам = Fпод/6phr = 2rвg r2 /9h, (7)

где h - коэффициент вязкости воды. Когда пузырек всплывает с постоянной скоростью, подъемная и тормозящая силы (Fпод и Fторм) равны между собой и Fторм ~ vлам. Для пузырька радиусом около миллиметра скорость всплытия vлам = 2,2 m/c и со дна стакана он должен всплыть за 0.045 c! Очевидно, что это не так. Значит для пузырьков, отрывающихся от дна, формула Стокса не применима. При больших размерах пузырька сзади него образуются пустоты, разрывы и завихрения - наблюдается турбулентное течение (рис.4б). Для такого движения можно получить приближенную формулу [2], определяющую скорость всплытия vтур:

vтур = (8rg/3)1/2. (8)

Если весь объем воды нагрет выше критической температуры, то при подъеме размеры ПП продолжают увеличиваться. Достигнув поверхности, ПП либо сразу прорывает поверхностную пленку, либо некоторое время колеблется и меняет форму, избавляясь от избыточной энергии. Когда пузырек лопается, вся окружающая его жидкость устремляется внутрь, и возникает кольцевая волна. Смыкаясь, она создает кумулятивную струю - выбрасывает вверх столбик воды, от подножья которого распространяется волна (рис.5).

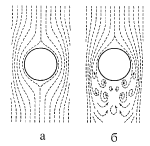
Рис.4: Ламинарное (а) и турбулентное (б) обтекание всплывающего пузырька

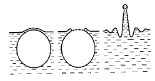
Рис.5: Разрушение пузырька пара на поверхности

Подъем пузырька с уменьшением радиуса

При вертикальном температурном градиенте и недостаточном разогреве на поверхность поднимаются только мельчайшие воздушные пузырьки. Высота подъема ПП определяется толщиной слоя, прогретого выше критической температуры, поскольку в более холодных слоях пар конденсируется. Эффект схлопывания пузырьков в объеме жидкости рассматривается при изучении явления кавитации (от латинского cavitas - пустота) - образования разрывов сплошности жидкости. При схлопывании кавитационных пузырьков в жидкости распространяются ударные волны [4] (ультразвуковых частот), сопровождаемые шумом в звуковом диапазоне. Для начальных стадий кипения характерны самые громкие и высокие звуки (на стадии "белого ключа" чайник "поет" [5]).

Для оценки характерной частоты звука [5] запишем уравнение Ньютона для массы воды m, устремляющейся внутрь пузырька при его схлопывании:

ma = SDp , (9)

где a - ускорение движения границы к центру пузырька, S = 4pr2 - площадь поверхности пузырька, Dp - разность давлений на границе пузырька. Если в процесс схлопывания вовлечена масса воды m ~ rr3, то rr3 а ~ Dp r2.

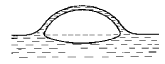
Рис. 6: Воздушный пузырек на поверхности

Будем считать Dp зависящим только от вертикального температурного градиента. Величину ускорения оценим из кинематического соотношения r = at2/2 , где t - время схлопывания пузырька: a ~ r/t2. Тогда rr2/t2 ~ Dp. Отсюда:

 (10)

Вблизи T = 100°C давление насыщенного пара уменьшается на 3·103Па при понижении температуры на градус. Поэтому можно принять Dp ~ 103Па. Время схлопывания пузырька 10-3c соответствует частоте звука 103 Гц. Колебания воды, вызванные схлопыванием пузырьков, приводят к значительному облегчению выделения растворенного воздуха в виде мельчайших пузырьков, размеры которых практически не изменяются при подъеме [2,4]. Мельчайшие пузырьки воздуха (рис.6) при достижении поверхности воды являются более долгоживущими, чем сравнительно крупные ПП. Прикасаясь к поверхности воды, они лишь слегка деформируют ее, как бы приклеиваясь к поверхности раздела с нижней стороны. Почти полностью находясь в воде, они сохраняются сравнительно долго, а лопаясь, могут быть источником высокочастотного шума.

Измерение шумов, сопровождающих кипение

Для измерений использовался высокочувствительный микрофон с усилителем, который с помощью адаптера был подключен к персональному компьютеру IBM PC 386. Усиливались сигналы в частотном диапазоне 17-70 кГц. Микрофон подносили к поверхности воды, налитой в электрочайник мощностью 1 кВт. Проводили измерения шума при нагревании воды на разных стадиях: 1) в самом начале объемной дегазации; 2) на стадии "белого ключа"; 3) при установившемся кипении. Для каждого цикла измерений наливалась свежая холодная вода. Результаты записывались в виде текстовых файлов. После преобразования Фурье были отфильтрованы гармоники спектра, вызванные селективным усилением приемного тракта, а также сигналы, амплитуда которых не превышала уровня шумов установки. Из частотных характеристик, приведенных на рис. 7, видно, что стадия "белого ключа" сопровождается значительным возрастанием акустического шума в частотном диапазоне от 35 до 60 кГц.

Можно выделить три различных механизма возникновения шума: 1) отрыв ПП от дна; 2) схлопывание ПП в объеме; 3) схлопывание ПП и ВП на поверхности. Проведем оценку характерных частот шумов для всех этих механизмов:

1. При отрыве ПП от дна характерная частота порядка 100 Гц [5].

2. По приведенной выше оценке (10) схлопывание ПП в объеме сопровождается колебаниями воды с частотой 1 кГц.

3. Характерная частота звука, возникающего, когда пузырьки лопаются на поверхности, может быть определена из соотношения (10):

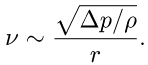 (11)

Считая, что пузырек схлопывается за счет капиллярного давления, получим:

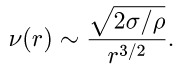 (12)

Схлопывание ПП радиусом 1-10 мм приводит к низкочастотным колебаниям порядка 100 Гц. Для ВП радиусом 40 мкм частота колебаний составляет 50 кГц.

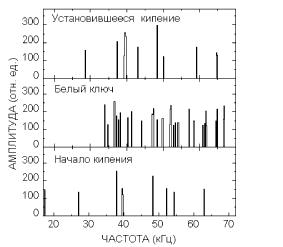
Рис. 7: Спектр шума на различных стадиях кипения

Проведенные оценки однозначно показывают, что измеренный высокочастотный шум вызван схлопыванием воздушных пузырьков на поверхности. Частотный интервал шума на стадии "белого ключа" показывает, что при индуцированной дегазации в объеме образуются воздушные пузырьки размерами от 35 до 50 мкм.

Заключение

Проведенные экспериментальные и теоретические исследования эволюции паровых и воздушных пузырьков в воде позволяют сделать следующие выводы:

1. Проведенные наблюдения за появлением и ростом пузырьков на дне и расчеты показали, что критический радиус при отрыве от дна определяется диаметром "перетяжки" и при нормальных условиях не может быть менее миллиметра.

2. Показано, что подъем пузырьков, оторвавшихся от дна, определяется турбулентным обтеканием, а пузырьков, образующихся в объеме, - ламинарным.

3. Измерение спектрального состава шумов, сопровождающих различные стадии кипения, показало, что шумы на стадии "белого ключа" связаны с образованием в объеме воздушных пузырьков размерами 35-50 мкм.

В заключение благодарю моего научного руководителя, доктора физико-математических наук, профессора Уральского государственного университета Шура Владимира Яковлевича за те исключительно увлекательные часы совместной работы, за то что сумел заинтересовать, вдохновить, и многому научить как в подходе к решению поставленной задачи, так и в оформлении результатов.

Список литературы

Кикоин И.К., Кикоин А. К. Молекулярная физика. - М., Физматгиз, 1963.

Гегузин Я. Е. Пузыри. - М., Наука, 1985.

Ландсберг Г. С. Элементарный учебник физики, Т.1, - М., Наука, 1972.

Майер В. В. Кумулятивный эффект в простых опытах. - М., Наука, 1989.

Варламов А. А., Шапиро А. И. Пока чайник не закипел . Квант. 1987. N 8.