Статья: Гравитационное поле плоского слоя

В. В. Орлёнок, доктор геолого-минералогических наук

Рассмотрим очень важную задачу притяжения, создаваемого плоским слоем в точке А, расположенной на некоторой высоте z над ним. Пусть плотность слоя r = const. Вырежем в нем диск радиусом r и толщиной Dz. Найдем потенциал элемента массы dm этого диска VА и притяжения Dg, которое он создает в точке А:

; ;

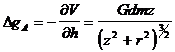,     (V.27)

где , т.е.

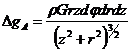.             (V.28)

Для определения притяжения всей массой диска нужно полученное выражение для элемента массы dm (V.28) проинтегрировать по всему объему диска:

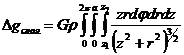.     (V.29)

Возьмем интегралы по отдельности:

;

;

.

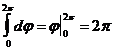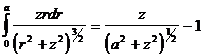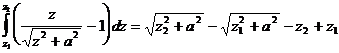Отсюда Dgслоя будет равно:

.   (V.30)

Представим

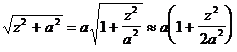.   (V.31)

Подставим (V.31) в (V.30):

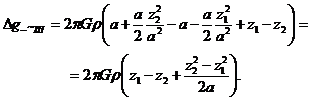   (V.32)

Проанализируем полученное выражение.

1) Если слой имеет бесконечно большие размеры в сравнении с расстоянием z до точки А, то , тогда

,    (V.33)

где  – толщина слоя.

2) Если точка А лежит на слое, т.е. z1 = 0, z2 = H, тогда

,

или

.   (V.34)

Это уже известная нам редукция Буге. Следовательно, притяжение плоского слоя не зависит от высоты наблюдения z, а зависит от толщины слоя H.