| Каталог статей | ||||||||||||||
|
Дмитренко И.С.
Сведение задачи планирования работы предприятия к задаче нелинейного программированияМатематические методы, применяемые в экономике, имеют широкий спектр направлений. В настоящее время встречаются довольно сложные модели, все более точно моделирующие реальные экономические процессы. Целью данной работы является не построение сложной экономико-математической модели, а создание реально решаемых при помощи не сложных алгоритмов, но достаточно точно приближающих, экономических моделей, которые могли бы быть с успехом внедрены в учебный процесс высшей школы. Данные модели естественно вводить в образовательный процесс как часть курса нелинейного программирования, следующего за традиционным линейным программированием. Нелинейное программирование включает в себя достаточно большой набор направлений современного исследования операций, одной из ветвей которого является сепарабельное программирование. Рассмотрим модель сепарабельного программирования, подразумевающую решение графическими методами с элементами аналитических расчетов. Модель взята из [1], с некоторыми дополнениями и усовершенствованиями. Рассмотрим задачу планирования работы некоторого условного предприятия, выпускающего продукцию двух видов A и В. Трудоемкость обработки каждого изделия на соответствующей машине, а также полезный фонд времени работы записаны в табл. 1 Таблица 1
Доход от реализации единицы продукта A составляет 0,5 ден.ед., единицы продукта B – 0,4 ден.ед. Необходимо разработать план работы предприятия на неделю, позволяющий максимизировать доход на имеющихся мощностях. Обозначим, через По таблице 1 можно построить следующую систему ограничений:
Суммарный доход, описывающий целевую функцию решаемой задачи, линейно зависит от количества единиц произведенной продукции и записывается в виде:
Воспользуемся графическим методом решения задачи (рис.1).
Область поиска экстремума ограничена
координатными осями В описанной нами ситуации величина дохода
от единицы произведенной продукции являлась константой, а это предполагает, что
вне зависимости от объема производства вся продукция находит потребителя. На
самом деле, по мере освоения технологии производства продукции, затраты
уменьшаются, спрос на нее уменьшается с увеличением числа произведенных
продуктов, т.е величина дохода является не константой, а переменной функцией.
Пусть, например, доход, получаемый от единицы продукции А, уменьшается с увеличением числа произведенных продуктов по
закону
при тех же ограничениях на область поиска переменных (рис.2).
Данная задача относится к задаче
нелинейного программирования, т.к. переменные Максимальное значение функции В случае одновременного уменьшения дохода предприятия с ростом производства по выпуску обоих видов продукции А и В, целевая функций задачи приобретает вид: или в преобразованном виде:
т.е целевая функция – окружность с центром в точке М(1000, 800). Решая задачу, аналитически найдем, что
оптимум – точка, совпадающая центром
окружности (***), т.е. линии уровня данной целевой функции представляют собой
концентрические окружности с постоянным центром и меняющимися радиусами. В
данном случае, максимальное значение функции Примененный метод решения носит название графоаналитического метода и является эффективным в случае двух переменных. Очевидно, что построенная в работе, модель является наиболее адаптированной к применению на практических занятиях по исследованию операций в высшей школе как наглядная, не трудоемкая и имеющая характерную экономическую специфику. Тем не менее, стоит отметить также тот факт, что решение подобных математических моделей является хорошей тренировкой для будущих специалистов, т.к. на практике такие задачи характеризуются, как правило, большой размерностью. Решение подобных задач можно, в дальнейшем совершенствовании модели, разбивать на соответствующие этапы, включающие в себя, соответственно, по две переменные. Литература:
| ||||||||||||||
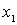 искомый выпуск за
неделю продукта A
искомый выпуск за
неделю продукта A 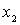 - соответственно продукта В.
- соответственно продукта В.
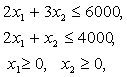

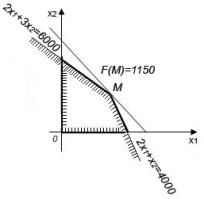 Рис.1.
Рис.1.
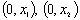 и прямыми
и прямыми 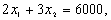
 Наибольшее значение
целевой функции
Наибольшее значение
целевой функции 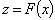 достигается в точке
достигается в точке 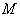 , где
, где 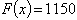 грн и соответствует выпуску
продукции А в количестве 1500 единиц,
В – 1000 единиц за неделю.
грн и соответствует выпуску
продукции А в количестве 1500 единиц,
В – 1000 единиц за неделю.
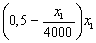 , а от продукции B – по-прежнему 0,4 ден.ед. на единицу. Тогда целевая
функция принимает вид:
, а от продукции B – по-прежнему 0,4 ден.ед. на единицу. Тогда целевая
функция принимает вид:
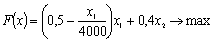 (*)
(*)
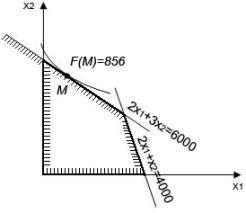 Рис.2
Рис.2
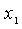 и
и 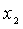 входят в целевую
функцию в степенях выше первой.
входят в целевую
функцию в степенях выше первой.
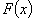 достигается в точке
достигается в точке 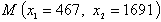 и равно 856 грн. Это
решение было найдено аналитическим путем: оптимум – точка касания прямой
и равно 856 грн. Это
решение было найдено аналитическим путем: оптимум – точка касания прямой 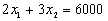 с параболой (*). Отметим, что условием задачи, естественно,
варьировать, и предполагать изменение дохода по выпуску одного лишь второго
вида продукции – В. В этом случае целевая функция задачи будет иметь, например,
такой вид:
с параболой (*). Отметим, что условием задачи, естественно,
варьировать, и предполагать изменение дохода по выпуску одного лишь второго
вида продукции – В. В этом случае целевая функция задачи будет иметь, например,
такой вид: 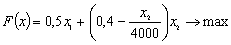 (**)
(**)
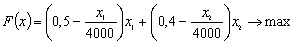 (***)
(***)
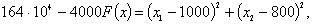
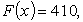 достигается в точке
достигается в точке 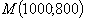 и соответствует
выпуску
и соответствует
выпуску 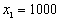 единиц продукции А и
единиц продукции А и 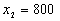 единиц продукции В за
неделю работы предприятия.
единиц продукции В за
неделю работы предприятия.