| Каталог статей |
|
Щетинина
Е.К., Падова И.Г.
Проблемы оценивания параметров распределения в задачах надежностиВ настоящее время внимание многих авторов сконцентрировано на особенностях и проблемах статистического анализа в задачах надежности. Это в первую очередь касается оценки степени изученности вопросов применения критериев согласия (при проверке сложных гипотез и цензурировании данных), предложения резко ограничить число моделей законов распределения, используемых в задачах надежности, возможности различения законов распределения при цензурированных наблюдениях. Целью работы
является рассмотрение в связи с этим известных статистик Весьма удобным для применения на практике является
замечательный вариант критерия типа Целый ряд факторов, определяющих “сложность” гипотезы, влияет на законы распределения статистик:
Математическая модель должна быть адекватной конкретной задаче исследования надежности, а используемые математические методы должны быть корректны по отношению к виду математической модели. Специфика задач надежности должна учитываться математической моделью. Методы статистического анализа определяются математической моделью, структурой наблюдений, априорной информацией и достигнутым уровнем развития математического аппарата. После предположения о характере вероятностной модели на основе имеющихся наблюдений решают два вида задач статистического анализа: 1) стараются оценить параметры этой модели таким образом, чтобы она с наибольшей точностью описывала соответствующее явление. 2) с использованием некоторого критерия проверяют адекватность модели данному явлению. Если эта модель представляет собой закон распределения, то проверка осуществляется с использованием некоторого критерия согласия. На этапе такой проверки с минимальными вероятностями ошибок гипотеза об адекватности модели должна быть принята, если это действительно так, или отклонена в пользу другой модели, более подходящей. Возможно с позиций реальных сроков жизни невосстанавливаемых изделий поздние отказы за пределами обычных сроков эксплуатации, вызываемые какими-либо процессами деградации, имеют достаточно малый вес в общем количестве отказов. Но если рассматривать моменты отказов как случайную величину, то модель закона распределения, если мы ее используем, должна адекватно описывать эти отказы на всей области определения. Простые модели, наиболее часто
используемые в задачах надежности (распределения экспоненциальное, Вейбулла,
логарифмически нормальное, гамма–распределение), не могут описать отказы,
которые определяются другими технологическими факторами. В таких ситуациях достаточно
хорошей моделью, описывающей действительность, может оказаться суперпозиция
распределений. В задачах надежности очень часто имеют дело с цензурированными
выборками. И в этом случае вследствие потерь информации из-за цензурирования
снижается качество статистических выводов: труднее идентифицировать модель,
труднее различать близкие законы распределения, снижается точность оценивания
параметров. При вычислении по цензурированным выборкам оценок максимального
правдоподобия сталкиваются со значительной смещенностью оценок, при этом
величина смещения зависит от степени цензурирования и от объема выборки. При
цензурированных наблюдениях плохо проработаны вопросы проверки сложных гипотез
о согласии эмпирического распределения с теоретическим. Конечно, при достаточно
больших объемах выборок (и достаточно большом объеме нецензурированных
наблюдений) возможно применение критериев типа Иногда невозможно различить близкие законы при цензурированных наблюдениях, но это не является серьезным основанием для отказа от применения множества моделей в пользу только одной. Поскольку при цензурировании происходят потери информации (потери информации Фишера), то это отражается на способности различать законы распределения с использованием критериев согласия и на точности оценивания параметров рассматриваемых законов. В целях наилучшего различения законов следует осуществлять проверку сложных гипотез, оценивая по выборке параметры закона, соответствующего проверяемой гипотезе. А на этом пути следует преодолеть два препятствия: ) следует на основании имеющейся информации найти по возможности наиболее точные оценки параметров; ) найти распределения статистик критериев согласия, соответствующие данному методу оценивания. Возможная точность оценок максимального правдоподобия ограничивается
снизу асимптотической дисперсией
где Возникают принципиальные сложности, связанные со смещенностью оценок параметров, вычисляемых по цензурированным выборкам. К тому же, при сильном цензурировании распределения оценок максимального правдоподобия параметров очень медленно сходятся к асимптотическому нормальному закону, а при ограниченных объемах выборок эти распределения оказываются существенно асимметричными. Однако обе эти проблемы можно преодолеть методами статистического моделирования с помощью построения для вычисляемых оценок поправок на смещение в виде функций от объема выборки и степени цензурирования. Такие поправки, нейтрализующие смещение, позволят находить несмещенные оценки параметров. А возможность построения несмещенных оценок параметров по цензурированным выборкам, позволяет исследовать распределения статистик критериев согласия, и, следовательно, корректно проверять сложные гипотезы относительно законов распределения. Построение поправок на смещение и исследование распределений статистик критериев согласия в каждом конкретном случае являются достаточно трудоемкими задачами. Поэтому выбор конкретного перечня моделей законов распределений, перспективных с точки зрения использования при исследовании надежности, для которых целесообразно построить зависимости для поправок и модели предельных распределений статистик, должен определяться специалистами, вплотную занимающимися проблемами надежности. Таким образом, в работе обозначен круг задач, обусловленных спецификой регистрации данных в задачах надежности, решение которых требует совершенствования методов статистического анализа, необходимости разработки соответствующего программного обеспечения и последующей коррекции регламентирующих документов. |
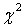 Пирсона, типа Колмогорова
и типа
Пирсона, типа Колмогорова
и типа 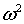 Мизеса, которые
не всегда корректно применяются при проверке сложных гипотез при решении определенных
задач надежности. Например, мощность критерия
Мизеса, которые
не всегда корректно применяются при проверке сложных гипотез при решении определенных
задач надежности. Например, мощность критерия 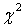 Пирсона падает
с ростом числа интервалов группирования. А при минимально возможном числе
интервалов всегда можно так осуществить группировку наблюдений, чтобы
обеспечить критерию
Пирсона падает
с ростом числа интервалов группирования. А при минимально возможном числе
интервалов всегда можно так осуществить группировку наблюдений, чтобы
обеспечить критерию 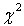 Пирсона максимальную
мощность различения близких альтернатив при проверке и простых, и сложных
гипотез. Оказывается, что при проверке простых гипотез в случае применения
асимптотически оптимального группирования критерий
Пирсона максимальную
мощность различения близких альтернатив при проверке и простых, и сложных
гипотез. Оказывается, что при проверке простых гипотез в случае применения
асимптотически оптимального группирования критерий 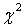 Пирсона
превосходит по мощности критерии Колмогорова, Смирнова,
Пирсона
превосходит по мощности критерии Колмогорова, Смирнова,  и
и 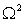 Мизеса.
Мизеса.
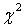 , предложенный М.С. Никулиным. И хоть статистика этого
критерия требует несколько большего объема вычислений, зато при проверке
сложных гипотез и использовании оценок максимального правдоподобия по исходным
несгруппированным наблюдениям при любом числе оцененных параметров она
подчиняется
, предложенный М.С. Никулиным. И хоть статистика этого
критерия требует несколько большего объема вычислений, зато при проверке
сложных гипотез и использовании оценок максимального правдоподобия по исходным
несгруппированным наблюдениям при любом числе оцененных параметров она
подчиняется 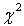 –распределению с числом степеней свободы
–распределению с числом степеней свободы  , где
, где 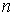 – число
интервалов группирования.
– число
интервалов группирования.
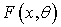 , соответствующего истинной гипотезе
, соответствующего истинной гипотезе  ;
;
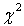 (Пирсона, Никулина). При простых гипотезах и
цензурированных наблюдениях для проверки согласия могут использоваться критерии
Реньи, которые в этой ситуации являются “свободными от распределения”. Однако,
очевидно, что при проверке сложных гипотез они теряют это свойство и,
следовательно, необходимы соответствующие исследования распределений их
статистик. В этих статистиках вполне обосновано с наибольшим весом берутся наблюдения вблизи
точек цензурирования. Применимость критериев согласия типа
(Пирсона, Никулина). При простых гипотезах и
цензурированных наблюдениях для проверки согласия могут использоваться критерии
Реньи, которые в этой ситуации являются “свободными от распределения”. Однако,
очевидно, что при проверке сложных гипотез они теряют это свойство и,
следовательно, необходимы соответствующие исследования распределений их
статистик. В этих статистиках вполне обосновано с наибольшим весом берутся наблюдения вблизи
точек цензурирования. Применимость критериев согласия типа 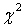 , типа
Колмогорова и типа
, типа
Колмогорова и типа 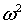 Мизеса
при цензурированных наблюдениях также требует дополнительных исследований. При
этом следует иметь в виду, что как в данном случае, так и в случае критериев
типа Реньи проверка сложных гипотез тесно взаимосвязана с проблемой оценивания
параметров.
Мизеса
при цензурированных наблюдениях также требует дополнительных исследований. При
этом следует иметь в виду, что как в данном случае, так и в случае критериев
типа Реньи проверка сложных гипотез тесно взаимосвязана с проблемой оценивания
параметров.
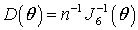 , где
, где 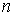 – объем выборки.
Информационное количество Фишера по цензурированной выборке определяется
соотношением
– объем выборки.
Информационное количество Фишера по цензурированной выборке определяется
соотношением
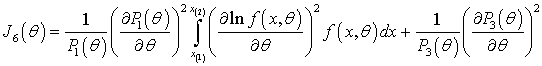 , (1)
, (1)
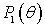 – вероятность попадания в область цензурирования
слева,
– вероятность попадания в область цензурирования
слева,  ? вероятность попадания в область цензурирования
справа, а наблюдаемая область лежит в пределах от
? вероятность попадания в область цензурирования
справа, а наблюдаемая область лежит в пределах от 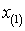 до
до 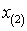 . Если выборка цензурирована только справа, то в
выражении (1) исчезает левое слагаемое, если только слева – правое слагаемое. Равенство
(1) позволяет судить о потерях информации, о параметре распределения в
зависимости от степени цензурирования слева или справа и возможной точности
оценивания. Чем больше потери информации, тем меньше возможная точность
оценивания.
. Если выборка цензурирована только справа, то в
выражении (1) исчезает левое слагаемое, если только слева – правое слагаемое. Равенство
(1) позволяет судить о потерях информации, о параметре распределения в
зависимости от степени цензурирования слева или справа и возможной точности
оценивания. Чем больше потери информации, тем меньше возможная точность
оценивания.