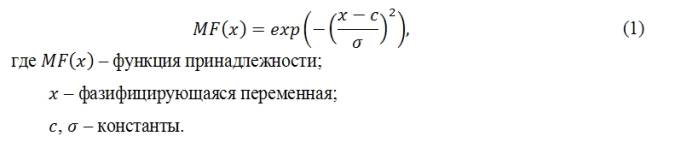| Каталог статей |
|
Глазков И.К. Южно-уральский государственный университет, Россия Применение аппарата нечёткой математики к проблеме моделирования потребности региона в рабочей силеВ условиях негативной демографической ситуации обеспечение региональной экономики рабочей силой является важной социально-экономической проблемой, затрагивающей как социальные, так и сферы экономической деятельности в Российской Федерации. Грядущие модернизационные и инновационные изменения в стране для своего осуществления требуют большого объема человеческих ресурсов. C учетом обозначенной ситуации актуальность приобретает проблема моделирования потребности региона в рабочей силе в условиях модернизационных и инновационных сдвигов в экономике. Несмотря на серьезный прорыв в исследованиях проблемы моделирования региональной потребности в рабочей силе, ее общепризнанного решения еще не найдено. С нашей точки зрения, моделирование спроса на рабочую силу в регионе обладает всеми признаками слабоструктурированной проблемы: она характеризуется высоким уровнем неопределенности, зависит от большого количества разнородных взаимодействующих факторов, часть из которых поддается воздействию лица, принимающего решения (ЛПР), а часть в принципе не зависит от него. Одним из вопросов, критичных для слабоструктурированных проблем и возникающих при моделировании спроса на рабочую силу, является учет динамично меняющейся внешней среды, испытывающей влияния модернизационных и инновационных процессов. Оба эти процесса имеют свойство оказывать достаточно существенное специфическое влияние на рынок труда, и, в частности, на такой его аспект как потребность в рабочей силе. Модернизация производства в большинстве случаев приводит к временному высвобождению рабочей силы. По мнению ряда исследователей, этот эффект может быть нивелирован так называемыми компенсационными механизмами, заключающимися в следующем:
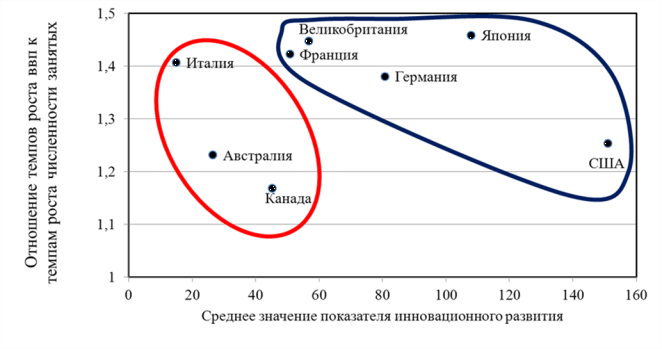
Для того, чтобы оценить влияние инновационных преобразований в экономике на потребность в рабочей силе, мы рассчитали зависимость темпов роста ВВП в расчете на одного занятого от уровня инновационного развития для ряда наиболее развитых стран за период 1975-1995 гг. (рис.1). Как видно, удалось выделить два сегмента: страны передового инновационного развития (Великобритания, Франция, Германия, Япония и США) и страны догоняющего инновационного развития (Италия, Австралия, Канада). При этом внутри каждого из выделенных сегментов прослеживается отчетливая тенденция к уменьшению отношения темпов роста ВВП к численности занятых при повышении уровня инновационного развития в стране, что в определенной степени может свидетельствовать о положительном влиянии инновационного процесса на потребность в рабочей силе.
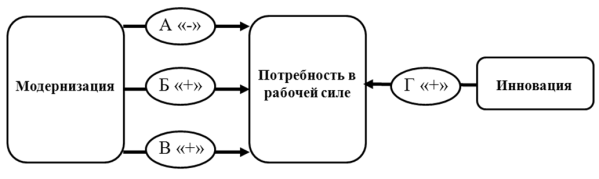
Рис. 1.Зависимость отношений темпов роста ВВП к численности занятых от уровня инновационного развития на примере ряда наиболее развитых стран Однако, несмотря на наличие обширного опыта по обновлению производственных фондов и развитию новых технологий в других странах, на настоящий момент мы не имеет четкого представления ни о том, в какой степени модернизация и инновации отражаются на региональном рынке труда, ни о характере их проекции на этот рынок. Учесть эту неопределенность при прогнозировании спроса на рабочую силу в наибольшей степени, на наш взгляд, позволяет аппарат нечёткой математики. Автором предлагается заложить в основу этого аппарата четыре лингвистические переменные, характеризующие влияние, описываемое каждой из представленных в когнитивной карте связей (рис.2):
Рис. 2. Когнитивная карта влияния модернизационных и инновационных процессов в экономике на потребность региона в рабочей силе Приведенные выше переменные характеризуются одинаковыми терм и универсальным множествами. В качестве терм множества в целях упрощения математических расчетов предлагается использовать следующее: очень низкая степень снижения/повышения потребности в рабочей силе, низкая степень, средняя, высокая, очень высокая. Границы универсального множества практически полностью зависят от внешнеэкономической обстановки и конъюнктурных особенностей изучаемого рынка, поэтому их значения определяются экспертно. Автором предлагается описать все используемые нечеткие переменные функцией принадлежности гауссова типа. Такое описание оптимально сочетает отражение реального поведения переменной и является в достаточной степени простым (1):
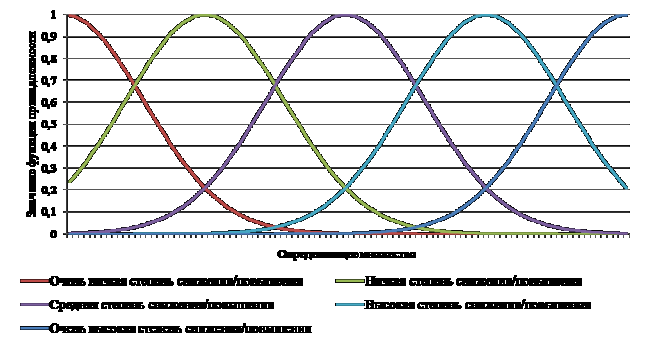
Таким образом, график каждой из используемых лингвистических переменных примет вид объединенной интегральной функции (рис 3).
Рис. 3. Функция принадлежности для степени снижения/повышения потребности в рабочей силе под влиянием различных факторов Результирующее влияние приведенных в разработанной автором когнитивной карте на потребность в рабочей силе определяется как сумма влияний каждой из четырех переменных согласно правилам операций над лингвистическими переменными, характеризующимися единым универсальным множеством. Предложенный аппарат предоставляет возможность моделировать множество ситуаций, возникающих в результате комбинации различных направлений в модернизационных и инновационных областях в единый временной период, что, в свою очередь, делает возможным проведение перспективного ситуационного анализа с целью определения наиболее выгодных комбинаций для каждого конкретного предприятия. В случае, если приведенные в когнитивной карте факторы являются в большей степени внешними и практически не подвержены влиянию непосредственно предприятия, использование предложенного аппарата предоставляет ЛПР информацию, связанную с предполагаемым изменением потребностей в рабочей силе, которую можно использовать для составления плана необходимых контрмер и его реализации. Следует отметить, что величины погрешностей при использования предложенного автором аппарата главным образом зависят от степени соответствия определяемых экспертами констант действительной рыночной ситуации. Литература
|