| Каталог статей |
|
Талайло
Е.А.
Задачи массового обслуживанияЗа последнее время в самых разных областях практики возникла необходимость в решении различных вероятностных задач, связанных с работой, так называемых систем массового обслуживания (СМО). Примерами таких систем могут служить: телефонные станции, ремонтные мастерские, билетные кассы, стоянки такси, парикмахерские и т.п. Теория массового обслуживания опирается на теорию вероятностей и математическую статистику. На первичное развитие теории массового обслуживания оказали особое влияние работы датского ученого А.К. Эрланга (1878-1929). Теория массового обслуживания - область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно, например, на предприятиях бытового обслуживания; в системах приема, переработки и передачи информации; автоматических линиях производства и др. Предметом теории массового обслуживания является установление зависимостей между характером потока заявок, числом каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Целью теории является разработка математических методов отыскания основных характеристик процессов массового обслуживания для оценки качества функционирования обслуживающей системы. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных показателей (количества каналов в системе, параметров входящего потока заявок и т.д.). Результирующими показателями или интересующими нас характеристиками СМО являются - показатели эффективности СМО, которые описывают, способна ли данная система справляться с потоком заявок. Задачи теории массового обслуживания носят оптимизационный характер и в конечном итоге включают экономический аспект по определению такого варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и простоев каналов обслуживания. В классической теории выделяют такие задачи теории массового обслуживания:
Система обслуживания считается заданной, если известны:
Каждая СМО состоит из какого-то числа обслуживающих единиц, которые называются каналами обслуживания. В качестве каналов могут фигурировать: линии связи, различные приборы, лица, выполняющие те или иные операции и т.п Всякая СМО предназначена для обслуживания какого-то потока заявок, поступающих в какие-то случайные моменты времени. Обслуживание заявок продолжается какое-то случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времен обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается излишне большое число заявок (они либо становятся в очередь, либо покидают СМО не обслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать. Рассмотрим классическую задачу теории массового
обслуживания в тех условиях, в каких она была рассмотрена и решена К.Эрлангом.
На n одинаковых приборов поступает простейший поток
требований интенсивности
где μ < 0- постоянная. Только что описанная задача представляет значительный прикладной интерес, и результаты, с которыми мы познакомимся, широко используются для практических целей. Реальных ситуаций, в которых возникают подобные вопросы, исключительно много. Использование теории систем массового обслуживания совместно с системами моделирования открывает новые возможности анализа информации и построения более точных моделей, наиболее адекватно описывающих реальные объекты окружающего мира. Литература:
|
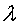 . Если в момент поступления имеется, хотя бы один свободный
прибор, оно немедленно начинает обслуживаться. Если же все приборы заняты, то
вновь прибывшее требование становится в очередь за всеми теми требованиями,
которые поступили раньше и ещё не начали обслуживаться. Освободившийся прибор
немедленно приступает к обслуживанию очередного требования, если только имеется
очередь. Каждое требование обслуживается только одним прибором, и каждый прибор
обслуживает в каждый момент времени не более одного требования. Длительность
обслуживания представляет собой случайную величину с одним и тем же
распределением вероятностей F(x). Предполагается, что при x
. Если в момент поступления имеется, хотя бы один свободный
прибор, оно немедленно начинает обслуживаться. Если же все приборы заняты, то
вновь прибывшее требование становится в очередь за всеми теми требованиями,
которые поступили раньше и ещё не начали обслуживаться. Освободившийся прибор
немедленно приступает к обслуживанию очередного требования, если только имеется
очередь. Каждое требование обслуживается только одним прибором, и каждый прибор
обслуживает в каждый момент времени не более одного требования. Длительность
обслуживания представляет собой случайную величину с одним и тем же
распределением вероятностей F(x). Предполагается, что при x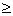 0.
0.