| Каталог статей |
|
Федотова В.И.
Хеджирование опциона американского типа с применением биномиальной модели рынкаФинансовый рынок – важная часть финансовой системы государства, неотъемлемый атрибут современной рыночной экономики. Кроме того, финансовый рынок является исключительно сложной структурой с большим количеством участников, которые вступают в экономические отношения, оперируя разнообразными финансовыми инструментами, основным классом которых являются ценные бумаги. Ценные бумаги (ЦБ) представляют собой денежные документы, подтверждающие право владения или кредитных отношений и других финансовых обязательств и определяют взаимоотношения между их эмитентом и владельцем. Особым классом современных ЦБ являются производные финансовые инструменты, или деривативы. Наиболее распространенный вид деривативов – опцион. Опцион – это контракт, дающий его покупателю право купить (опцион-колл, опцион покупателя) или продать (опцион пут, опцион продавца) определенную ценность (актив, товар и т.д.) у эмитента в установленный момент или период времени на заранее оговариваемых условиях. Держатель опциона может воспользоваться этим правом, но может и пренебречь им, если рыночная ситуация позволит ему совершить оговоренную в опционе сделку на более выгодных условиях. Стороны этого контракта неравноправны, и эмитент должен получить компенсацию, называемую премией продавцу опциона. Покупка опциона является для покупателя защитой от риска, связанного со сделкой, а премия – ценой, которую платит покупатель за эту защиту. Размер премии является основным вопросом, который возникает при продаже опциона – она должна быть достаточной для компенсации потенциальных потерь или неудобств эмитента, и такой, чтобы покупатель счел ее приемлемой платой за избавление от неопределенности. То есть премия за опцион является начальным капиталом портфеля ценных бумаг, покрывающего возможный убыток эмитента от исполнения проданного опциона. Существует много видов опционов, однако основными являются опционы европейского и американского типов. Европейский опцион может быть погашен только в одну указанную дату, американский опцион может быть погашен в любой момент времени до истечения срока опциона. То есть задача оценки стоимости опциона американского типа является более сложной, чем в случае европейского опциона, и включает в себя также задачу определения оптимального момента исполнения. Одним из самых распространенных методов оценки таких опционов является применение биномиальной модели Кокса-Росса-Рубинштейна, основанной на моделировании цены базового актива опциона (который является рисковым) с помощью дискретного случайного блуждания. Опишем соответствующую вероятностную
модель рынка для одного рискового актива. Последовательность Для оценки американского опциона в
биномиальной модели рынка используется следующая методология. Рекуррентным
образом строится стохастическая последовательность специального вида При При Для произвольного На каждом шаге в
соответствие этой функции ставится Таким образом, продолжая
указанную процедуру в обратном времени, найдем окончательное значение премии за
опцион Однако задача эмитента
заключается не только в нахождении оптимальной премии за опцион, но и в
построении такой самофинансируемой стратегии Заметим, что
Напомним, что
Проверим, что такое
распределение капитала в момент времени
т.е капитал хеджирующего портфеля
Нетрудно проверить, что
действительно Литература:
|
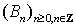 описывает
динамику цены безрискового актива (например, банковский счет); рыночные цены
рискового актива описываются стохастической последовательностью
описывает
динамику цены безрискового актива (например, банковский счет); рыночные цены
рискового актива описываются стохастической последовательностью 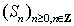 .на вероятностном пространстве рынка. Также на
указанном пространстве рассматривается фильтрация
.на вероятностном пространстве рынка. Также на
указанном пространстве рассматривается фильтрация 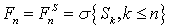 , которая интерпретируется как объем информации,
доступный каждому участнику рынка в момент
, которая интерпретируется как объем информации,
доступный каждому участнику рынка в момент 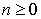 . Т.е. для любого
. Т.е. для любого 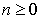 случайные
величины, измеримые относительно
случайные
величины, измеримые относительно 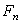 , становятся полностью известными всем участникам рынка
в момент не позже
, становятся полностью известными всем участникам рынка
в момент не позже 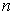 . Портфелем ЦБ
называется пара
. Портфелем ЦБ
называется пара 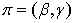 последовательностей величин
последовательностей величин 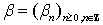 и
и 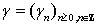 - вкладов
соответственно в безрисковый и рисковый активы в единицах этих активов. Капитал
же портфеля равен, таким образом
- вкладов
соответственно в безрисковый и рисковый активы в единицах этих активов. Капитал
же портфеля равен, таким образом 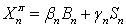 . Начальные цены рассматриваемых активов
. Начальные цены рассматриваемых активов 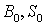 известны, кроме того,
не ограничивая общности можно считать
известны, кроме того,
не ограничивая общности можно считать 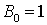 . Временной горизонт рассматриваемого американского опциона
. Временной горизонт рассматриваемого американского опциона 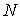 определен. Возможные
убытки эмитента и, соответственно, доходы держателя опциона в каждый момент
времени описываются неслучайной функцией цен рискового обязательства
определен. Возможные
убытки эмитента и, соответственно, доходы держателя опциона в каждый момент
времени описываются неслучайной функцией цен рискового обязательства 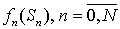 , которая называется платежным обязательством. Таким образом,
опцион американского типа порождает совокупность платежных обязательств
, которая называется платежным обязательством. Таким образом,
опцион американского типа порождает совокупность платежных обязательств 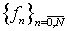 , подлежащую покрытию. Ставка изменения цены безрискового
актива за один такт времени
, подлежащую покрытию. Ставка изменения цены безрискового
актива за один такт времени 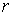 детерминирована,
ставка изменения цены рисковой ЦБ
детерминирована,
ставка изменения цены рисковой ЦБ 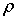 является случайной
величиной, сосредоточенной в точках
является случайной
величиной, сосредоточенной в точках 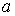 и
и 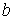 , причем
, причем 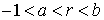 . Описанный таким образом рынок является полным , на нем
существует единственная мера
. Описанный таким образом рынок является полным , на нем
существует единственная мера 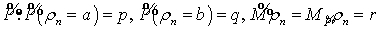 , называемая мартингальной и применяемая для оценки стоимости
платежных обязательств, порождаемых опционами.
, называемая мартингальной и применяемая для оценки стоимости
платежных обязательств, порождаемых опционами.
 :
:
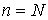
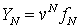 .
.
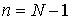 :
: 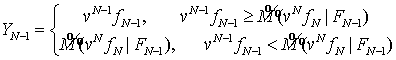 .
.
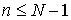
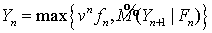 . Очевидно, что
. Очевидно, что 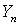 является
является 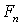 -измеримой случайной величиной.
-измеримой случайной величиной.
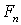 -измеримая случайная величина
-измеримая случайная величина 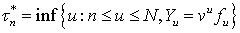 , трактуемая как момент исполнения опциона. Это выражения
следует понимать так: если в текущий момент времени дисконтированное платежное
обязательство строго меньше максимального прогноза будущего
, трактуемая как момент исполнения опциона. Это выражения
следует понимать так: если в текущий момент времени дисконтированное платежное
обязательство строго меньше максимального прогноза будущего 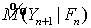 , то опцион не следует подавать к исполнению.
, то опцион не следует подавать к исполнению.
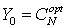 , а также искомый момент остановки
, а также искомый момент остановки 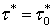 .
.
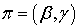 с начальным капиталом
с начальным капиталом
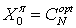 , которая покрыла бы порождаемое опционом платежное
обязательство в момент его исполнения:
, которая покрыла бы порождаемое опционом платежное
обязательство в момент его исполнения: 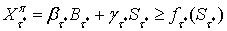 .
.
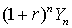 есть ни что иное, как
капитал, необходимый в момент времени
есть ни что иное, как
капитал, необходимый в момент времени 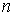 для покрытия текущего
и всех возможных будущих платежных обязательств
для покрытия текущего
и всех возможных будущих платежных обязательств 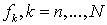 , и вычислим требуемые коэффициенты
, и вычислим требуемые коэффициенты 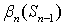 и
и 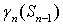 , руководствуясь принципом покрытия на следующем шаге определенного
платежного обязательства, что равносильно достижению на следующем шаге
капитала, необходимого для покрытия всех платежных обязательств
последовательности в будущем, а именно:
, руководствуясь принципом покрытия на следующем шаге определенного
платежного обязательства, что равносильно достижению на следующем шаге
капитала, необходимого для покрытия всех платежных обязательств
последовательности в будущем, а именно:
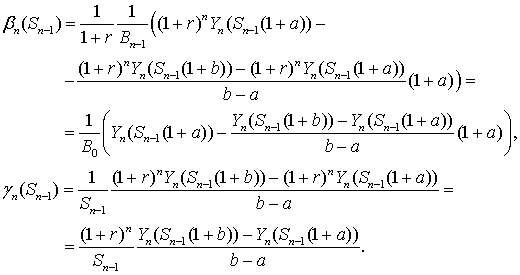
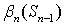 и
и 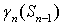 являются
являются 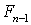 измеримыми. Общая
сумма капитала, вложенного в безрисковый актив в момент времени
измеримыми. Общая
сумма капитала, вложенного в безрисковый актив в момент времени 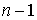 составит:
составит:
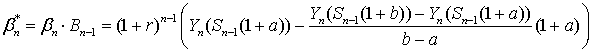 .
.
 действительно возможно.
Пусть в момент времени
действительно возможно.
Пусть в момент времени 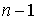 эмитент опциона
располагает капиталом
эмитент опциона
располагает капиталом 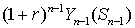 , и в этот момент опцион не исполняется. Это значит, что
, и в этот момент опцион не исполняется. Это значит, что
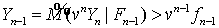 ,
,
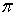 в момент времени
в момент времени 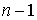 равен:
равен:
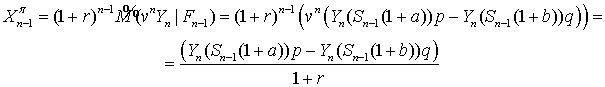 .
.
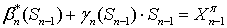 , то есть такой вклад возможен. Аналогичным образом можно
проверить, что
, то есть такой вклад возможен. Аналогичным образом можно
проверить, что 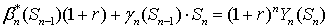 , то есть такой портфель действительно покрывает платежное
обязательство
, то есть такой портфель действительно покрывает платежное
обязательство 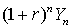 для любого
для любого 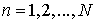 .
.