| Каталог статей | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Студент гр. МЗД 05мз Гумбатов Р.А.,
Оценка форм оплаты международных контрактовВажной сферой деятельности управленческого персонала предприятий ВЭД являются выбор предпочтительных форм расчетов по международным контрактам. В условиях, когда спрос на продукцию имеет значительный коэффициент вариации, существенное значение имеет правильный выбор форм расчетов, определяющий надежность международной сделки на заключительном этапе. Было выбрано три формы расчета ah a2 и а3.(чеки, инкассовая и аккредитивная форма расчетов), Определено шесть критериев выбора: F1 — затраты при расчетах; F2 — гарантии; F3 — сроки расчетов; F4 — валюта расчетов; F5 — штрафные санкции; F6, — сумма контракта Значения критериев для всех альтернатив определены в табл. 1. Таблица 1- Значения критериев для альтернатив
Для каждой альтернативы определены конкретные значения, которые представлены следующими нечеткими множествами: μF1 = {0,05/3.0 + 0,25/3.5 + 0,4/4.0}; μF2 = {0,7/1+ 1,0/1.5+0,3/2}; μF3= {0,35/1.5 + 0,6/2.0 + 0,2/1.0}; μF4 = {0,25/4+ 0,7/5 + 0,3/5}; μF5= {0,5/2 + 0,9/2,5 + 0,35/1,5}; μF6 = {1,0/5 + 0,75/4 + 0,6/3}. Критерии имеют различную значимость при определении наиболее рационального варианта. В связи с этим необходимо определить весовые коэффициенты βi критериев. Один из возможных способов получения значений весовых коэффициентов заключается в построении матрицы попарных сравнений критериев. Для критериев, использованных при решении задачи выбора лучшей формы расчетов, представлена следующая матрица: Таблица 2- Попарное сравнение критериев
Весовой коэффициент критерия βi, определяется на основании вычисленных значений правого собственного вектора матрицы попарных сравнений αi, с последующим умножением на число критериев n.
Значения α и β , приведены в табл. 3 Таблица 3- Собственный вектор матрицы попарных сравнений
Множество оптимальных альтернатив В с учетом различной важности критериев качества определяется путем пересечения нечетких множеств следующим образом:
Найдем множество оптимальных альтернатив с учетом полученных весовых критериев: В = { min { 0,051.062; 0,70..318; 0,350.404; 0,250..589; 0,52.652; 1,00..972 } min { 0.251.062; 1,00..318; 0,60.404; 0,70..589; 0,92.652; 0,750..972 } min { 0,41.062; 0,30..318; 0,20.404; 0,30..589; 0,352..652; 0,60..972 }}. Множество оптимальных
вариантов В имеет вид: max Таким образом, лучшей альтернативой является инкассовая форма а2, на втором месте аккредитив a3 самым худшим вариантом для расчета являются чеки a3. Функция
предпочтения При оценке предпочтений по критериям экспертами использована пяти балльная оценка. Правый собственный вектор попарных сравнений критериев (табл.2) при определении весовых коэффициентов находится в несколько этапов.
Процесс оценки форм расчетов характеризуется совокупностью частных критериев, часто находящих во взаимном противоречии друг с другом, когда улучшение по одному из показателей ведет к ухудшению по другому. Кроме того критерии и ограничения на практике часто задаются на вербальном уровне в форме нечетких утверждений весьма общего характера, что дополнительно вносит существенную неопределенность в решаемую задачу. Литература:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
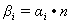
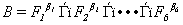 ;
;
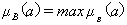 ;
;
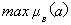 = max {0,041; 0,229; 0,062}.
= max {0,041; 0,229; 0,062}.
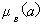 берется в диапазоне 0-1, устанавливается экспертами по
отношению к альтернативе , например , предпочтение 0.05 по отношению к первой
форме расчетов и затрат на
осуществление (0,05/30).
берется в диапазоне 0-1, устанавливается экспертами по
отношению к альтернативе , например , предпочтение 0.05 по отношению к первой
форме расчетов и затрат на
осуществление (0,05/30).