| Каталог статей |
|
Садыков
В.М., Миронцова А.С.
Теоретические аспекты динамического моделирования финансовых временных рядовНаиболее интересным приложением теории нелинейных систем является прогнозирование динамики порождаемых ими временных рядов. В последнее время все большее внимание уделяется исследованию именно финансовых временных рядов с точки зрения теории динамических систем. Это достаточно новая область, которая представляет собой популярный и активно развивающийся раздел математических методов экономики. Развитие теории в этом направлении дает возможность выявить существо глубинных экономических процессов, зачастую скрытых и неявных, и позволяет перевести субъективные и интуитивные суждения на строгий язык цифр и фактов. Анализ экономических временных рядов предоставляет возможность с определенной степенью точности заглянуть в будущее, т. е. осуществить прогнозирование развития ситуации. При этом отдельно встает вопрос о точности такого прогноза. Проблемами динамического моделирования систем занимались как отечественные, так и зарубежные ученые. Среди них Г.Г Малинецкий [1], С.П. Курдюмов [1], A.A. Бредихин [2], А.Ю. Лоскутов [2], А. Лихтенберг, М. Либерман, Д.Н. Дерюгин, А.К. Бера [3], М. Хиггинс [3], Е.А. Джексон, Ф. Такенс, A. Винфри, А. Гальчинский, Г. И. Башнянин и др. Целью данной работы является рассмотрение теоретических аспектов наиболее эффективных подходов к решению проблемы динамического моделирования временных рядов, в том числе и финансовых. Временной ряд – это функция от времени, по которой судят о процессе в исследуемой системе. Большинство систем в силу их сложности, не могут быть смоделированы с достаточной точностью. Однако их описание может быть выполнено посредством иного подхода, основанного на наблюдении за их поведением [2]. Если временной ряд определенным образом обработать, то при некоторых условиях возможно с большой точностью произвести оценку будущего значения этого ряда, причем эта оценка представляет собой функцию только от предыдущих значений ряда. Следовательно, на основе одних лишь наблюдений за системой, возможно предсказать ее поведение в будущем. При каких условиях могут быть динамически смоделированы некоторые временные ряды и успешно осуществлено их прогнозирование? Для ответа на этот вопрос проследим за изменением временного ряда. В результате получим некоторую функцию. Если измерения производились в фиксированные моменты времени, то эта функция примет дискретный ряд значений. Если исследуемая система - динамическая, т. е. описывается конечным набором обыкновенных дифференциальных уравнений, то временной ряд всегда будет функцией от его фазовой точки. Однако, как правило, заранее неизвестно, возможно ли описать данный процесс динамически. Тем не менее, в рамках современной теории размерности и теории динамических систем можно, в принципе, отличить шум (случайный процесс) от детерминированного поведения и тем самым установить конечномерность рассматриваемого явления. Финансовый временной ряд - это
последовательность, описывающая поведение определенного рыночного процесса [2].
В ряде работ был проведен анализ некоторых финансовых рядов и показано, что
многие из них имеют конечную емкость. Таким образом, эти ряды могут быть описаны
обыкновенным дифференциальным уравнением конечного порядка (Например, Для решения этой проблемы можно предложить два наиболее эффективных недавно разработанных подхода. Первый подход связан с использованием данных о процессе формирования цен финансовых активов. Эти данные, в основном, сконцентрированы в самостоятельном разделе экономической теории, называемом теорией финансов. Использование моделей этой теории может оказаться полезным при определении вида уравнений с точностью до конечного числа параметров. В свою очередь, определение параметров может быть произведено на основании оптимального приближения решения этих уравнений к имеющимся данным. При этом получается, что длина временных рядов, необходимая для определения параметров, может быть на порядки меньше, чем для решения исходной непараметрической задачи. Эмпирические наблюдения за финансовыми временными рядами позволяют подметить следующие особенности:
Интерпретация этих особенностей с точки зрения теории динамических систем составляет суть второго подхода [1]. Развитие этих подходов показывает принципиальную возможность провести реконструкцию правой части дифференциального уравнения на основе общих соображений без использования длинных рядов наблюдений. Однако для их разработки используются достаточно жесткие предпосылки. Тем не менее, ряд обобщений, используемых в нелинейной динамике, позволяет перейти к практическому прогнозированию на финансовых рынках, причем в некоторых случаях такое прогнозирование может быть достаточно просто реализовано. В работе представлены лишь два (достаточно эффективных) подхода. Однако, естественно, решение проблемы описания финансовых рядов ими не исчерпывается. Среди зарубежных исследователей весьма популярным подходом для анализа финансовых временных рядов является идея использования концепции так называемой авторегрессионной условной гетероскедастичности (ARCH, авторегрессионность – зависимость от предшествующих значений ряда, условность – дисперсия рассчитывается при условии, что предшествующие значения ряда известны, гетероскедастичность – изменение дисперсии во времени) [3]. Она состоит в том, что изменение дисперсии определяется не внешними факторами, а внутренними параметрами и предысторией системы, в частности, реализованными в предыдущие моменты времени значениями временного ряда. Таким образом, становится возможным не только описывать поведение исследуемого временного ряда, но и прогнозировать его динамику. Теоретические исследования, основанные на анализе временных рядов, в том числе и финансовых, могут дать мощный инструмент для моделирования многих явлений, особенно когда имеющихся данных недостаточно для построения модели другим способом. Литература:
|
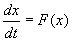). При некоторых условиях это уравнение дает возможность
прогнозировать динамику временного ряда, однако для этого сначала нужно
восстановить его правую часть. В некоторых работах проводились оценки длины
временного ряда, необходимой для такого восстановления. Эти оценки показывают,
что в большинстве случаев имеющихся данных недостаточно для определения правой
части уравнения.