| Эконометрика (Яковлева А.В.) |
Нормальная линейная модель парной (однофакторной) регрессииОбщий вид нормальной (традиционной или классической) линейной модели парной (однофакторной) регрессии (Classical Normal Regression Model): yi=0+1xi+i, где yi– результативные переменные, i=1,n; xi – факторные переменные, i=1,n; 0, 1 – параметры модели регрессии, подлежащие оцениванию;
При построении нормальной линейной модели парной регрессии учитываются пять условий: 1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии i; 2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю): Cov(i,j)=E(i,j)=0 (). Это условие выполняется в том случае, если исходные данные не являются временными рядами; 5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: i~N(0, G2). Общий вид нормальной линейной модели парной регрессии в матричной форме: Y= X* + , где
Условия построения нормальной линейной модели парной регрессии, записанные в матричной форме: 1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии i;
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях; 3) третье и четвёртое условия можно записать через
ковариационную матрицы случайных ошибок нормальной линейной модели
парной регрессии:
где G2 – дисперсия случайной ошибки модели регрессии ; In – единичная матрица размерности n x n. Определение. Ковариацией называется показатель тесноты связи между переменными х и у, который рассчитывается по формуле:
где
Основными свойствами показателя ковариации являются: а) ковариация переменной и константы равна нулю, т. е. cov(x,C)=0 (C=const);
4) случайная ошибка модели регрессии подчиняется нормальному закону распределения: i~N(0, G2). Яковлева А.В. Эконометрика |
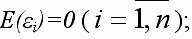
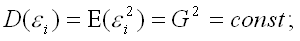
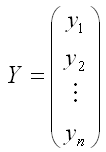 – случайный вектор-столбец значений результативной переменной размерности n x 1;
– случайный вектор-столбец значений результативной переменной размерности n x 1;
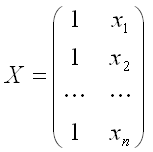 – матрица значений факторной переменной размерности n x 2. Первый столбец является единичным, потому что в модели регрессии коэффициент 0 умножается на единицу;
– матрица значений факторной переменной размерности n x 2. Первый столбец является единичным, потому что в модели регрессии коэффициент 0 умножается на единицу;
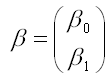 – вектор-столбец неизвестных коэффициентов модели регрессии размерности 2 x 1;
– вектор-столбец неизвестных коэффициентов модели регрессии размерности 2 x 1;
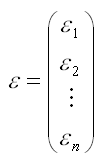 – случайный вектор-столбец ошибок модели регрессии размерности n x 1.
– случайный вектор-столбец ошибок модели регрессии размерности n x 1.
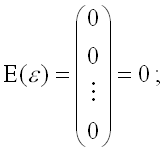
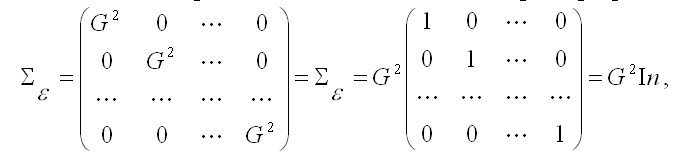
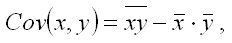
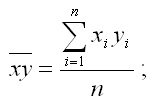 – среднее арифметическое значение произведения факторного и результативного признаков;
– среднее арифметическое значение произведения факторного и результативного признаков;