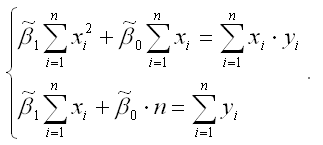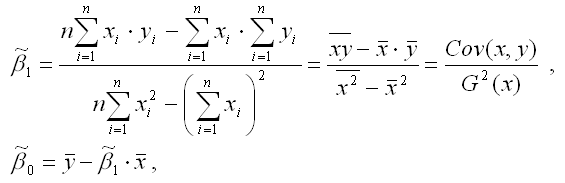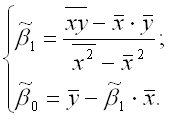| Эконометрика (Яковлева А.В.) |
Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратовПредположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:
В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Метод наименьших квадратов позволяет получить такие оценки параметров 0 и 1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) минимальна:
В процессе минимизации функции (1) неизвестными являются только значения коэффициентов 0 и 1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=0+1xi:
Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии 0 и 1:
где y – среднее значение зависимой переменной; x – среднее значение независимой переменной; xy – среднее арифметическое значение произведения зависимой и независимой переменных; G2 (x) – дисперсия независимой переменной; Gcov (x, y) – ковариация между зависимой и независимой переменными. Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:
Яковлева А.В. Эконометрика |
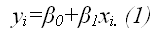

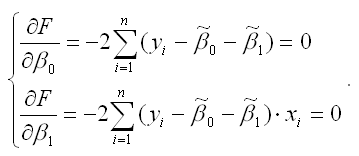 .
.