Каталог статей

Асканбаева Г.Б.

Векторный метод при решении олимпиадных задач

Решение задач служит одним из средств овладения системой научных знаний по тому или иному учебному предмету. Особо велико значение решения задач в овладении системой понятий.

Неоценима роль процесса решения задач в овладении умениями и навыками познавательного и практического характера. Развитие творческого мышления, самостоятельности, подготовка студентов к творческому труду возможны только при условии систематического решения задач.

Задача считается нестандартной, если для ее решения требуется применить нестандартные методы решения. Такие виды задач в основном представляются для решения в математических олимпиадах, которые очень часто проводятся как среди школьников, так и среди студентов. Поиск решения нестандартных задач развивает инициативу, настойчивость и сообразительность. Главное в решении задач олимпиадного уровня - логическая основа, поэтому решение должно быть логически полным рассуждением, не содержащим ошибок.

Основная задача олимпиадного движения – пропаганда математических знаний среди молодежи, подготовка к будущей научной деятельности, заострение интеллекта. Чтобы студенты увлекались решением математических задач, необходимо их заинтересовать, а это сделать достаточно нелегко. Но если задача увлекательна, то интерес к ней, независимо от желания студента, мобилизует его умственную энергию, облегчает запоминание. Когда студент работает над теоретическим материалом, то усваивает чужие мысли, когда решает задачи, то мыслит самостоятельно. Польза от решения заключается не в отыскании ответа, а в том, что в процессе решения студент целенаправленно, последовательно совершенствует технику (закрепляет знание формул, алгоритмов, методов и приемов решений), развивает творческие способности. Элементы творчества на начальном этапе размышления над задачей переходят в технику решения на завершающем этапе[2]. Студентам специальности «Математика» в курсе изучения дисциплины «Практикум по решению математических задач» предлагаются решать задачи повышенной трудности, а также олимпиадные задачи. Покажем, как теоретический материал по применению векторного метода используется при решений олимпиадных задач.

Понятие вектора является одним из фундаментальных понятий современной математики. С помощью векторов могут быть решены содержательные геометрические задачи, причем их векторные решения часто значительно проще и эффективнее решений средствами элементарной геометрии. При решении задач находят применение сведения, известные из школьного курса геометрии: действие сложения векторов и его законы, вычитание векторов, действие умножения вектора на число и его законы, понятие коллинеарности векторов, разложение вектора в данном базисе, единственность разложения. Посредством этих действий и их свойств можно решать задачи на параллельность прямых, принадлежность трех точек одной прямой, вычисление отрезков параллельных прямых и некоторые другие. Однако задачи на вычисление расстояний и углов с помощью этих действий не могут быть решены. Для решения задач, связанных с длинами и углами (их называют метрическими), применяется скалярное умножение векторов и его свойства. Умение пользоваться векторным методом требует определенных навыков. Прежде всего необходимо хорошее знание теории. Надо научиться переводить геометрические соотношения между фигурами на векторный язык, а также, наоборот, полученные векторные соотношения истолковывать геометрически. Полезно запоминать некоторые, часто встречающиеся при решении задач векторные соотношения и обратить внимание на их большую общность.

Основные формулы и соотношения, используемые при решении задач.

1) Правило сложения векторов:.

2) Правило вычитания векторов: , где О — произвольная точка.

3) Условие принадлежности трех точек А, В и С одной прямой:

a); б), где k — некоторое число.

4) Условие параллельности отрезков АВ и CD:.

5) Формула деления отрезка в данном отношении:

если , то , где О — произвольная точка.

6) Формула середины отрезка: если С — середина отрезка АВ, то .

При решении задач часто находит применение следующее свойство векторов:

7) Единственность разложения вектора по двум неколлинеарным векторам: если векторы и неколлинеарны, то из равенства следует, что х = х₁ и у= у₁

8) Если М и N — середины сторон АВ и CD четырехугольника ABCD, то .

9) Четырехугольник ABCD является параллелограммом тогда и только тогда, когда выполняется одно из соотношений:

а) ; 6) ; в)

10) Если ABCD — трапеция с основанием АВ, стороны АО и ВС которой при продолжении пересекаются в точке Р, а диагонали – в точке О. то , и ,, где .

Особенностью векторных решений многих задач является то, что все привлекаемые для решения векторы откладываются от одной точки, удачный выбор которой часто позволяет упростить вычисления.

Многие геометрические задачи на вычисление расстояний и углов, на доказательство геометрических тождеств и неравенств могут быть решены при помощи скалярного произведения векторов.

По определению скалярного произведения векторов , следовательно,

Равенство применяется для нахождения длины вектора.

Кроме этих формул и соотношений, для решения метрических задач используются также следующие:

11) Для ненулевых векторов и :из следует, что

12) Для любых векторов и :

13) Для любых векторов и :

14) Для любых трех векторов , и :

15) Для любых трех векторов , и :

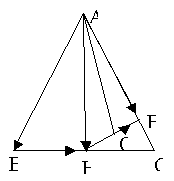
16) Для любых трех точек A, В и С: Это равенство равносильно теореме косинусов.

17) Для любых четырех точек А, В, С и D:

[1].

Приведем пример использования векторного метода для решения задачи, которую можно решить и другими методами.

Пример.

Из середины H основания BC равнобедренного треугольника ABC проведен перпендикуляр HE на сторону AC. Точка O – середина HE. Докажите, что отрезки BE и AO перпендикулярны.

Решение:

Чтобы доказать перпендикулярность отрезков ВЕ и ОА, надо показать что скалярное произведение этих векторов равно нулю, т.е. ·=0.