Катаргин Н.В., к.т.н. Богомолов А.И., к.т.н. Костюнин В.И.

Исследование системы, состоящей из производителей продукции, власти и криминала

где N – население

      Y – произведённая продукция

      a, b, c, A  – коэффициенты.

         Нами проведено исследование данной системы уравнений методом конечных разностей в среде Excel. Начальное население N = 100, временной интервал dt = 0,01.  Далее приведён пример: часть таблицы Excel с формулами и результатами расчетов.

                                                                                      Таблица 1.

	А	В	С
1	N	dN	Y
2	100		=A*A2^c
3	=А2+В3	=(a*A2-b*A2^2/C2)*dt	22,257
4	71,967	-12,165	19,952
5	62,432	-9,534	18,062
6	54,818	-7,613	16,491

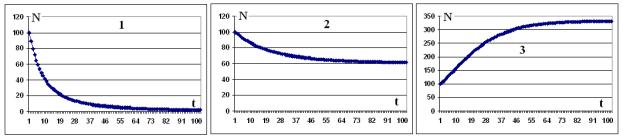
         Некоторые результаты расчётов представлены в Таблице 2 и на Рисунке 1. Изменённые коэффициенты очерчены рамками. Номера графиков на Рисунке 1 соответствуют номерам колонок в Таблице 2.

Таблица 2.

№	1	2	3	4	5	6	7	8	9
a	3	12	20	20	30	50	50	50	50
b	7	7	7	7	7	7	7	7	5
c	0,7	0,7	0,7	0,7	0,7	0,7	0,6	0,5	0,5
A	2	2	2	1	1	1	1	1	1
Асимптота	0,6	60,8	333,6	33,1	128	702	136	51	100

Рис. 1. Динамика популяции в зависимости от параметров системы.

На графиках видно, что решения системы уравнений близки к экспонентам, стремящимся к асимптотам, которые, как показали расчеты,  не зависят от начального значения N.

         Мы также исследовали расширенную модель Хаавельмо, включив в неё действующих лиц: криминал ( К ) и власть ( V ). Криминал забирает себе часть продукции Y, равную  rK, размножается со скоростью fK и при дефиците продукции вымирает со скоростью sK²/Y, т.е. по тому же закону, что и население. Власть уменьшает количество криминала с эффективностью е, т.е. на eV за временной интервал. Власть (точнее, расходы на власть) пропорциональна продукции ( = vY ) и уменьшает Y на величину V. Модель принимает вид:        

                                           V = vY

Во всех расчетах использованы коэффициенты столбца 6 первой модели и одинаковые коэффициенты: размножения криминала f, убывания криминала s и пропорциональности продукции и власти v:

a	b	c	А	f	s	v
50	7	0,7	1	20	7	0,1

Фрагмент таблицы Excel для расчётов представлен в Таблице 3, результаты расчётов – в Таблице 4 и на Рисунке 2.

                                                                                          Таблица 3.

	A	B	C	D	E
3	N	dN	Y	K	V
4	100		24,51	3	2,45
5	121,45	21,45	25,68	3,19	2,56
6	141,98	20,53	28,85	3,39	2,88

                                                                                                 Таблица 4.

№	6 табл.2	1	2	3	4	5	6
r	0	0,2	0,33	0,2	0,2	0,2	0,1
e	0	2	2	12	15,6705	15,67051	2
Асимптота населения	702	127	65	130	131	511	237
Асимптота криминала	0	50,7	26	51	51	0	94,5

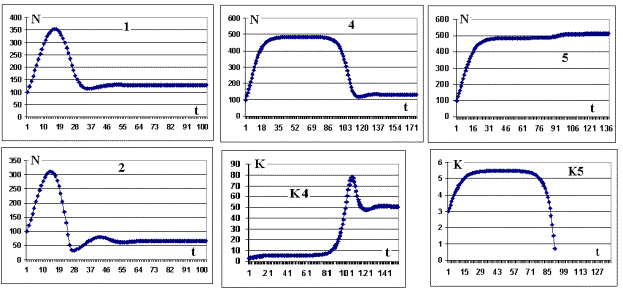
Рис. 1. Динамика популяции  и криминала в зависимости от параметров системы.

Рассмотрение Таблицы 4 и Рисунка 2, а также эксперименты с начальными значениями N и K приводят к следующим выводам:

1. Население и криминал могут испытывать значительные  колебания в начальной стадии процесса, но в конечном итоге стремятся к асимптотам, если не произошла катастрофа. Изменение начальных значений N и K не приводит к существенному изменению  асимптот.

2. Криминал, присваивающий даже небольшую часть продукции, в перспективе резко сокращает население и производство: при r =10%  асимптота населения падает в 3 раза ( сравните № 6 таблиц 1 и 4 ), при     r = 20% в 5 раз ( № 1 ). При r = 33%  имеют место затухающие колебания населения и криминала, асимптота падает в 10 раз ( № 2 ); около 40% наступает катастрофа: население  падает до нуля.

3. Эффективность власти е не влияет на асимптоты криминала и незначительно (до 15%) влияет на асимптоту населения, однако существуют критические значения коэффициентов e, при которых  действия власти могут поддерживать количество населения довольно длительное время на высоком уровне   ( № 4 ), но, в конечном итоге, криминал начинает быстро расти, затем и криминал, и население  падают и стабилизируются ( Рис.2,  графики 4, К4 ). Критические значения е пропорциональны начальному значению криминала К (расчёты проведены при К₀ = 3, а при К₀  = 20 е_крит.= 92,5 ). При ничтожном превышении критического значения е (сравните № 4 и      № 5) криминал через какое-то время полностью истребляется,  население и производство стабилизируются на существенно более высоком уровне (Рис.2, № 5 и К5).