| Эконометрика (Яковлева А.В.) |
Состоятельность и несмещённость МНК-оценокПредположим, что методом наименьших квадратов получена оценка
Для того, чтобы данная оценка могла быть принята за оценку параметра
Сделаем следующие предположения об отклонениях єi:
Если данные предпосылки выполняются, то оценки, найденные с помощью метода наименьших квадратов, обладают свойствами несмещённости, состоятельности и эффективности. Если третье и четвёртое предположения не выполняются, т. е. дисперсия случайных компонент непостоянна и/или значения є коррелируют друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности – нет. Величина
Отсюда следует, что
где i – это величина смещения оценки. Рассмотрим свойство несмещённости МНК-оценок на примере модели парной регрессии. Необходимо доказать, что оценка
Доказательство. Проведём доказательство утверждения
через ковариационную матрицу:
То же самое утверждение
можно доказать в более развёрнутом виде:
Следовательно, оценка Свойство несмещённости оценки Для модели множественной регрессии доказательство свойства несмещённости оценок параметров i, полученных методом наименьших квадратов, целесообразно провести в матричной форме:
Следовательно, оценки Величина
Условие состоятельности можно также записать через теорему Бернулли:
т. е. значение оценки
На практике оценка
1) смещение оценки равно нулю или стремится к нему при объёме выборки, стремящемся к бесконечности:
2) дисперсия оценки параметра
Рассмотрим свойство состоятельности МНК-оценок на примере модели парной регрессии. Необходимо доказать, что оценка
Доказательство. Докажем первое условие состоятельности для МНК-оценки
Докажем второе условие состоятельности для МНК-оценки
МНК-оценка
или
где индекс 22 указывает на расположение дисперсии параметра 1в матрице ковариаций. Свойство состоятельности оценки
Оценка стандартной ошибки МНК-оценки
Для модели множественной регрессии доказательство свойства несмещённости оценок параметров i, полученных методом наименьших квадратов, целесообразно провести в матричной форме:
Следовательно, оценки
Эффективность МНК-оценок доказывается с помощью теоремы Гаусса-Маркова. Яковлева А.В. Эконометрика |
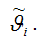
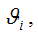 необходимо и достаточно выполнения трёх статистических свойств:
необходимо и достаточно выполнения трёх статистических свойств:
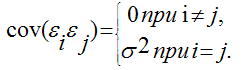
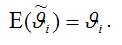
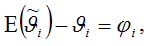
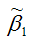 полученная методом наименьших квадратов, является несмещённой оценкой параметра 1 для нормальной линейной модели регрессии, т. е. необходимо доказать справедливость равенства
полученная методом наименьших квадратов, является несмещённой оценкой параметра 1 для нормальной линейной модели регрессии, т. е. необходимо доказать справедливость равенства
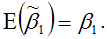
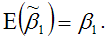
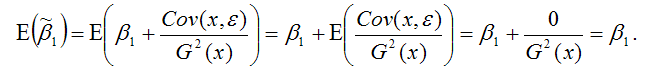
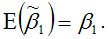
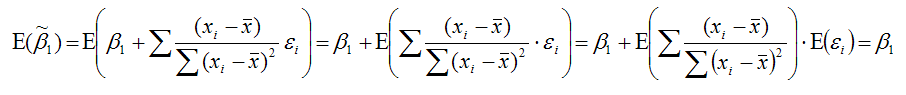
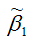 полученная методом наименьших квадратов, является несмещённой оценкой коэффициента 1 нормальной линейной модели парной регрессии.
полученная методом наименьших квадратов, является несмещённой оценкой коэффициента 1 нормальной линейной модели парной регрессии.
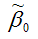 коэффициента 0 нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.
коэффициента 0 нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.
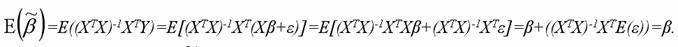
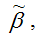 полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов iнормальной линейной модели множественной регрессии.
полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов iнормальной линейной модели множественной регрессии.
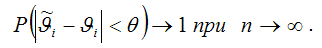
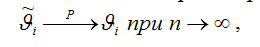
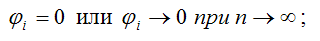
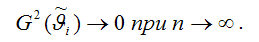
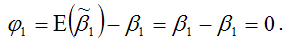
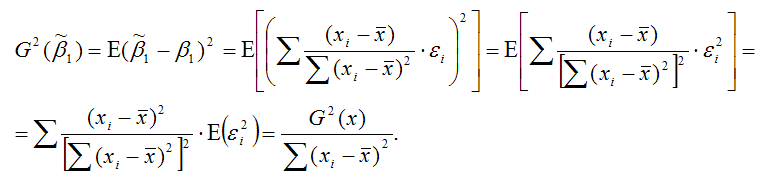
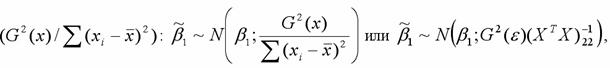
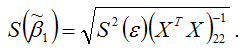
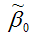 коэффициента 0 нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.
коэффициента 0 нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.
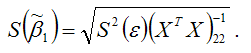
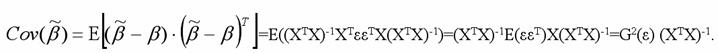
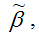 полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов i нормальной линейной модели множественной регрессии.
полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов i нормальной линейной модели множественной регрессии.