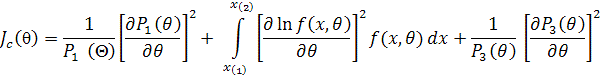Каталог статей

Ширяев А.Ю.

Об оценивании параметров распределений и проверке гипотез по цензурированным выборкам

        Методы оценивания параметров модели, проверка ее адекватности, проверка различных гипотез о параметрах или составляющих модели опираются на имеющуюся априорную информацию, на количество и структуру наблюдений, характеризующих состояние системы. После того, как высказаны предположения о характере вероятностной модели, на основе имеющихся наблюдений обычно решают два вида задач статистического анализа. Во-первых, стараются оценить параметры этой модели таким образом, чтобы она с наибольшей точностью описывала соответствующее явление. Во-вторых, с использованием некоторого критерия проверяют адекватность модели данному явлению. Если модель представляет собой закон распределения, то проверка осуществляется с использованием некоторого критерия согласия. На этапе такой проверки с минимальными вероятностями ошибок гипотеза об адекватности модели должна быть принята, если это действительно так, или отклонена в пользу другой модели, более подходящей. Цель такой проверки – уловить отклонения модели от “истинной”, если они есть, а не постараться их не заметить.

Специфика задач надежности, физическая сущность конкретной предметной области учитываются на этапе выбора вида модели, а методы статистического анализа при этом опираются на вид модели и структуру наблюдаемых данных. В задачах надежности очень часто имеют дело с цензурированными выборками. При этом, вследствие потерь информации из-за цензурирования снижается качество статистических выводов: труднее идентифицировать модель и различать близкие законы распределения, снижается точность оценивания параметров. В то же время при вычислении по цензурированным выборкам оценок максимального правдоподобия (ОМП) сталкиваются со значительной смещён­ностью оценок, при этом величина смещения зависит от степени цензу­рирования и от объёма выборки. При достаточно больших объёмах выборок (возможно применение критериев типа   (Пирсона, Никулина). При простых гипотезах и цензурированных наблюдениях для проверки могут использоваться критерии Реньи, которые в этой ситуации являются “свободными от распределения”. Однако очевидно, что при проверке сложных гипотез они теряют это свойство и, следовательно, необходимы соответствующие исследования распределений их статистик. Отметим кстати, что в этих статистиках вполне обосновано с наибольшим весом берутся наблюдения вблизи точек цензурирования. Применимость критериев согласия типа  типа Колмогорова и типа  Мизеса при цензурированных наблюдениях также требует дополнительных исследований. При этом следует иметь в виду, что проверка сложных гипотез тесно взаимосвязана с проблемой оценивания параметров.

Применение критериев согласия при проверке простых гипотез, по сравнению с проверкой сложных гипотез, снижает мощность этих критериев в два, а то и в два с половиной раза (при одних и тех же близких альтернативах). Причем, при цензурировании способность различения законов в случае простых гипотез ещё снижается. Таким образом, в целях наилучшего различения законов следует осуществлять проверку сложных гипотез, оценивая по выборке параметры закона, соответствующего проверяемой гипотезе. Во-первых, необходимо на основании имеющейся (ограниченной!) информации находить по возмож­ности наиболее точные оценки параметров. Во-вторых, требуется найти распределения статистик критериев согласия, соответ­ствующие данному методу оценивания. Это могут быть как статистики хорошо известных старых, так и вновь предложенных критериев.

При условии, что будет реализован алгоритм эффективного решения первой задачи, решение второй не вызывает в настоящий момент принци­пи­альных трудностей, так как с помощью методов статистического моделиро­вания и с использованием возросших возможностей компьютерной техники с достаточной для практического применения точностью могут быть построены приближенные модели предельных распределений статистик.

То, что касается возможной точности оценивания, то для ОМП ска­лярного параметра она ограничивается снизу асимптотической дисперсией

где n – объем выборки. Информационное количество Фишера по цензуриро­ванной выборке определяется соотношением

где  – вероятность попадания в область цензурирования слева,  - вероятность попадания в область цензурирования справа, а наблюдаемая область лежит в пределах от  до . Если выборка цензурирована только справа, то в выражении исчезает левое слагаемое, только слева - правое слагаемое. Это соотношение позво­ляет судить о потерях информации о параметре рас­пре­деления в зависи­мости от степени цензурирования слева или справа и воз­можной точности оценивания. Чем больше потери информации, тем меньше возможная точность оценивания.

Об эффективности оценивания параметров по цензури­рованной выборке по отношению к оцениванию по полной выборке (без цензурирования) можно судить по величине , где  – количество информации Фишера по полной выборке.