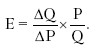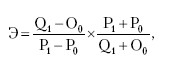Эластичность точечная и дуговая

ТОЧЕЧНАЯ ЭЛАСТИЧНОСТЬ – эластичность, измеренная в одной точке кривой спроса или предложения; является постоянной величиной повсюду, вдоль линии спроса и предложения.

Точечная эластичность представляет собой точный показатель чувствительности спроса или предложения к изменениям цен, доходов и т. д. Точечная эластичность отражает реакцию спроса или предложения на бесконечно незначительное изменение цены, доходов и других факторов. Нередко возникает ситуация, когда необходимо знать эластичность на определенном участке кривой, соответствующем переходу от одного состояния к другому. В данном варианте обычно функция спроса или предложения не задана.

Определение точечной эластичности иллюстрируется на рис. 18.1.

Чтобы определить эластичность при цене Р, следует установить наклон кривой спроса в точке А, т. е. наклон касательной (LL) к кривой спроса в этой точке. Если прирост цены (P) незначителен, прирост объема (Q,), определяемый касательной LL, приближается к действительному. Из этого вытекает, что формула точечной эластичности представляется таким образом:

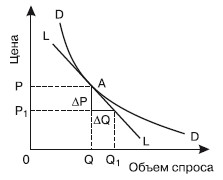
Рис. 18.1. Точечная эластичность

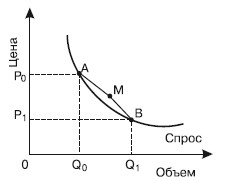
Если абсолютное значение Е больше единицы, спрос будет эластичным. Если абсолютное значение Е меньше единицы, но больше нуля – спрос неэластичен.

ДУГОВАЯ ЭЛАСТИЧНОСТЬ – примерная (ориентировочная) степень реакции спроса или предложения на изменения цены, дохода и других факторов.

Дуговая эластичность определяется как средняя эластичность, или эластичность в середине хорды, соединяющей две точки. В действительности применяются средние для дуги значения цены и объема спроса или предложения.

Эластичность спроса по цене – это отношение относительного изменения спроса (Q) к относительному изменению цены (Р), которое на рис. 18.2 изображено точкой М.

Рис. 18.2. Дуговая эластичность

Дуговая эластичность математически может быть выражена таким образом:

где P₀ – начальная цена;

Q₀ – начальный объем спроса;

P₁ – новая цена;

Q₁ – новый объем спроса.

Дуговая эластичность спроса используется в случаях с относительно большими изменениями цен, доходов и других факторов.

Коэффициент дуговой эластичности, по утверждению Р. Пиндайка и Д. Рубинфельда, всегда лежит где-то (но не всегда посередине) между двумя показателями точечной эластичности для низкой и высокой цен.

Итак, при незначительных изменениях рассматриваемых величин, как правило, используется формула точечной эластичности, а при больших (например, свыше 5 % от начальных величин) используется формула дуговой эластичности.

АЛЛЕИ Рой Джордж Дуглас (р. 1906), английский экономист-математик и статистик. С1944 г. профессор статистики Лондонского университета, читал курс математической экономики в ряде других английских высших учебных заведений. Член советов Экономического и Эконометрического обществ и ряда других научных организаций. Труды Аллена – главным образом учебные пособия по математической экономии, посвященные систематизации и анализу математических методов, используемых при изучении различных экономических проблем. Исходным пунктом экономических исследований он считал не производство, а получение дохода.

Аллен внес существенный вклад в разработку проблемы дуговой эластичности.