| Каталог статей |
|
Гасилов В.В., Карпович М.А., Преображенский М.А. Методы количественного описания негативного воздействия объектов транспортной инфраструктуры на населениеПостановка и решение задачи оптимизации инвестиционных проектов создания и эксплуатации объектов транспортной инфраструктуры требует построения целевой функции (в дальнейшем ЦФ), описывающей их позитивного и негативного влияния на социально-экономические, демографические и экологические процессы. Поскольку параметры ЦФ имеют различную природу, их размерность также неодинакова. Оптимальным по соотношению затраты/отдача методом решения задачи многокритериальной оптимизации является путь введения безразмерных характеристик объектов. В этом подходе стоимостные параметры входят в ЦФ в виде функции от соотношения цена/отдача, а социальные, экологические, демографические факторы и риски – в виде безразмерных множителей и (или) слагаемых.В частности, негативное влияние на население участки автодорог, проходящие через населенные пункты и вблизи их границ, проявляется в шумовом и токсическом загрязнении окружающей среды. При этом значительная доля загрязнений связана с эксплуатацией автомобильного транспорта [1] . Главным образом, это негативное влияние связано с шумовым загрязнением среды и токсическими выбросами в атмосферу. Определение распределения негативных воздействий зависит от топографических, географических и других характеристик среды и представляет собой самостоятельную задачу, решению которой посвящена обширная литература (см. например [2] ). На стадии обоснования инвестиций практически может использоваться только простая модель, описывающая распределение загрязнений в среднем. Наиболее постой является модель линейной зависимости негативного влияния шумового загрязнения от расстояния. При этом в отличие от позитивного воздействия, влияние шумового и токсического загрязнения не имеет стационарной области, а в среднем монотонно убывает с ростом расстояния от источника. Функция негативного шумового влияния (ФНШВ), описывающая сформулированную модель, имеет вид:
где xmax– расстояние от участка автодороги, на котором негативным влиянием можно пренебречь. Как показывают медико-санитарные исследования величину xmax можно значительно уменьшить путем использования зеленых насаждений. Численность населения, испытывающего негативные воздействия (ЧНН), определяется интегрированием произведения ФНШВ и плотности по площади населенного пункта:
Моделируя и в этом случае населенный пункт обобщенным прямоугольником с
линейными размерами Х , У и
минимальным расстояние до автодороги равным Х0 можно легко получить
алгебраические выражения для ЧНН. Во-первых, очевидно, что при условии (населенный пункт
целиком оказывается вне зоны негативного воздействия) значения
Если населенный пункт частично оказывается в зоне негативного воздействия , величина ЧНН определяется значением параметра xmax:
Если дорога проходит непосредственно через населенный пункт, параметр Х0 принимает нулевое значение и формулы (4) и (3) следует применять к каждой из частей, на которые участок автодороги делит поселение, а результаты суммировать. Другой вид загрязнения: токсическое (особенно загрязнение атмосферы) имеет ряд существенных особенностей по сравнению с функций шумового загрязнения [3]. Во-первых, она не имеет области xmax на которой негативным влиянием можно полностью пренебречь. В этом случае функция негативного влияния асимптотически стремится к нулю. Простейший аналитический вид функции, удовлетворяющий этому условию, имеет вид: (5) Во-вторых, число агентов токсического загрязнения весьма велико. Так, например, автомобильные выхлопные газы - смесь примерно 200 веществ и для каждого из них константа с уравнения (5), описывающая скорость уменьшения негативного влияния с расстоянием, сильно зависит от вида токсического загрязнения. В простейшей модели общее действие всех вызывающих загрязнение веществ просто складывается (так называемый принцип суперпозиции) вследствие чего уравнение (5) приобретает вид:
Здесь - относительная степень вредности каждого компонента
смеси. При этом выполняется условие нормировки Как видно из равенства (6), на больших расстояниях от
источника загрязнения (при ) суммарная функция негативного токсического влияния (ФНТВ) определяется только
компонентой смеси с максимальным радиусом действия. В противоположность этому,
на малых расстояниях (при Таким образом, методы, сформулированные в данной работе положения позволяют сформулировать компьютерную модель, как для оптимальных, так и для и наиболее неблагоприятных условий реализации инвестиционного проекта при любых характеристиках задачи. Литература: 1. О.Ф.Балацкий, Л.Г.Мельник, А.Ф.Яковлев “Экономика и качество окружающей природной среды”. Гидрометеоиздат, 2004 г. 2. Сычев А.А., Санников В.М. Комплексный методический подход к оценке генетических последствий загрязнении атмосферного воздуха // Гигиена окружающей среды. – Киев, 1989. – С.149–150. 3. Данилов-Данильян В.И. «Экология, охрана природы и экологическая безопасность» М.: МНЭПУ, 1997 г. 4. Белов С.В. «Безопасность жизнедеятельности» М.: Высшая школа, 1999 г. |
 ,
(1)
,
(1)
 (3)
(3)
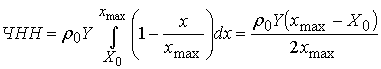 (4)
(4)
 (6)
(6)
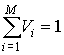 . В литературе описаны кумулятивные
эффекты загрязнения, приводящие к нарушению принципа суперпозиции (6). Однако эти
эффекты проявляются при весьма высоких
степенях загрязнения [4] и редко проявляются в реальных ситуациях.
. В литературе описаны кумулятивные
эффекты загрязнения, приводящие к нарушению принципа суперпозиции (6). Однако эти
эффекты проявляются при весьма высоких
степенях загрязнения [4] и редко проявляются в реальных ситуациях.