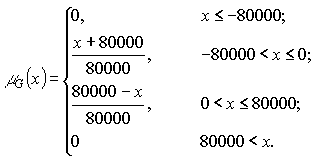С.В. Мордвинов, Э.А. Балдина

Концепции синдиники

Всеобщие закономерности сейчас оформляются и концептуализируются благодаря новой быстрорастущей науке. Это наука об опасности, которая называется синдиника (от греческого слова «kindunos» — «опасность»). Новая область знания имеет дело со всеми аспектами экономической проблемы, поскольку они воздействуют на организации.

Концепции синдиники сейчас применяются к разработке способов предотвращения опасных ситуаций и управлению рисками на уровне малых структурных единиц (предприятий, организаций, фирм).

Принятие финансовых решений в условиях неопределенности и риска - мало изученный вопрос в российской науке и практике.  Для исследования инвестиционных проектов (ИП) недостаточно использовать простейшие модели бухгалтерского учета, поскольку ИП  образуют не только денежные потоки, в нем участвуют лица, управляющие этими потоками. На реализацию ИП оказывает влияние внешняя среда, действия которой, а также ограниченная способность менеджера идентифицировать текущее состояние ИП и прогнозировать будущие денежные потоки, порождают фактор неустранимой неопределенности. Следовательно, применять к анализу финансовых систем классические вероятности и вероятностные случайные процессы не всегда возможно и представляется сомнительным В итоге, исследователь ИП, отказываясь от вероятностного подхода, вынужден использовать в анализе экспертные, минимаксные и другие детерминистские подходы, которые также не  приспособлены для эффективного учета неопределенности поведения финансовых потоков.

Уровень требований финансовых менеджеров, аналитиков и инвесторов к получению и  интерпретации количественных и качественных оценок риска принятия финансовых решений в инвестиционном проектировании постоянно повышается. В с связи с этим встает вопрос о необходимости  качественного совершенствования информативности принятия финансовых решений при инвестиционном проектировании, чем в определенной степени занимается и синдиника.

Среди наиболее популярных методик оценки инвестиционных программ предприятий выделяются вероятностные и интервальные методы оценки, но с ними конкурируют минимаксные подходы к оценке эффективности и рисков инвестирования. Не так давно появилась еще одна разновидность технологий - это методы, основанные на нечетких множествах. Каждые из них имеют свои недостатки и достоинства.

Первой схемой учета неопределенности было изобретение вероятностей. Но начиная с 50-х годов XX века, в академической науке появились работы, ставящие под сомнение сплошную применимость этой теории к учету расплывчатости. Так появились субъективные (аксиологические) возможности.

Однако появление неклассических вероятностей не было единственной реакцией на проблемы применения вероятностей. Необходимо отметить также всплеск интереса к минимаксным подходам, а также зарождение теории нечетких множеств (ТНМ).

Минимаксная схема – это метод оценки проекта, как  последовательность операций, которые дадут наибольший эффект при наименьших рисках. При использовании минимаксного подхода, хотя и не применяющего вероятности отдельных сценариев, большой субъективностью отличается избрание так называемых состояний природы.

Основы ТНМ заложены в фундаментальных работах Лофти Заде. Сам Заде определил нечеткие множества как инструмент построения теории именно возможностей, а не вероятностей. С тех пор научные категории случайности и возможности, вероятности и ожидаемости получают отвлеченное разграничение. С введением нечетких подмножеств оказалось допустимым предсказать будущие значения параметров, которые ожидаемо меняются в определенном расчетном интервале[1].

Прикладные результаты ТНМ не заставили себя ждать. Нечеткая логика, как модель человеческих мыслительных процессов, встроена в системы искусственного интеллекта и в автоматизированные средства поддержки принятия решений.

Многие из изъянов выше приведенных методов исчезают при использовании метода оценки риска инвестиций на основе ТНМ.

Проведенный анализ методов количественной оценки эффективности ИП в обстановке риска и расплывчатости позволяет сделать вывод о том, что существующие методики расчета риска либо элиминируют неопределенность из модели ИП, что незаконно, так как неопределенность является неотъемлемой частью любого прогноза, либо неспособны формально описать и учесть все возможное разнообразие форм неопределенности.

Нечеткие множества - это инструмент расчета возможностей. Во-первых, здесь формируется абсолютный спектр возможных сценариев инвестиционного процесса. Во-вторых, решение принимается не на основе двух оценок эффективности проекта, а по всей базе оценок. В-третьих, ожидаемая эффективность проекта не является точечным показателем, а представляет собой поле интервальных значений со своим распределением ожиданий.

Если соотносить вероятностные, нечетко-множественные и экспертные описания применительно к эффективности решения инвестиционных задач, то можно использовать схему. Видно, что по мере усиления неопределенности классические вероятностные описания уступают место, с одной стороны, субъективным вероятностям, основанным на экспертной оценке, а, с другой стороны, вероятностям, определенным не количественно, а качественно. При этом точечные оценки вероятностных распределений замещаются интервальными и нечеткими.

Значительным преимуществом теории вероятностей является многовековой исторический опыт применения вероятностей и логических схем на их основе. Ухудшение информационной ситуации вызывает к жизни субъективные вероятности, однако тут же возникает проблема достоверности вероятностных оценок.

В случае же применения нечетких чисел к прогнозу параметров не требуется формировать точечные вероятностные оценки, а следует определить расчетный коридор значений прогнозируемых параметров. Здесь возникают инженерные преимущества метода, основанного на нечеткостях, т.к. исследователь оперирует не косвенными оценками, а прямыми проектными данными о разбросе параметров, что есть популярная практика интервального подхода к проектным оценкам[2].

Итак, на стороне вероятностных методов оказывается обычай, а на стороне нечетко-множественных подходов - удобства в инженерном использовании и повышенный уровень обоснованности, поскольку в нечетко-множественный расчет попадают все возможные сценарии развития событий (вообще говоря, образующие непрерывный спектр), чего не скажешь, например, о минимаксном подходе, настроенным на конечное дискретное множество сценариев.

Таким образом, нечеткий метод  является одной из наиболее эффективных математических концепций, направленных на формализацию и обработку неопределенной информации и во многом интегрирующей известные подходы и методы. ТНМ в очередной раз подтверждает популярную истину: применяемый формальный аппарат по своим допустимым возможностям и точности должен быть адекватен семантике, и соответствовать верности используемых исходных данных. Поэтому методы математического анализа эффективно применяются при точных исходных данных.

В итоге можно сказать, что хотя и вероятностные методы оценки рисков ИП изучены в большей мере и более распространены, необходимо отдать должное ТНМ и ее способности оценивать субъективность информации и весь спектр ситуаций инвестирования.

Если поток наблюдаемых данных математической модели наблюдается как статистика, то нет ничего лучше как исследовать эту статистику на основе вероятностных моделей. Но если статистики нет, эксперт встает перед выбором:

- совсем отказываться от применения вероятностей при моделировании Эксперт предполагает, что наблюдаемый параметр может произвольным образом колебаться в пределах некоторого интервала вещественной оси. И все свои последующие выводы эксперт делает на основе этой интервальной оценки;

- вводить в модель субъективные вероятности и вероятностные распределения. Отдельно встает вопрос об обосновании выбора этих оценок, которое производится в рамках  специализированной экспертной модели;

- учитывать неопределенность с применением нечетких.

Проанализируем возможность применения вероятностных, минимаксных моделей и моделей, основанных на ТНМ при оценке риска неэффективности инвестиций. В анализе будем опираться на исследования, касающиеся использования нечетких чисел в анализе риска инвестиций. Выявим наиболее оптимальный вариант метода оценки риска ИП и выскажем предположения о том, является ли нечетко-множественный метод более точным в сравнении с другими известными методами оценки риска неэффективности инвестиций. Для этого воспользуемся не только математическими выводами и моделями, но и конкретными ИП, которые возможны к реализации на исследуемых  предприятиях ЛК г. Лесосибирска.

Перед тем, как назначить задачу оценки риска вложений для самого совокупного эпизода, когда параметры модели плана имеют неотчетливый характер, укажем, что в ряде частных случаев эта проблема уже решена:

- для треугольных чисел общего вида [3], в том числе в аналитической форме;

- когда эффект проекта – произвольно-размытый фактор, а нижнее ограничение на размер эффекта – точечное скалярное число [3].

Теперь мы пришли к необходимости и возможности решить задачу в постановке, когда и эффект, и граничное условие проекта – нечеткие числа произвольного вида. Если неопределенность в части эффекта связана с непредсказуемостью проектных операций, то неясность в части граничного условия порождается отсутствием у владельца проекта четких суждений о нормативах его результативности. При этом возникают частные случаи, когда один или оба числа (эффект и граничное условие) являются:

- интервалами;

- треугольными числами.

В качестве фактора эффективности проекта у нас выступает NPV – чистая текущая стоимость проекта.

Пусть – результативность инвестиций, – граничное условие результативности. Оценим возможность события , что, собственно, и определяет риск того, что проект окажется неэффективным.

- уровень - это степень принадлежности (достоверности). Так как все реализации (NPV, G) при заданном уровне принадлежности  равновозможны, то мы можем определить уровень риска неэффективности проекта как геометрическую вероятность попадания точки (NPV, G) в зону неэффективных инвестиций.

Пусть теперь задан уровень достоверности данных a, и соответствующие интервалы принадлежности, образующие несчетное множество

                            ,                           (1)

                                       .                                  (2)

Степень риска в случае задания определяется для каждого уровня a. Интегральная мера возможности может быть определена через интеграл по мере возможности

                                            ,                                  (3)

где    -  функция принадлежности, в которой       S_a - геометрически площадь зоны неэффективности ИП.

Один из путей повышения экономического и экспортного потенциала лесопромышленных предприятий - максимально возможное вовлечение возобновляемых лесных ресурсов в эксплуатацию на новой технической основе. Решение этих задач требует технического перевооружения, модернизации и реконструкции предприятий.

Рассмотрим три мероприятия, предлагаемые к внедрению на предприятиях ЛК г.Лесосибирска, которые направлены на реконструкцию и повышение экономической эффективности производства:

- переработка горбыля на ОАО «Маклаковский ЛДК»;

- брикетирование отходов на ОАО «Лесосибирский ЛДК№1»;

- внедрение торцовочного станка проходного типа «Vogel-152» на ЗАО «Новоенисейский ЛХК».

Рассмотрим ИП «Приобретение оборудования для лесозавода ЗАО «НЛХК» - внедрение торцовочного станка проходного типа «Vogel-152». Пусть условие эффективности проекта является нечетким числом и имеет вид  , а . Определить степень риска неэффективности инвестиций по ИП.

Функция принадлежности для  NPV имеет вид

Функция принадлежности для G будет выглядеть так

Тогда степень риска для данного проекта составит Risk=0,04+0,0292=0,07≈7%. Рассмотрим ИП «Приобретение линии на ОАО «ЛЛДК№1» - брикетирование отходов». Пусть условие эффективности проекта является нечетким числом и имеет вид  , а  Определить степень риска неэффективности инвестиций по ИП.

. Risk=0,4113≈41,13%.  

Рассмотрим ИП «Приобретение станка на ОАО «МЛДК» - переработка горбыля». Пусть условие эффективности проекта является нечетким числом и имеет вид  , а  Определить степень риска неэффективности инвестиций по ИП. Risk=0,17-0,0049=0,1728≈17,28%.

Таким образом, попытаемся свести результаты вычислений согласно разным моделям оценки в сводную таблицу для оптимизации уровня риска и охарактеризуем решение, которое возможно к принятию ЛПР (табл. 1).

Согласно таблицы 1, наиболее оптимальным методом оценки риска ИП предприятий ЛК г. Лесосибирска является метод, основанный на ТНМ, так как он дает наиболее точную оценку состояния неопределенности и реализации ИП.

Таблица 1 - Выбор и оптимизация уровня риска инвестиционных проектов предприятий лесного комплекса г. Лесосибирска 

ИП предприятия	Варианты методов оценки риска инвестиционных проектов предприятий, %			Оптимальный уровень риска, %	Решение, принимаемое ЛПР
	Нечетко-множественные модели	Минимаксные модели	Вероятностные (имитационные) модели
Переработка горбыля на ОАО «МЛДК»	17,28 - пограничный уровень риска	NPV=5571 руб. (NPV>0)  - ИП можно принять к рассмотрению	23,32 - неприемлемый уровень риска	17,28	ЛПР следует отказаться от реализации ИП или принять в зависимости от предполагаемого будущего состояния организации.
Брикетирование отходов на ОАО «ЛЛДК№1»	41,13 - неприемлемый уровень риска	NPV=-416941 руб. (NPV<0)  - ИП не рекомендуется	42,2 - неприемлемый уровень риска	-	Отказ от реализации ИП
Внедрение торцовочного станка проходного типа «Vogel-152» на ЗАО «НЛХК»	6,9 - приемлемый уровень риска	NPV=74515 руб. (NPV>0)  - ИП можно принять к рассмотрению	14,01 - приемлемо-средний уровень риска	6,9	Принять ИП к реализации

Согласно расчетам ИП предлагаемый к реализации на ОАО «ЛЛДК№1» является неэффективным, таким образом, в дальнейшем мы не будем рассматривать экономический эффект. Рассмотрим и рассчитаем экономические эффекты для двух ИП (таблица 2).

Таблица 2 - Оценка экономического эффекта от использования нечетко-множественного метода

Показатель	ОАО «МЛДК»	ЗАО «НЛХК»
Номер периода	1	1
Рентабельность капитала, %	47,17	13,07
Стоимость ИП, руб.	241000	338070
Уровень риска по вероятностной модели, %	23,32	14,01
Уровень риска по нечетко-множественной модели, %	17,28	6,90
Резервный капитал, создаваемый в случае использования вероятностного метода оценки риска (рассчитываемый произведением уровня риска на стоимость ИП), руб.	56201,2	47363,6
Резервный капитал, создаваемый в случае использования нечетко-множественного метода оценки риска (рассчитываемый произведением уровня риска на стоимость ИП), руб.	41644,8	23326,8
Экономия резервных средств, руб.	14556,4	24036,8
Экономический эффект от учета риска, руб.	21422,6	27178,5

Таким образом, применение ТНМ в оценке эффективности и риска ИП дает экономический эффект за счет снижения резервного фонда путем более точной оценки риска в условиях неопределенности. Высвобожденные таким образом  денежные средства позволят задействовать новые финансовые ресурсы в хозяйственной и иной деятельности предприятия для повышения уровня благосостояния его собственников в будущем.

Библиографический список:

1. Алтунин, А.Е., Семухин, М.А. Модели и алгоритмы принятия решений в нечетких условиях[Текст]/ А.Е. Алтунин, М.А. Семухин. - Тюмень: изд-во ТГУ, 2003. - 352с.

2. Бочарников, В.П. Fuzzy-технологии: математические основы моделирования в экономике[Текст]/ В.П. Бочарников. - СПб: Наука РАН, 2001. -386с.

3. Деревянко, П.М. Модели и методы принятия решений по распределению реальных инвестиций с применением теории нечетких множеств[Текст]/П.М. Деревянко. - С.-Пб: ДисЭконом, 2006. - 224с.