|
Зинченко А.Б.
Крайние точки многогранников игр большого босса
Игры большого босса (big boss games) [1] являются подклассом
сбалансированных кооперативных игр 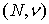 , где - множество
игроков, , где - множество
игроков, 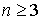 , - характеристическая
функция. Босс (главный игрок) имеет большие возможности, чем остальные (слабые)
игроки. Два основных свойства характеризуют такие игры: босс должен иметь право
вето, а продуктивность слабых игроков – возрастать при их объединении. Введено
несколько типов игр большого босса (не монотонные, монотонные, тотальные, обобщенные,
сильного босса), каждый из которых имеет многочисленные приложения и образует
конус в пространстве , - характеристическая
функция. Босс (главный игрок) имеет большие возможности, чем остальные (слабые)
игроки. Два основных свойства характеризуют такие игры: босс должен иметь право
вето, а продуктивность слабых игроков – возрастать при их объединении. Введено
несколько типов игр большого босса (не монотонные, монотонные, тотальные, обобщенные,
сильного босса), каждый из которых имеет многочисленные приложения и образует
конус в пространстве 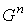 . Представляет интерес, например, использование кооперативной
игры с боссом для анализа распределения ²рыночной силы² в цепи поставщиков российского газа [2]. . Представляет интерес, например, использование кооперативной
игры с боссом для анализа распределения ²рыночной силы² в цепи поставщиков российского газа [2].
Для исследования поведения решений на
подмножествах важно иметь явное описание
их экстремальных элементов. Направляющими векторами конуса 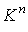 не монотонных игр
большого босса являются простые игры, принадлежащие [3]. Для монотонных
игр это уже не верно. Используя (0-1)-нормализацию, конус можно трансформировать
в многогранник, крайние точки которого взаимно однозначно соответствуют
направляющим векторам конуса. Это преобразование не меняет структуры игры и
свойств многих ее решений, поэтому, для простоты изложения, будем рассматривать
многогранник не монотонных игр
большого босса являются простые игры, принадлежащие [3]. Для монотонных
игр это уже не верно. Используя (0-1)-нормализацию, конус можно трансформировать
в многогранник, крайние точки которого взаимно однозначно соответствуют
направляющим векторам конуса. Это преобразование не меняет структуры игры и
свойств многих ее решений, поэтому, для простоты изложения, будем рассматривать
многогранник 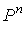 нормализованных
монотонных игр большого босса, предполагая, что боссом является первый игрок. Насколько
известно автору, проблема характеризации нецелочисленных крайних точек
многогранника пока не решена. нормализованных
монотонных игр большого босса, предполагая, что боссом является первый игрок. Насколько
известно автору, проблема характеризации нецелочисленных крайних точек
многогранника пока не решена.
В данном докладе дается описание всех крайних
точек многогранника 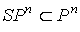 игр, симметричных
относительно коалиции слабых игроков , и крайних точек многогранника игр, симметричных
относительно коалиции слабых игроков , и крайних точек многогранника 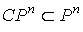 выпуклых игр большого
босса. Для некоторых подмножеств множества получено явное представление
соответствующих значений Шепли выпуклых игр большого
босса. Для некоторых подмножеств множества получено явное представление
соответствующих значений Шепли 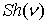 и консенсус-значений [4]. Многогранник и консенсус-значений [4]. Многогранник 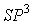 игр с боссом и двумя
симметричными слабыми игроками имеет только две крайние точки и игр с боссом и двумя
симметричными слабыми игроками имеет только две крайние точки и 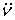 , где , , где , 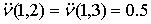 , а остальные значения , , а остальные значения , 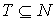 , определены условиями , определены условиями
, 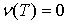 , или , или 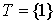 . (1) . (1)
Пусть , 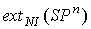 - множества
целочисленных и нецелочисленных крайних точек многогранника , а - множества
целочисленных и нецелочисленных крайних точек многогранника , а 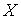 - множество 0-1 векторов . Следующая теорема показывает, что все нецелочисленные
крайние точки - множество 0-1 векторов . Следующая теорема показывает, что все нецелочисленные
крайние точки 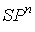 принадлежат его -мерной грани и находятся во взаимно однозначном соответствии
с элементами множества принадлежат его -мерной грани и находятся во взаимно однозначном соответствии
с элементами множества 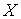 . .
Теорема
1. Пусть и 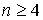 , тогда: , тогда:
(a) ;
(b)  тогда и только тогда,
когда существует такой вектор , что тогда и только тогда,
когда существует такой вектор , что 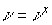 , где , , где , 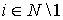 , , если , , если 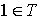 и , и ,
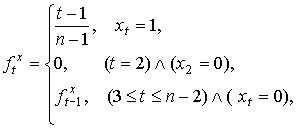
а остальные значения определены (1);
(c) 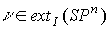 тогда и только тогда,
когда существует такое , что тогда и только тогда,
когда существует такое , что 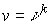 , где , где
(2)
Следствие
1. 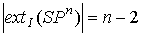 , . , .
Следствие
2. Игры 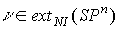 имеют одинаковые -ядра имеют одинаковые -ядра 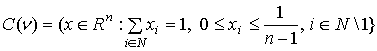 . Все игры имеют одноэлементное . Все игры имеют одноэлементное 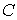 -ядро , где -ядро , где 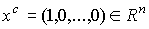 . .
Содержательная
интерпретация игр приведена в [5].  -ядро является основной концепцией решения кооперативной игры
. Принадлежность -ядро является основной концепцией решения кооперативной игры
. Принадлежность 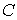 -ядру считается
положительным свойством других решений, а
идеальным - случай, когда -ядро состоит
из единственного дележа. Но, как показывает следствие 2, единственный элемент -ядру считается
положительным свойством других решений, а
идеальным - случай, когда -ядро состоит
из единственного дележа. Но, как показывает следствие 2, единственный элемент 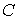 -ядра игр дискриминирует экономических
агентов -ядра игр дискриминирует экономических
агентов 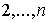 , т.к. вся прибыль от кооперации достается боссу,
несмотря на его нулевые собственные возможности , т.к. вся прибыль от кооперации достается боссу,
несмотря на его нулевые собственные возможности 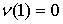 . Переговорное множество, -ядро, лексикографическое ядро, . Переговорное множество, -ядро, лексикографическое ядро, 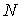 -ядро, -значение, -ядро, -значение, 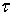 -значение всех игр совпадают с -значение всех игр совпадают с 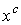 , поэтому представляет интерес поведение на решений, не являющихся
селекторами , поэтому представляет интерес поведение на решений, не являющихся
селекторами  -ядра. -ядра.
Теорема 2. Значение
Шепли и консенсус-значение игры , соответствующей 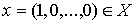 , и игры , определенной (2), имеют вид: , и игры , определенной (2), имеют вид:
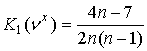 , ;. , ;. 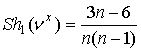 , ; , ; 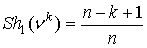 , ; , ; 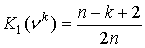 , , , , 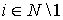 . .
Из теоремы 2 следует, что
значение Шепли (при бездотационном принципе распределения благ) и консенсус-значение
(при компенсационном принципе) более согласованы с экономическими ситуациями,
порождающими игры , чем единственный дележ 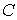 -ядра. Например, для игр с шестью участниками получаем
следующие диапазоны изменения выигрышей [6]: -ядра. Например, для игр с шестью участниками получаем
следующие диапазоны изменения выигрышей [6]:
, 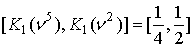 , ,
, 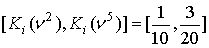 , . , .
Численный эксперимент показал, что консенсус-значение игры
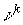 , , часто совпадает с его коалиционным аналогом [5] для
структуры , , часто совпадает с его коалиционным аналогом [5] для
структуры 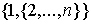 , соответствующей ситуации, когда все слабые агенты
объединяются и (внутри максимальной коалиции ) противостоят боссу как единый игрок. , соответствующей ситуации, когда все слабые агенты
объединяются и (внутри максимальной коалиции ) противостоят боссу как единый игрок.
Последняя теорема доклада
показывает, что многогранник выпуклых игр большого босса - полностью
целочисленный, а множество его крайних точек является подмножеством игр единогласия
(unanimity games) 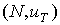 , где , если , где , если 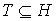 , и в остальных случаях. , и в остальных случаях.
Теорема 3. 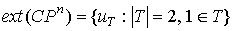 . .
Заметим, что , т.е. 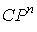 является выпуклой
оболочкой подмножества крайних точек общего многогранника . является выпуклой
оболочкой подмножества крайних точек общего многогранника .
Литература:
1.
Muto S., Nakayama M., Potters J.,
Tijs S. On big boss games // The Economic Studies Quarterly. 1988. № 39. P.
303-321.
2. Hubert F., Ikonnikova S. Investment Options and
Bargaining Power the Eurasian Supply Chain for Natural Gas // The Journal of
Industrial Economics. 2011. Vol. 59. № 1. P. 275-293.
3. Potters J., Poos R., Tijs S., Muto S. Clan games // Games and
Economic Behavior. 1989. № 1. P. 275-293.
4. Ju Y., Born P., Rays P. The consensus value: a new solution
concept for cooperative games // Social Choice and Welfare. 2006. Vol. 28. № 4. P. 85-703.
5. Зинченко А.Б.,
Мироненко
Г.В., Провоторова
П.А. Консенсус-значение
для игр с коалиционной структурой // Математическая теория игр и ее приложения.
2010. Том 2. Выпуск 1. С. 93-106.
6. Provotorova P.A., Zinchenko A.B. On the extreme
points of polytopes of some subclasses of big boss games // Abstracts of the
Fifth International Conference «Game Theory and Management». St. Petersburg. 2011. P. 188-191.
|
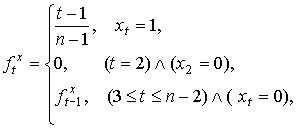
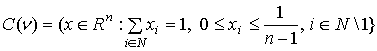 . Все игры имеют одноэлементное
. Все игры имеют одноэлементное 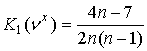 , ;.
, ;. 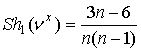 , ;
, ;