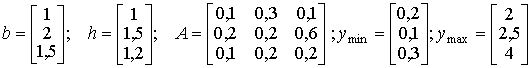| Каталог статей | ||||||
|
Квасова Н.В., Васильев Е.М. Исследование динамических процессов в региональной экономикеЗадача моделирования и анализа динамических процессов региональной экономики вытекает из необходимости государственного управления этими процессами и оценки ожидаемой реакции отраслей региона на то или иное управляющее воздействие. В качестве таких воздействий будем рассматривать: u(t) – общий объём инвестиций в регион; uд,i(t) – директивный объём инвестиций в отрасль i; ymax,i(t) – текущий предельный уровень конечного потребления продукции отрасли i, включающий государственные закупки; aji(t) – коэффициенты прямых материальных затрат,
где bi
– коэффициент прироста валового выпуска xi ; hi
– коэффициент приростной капитализации от внешних инвестиций ui(t); di(t) –
инновационный мультипликатор: , si(t)—затраты отраслью i промежуточной
продукции: Примем n=3 и зададимся условными параметрами системы:
Рассмотрим влияние инвестиций. Инвестиции региона (u(t³2)=10, uд,i=0) распределяются пропорционально мультипликатору di(t): d1=0,6; d2=0,3; d3=0,1.
Рис. 1 подтверждает распределённое влияние инвестиций на все отрасли. Наиболее интенсивное изменение y(t) наблюдается в отрасли 1. Введение директивных инвестиций uд,1(t³2)=0; uд,2(t³2)=2; uд,3(t³2)=6 представлено на рис. 2 и свидетельствует об их дифференцированном влиянии: состояние региона без инвестиций характеризовалось преобладающим развитием отраслей 1 и 2, не сбалансированным с темпами роста производства отрасли 3, и введение директивных инвестиций преимущественно в отрасль 3 позволило восстановить сбалансированный рост конечного потребления всех отраслей.
Инновационную деятельность отраслей покажем на примере уменьшения коэффициента прямых материальных затрат a23=0,6 до значения a23=0,4, рис. 4.
Как и следовало ожидать, указанное изменение положительно сказалось на конечном потреблении всех отраслей и не только увеличило y2(t), но и дало возможность устранить спад y3(t) в результате роста условно чистого дохода в отрасли 3 и направления части этого дохода на капитальные вложения.
Литература: 1. Альсевич В.В. Введение в математическую экономику. Конструктивная теория / В.В. Альсевич. – М.: Едиториал УРСС, 2005. – 256 с. 2. Тарасевич Л.С. Макроэкономика /Л.С. Тарасевич, П.И. Гребенников, А.И. Леусский. – М.: Высшее образование, 2006. – 654 с. | ||||||
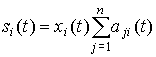 , , mc,i(t) – мультипликатор
неудовлетворённого спроса на производственное и конечное потребление:
, , mc,i(t) – мультипликатор
неудовлетворённого спроса на производственное и конечное потребление: 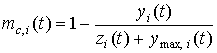 , zi(t)—производственное потребление: , yi(t)=xi(t)-zi(t); ymax,i(t) – текущий предельный
уровень конечного потребления продукции; gc,i(t) –
ограничитель спроса на конечное потребление продукции отрасли i:
, zi(t)—производственное потребление: , yi(t)=xi(t)-zi(t); ymax,i(t) – текущий предельный
уровень конечного потребления продукции; gc,i(t) –
ограничитель спроса на конечное потребление продукции отрасли i: 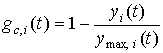 , gп,i(t) –
ограничитель производственного потребления: , ymin,j(t) –
минимальный уровень конечного потребления продукции отрасли j, например, обязательные государственные поставки; b – степень влияния gп(t).
, gп,i(t) –
ограничитель производственного потребления: , ymin,j(t) –
минимальный уровень конечного потребления продукции отрасли j, например, обязательные государственные поставки; b – степень влияния gп(t).