| главная :: экономика :: право :: сертификация :: учебники :: поиск | ||||||||||||||||||||||||||||
| Каталог статей | ||||||||||||||||||||||||||||
|
к.т.н. Ахметов Кулмагамбет Ахметович, докторант Ph.D, Балапанова Эльмира Салимовна Казахский Национальный Аграрный Университет Применение экономико-математических методов и информационных технологий для эффективного развития аграрного бизнесаВ современных условиях обеспечение эффективной деятельности всех секторов экономики невозможно без использования математических методов, моделей и информационных технологий. Современное сельское хозяйство, как одна из важнейших отраслей народного хозяйства, имеет ряд специфических особенностей, которые способствуют успешному применению экономико-математических методов и информационных технологий для эффективного развития агроформирований и аграрного бизнеса в целом. В настоящее время неизмеримо возрастает роль методов оптимизации в принятий управленческих решений на уровне сельскохозяйственных пред-приятий, так как значительно усложнились задачи эффективной организации производства и хозяйствования. Появляется масса проблем эффективного хозяйствования на уровне агроформирований, а также возникают новые, связанные с оптимизацией рынка сельскохозяйственных продуктов. Сегодня применение математических методов в среде информационных технологий для решения таких оптимизационных задач имеет важное значение. И их можно отнести к числу инновационных способов решения таких проблем в аграрной науке. Важный класс прикладных оптимизационных задач образуют задачи о смесях. Такие задачи возникают при выборе наилучшего способа смеше-ния исходных ингредиентов для получения смеси с заданными свойствами. Смесь должна иметь требуемые свойства, которые определяются количес-твом компонентов, входящих в состав исходных ингредиентов. Как правило, известны стоимостные характеристики ингредиентов и искомую смесь требуется получить с наименьшими затратами. Для многопродуктовых задач, в которых требуется получить несколько смесей, характерным является критерий максимизации прибыли. Важный класс прикладных оптимизационных задач образуют задачи о смесях. Такие задачи возникают при выборе наилучшего способа смешения исходных ингредиентов для получения смеси с заданными свойствами. Смесь должна иметь требуемые свойства, которые определяются количес-твом компонентов, входящих в состав исходных ингредиентов. Как правило, известны стоимостные характеристики ингредиентов и искомую смесь требуется получить с наименьшими затратами. Для многопродуктовых задач, в которых требуется получить несколько смесей, характерным является критерий максимизации прибыли. Задача оптимального смешения встречаются во многих отралях народного хозяйства: · металлургия · парфюмерия · пищевая промышленность · фармакология · селькое хозяйство Примерами задач о смесях в сельском хозяйстве могут служить определение кормового рациона скота на животноводческих фермах, оптимального соотношения минеральных удобрений, для определения минимальной стоимости кормовых рационов при заданном количестве кормов (по видам и содержащимся в них питательным веществам), составление рецептуры лекарственных средств для животных, и т.п. Рассмотрим содержание математической модели задачи составления смеси. Обозначем через аij удельное содержание вещества Bj в сырье типа Si и его содержание хі (процент или доля или в других единицах измерения) в одной единице смеси. Пусть смесь создается с n типов сырья (количество исходных ингредиентов) и сбалансируется с m веществами (количество компонентов в смеси). По условиям создания смеси вещества Bj в ней должна быть от bimin до bjmax процентов Отсюда получаем m ограничений
К этим ограничениям необходимо добавить еще одно ограничение, которое, собственно, и отличает модели составления смесей от других производственных моделей. ♦ Это ограничение называется условием материального баланса и записывается в виде следующего равенства: x1 +x2 +... + xn= 100, если xi обозначает процентное содержание в смеси сырья Si;, или x1 +x2 +... + xn= 1, если xi обозначает долевое содержание в смеси сырья Si. Здесь мы впервые встретились с ограничением в виде равенства. Обычно в моделях оптимизации избегают применять ограничения в виде равенств, поскольку они могут вызвать некоторые затруднения при поиске оптимального решения. Однако в моделях некоторых типов, подобных рассматриваемой модели, такие ограничения неизбежны, и их не следует бояться, хотя и следует по возможности заменять неравенствами. Для полноценной модели оптимизации не хватает самого главного— целевой функции, т.е. критерия, в соответствии с которым будут отбираться возможные варианты смеси. Допустим, таким критерием будет минимум стоимости смеси. Обозначим через с1, с2, ...,сп удельные стоимости сырья S1, S2,.... Sn сответственно. Тогда удельную стоимость смеси можно подсчитать по формуле:
если переменные x1, x2, ... xn представляют Долевое содержание в смеси соответствующего сырья. Если переменные решения обозначают процентное содержание сырья, то значение, вычисленное по этой формуле, пропорционально (в 100 раз больше) удельной стоимости смеси. ♦ В любом случае функцию:
можно взять в качестве целевой функции, которую следует минимизировать. Как правило, модели составления смесей будут линейными моделями оптимизации. Однако рассмотренный далее пример модели составления смеси показывает, что такие модели могут быть и нелинейными. Агрофирме «Береке» необходимо внести минеральные удобрения под новую для него сельхозкультуру. По новым инновационным рекомендациям под эту культуру в расчете на один гектар надо вносить 10 кг азота, 8 кг фосфора и 5 кг калия. На рынке имеется четыре вида подходящих удобрений разных производителей. Содержание необходимых элементов в килограммах и цена в расчете на 1 тонну для этих видов удобрений показаны в табл. 1, которые определены агрофирмой в районном отделении «Маркетинговые исследования». Таблица 1. Содержание необходимых элементов (в кг) в 1 тонне удобрений на рынке производства и их цена в расчете на 1 тонну, тенге
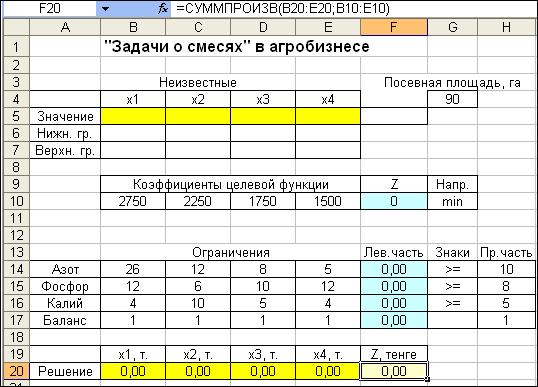
Агрофмирме необходимо подсчитать, сколько ему нужно купить удобрения каждого типа и в каких пропорциях их смешивать, чтобы было и подешевле и чтобы содержание необходимых элементов в смеси было не меньше, чем советуют ученые. Всего агрофирма планирует внести эти удобрения на площади 90 гектаров. Модель смеси для агрофирмы «Береке». Сначала составляем математическую модель. В качестве переменных решения возьмем доли x1, x2, x3, x4 удобрений вида №1, №2, №3 и №4 соответственно в тонне смеси, вносимой на один гектар. Целевая функция составляется следующим образом: Z=2750 x1 + 2250 x2 + 1750x3 + 1500x4 → min Ограничения: 26 x1 + 12 x2 + 8 x3 + 5 x4 ≥ 10 (ограничение по азоту), 12 x1 + 6 x2 + 10 x3 + 12 x4 ≥ 8 (ограничение по фосфору), 4 x1 + 10 x2 + 5 x3 + 4 x4 ≥ 5 (ограничение по калию), x1 + x2 + x3 + x4 =1 (условие баланса ), x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0 (условия неотрицательности). Табличная модель, построенная по этой математической модели, приведена на рис. 1.1 В ячейке F10 вычислена стоимость 1 т новой смеси по формуле: =СУММПРОИЗВ(B10:E10; $В$5:$Е$5).
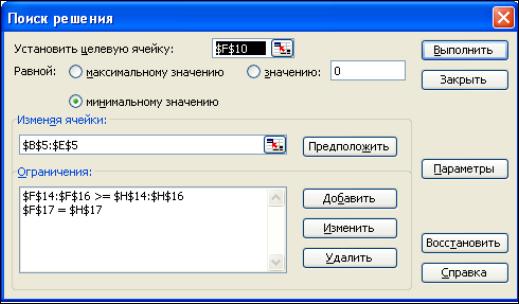
Рис. 1.1. Табличная модель для решения задачи Обращаем внимание на строку Решение табличной модели, где переменные решения сразу пересчитываются в тонны удобрений, которые необходимо закупить для внесения на все 90 гектаров, причем количество гектаров введено в отдельную ячейку G4, и это количество можно легко варьировать. Формула пересчета показана на рис. 1.1 в строке формул. На все 90 га вычисляется необходимое количество удобрение №1 по простой формуле в ячейке B20 (=B5*$G$4) и эта же формула, путем использования алгоритма копирования автоматической настройкой на новый адрес протаскивается до ячейки E20. В результате в диапозоне ячеек B20:E20 определяется необходимое количество всех видов удобрений на все 90 га. После этого, используя коэффициенты целевой функции, установленые в диапозоне ячеек B10:E10, можно вычислить общую стоимость удобрений в ячейке F20 по формуле, которая показана на строке fx - мастер функции: =CУММПРОИЗВ(B10:E10;B20:E20) или же по простой формуле: =G4*F10. Диалоговое окно Поиск решения, при котором найдено решение, показано па рис. 1.2. В диалоговом окне Параметры поиска решения должны быть установлены флажки Линейная модель, Неотрицательные значения и Автоматическое масштабирование.
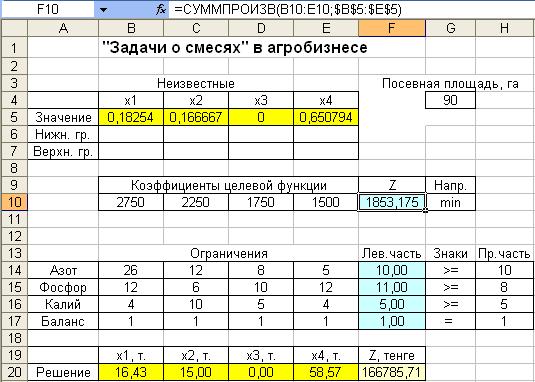
Рис. 1.2. диалоговое окно Поиск решения для решения задачи Результаты решения задачи агрофирмы показаны в рис. 1.3. Анализ полученного решения проводить не будем, так как на 1 га нужно вносить ровно одну тонну смеси удобрений, выгодно ли вести изменение в модели задачи? Безусловно, поэтому необходимо ввести в модель еще одну переменную, которая обозначается y и которая будет означать количество смеси удобрений, вносимой на один гектар. Во-первых, посмотрим на целевую функцию. Сейчас она подсчитывает стоимость тонны смеси, вносимой на один гектар.
Рис. 1.3. Результаты решения задачи Если на гектар вносится у тонн смеси, то теперь целевая функция подсчитывает стоимость у тонн смеси, вносимой на один гектар. Для этого целевая функция должна иметь вид Z= у∙(2750 x1 + 2250 x2 + 1750x3 + 1500x4) → min. Во-вторых, посмотрим на ограничения, например, на ограничение по азоту. Сейчас формула 26x1 + 12x2 + 8x3 + 5x4 подсчитывает количество азота в одной тонне смеси. Если имеем у тонн смеси, то в этих у тоннах содержится у∙(26 x1 + 12 x2 + 8 x3 + 5 x4) килограммов азота. Таким образом, теперь ограничения будут иметь следующий вид: у (26 x1 + 12 x2 + 8 x3 + 5 x4) ≥ 10 (ограничение по азоту); у (12 x1 + 6 x2 + 10 x3 + 12 x4) ≥ 8 (ограничение по фосфору); у (4 x1 + 10 x2 + 5 x3 + 4 x4) ≥ 5 (ограничение по калию); x1 + x2 + x3 + x4 =1 (условие баланса), x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0 (условия неотрицательности). Как видно, в модель необходимо внести самые минимальные измене-ния, которые показаны на рис. 4.4. Пусть значение новой переменной у содержится в ячейке F5. Формулы в ячейках F10 и F14:F16 надо переделать таким образом, чтобы те значения, которые вычислялись = СУММПРОИЗВ(B10:E10;$B$5:$E$5)*$F$5 и в ячейке F14 будет формула: = СУММПРОИЗВ(B14:E14;$B$5:$E$5)*$F$5. Далее эту формулу можно скопировать в диапазон F14:F16. В строке Решение также сделаны небольшие изменения так, чтобы подсчитать количество удобрений каждого вида, используемого на все 90 гектаров. Соответствующая формула для удобрения 1 показана на рис. 1.4 в строке формул. В ячейке B20 формула записывается в следующем виде: = B5*$F$5*$G$4. Аналогичные формулы используются в ячейках С20:Е20. Формула в ячейке F20 осталась без изменений.
Рис. 1.4. Новая модель и новое решение После внесенных изменений модель стала нелинейной, поскольку в формулах целевой функции и функций ограничений появились произведения переменных уx1, уx2 , уx3 и уx4. Это говорит о том что, данная модель теперь может не иметь решения или иметь их несколько. Запустим средство Поиск решения, чтобы прояснить ситуацию. В диалоговом окне Поиск решения, которое показано на рис. 1.5, изменения небольшие - надо только добавить в поле Изменяя ячейки новую изменяемую ячейку F5. В диалоговом окне Параметры поиска решения следует обязательно снять флажок Линейная модель, оставив флажки Неотрицательные значения и Автоматическое масштабирование. Щелкаем в окне Поиск решения на кнопке Выполнить и получаем решение, показанное на рис. 1.4.
Рис. 1.5. диалоговое окно Поиск решения для нового решения задачи Новое решение показывает, что можно вносить (1 – 0,8125 = 0,1875 тонн) меньше удобрений, при этом еще получается экономия средств в (166785,71 – 150245,54 = 16540,17 тенге). Таким образом, В современных условиях инновационные методы экономико-математического моделирования является самым мощным инструментом, применяемым в сфере управления бизнесом, в том числе агробизнесом. В данной статье рассматриваются оптимизационные модели для определения рациональной структуры минеральных удобрений. | ||||||||||||||||||||||||||||
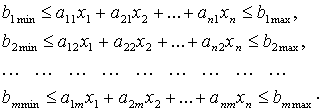
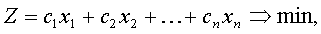
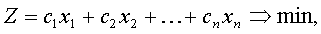

 ранее, теперь еще умножались на значение у, т.е. умножались на содержимое ячейки F5. Например, в ячейке F10 теперь будет формула:
ранее, теперь еще умножались на значение у, т.е. умножались на содержимое ячейки F5. Например, в ячейке F10 теперь будет формула: