Андриенко В.М., Богданова В.А.

Одесский национальный политехнический университет

Стохастический тренд индекса ПФТС

Состояние фондового рынка играет важную роль для стабильного развития экономики. Крах фондового рынка, то есть сильное падение (шок) курсовой стоимости ценных бумаг за короткий промежуток времени, может вызвать спад и депрессию в экономике. Разразившийся мировой финансовый кризис осени 2008 г. не только остановил поступательное развитие украинского фондового рынка, но и отбросил его назад. Следует ожидать, что его негативные последствия достаточно долго будут сказываться на состоянии экономики Украины. Поэтому на первый план выдвигается задача оценки состояния и тенденции развития ситуаций на фондовом рынке. Проблема анализа и прогнозирования фондовых рынков, насчитывающая не одно столетие, сохраняет свою остроту и до настоящего времени и делает работу финансовых аналитиков всегда востребованной и актуальной. Это обусловлено сложностью фондового рынка, наличием нелинейных и динамических связей между основными его параметрами, вероятностным характером протекающих на нем процессов. В связи с этим имеются повышенные требования к качеству экономико-математического инструментария, применяемого для решения этой проблемы. В настоящее время разработаны соответствующие модели и методы анализа и прогнозирования фондовых рынков в рамках таких направлений, как технический и фундаментальный анализ, теория оптимизации инвестиционного портфеля, нелинейной динамики (хаоса) и фрактального рынка. Однако, задача построения адекватного инструментария далека от своего завершения, о чем свидетельствуют многочисленные факты неудовлетворительных прогнозов их динамики. Этим обуславливается необходимость разработки новых и более совершенных методов анализа и прогнозирования. Острота и научная значимость решения данной проблемы в наибольшей степени очевидна применительно к молодым развивающимся фондовым рынкам (в частности, для украинского рынка), специфика которых не всегда в полной мере учитывается имеющимся инструментарием. Построение математических моделей, позволяющих лучше понять структуру и поведение рынка, как единого целого, так и его составляющих, долгое время привлекали и продолжают привлекать внимание исследователей и практиков.

Основными индикаторами фондового рынка являются индексы, рассчитываемые на основании котировок определенной группы ценных бумаг. В зависимости от того, какие компоненты содержит индекс, он может отражать поведение определенной группы акций или всего фондового рынка. Индекс Украинского фондового рынка ПФТС (первая фондовая торговая система) признан международной финансовой корпорацией (МФК) как единственный индекс, используемый этой организацией при мониторинге внутреннего состояния украинского фондового рынка. Индекс определяет средний уровень наиболее ликвидных украинских акций, которые имеют наибольшую рыночную капитализацию. Информацию о состоянии индекса ПФТС публикует на своем сайте «Первая фондовая торговая система», которая представляет собой электронную биржу ценных бумаг Украины и поддерживает работу национальной электронной системы торговли ценными бумагами в режиме «online».

Большинство математико-статистических методов имеет дело с моделями, в которых наблюдения предполагаются независимыми и одинаково распределенными. При этом основное внимание уделяется проблемам идентификации моделей, отбору эндогенных и экзогенных показателей, но почти не обращается внимания на формальный анализ структуры исходных статистических рядов. Зависимость между наблюдениями чаще всего рассматривается как помеха в эффективном применении этих методов. Однако разнообразные данные в экономике, социологии, финансах, коммерции и других сферах человеческой деятельности поступают в форме временных рядов, в которых наблюдения взаимно зависимы, и характер этой зависимости как раз и представляет главный интерес для исследователя. Принципиальные отличия временного ряда от последовательности наблюдений, образующих случайную выборку, заключаются в следующем:

- в отличие от элементов случайной выборки члены временного ряда не являются независимыми;

- члены временного ряда не обязательно являются одинаково распределенными.

Аналитически временной ряд можно выразить уравнением вида:

,

Где 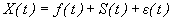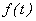- тренд ( долговременная тенденция ) развития;

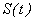- сезонная ( периодическая) компонента;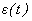

- случайная величина ( случайный компонент ).

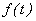Функция определяет общую тенденцию развития изучаемого явления. Тренд может быть выражен как детерминированной, так и случайной функциями, либо их комбинацией. Компоненты временного ряда 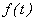, 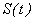и 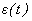не наблюдаемы, они являются теоретическими величинами. Выявление этих компонент и является задачей анализа. В рядах с детерминированным трендом влияние предыдущих шоковых воздействий (резких изменений) затухает с течением времени, а в рядах со стохастическим трендом такое затухание отсутствует, и каждый отдельный шок влияет с одинаковой силой на последующие значения ряда. Такие ряды называют «временные ряды с долговременной корреляционной зависимостью» (time series with long memory) или «ряды с долговременной памятью». Каждое наблюдение таких рядов коррелирует до некоторой степени с последующими наблюдениями, а для корреляционной функции характерно медленное убывание. Детерминированные компоненты 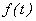и 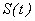обнаруживается с помощью спектральнго анализа [1]. Детерминированная составляющая имеет неограниченную спектральную плотность на низких частотах, а при наличии периодических составляющих спектральная плотность имеет максимумы (пики). Основанием для гипотезы о наличии долговременной

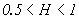памяти является значение коэффициента Херста , который получают в результате 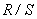анализа [2]. Процедура проверки гипотезы по статистике 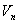подробно описана в [3].

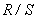Благодаря развитию компьютерных технологий созданы программы, с помощью которых выполняют анализ. Одна из них Fractan 4.4. Эта программа распространяется бесплатно и помещена на многих Internet-сайтах, например, [сылка более недоступна}